NCERT Solutions For Class 10 Maths Chapter 10 Circles Exercise 10.1 - 2025-26
NCERT Solutions For Class 10 Maths Chapter 10 Circles Exercise 10.1 - 2025-26
FAQs on NCERT Solutions For Class 10 Maths Chapter 10 Circles Exercise 10.1 - 2025-26
1. What are the key concepts covered in Class 10 Circles Exercise 10.1?
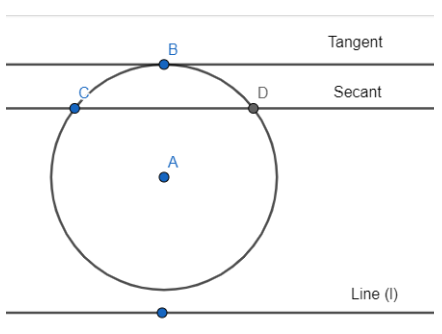
Class 10 Circles Exercise 10.1 focuses on the properties of tangents, chords, and arcs. It includes practical applications and theoretical concepts aligned with the NCERT syllabus.
2. How can I access NCERT Solutions for Class 10 Maths Circles Exercise 10.1?
You can access the NCERT Solutions for Class 10 Maths Circles Exercise 10.1 for free on Vedantu. The solutions include detailed explanations and methodologies for each question.
3. Why are the solutions to Exercise 10.1 important?
The solutions help students understand concepts better, correct common mistakes, and prepare effectively for exams by streamlining their study flow.
4. Can I download a Free PDF of the Class 10 Circles Exercise 10.1 Solutions?
Yes, Vedantu offers a Free PDF of the Class 10 Circles Exercise 10.1 Solutions. This allows for offline access and convenient study.
5. How do NCERT Solutions aid in exam preparation for Class 10 Maths?
NCERT Solutions provide a clear understanding of the chapter, enhance problem-solving skills, and help in self-assessment, ensuring students are well-prepared for exams.
6. What types of questions are included in Exercise 10.1?
Exercise 10.1 includes objective-type questions, multiple-choice questions, and application-based problems related to the properties of circles and tangents.
7. What tools do NCERT Solutions for Exercise 10.1 provide?
NCERT Solutions offer step-by-step methodologies, illustrations, and explanations that help clarify complex concepts and enhance understanding of circles.
8. How can I solve the problems effectively in Circle chapter?
Use NCERT Solutions as a guide to understand each problem. Practice regularly and attempt the exercises to improve your grasp of the Circle chapter.
9. What common mistakes should I avoid in Exercise 10.1?
Common mistakes include miscalculating the radius, confusing tangents with secants, and ignoring the properties of angles related to circles. Use NCERT Solutions to avoid these errors.
10. Are the Class 10 Maths Circles exercises aligned with the latest NCERT guidelines?
Yes, all exercises, including Circles Exercise 10.1, are aligned with the latest NCERT guidelines, ensuring comprehensive coverage of the syllabus.




















 Watch Video
Watch Video