Fast Resolution of Queries with NCERT Exemplar for Class 10 Maths Chapter 9 - Circles (Book Solutions)

Sample Questions

Multiple Choice Questions

Choose the correct answer from the given four options:

1. If angle between two radii of a circle is $130^\circ$, the tangents at the ends of the radii is:

(A) $90^\circ$        

(B) $50^\circ$

(C) $70^\circ$

(D) $40^\circ$

Correct Answer: (B)

Ans: 

$\because$ sum of angles between radii and intersection point of tangent is $180^\circ$

Therefore, 

$\Rightarrow 180^\circ  - 130^\circ  = 50^\circ$

Hence, angle between the tangents at the ends of the radii is $50^\circ$

2. In Fig. 9.1, the pair of Tangents $AP$ and $AQ$ drawn from an external point $A$ to a circle with centre $O$ are perpendicular to each other and length of each tangent is $5cm$. Then the radius of the circle is

(A) $10cm$

(B) $7.5cm$

(C) $5cm$

(D) $2.5cm$

Correct Answer: (C)

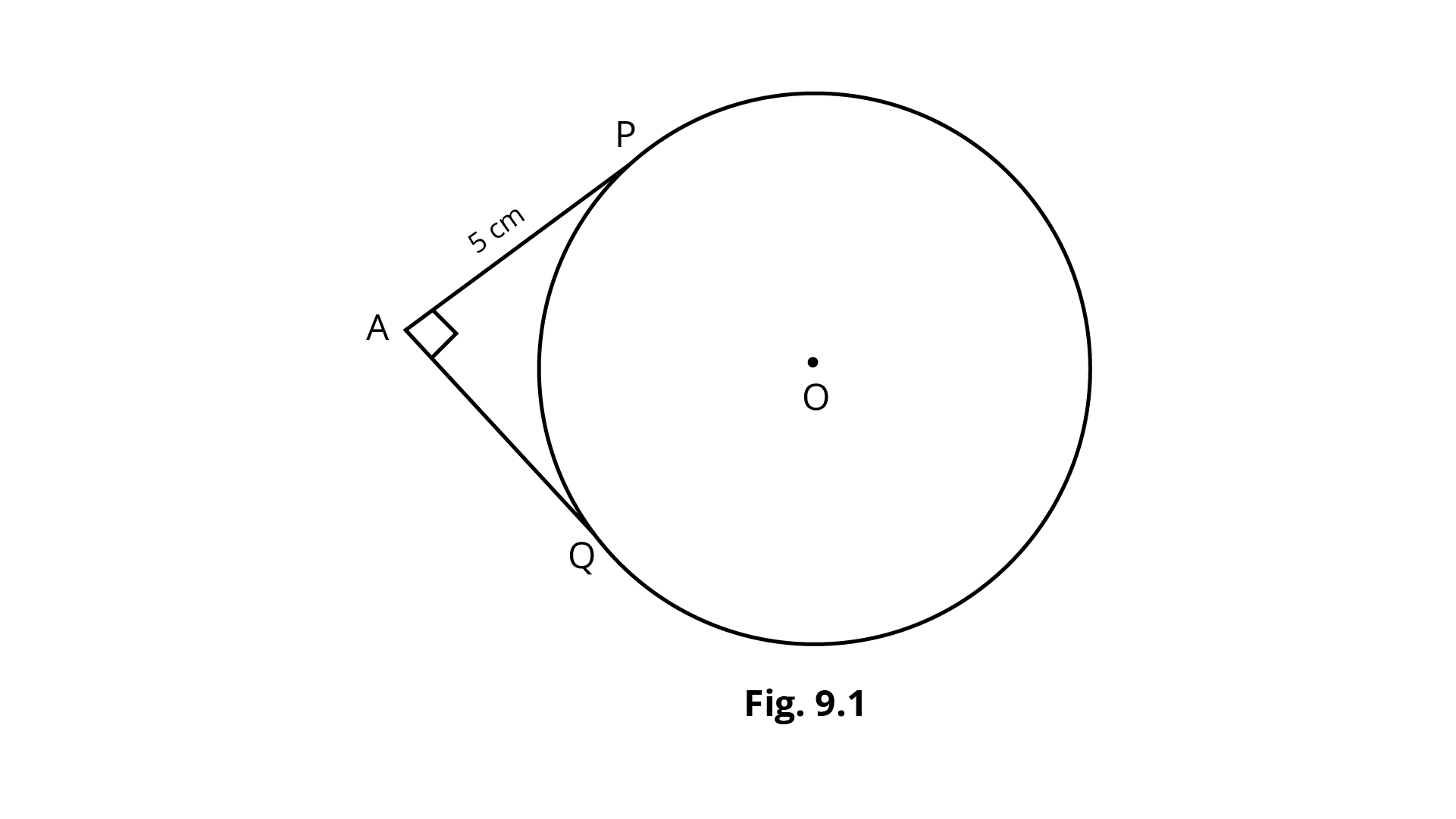
Ans: Given that (${\text{AP}} = {\text{AQ}} = 5{\text{cm}} \because {\text{tangents from external points are equal}}$)

If lines drawn from ${\text{A}}$ to ${\text{O}}$, ${\text{P}}$ to ${\text{O}}$ and ${\text{Q}}$ to ${\text{O}}$ then, radii makes right angle with tangent

So, $\Delta {\text{APO}} \cong \Delta {\text{AQO }}\left( {{\text{by R}}{\text{.H}}{\text{.S}}} \right)$

If, $\angle {\text{PAQ }} = 90^\circ$then $\angle {\text{PAO}} = 45^\circ$

In $\Delta {\text{APO}}$,

${\text{tan45}}^\circ {\text{ = }}\dfrac{{{\text{OP}}}}{{{\text{AP}}}} = \dfrac{{{\text{OP}}}}{5}$

$\therefore 1 = \dfrac{{{\text{OP}}}}{5}$

${\text{OP}} = 5{\text{cm}}$ 

Hence, radii is $5{\text{cm}}$.

3. In Fig. 9.2, $PQ$ is a chord of a circle and $PT$is the tangent at $P$ such that $\angle QPT = 60^\circ$ Then $\angle PRQ$ is equal to

(A) $135^\circ$

(B) $150^\circ$

(C) $120^\circ$

 (D) $110^\circ$

Correct Answer: (C)

$[{\text{Hint }}:\angle {\text{OPQ }} = \angle {\text{OPQ }} = 30^\circ ,{\text{ }}i.e.,\angle {\text{POQ}} = 120^\circ .{\text{Also, }}\angle {\text{PRQ}}{\text{ = }}\dfrac{1}{2}{\text{reflex}}\angle {\text{POQ]}}$

Ans: Because radius and tangent are perpendicular at their point of contact so, $\angle {\text{OPT}} = 90^\circ$

Therefore, 

$\angle {\text{OPQ}} = \angle {\text{OPT}} - \angle {\text{QPT}}$

$\Rightarrow {\text{90}}^\circ  - 60^\circ  = 30^\circ$ 

${\text{OQ}} = {\text{OP}} = {\text{radius}}$

So, $\angle {\text{OPQ}} = \angle {\text{OQP }} = 30^\circ[{\text{angles opposite to equal sides]}}$

In $\Delta {\text{POQ}}$

$\angle {\text{POQ}}{\text{ + }}\angle {\text{OPQ}}{\text{ +  }}\angle {\text{OQP }} = 180^\circ$

$\angle {\text{POQ}} = 180^\circ  - 30^\circ  - 30^\circ  = 120^\circ$

Now, 

$\angle {\text{POQ}}{\text{ +  reflex}}\angle {\text{POQ}} = 360^\circ$

${\text{reflex}}\angle {\text{POQ}} = 360^\circ  - 120^\circ  = 240^\circ$ 

As angle subtended by an arc at the centre doubles the angle subtended.

So, $\angle {\text{PRQ}} = \dfrac{1}{2}({\text{reflex}}\angle {\text{POQ)}} = 120^\circ$

EXERCISE 9.1 

Multiple Choice Questions (MCQs)

1. If radii of two concentric circles are 4 cm and 5 cm, then length of each chord of one circle which is tangent to the other circle, is

(A) $3 cm{\text{}}$
(B) $6 cm{\text{}}$  
(C) $9 cm{\text{}}$
(D) $1 cm{\text{}}$

Ans: B

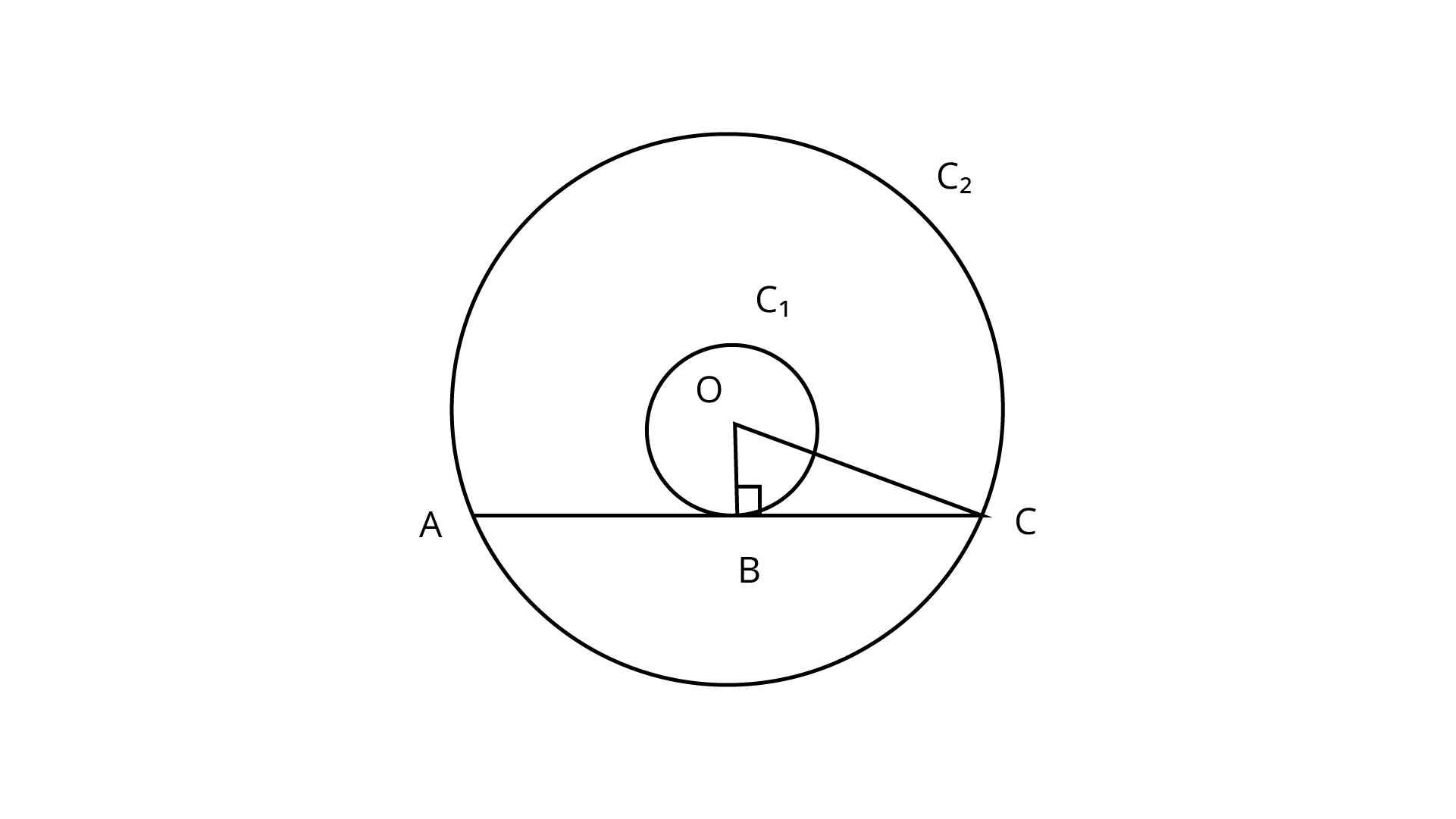
Let O be the centre of two concentric circles${C_1}$  and ${C_2}$, whose radii are ${{\text{r}}_{\text{1}}}{\text{ =  4 cm and }}{{\text{r}}_{\text{2}}}{\text{ =  5 cm}}$ 

Now, we draw a chord AC of circle ${C_2}$, which touches the circle ${C_1}$ at B.

Also, join OB, which is perpendicular to AC. 

(Tangent at any point of circle is perpendicular to radius thoroughly the point of contact)

Now, in right angled $\Delta OBC$, by using Pythagoras theorem,

$O{C^2} = B{C^2} + B{O^2}$  $\because \left[{{({\text{ hypotenuse }})}^2} = {{({\text{ base }})}^2} + {{({\text{ perpendicular })}}^2} \right]$

$\Rightarrow \quad {5^2} = B{C^2} + {4^2}$

$\Rightarrow \quad B{C^2} = 25 - 16 = 9 \Rightarrow BC = 3{\text{cm}}$

$\therefore$ Length of chord $AC  =  2BC  =  2 \times 3  =  6cm$

2. In figure, if $\angle AOB  =  125^\circ$ then $\angle COD$ is equal to

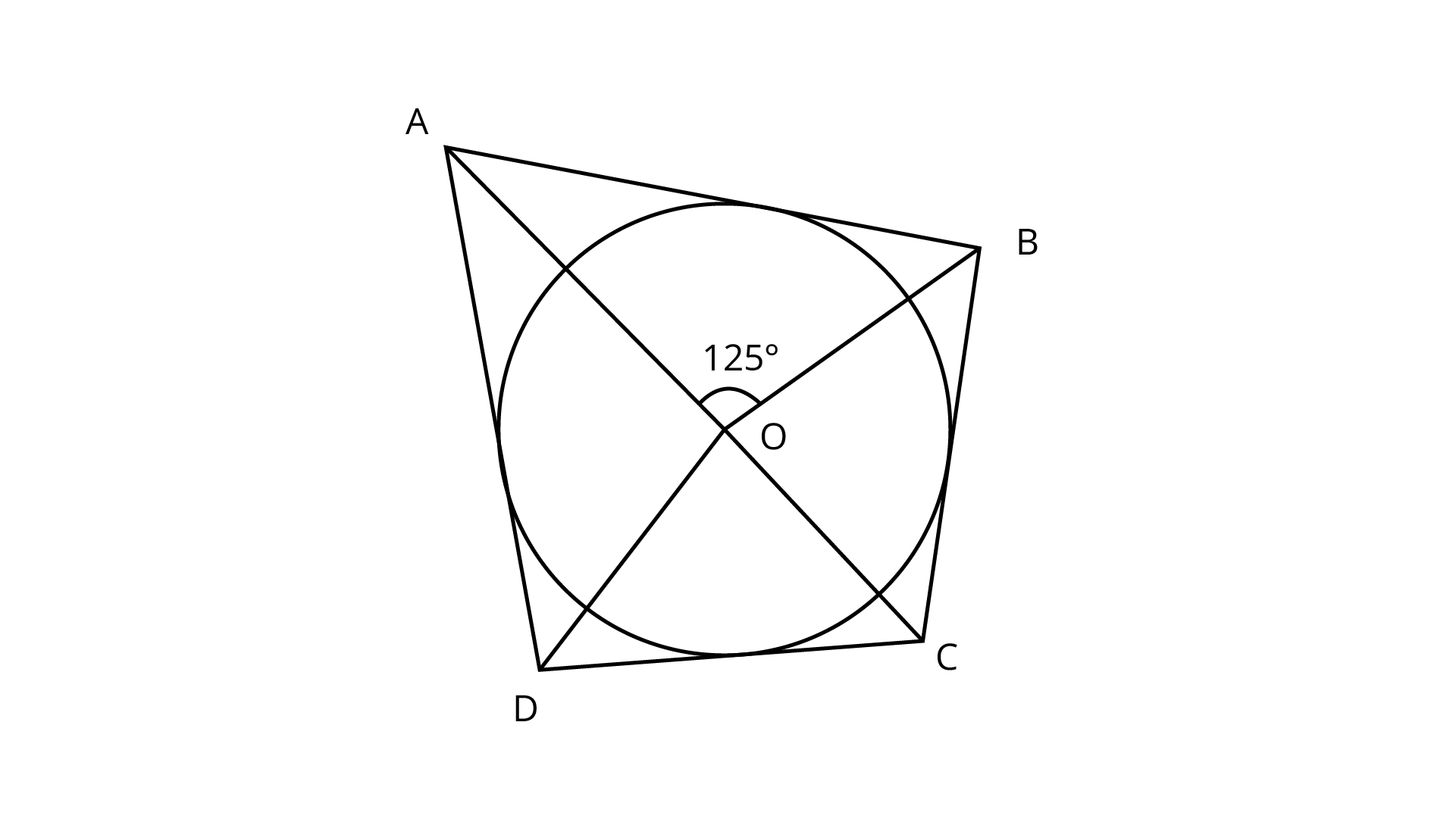
(A) $62.{5^ \circ }$
(B) $4{5^ \circ }$
(C) $3{5^ \circ }$
(D) $5{5^ \circ }$

Ans: D

We know that, the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

i.e., $\angle AOB  + \angle COD  =  18{0^o}$ 

$\Rightarrow \angle COD  =  18{0^o}{\text{ }} - \angle AOB$ 

$\Rightarrow \angle COD  =  18{0^o}  -  12{5^o}$ 

$\Rightarrow \angle COD  =  5{5^o}$ 

3. In figure, AB is a chord of the circle and AOC is its diameter such that $\angle ACB  =  50^\circ$. If AT is the tangent to the circle at the point A, then $\angle BAT$ is equal to

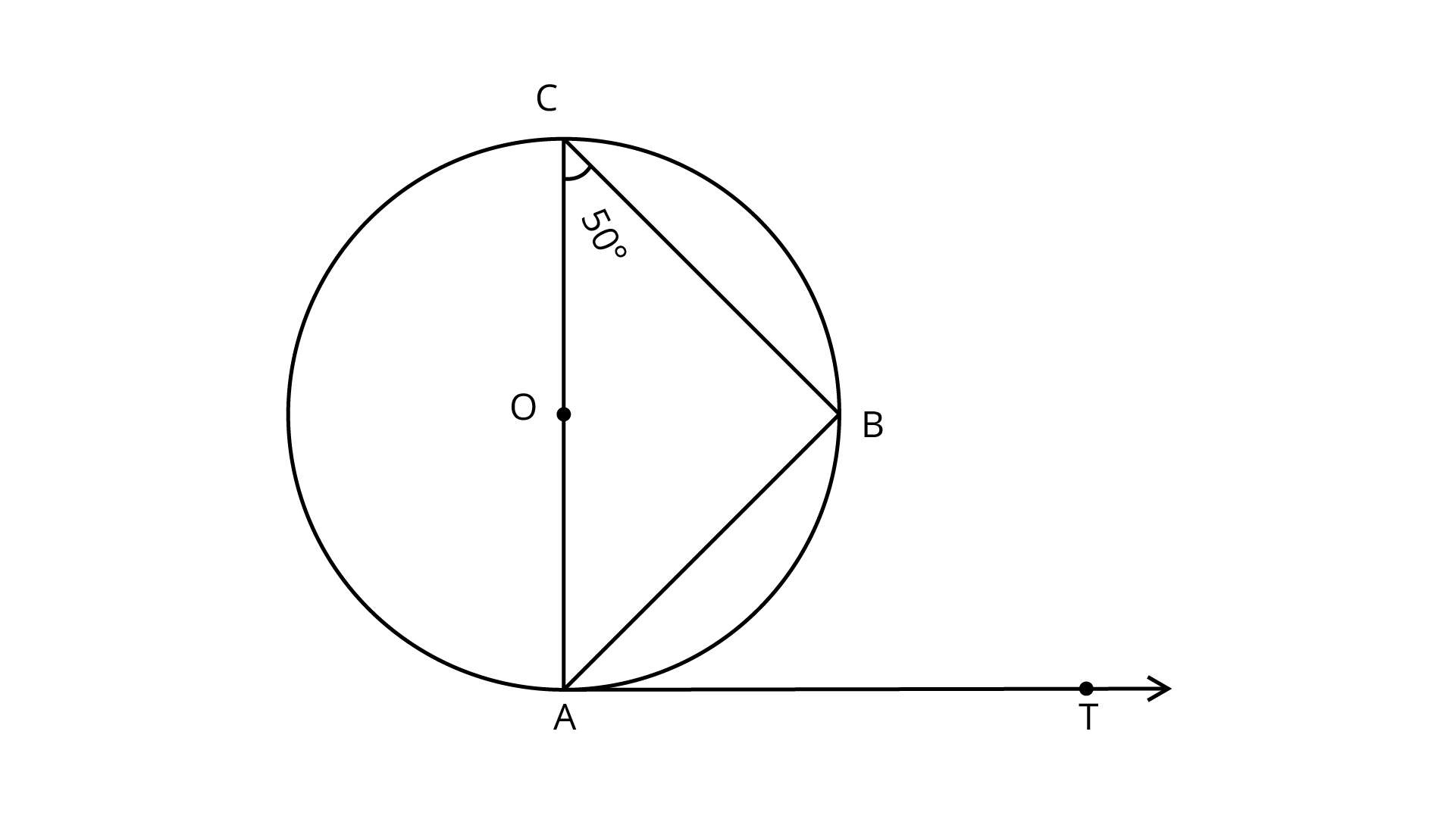
(A) $4{5^\circ }$
(B) $6{0^\circ }$
(C) $5{0^\circ }$
(D) $5{5^\circ }$

Ans: C

In figure, AOC is the diameter of the circle. We know that diameter subtends an angle ${90^\circ }$ at the circle.

So, $\angle ABC = {90^\circ }$

In $\Delta {\text{ACB}}$,

$\angle A + \angle B + \angle C = {180^\circ }$

(Since, sum of all angles of a triangle is ${180^\circ }$)

$\Rightarrow \angle A + {90^\circ } + {50^\circ } = {180^\circ }$

$\Rightarrow  \angle A + 140 = 180$

$\Rightarrow  \angle A = {180^\circ } - {140^\circ } = {40^\circ }$

$\angle A$ or $\angle OAB = {40^\circ }$

Now, AT is the tangent to the circle at point ${\text{A}}$. So, OA is perpendicular to AT.

$\therefore\angle OAT = {90^\circ }$     (from figure)

$\Rightarrow\angle OAB + \angle BAT = {90^\circ }$

On putting $\angle OAB = {40^\circ }$, we get

$\Rightarrow\angle BAT = {90^\circ } - {40^\circ } = {50^\circ }$

Hence, the value of $\angle BAT$ is ${50^\circ }$.

4. From a point P which is at a distance of $13 cm$ from the centre O of a circle of radius $5 cm$, the pair of tangents PQ and PR to the circle is drawn. Then, the area of the quadrilateral PQOR is
(A) $60c{m^2}$
(B) $65 c{m^2}$
(C) $30c{m^2}$
(D) $32.5c{m^2}$

Ans: A

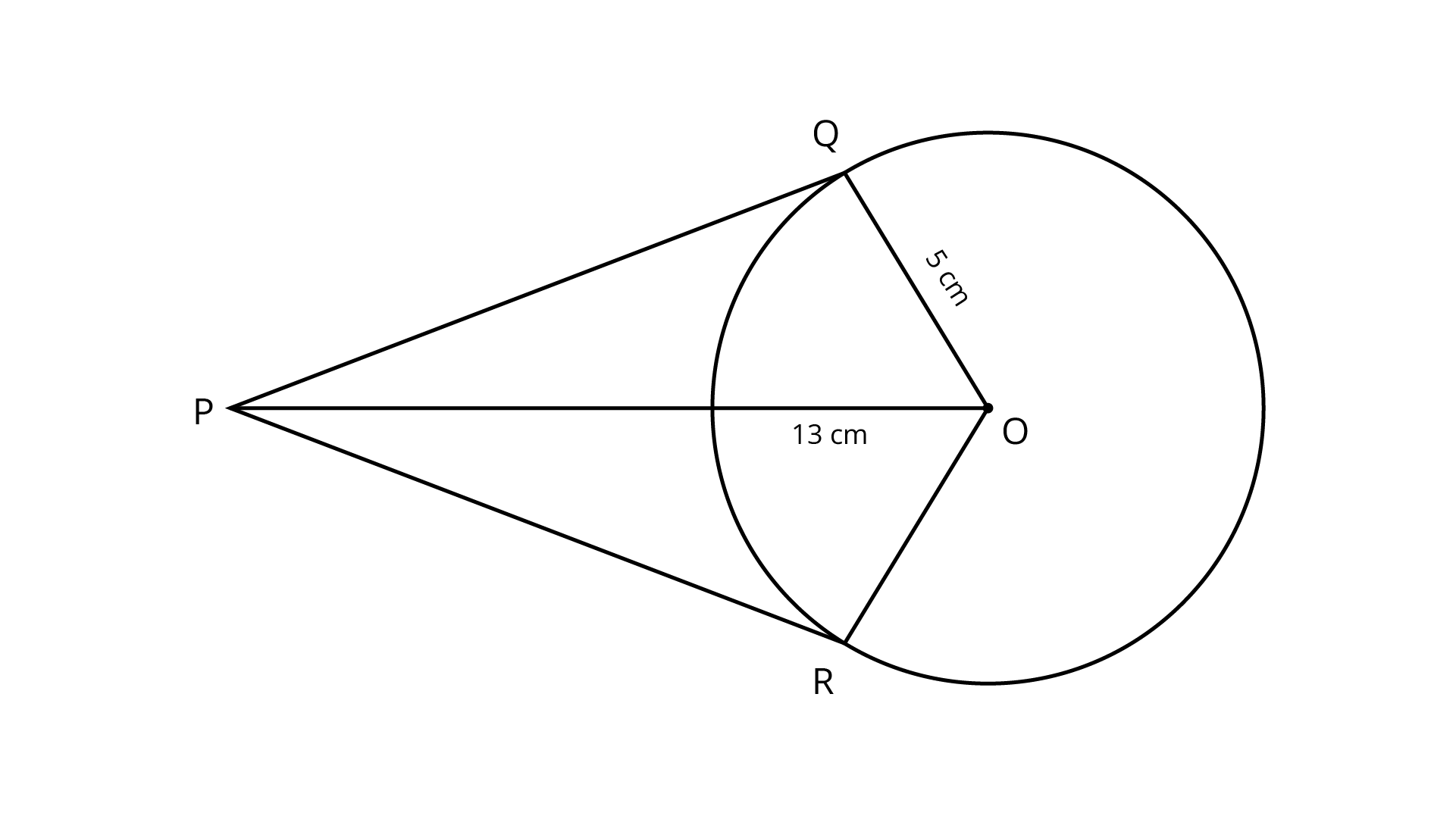
Firstly, draw a circle of radius 5 cm having centre O. 

P is a point at a distance of 13 cm from O. 

A pair of tangents PQ and PR is drawn.

Thus, quadrilateral PQOR is formed.

$\because OQ \bot QP\quad$ (Since, AP is a tangent line)

In right angled $\Delta PQO,\quad O{P^2} = O{Q^2} + Q{P^2}$

$\Rightarrow {13^2} = {5^2} + Q{P^2}$

$\Rightarrow Q{P^2} = 169 - 25 = 144$

$\Rightarrow QP = 12{\text{cm}}$

Now, ${\text{area of }}\Delta OQP{\text{ }} = \dfrac{1}{2} \times QP \times QO{\text{ }}$

$= \dfrac{1}{2} \times 12 \times 5 = 30{\text{c}}{{\text{m}}^2}{\text{ }}$

$\therefore$ Area of quadrilateral ${QORP=2}{{\Delta OQP}} {{=2 \times 30  =  60c}}{{\text{m}}^{\text{2}}}$

5. At one end A of a diameter AB of a circle of radius $5 cm$, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A, is
(A) $4 cm$                             
(B) $5 cm$
(C) $6 cm$
(D) $8 cm$

Ans: D

First, draw a circle of radius ${\text{5 cm}}$ having centre O. 

A tangent XY is drawn at point A.

A chord CD is drawn which is parallel to XY and at a distance of $8{\text{cm}}$ from $A$. 

Now, $\angle OAY = {90^\circ }$

(Tangent at any point of a circle is perpendicular to the radius through the point of contact)

$\Delta OAY + \Delta OED = {180^\circ }$

$\therefore$ sum of co interior is ${180^\circ }$

$\Rightarrow \Delta OED = {180^0}$

Also, $AE = 8{\text{cm}}.\operatorname{Join} OC$

Now, in right angled $\Delta OEC,$

$\Rightarrow O{C^2} = O{E^2} + E{C^2}$ (By Pythagoras theorem)

$\Rightarrow E{C^2} = O{C^2} - O{E^2}\quad $

$= {\text{ }}{{\text{5}}^2}{\text{  -  }}{{\text{3}}^2}$  

$\because OC  =  \text{radius}  =  5 cm, OE  =  AE -- AO  =  8  -  5  =  3 cm$

$= {\text{ 25  -  9}}$ 

$\Rightarrow {\text{EC}}{\text{ = }}{\text{4 cm}}$  

Hence, length of chord $CD = 2CE = 2 \times 4 = 8{\text{cm}}$ 

(Since, perpendicular from centre to the chord bisects the chord)

6. In figure, AT is a tangent to the circle with centre o such that OT  =  4 cm and $\angle OTA  =  30^\circ$ . Then, AT is equal to

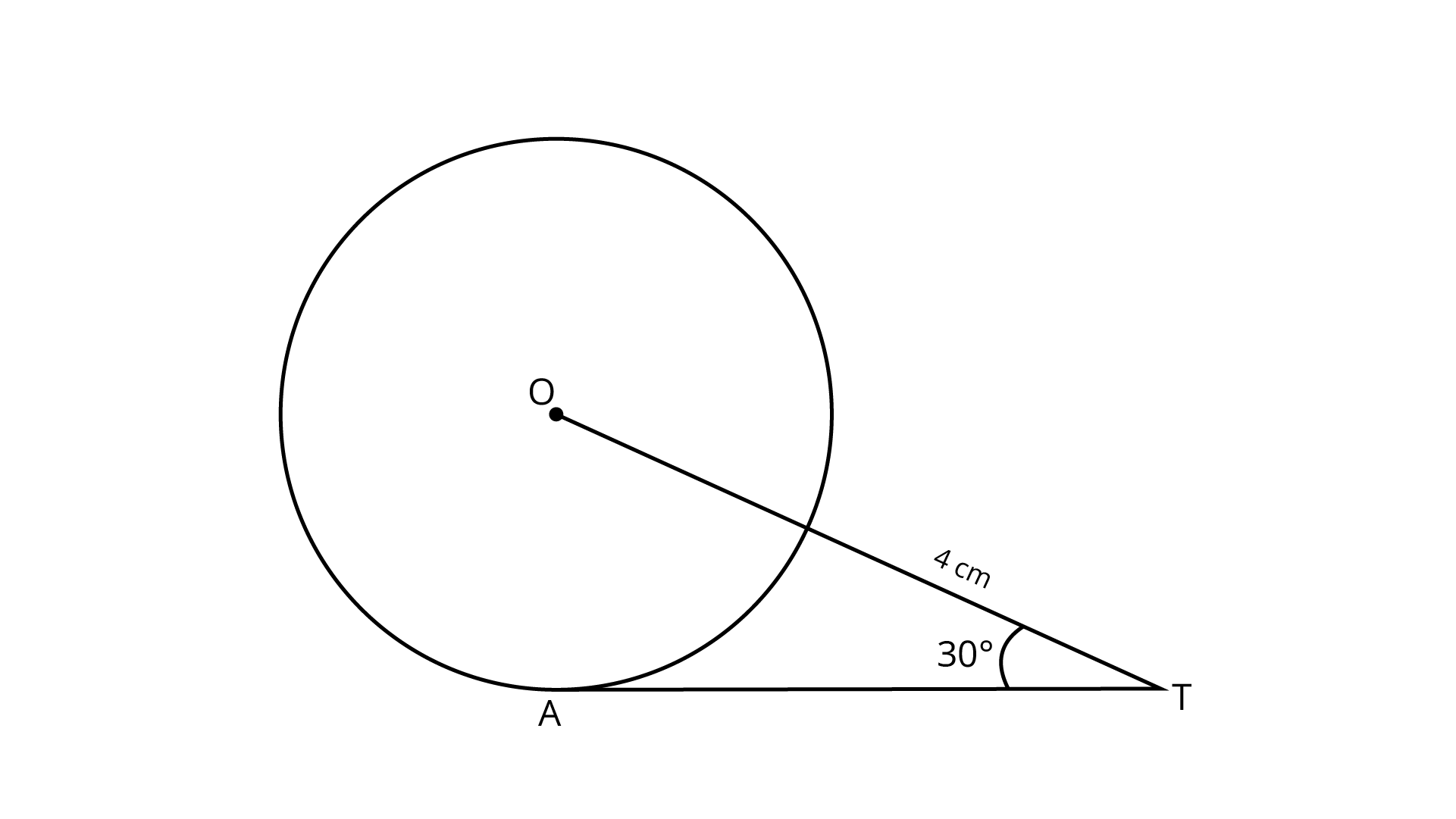
(A) $4 cm{\text{}}$
(B) $2 cm{\text{}}$
(C) $2\sqrt 3  cm{\text{}}$
(D) $4\sqrt 3  cm{\text{}}$

Ans: C

Join OA

We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

$\therefore \angle {\text{OAT  =  9}}{{\text{0}}^0}$ 

${\text{In }}\Delta {\text{OAT, cos 3}}{{\text{0}}^0}{\text{  =  }}\dfrac{{{\text{AT}}}}{{{\text{OT}}}}$ 

$\Rightarrow {\text{ }}\dfrac{{\sqrt 3 }}{2}{\text{  =  }}\dfrac{{{\text{AT}}}}{{\text{2}}}$ 

$\Rightarrow {\text{ AT  =  2}}\sqrt 3 {\text{ cm}}$

7. In figure, if 0 is the centre of a circle, PQ is a chord and the tangent PR at P, makes an angle of $50^\circ$ with PQ, then $\angle POQ$ is equal to

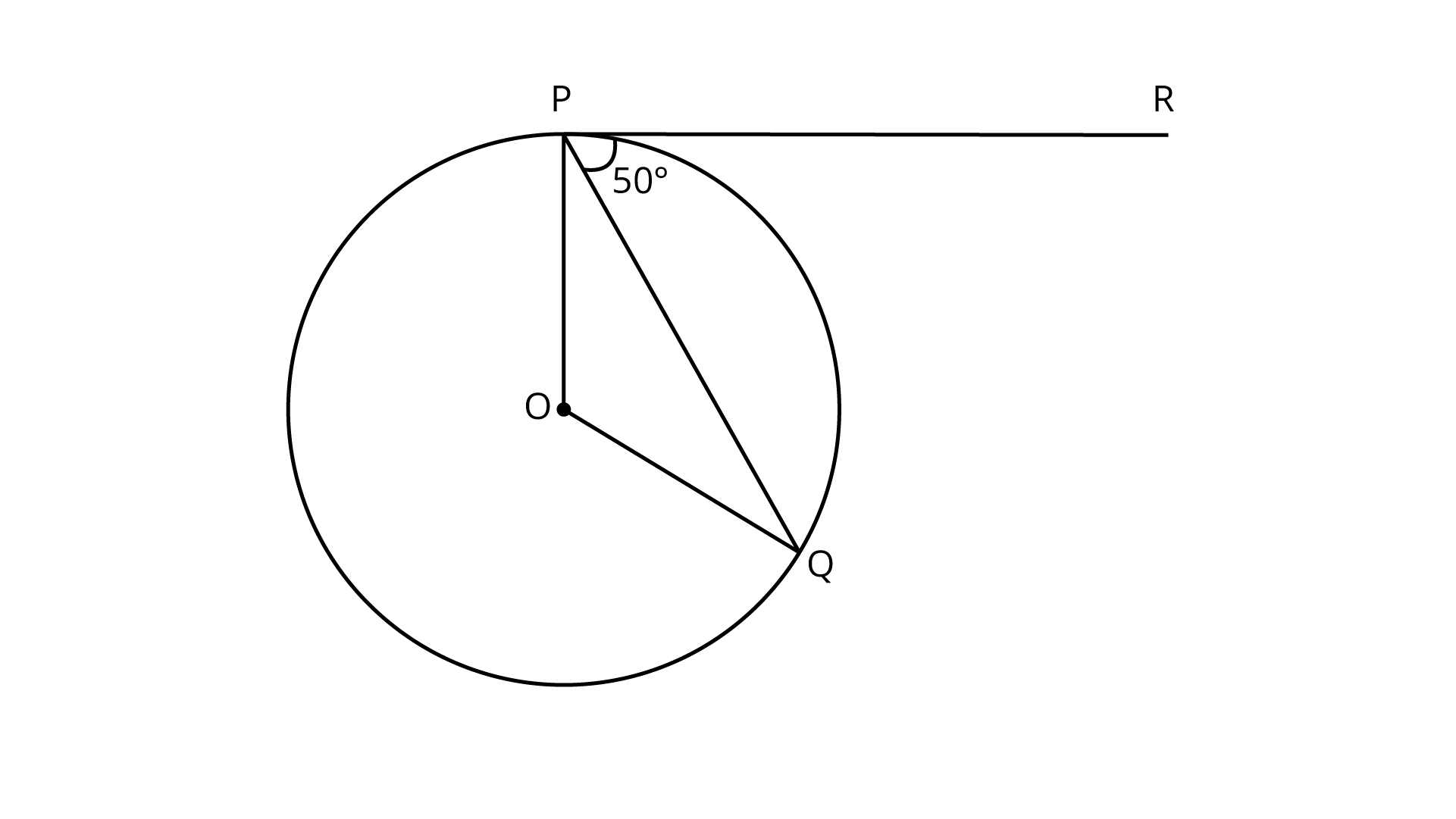
(A) $100^\circ$

(B) $80^\circ$
(C) $90^\circ$
(D) $75^\circ$

Ans: A 

Given, $\angle QPR=5{{0}^\circ}$

We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

$\therefore \angle OPR=9{{0}^{\circ}}$

$\Rightarrow \quad \angle OPQ + \angle QPR = {90^\circ}\quad$ (from figure)

$\angle OPQ =9{{0^\circ}}{\text{-5}}{{0}^{\circ}} = {40^0} \because \angle QPR = {{50}^\circ}$

${\text{Now, OP  =  OQ  =  Radius of circle}}$

$\therefore \angle OQP = \angle OPQ = {40^\circ }$ (Since, angles opposite to equal sides are equal)

In $\Delta OPQ,\quad \angle O + \angle P + \angle Q = {180^\circ }$ (Since, sum of angles of a triangle ${ = {{180}^\circ }}$)

$\Rightarrow \angle O = {180^\circ } - \left( {{{40}^\circ } + {{40}^\circ }} \right)\left[ {\because \angle P = {{40}^\circ } = \angle Q} \right]$

$\Rightarrow {180^\circ } - {80^\circ } = {100^\circ }$ 

8: In figure, if PA and PB are tangents to the circle with centre O such that $\angle APB  =  50^\circ$, then $\angle OAB$ is equal to

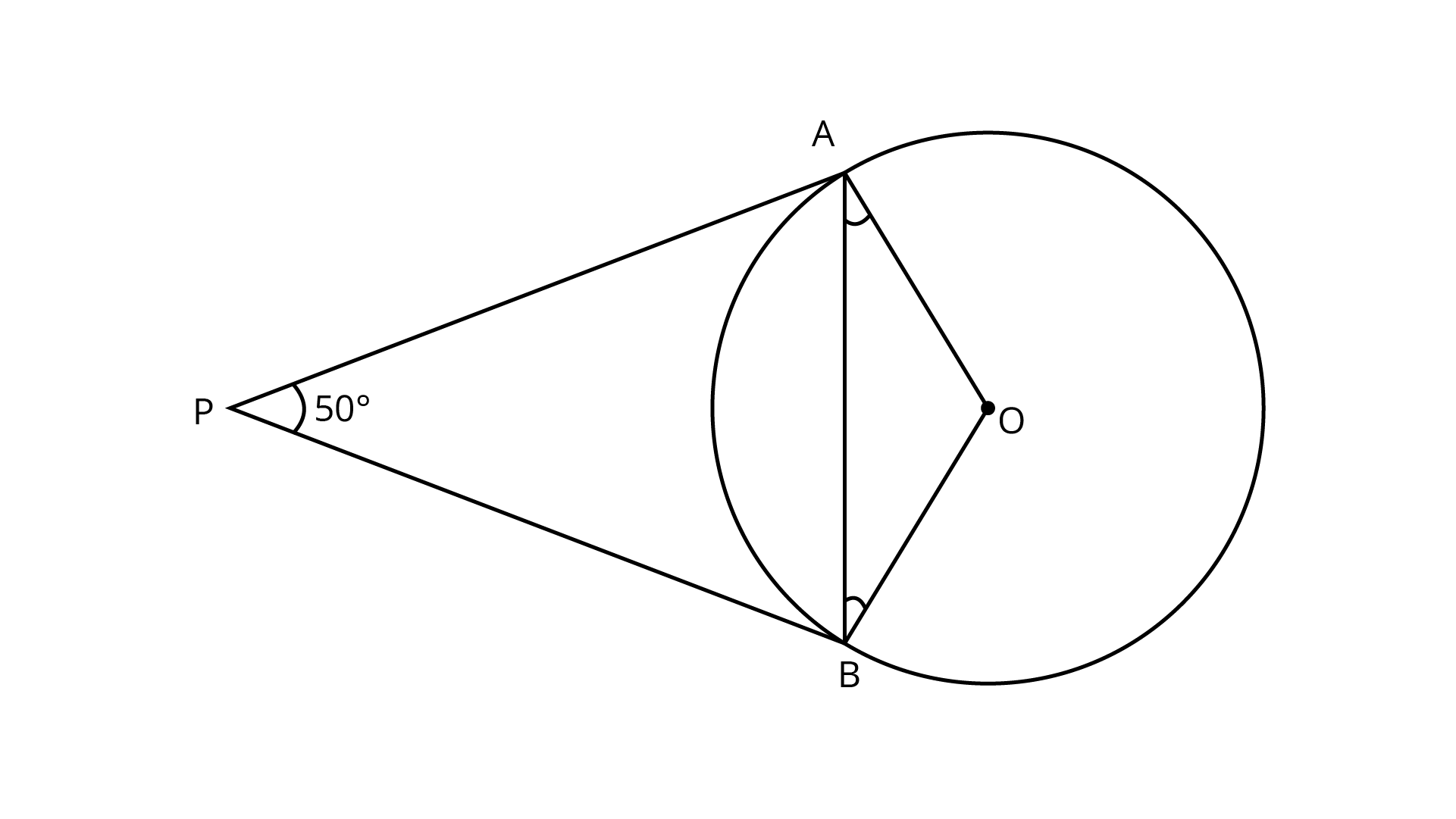
(A) $25^\circ$

(B) $30^\circ$    
(C) $40^\circ$   
(D) $50^\circ$

Ans: A

Given, ${\text{PA}}$ and ${\text{PB}}$ are tangent lines.

$\therefore PA = PB$

(since, the length of tangents drawn from an external point to a circle is equal)

$\Rightarrow \angle PBA = \angle PAB = \theta \quad$ [say]

In $\Delta PAB$, $\angle P + \angle A + \angle B = {180^\circ }$ (since, sum of angles of a triangle $= {180^\circ }$ )

$\Rightarrow {50^\circ } + \theta  + \theta  = {180^\circ }$

$\Rightarrow 2\theta  = {180^\circ } - {50^\circ } = {130^\circ }$

$\Rightarrow \theta  = {65^\circ }$

Also, $OA \bot PA$  (Since, tangent at any point of a circle is perpendicular to the radius through the point of contact)

$\therefore \angle PAO = {90^\circ }$

$\Rightarrow \angle PAB + \angle BAO = {90^\circ }$

$\Rightarrow \quad {65^\circ } + \angle BAO = {90^\circ }$

$\Rightarrow \quad \angle BAO = {90^\circ } - {65^\circ } = {25^\circ }$

Given, PA and PB are tangent lines.

9. If two tangents inclined at an angle $60^\circ$ are drawn to a circle of radius $3 cm$, then the length of each tangent is
(A) $\dfrac{3}{2}\sqrt 3  cm$
(B) $6 cm$
(C) $3 cm$
(D) $3\sqrt 3  cm$

 Ans: D

Let P be an external point and a pair of tangents is drawn from point P and the angle between these two tangents is $60^\circ$.

Join OA and OP

Also, OP is a bisector line of $\angle {\text{APC}}$ 

$\therefore \angle {\text{APO  =  }}\angle {\text{CPO  =  3}}{{\text{0}}^0}$ 

Also, ${\text{OA}} \bot {\text{ AP}}$ (Tangent at any point of a circle is perpendicular to the radius through the point of contact).

${\text{In }}\Delta {\text{OAP, tan 3}}{{\text{0}}^0}{\text{  =  }}\dfrac{{{\text{OA}}}}{{AP}}$ 

$\Rightarrow {\text{ }}\dfrac{1}{{\sqrt 3 }}{\text{  =  }}\dfrac{3}{{{\text{AP}}}}$ 

$\Rightarrow {\text{ AP  =  3}}\sqrt 3 {\text{ cm}}$ 

Hence, the length of each tangent is ${\text{ 3}}\sqrt 3 {\text{ cm}}$

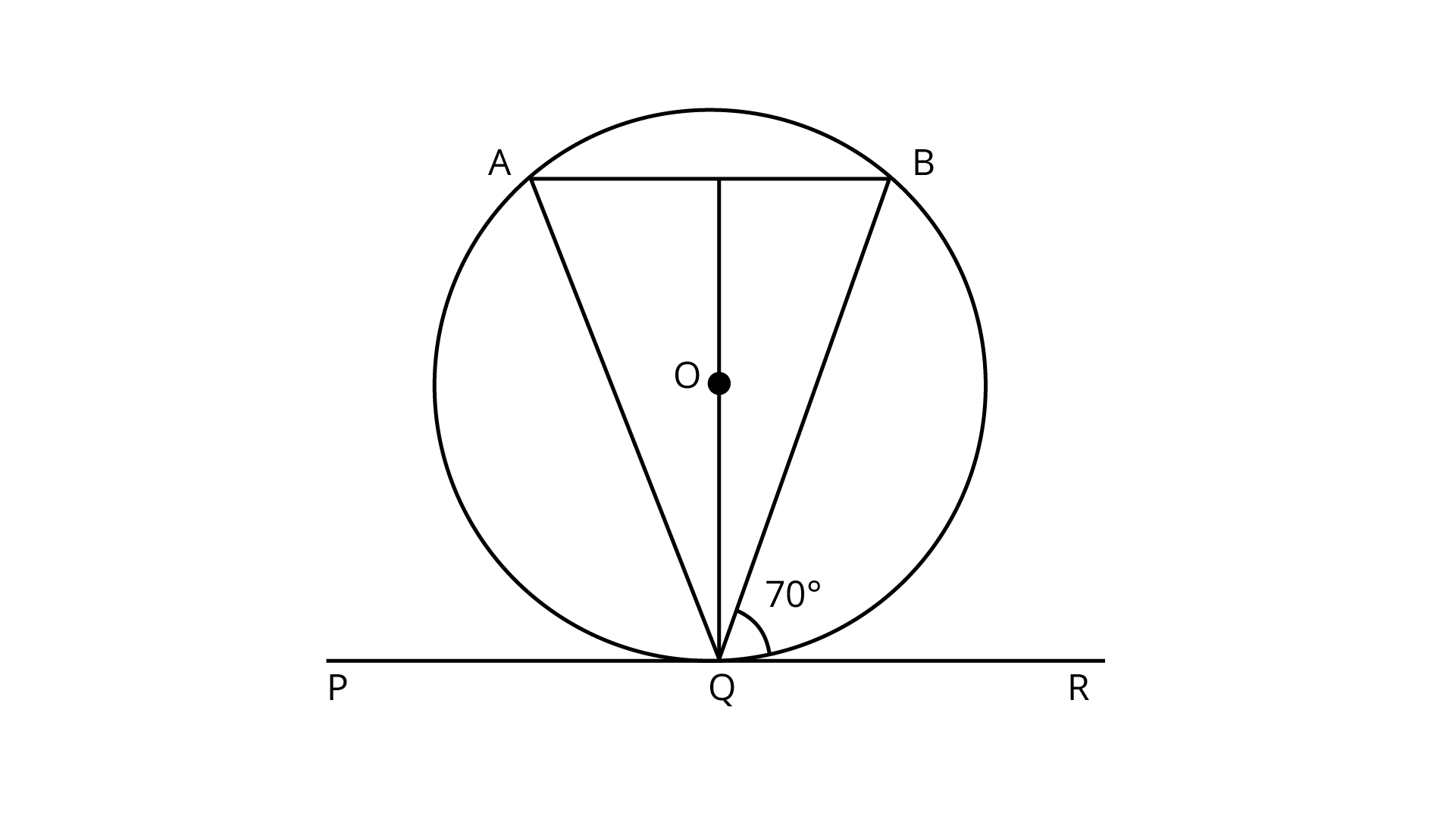
10. In figure, if PQR is the tangent to a circle at Q whose centre is 0, AB is a chord parallel to PR and $\angle BQR  =  70^\circ$ , then $\angle AQB$ is equal to

(A) $20^\circ$
(B) $40^\circ$               
(C) $35^\circ$                   
(D) $45^\circ$

Ans: B

Given AB ║PR

$\therefore \angle ABQ = \angle BQR = {70^\circ }$   (Alternate angles)

Also, QD is perpendicular to AB and QD bisects AB. 

In $\Delta QDA$ and $\Delta QDB$,

$\angle QDA = \angle QDB$        (each 90⁰)

$AD = BD$

$QD = QD$  (common side)

$\therefore \Delta ADQ \cong \Delta BDQ$  (By SAS similarity criterion)

Then $\angle QAD = \angle QBD[{\text{CPCT}}] \ldots ({\text{i}})$ 

Also, $\angle ABQ = \angle BQR$ (alternate interior angle)

$\therefore \angle ABQ = {70^\circ }$   $\left[ {\because \angle BQR = {{70}^\circ }} \right]$ 

Hence, $\angle QAB = {70^\circ }$   (from Eq. (i))

Now, In $\vartriangle {\text{ABQ}}$ 

$\angle A + \angle B + \angle Q = {180^\circ }$

$\Rightarrow \angle Q = {180^\circ } - \left( {{{70}^\circ } + {{70}^\circ }} \right) = {40^\circ }$

SAMPLE QUESTIONS

Write ‘True’ or ‘False’ and give reasons for your answer.

1. In Fig. $9.9$, $BOA$ is the diameter of a circle and the tangent at a point $P$ meets $BA$ extended at $T$. If $\angle PBO = 3{0^o}$, then $\angle PTA$ is equal to $3{0^o}$?

Ans: True. 

As $\angle BPA  =  90^\circ ,$

$\angle PAB  = \angle OPA  =  60^\circ$

Also, $OP \bot PT.$

Therefore, $\angle APT  =  30^\circ \text{ and }\angle PTA  =  60^\circ - 30^\circ  =  30^\circ .$ 

2. In Fig. $9.10$, $PQL$ and $PRM$ are tangents to the circle with centre $O$ at the points $Q$ and $R$, respectively and $S$ is a point on the circle such that $\angle SQL = 5{0^o}$ and  $\angle SRM = 6{0^o}$. Then $\angle QSR$ is equal to $4{0^o}$.

Ans: False.

Given that $\angle SQL = {50^ \circ }$,

$\Rightarrow \angle OSQ = {90^ \circ } - {50^ \circ } = {40^ \circ }$

As the angles opposite to equal sides are equal,

$\Rightarrow \angle OSQ = \angle OQS = {40^ \circ }$.

And $\angle SRM = {60^ \circ }$,

$\Rightarrow \angle RSO = {90^ \circ } - {60^ \circ } = {30^ \circ }$

As the angles opposite to equal sides are equal,

$\Rightarrow \angle RSO = \angle SRO = {30^ \circ }$.

So, $\angle QSR = {40^ \circ } + {30^ \circ } = {70^ \circ }$. 

Hence, $\angle QSR = {70^ \circ }$.

EXERCISE 9.2

Very Short Answer Type Questions

1. If a chord AB subtends an angle of $60^\circ$ at the centre of a circle, then the angle between the tangents at A and B is also $60^\circ$.

Ans: False

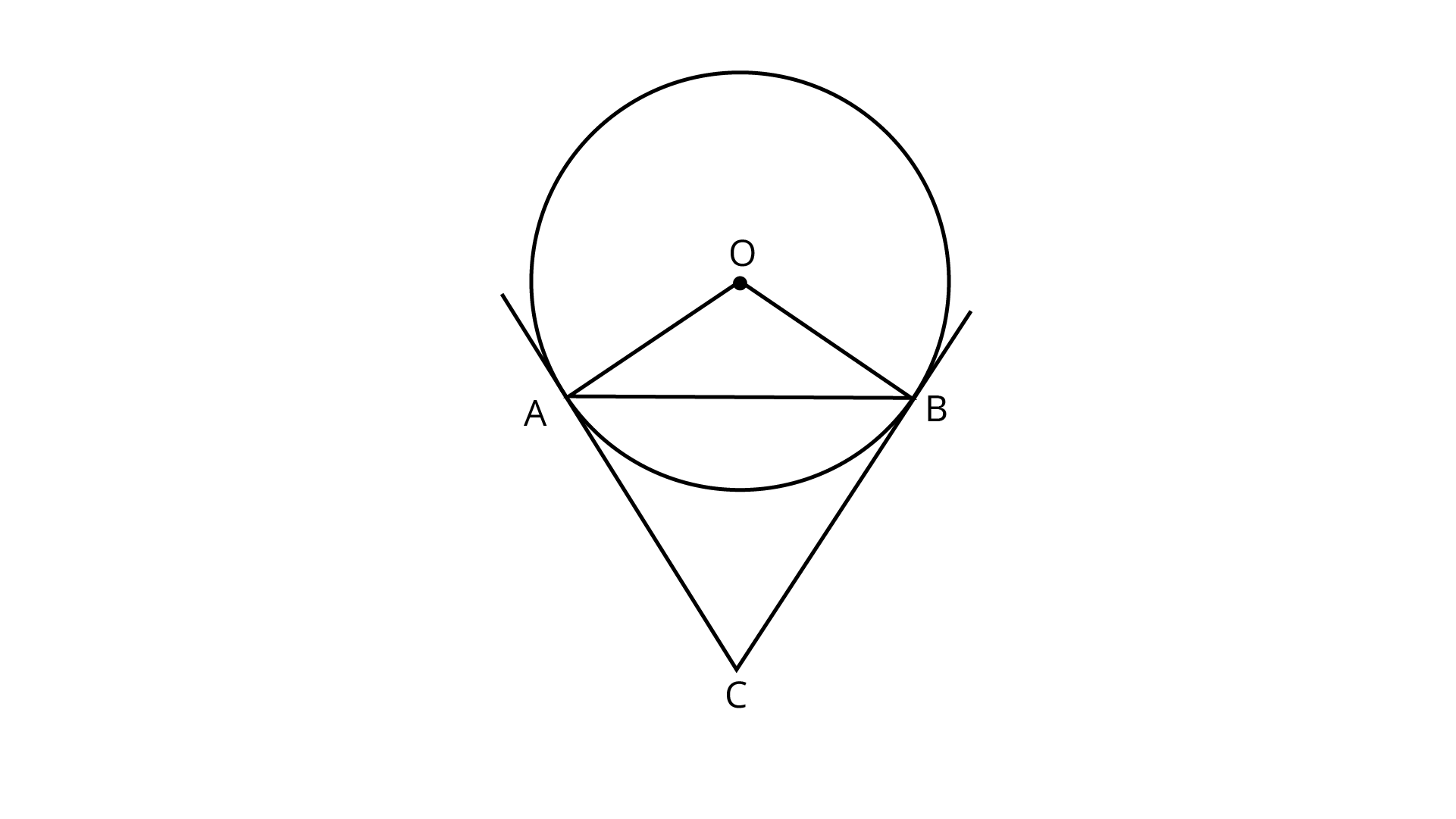
Since a chord AB subtends an angle of $60^\circ$  at the centre of a circle.

i.e., $\angle AOB = {60^\circ }$

As $OA = OB =$ Radius of the circle

$\therefore \angle OAB = \angle OBA = {60^\circ }$

The tangent at points $A$ and $B$ is drawn, which intersect at $C$. We know, $OA \bot AC$ and $OB \bot BC$.

$\therefore \angle OAC = {90^\circ },\angle OBC = {90^\circ }$

$\Rightarrow \angle OAB + \angle BAC = {90^\circ }$

And $\angle OBA + \angle ABC = {90^\circ }$

$\Rightarrow \angle BAC = {90^\circ } - {60^\circ } = {30^\circ }$

And $\angle ABC = {90^\circ } - {60^\circ } = {30^\circ }$

In $\Delta {\text{ABC}}$,

$\Rightarrow \angle BAC + \angle CBA + \angle ACB = {180^\circ }$ (Since, sum of all interior angles of a triangle is ${180^\circ }$)

$\Rightarrow \angle ACB = {180^\circ } - \left( {{{30}^\circ } + {{30}^\circ }} \right) = {120^\circ }$

2. The length of tangent from an external point P on a circle is always greater than the radius of the circle.

Ans: False

Because the length of tangent from an external point P on a circle may or may not be greater than the radius of the circle.

3.The length of tangent from an external point P on a circle with centre O is always less than OP.

Ans: True

PT is a tangent drawn from an external point$P$. Join OT.

$\because OT \bot PT$

So, OPT is a right angled triangle formed. 

In a right angled triangle, the hypotenuse is always greater than any of the two sides of the triangle.

$\therefore OP > PT$

Or $PT < OP$

4. The angle between two tangents to a circle may be $0^\circ$.

Ans: True

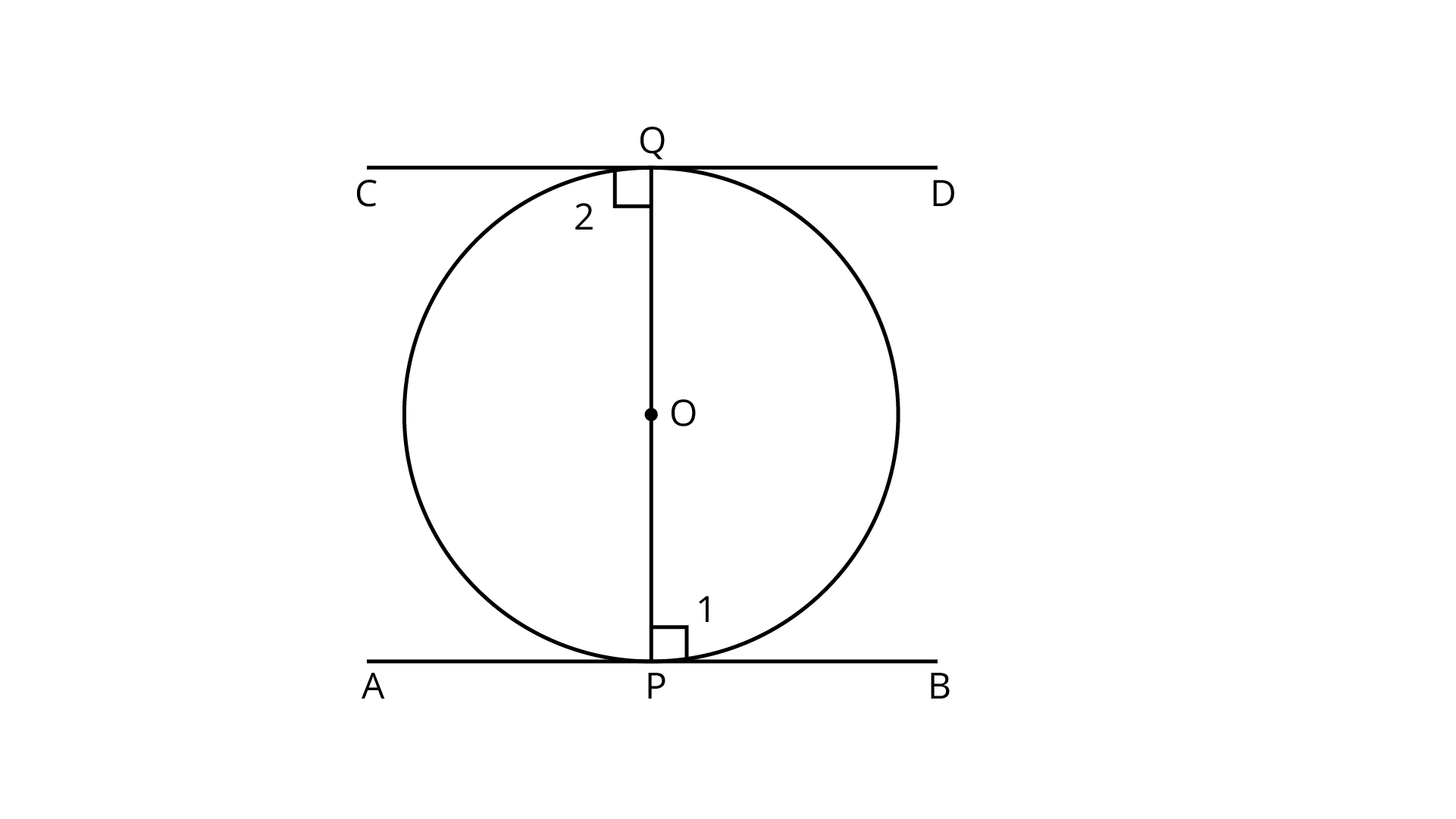
This may be possible only when both tangent lines coincide or are parallel to each other.

5. If angle between two tangents drawn from a point P to a circle of radius a and centre 0 is $90^\circ$ , then $OP = a\sqrt 2$ .

Ans: True

From point ${\text{P}}$, two tangents are drawn. 

Given, OT=a

Also, line OP bisects the $\angle {\text{RPT}}$.

$\therefore \angle TPO = \angle RPO =4{5^\circ}$

Also, ${\text{OT}} \bot {\text{PT}}$

In right angled $\Delta OTP,\quad sin4{5^\circ } = \dfrac{{OT}}{{OP}}$

$\Rightarrow \quad \dfrac{1}{{\sqrt 2 }} = \dfrac{a}{{OP}}$ 

$\Rightarrow OP = a\sqrt 2$

6. If the angle between two tangents drawn from a point P to a circle of radius a and centre O is $60^\circ$ , then $OP  =  2a$.

Ans: True 

From point ${\text{P}}$, two tangents are drawn.

Given, ${\text{OT  =  as}}$

Also, line OP bisects the $\angle {\text{RPT}}$.

$\therefore \angle TPO = \angle RPO = {30^\circ }$

Also, $OT \bot PT$

In right angled $\Delta OTP$,

$\sin {30^\circ } = \dfrac{{OT}}{{OP}}$

$\Rightarrow \dfrac{{\text{1}}}{{\text{2}}}{\text{ = }}\dfrac{{\text{a}}}{{{\text{OP}}}}$

$\Rightarrow {\text{OP  =  2a}}$

7. The tangent to the circumcircle of an isosceles $\Delta ABC$ at A, in which $AB = AC$, is parallel to BC.

Ans: True

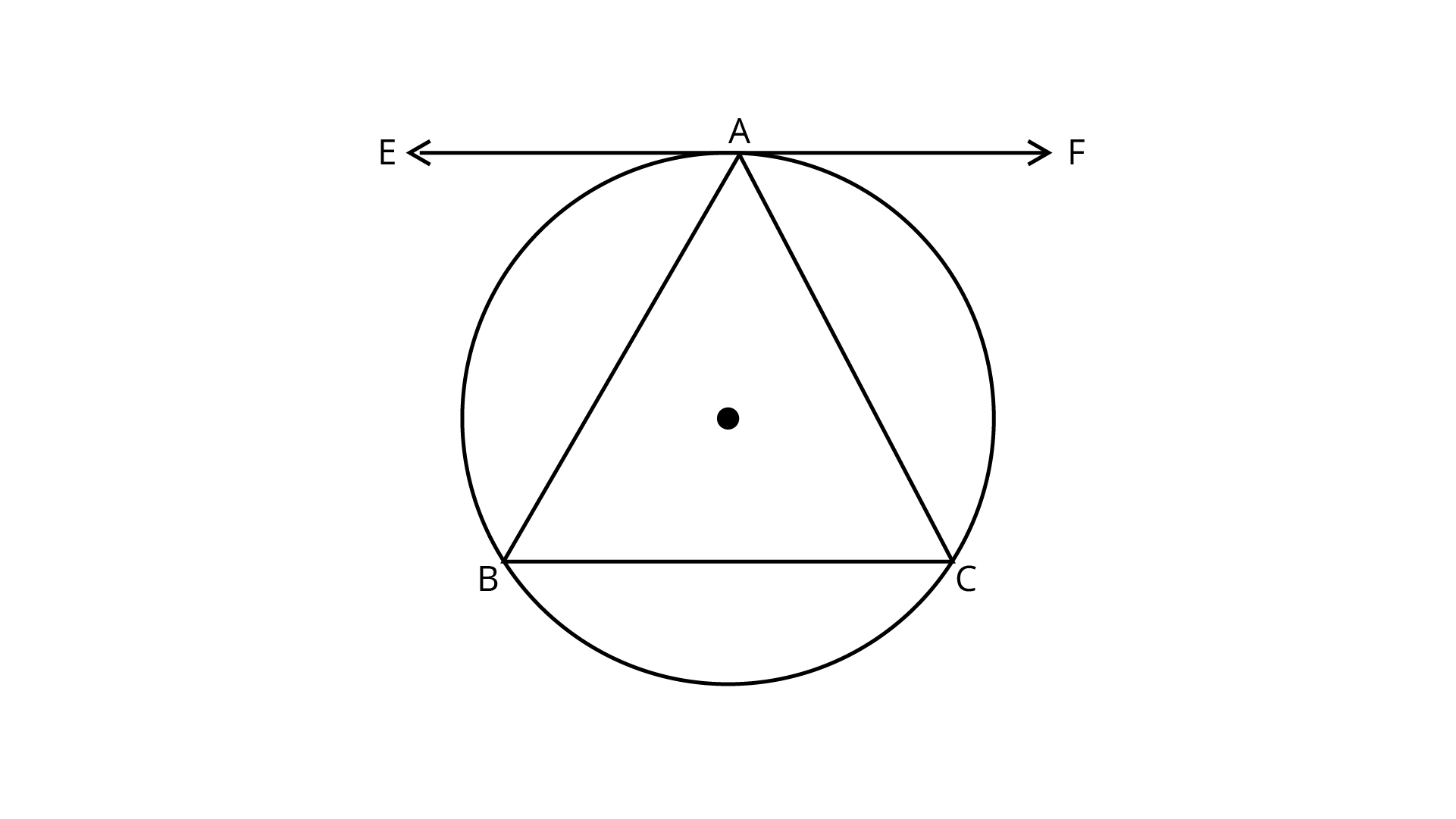
Let EAF be tangent to the circumcircle of $\Delta ABC$ .

Here, $AB = AC$

$\Rightarrow \angle {\text{ABC  =  }}\angle {\text{ACB}}$... (i)

(Angle between tangent and is chord equal to angle made by chord in the alternate segment)

$\therefore$ Also, $\angle {\text{EAB  =  }}\angle {\text{BCA}}$... (ii)

From Eqs. (i) And (ii), we get 

$\Rightarrow \angle EAB = \angle ABC$

$\Rightarrow EAF{\text{ }}||{\text{ }}BC$
  

8. If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.

Ans: False

Given that PQ is any line segment and ${S_1}, {S_2}, {\text{ }}{S_3}, {\text{ }}{S_4}$ … circles are touch a line segment PQ at a point A. Let the centres of the circles${S_1}, {S_2}, {\text{ }}{S_3}, {\text{ }}{S_4}$… be ${C_1}, {C_2}, {\text{ }}{C_3}, {\text{ }}{C_4}$ … respectively.

To prove centres of these circles lie on the perpendicular bisector PQ

Now, joining each centre of the circles to the point A on the line segment PQ by a line segment i.e.,  ${C_1}A, {\text{ }}{C_2}A, {\text{ }}{C_3}A, {\text{ }}{C_4}A$ … so on.

We know that, if we draw a line from the centre of a circle to its tangent line, then the line is always perpendicular to the tangent line. But it does not bisect the line segment PQ.

${C_1}A \bot PQ\left[ {{\text{for }}{{\text{S}}_{\text{1}}}} \right]$

 ${C_2}A \bot PQ\left[ {{\text{for }}{{\text{S}}_2}} \right]$

${C_3}A \bot PQ\left[ {{\text{for }}{{\text{S}}_3}} \right]$

${C_4}A \bot PQ\left[ {{\text{for }}{{\text{S}}_4}} \right]$

$ \ldots $ So on.

Since, each circle is passing through a point A. Therefore, all the line segments
${C_1}A,{\text{ }}{C_2}A,{\text{ }}{C_3}A,{\text{ }}{C_4}A$ …. So they are coincidental.

So, centre of each circle lies on the perpendicular line of PQ but they do not lie on the perpendicular bisector of PQ.

Hence, a number of circles touch a given line segment PQ at a point A, then their centres lie

9. If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.

Ans: True

We draw two circles with centres ${C_1}$ and ${C_2}$ passing through the end points $P$ and $Q$ of a line segment PQ. We know that perpendicular bisectors of a chord of a circle always pass through the centre of the circle. 

Thus, the perpendicular bisector of PQ passes through ${C_1}$ and ${C_2}$. Similarly, all the circles passing through P will have their centre on perpendicular bisectors of PQ.

10. AB is the diameter of a circle and AC is its chord such that $\angle BAC  =  30^\circ$ . If the tangent at C intersects AB extended at D, then $BC  =  BD$.

Ans: True

Join BC and OC. 

Given, $\angle BAC = {30^\circ }$

$\Rightarrow \angle BCD = {30^\circ }$  

(Angle between tangent and chord is equal to angle made by chord in the alternate segment)

$\therefore \angle \mathrm{ACD}=\angle \mathrm{ACO}+\angle \mathrm{OCD}=30^{\circ}+90^{\circ}=120^{\circ}$

${\therefore OC \bot CD}$ And $OA = OC =$ radius

$\Rightarrow \angle OAC = \angle OCA = {{30}^\circ }$

In $\vartriangle ACD$

$\angle CAD + \angle ACD + \angle ADC = {180^\circ }$

(Since, sum of all interior angles of a triangle is ${180^\circ }$)

$\Rightarrow {30^\circ } + {120^\circ } + \angle ADC = {180^\circ }$

$\Rightarrow \angle ADC = {180^\circ } - \left( {{{30}^\circ } + {{120}^\circ }} \right) = {30^\circ }$
Now, in $\Delta BCD$
$\angle BCD = \angle BDC = {30^\circ }$

$\Rightarrow BC = BD$

(Since, sides opposite to equal angles are equal)

SAMPLE QUESTIONS

1. If ${d_1}, {d_2}({d_2} > {d_1})$ be the diameters of two concentric circles and $c$ be the length of a chord of a circle which is tangent to the other circle, prove that ${d_2}^2 = {c^2} + {d_1}^2$.

Ans: Let $AB$ be a chord of a circle that touches another circle at $C$.

Now, $\Delta OCB$ is a right-angled triangle.

Using the Pythagoras theorem, 

$\Rightarrow O{C^2} + C{B^2} = O{B^2}$

$\Rightarrow \dfrac{1}{2}{d_1}^2 + \dfrac{1}{2}{c^2} = \dfrac{1}{2}{d_2}^2$

$\Rightarrow {d_2}^2 = {c^2} + {d_1}^2$

Hence proved.

2. If $a, b, c$ are the sides of a right triangle where $c$is the hypotenuse, prove that the radius $r$ of the circle which touches the sides of the triangle is given by $r = \dfrac{{a + b - c}}{2}$.

Ans: 

Let circle touch sides ${\text{BC, CA, AB}}$ of the right angled triangle $ABC$ at ${\text{D, E, F}}$ respectively, where ${\text{BC}} = a{\text{, CA}} = b{\text{, AB}} = c$.

So, ${\text{AE  =  AF and BD  =  BF}}{\text{.}}$

Also, ${\text{CE  =  CD  =  }}r{\text{.}}$

i.e. $b - r = {\text{AF, }}a - r = {\text{BF}}$

or ${\text{AB}} = c = {\text{AF + BF}}$

$\Rightarrow {\text{AB}} = b - r + a - r$

$\Rightarrow r = \dfrac{{a + b - c}}{2}$

Hence proved.

EXERCISE 9.3 

Short Answer Type Questions

1. Out of the two concentric circles, the radius of the outer circle is $5 cm$ and the chord AC of length $8 cm$ is a tangent to the inner circle. Find the radius of the inner circle.

Ans: Let ${C_{{\text{1}}}}{\text{and }}{C_2}$ be the two circles having same centre O. AC is a chord which touches the ${C_1}$ at point D.

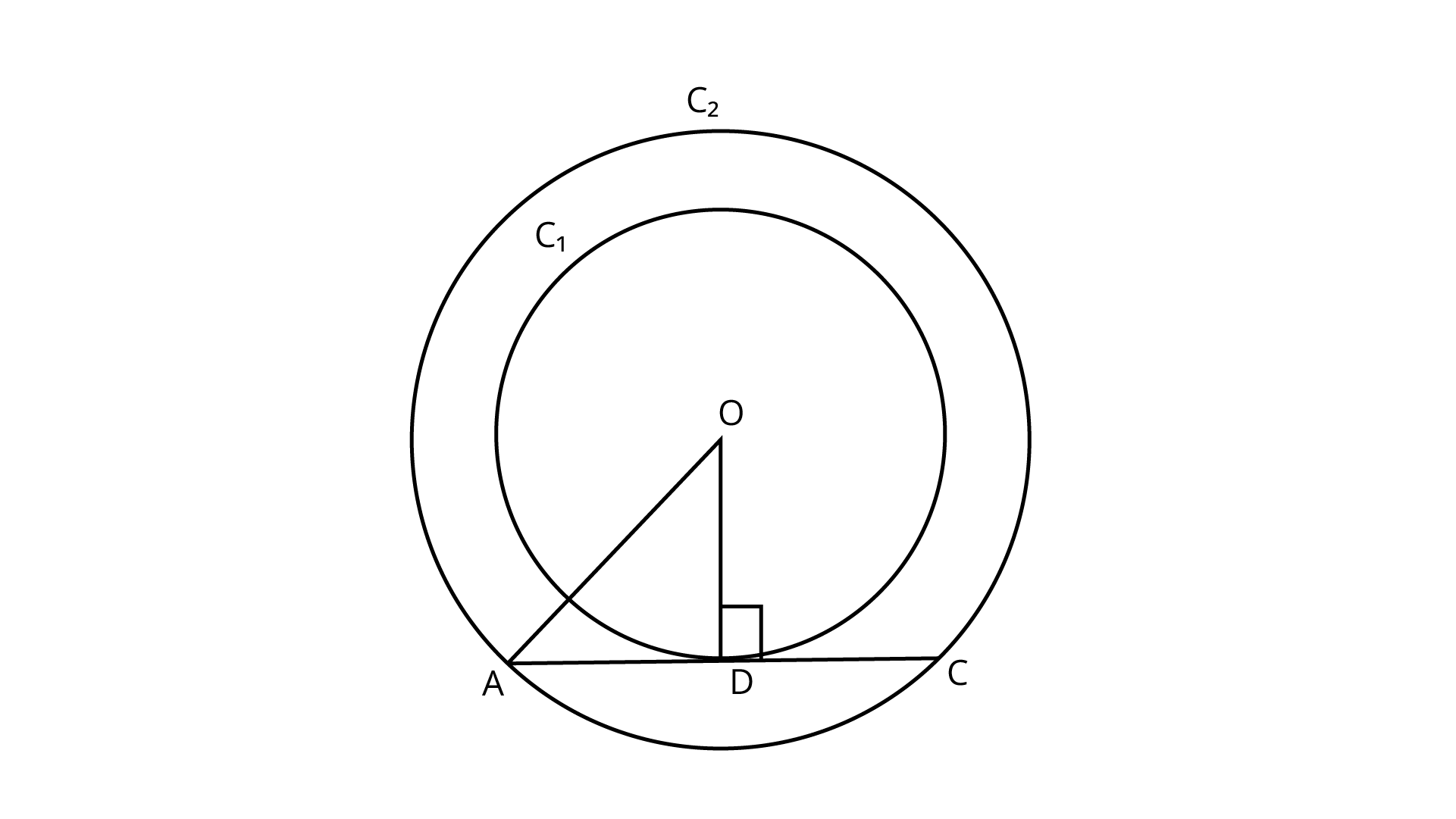
Join OD. 

Also, $OD \bot AC$

$\therefore{\text{AD  =  DC  =  4cm}}\quad$ (Perpendicular line OD bisects the chord)

In right angled $\Delta AOD,$

${\text{O}}{{\text{A}}^{\text{2}}}{\text{  =  A}}{{\text{D}}^{\text{2}}}{\text{ +  D}}{{\text{O}}^{\text{2}}}$

By Pythagoras theorem, i.e.$\left[{\left( {{\text{hypotenuse}}} \right)^2}{\text{ =  ( base }}{{\text{)}}^{\text{2}}}{\text{ +  ( perpendicular }}{{\text{)}}^{\text{2}}}\right]$

$\Rightarrow D{O^2} = {5^2} - {4^2}$

$= 25 - 16 = 9$

$\Rightarrow DO = 3{\text{cm}}$

$\therefore$ Radius of the inner circle ${\text{OD  =  3cm}}$

2. Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.

Ans:

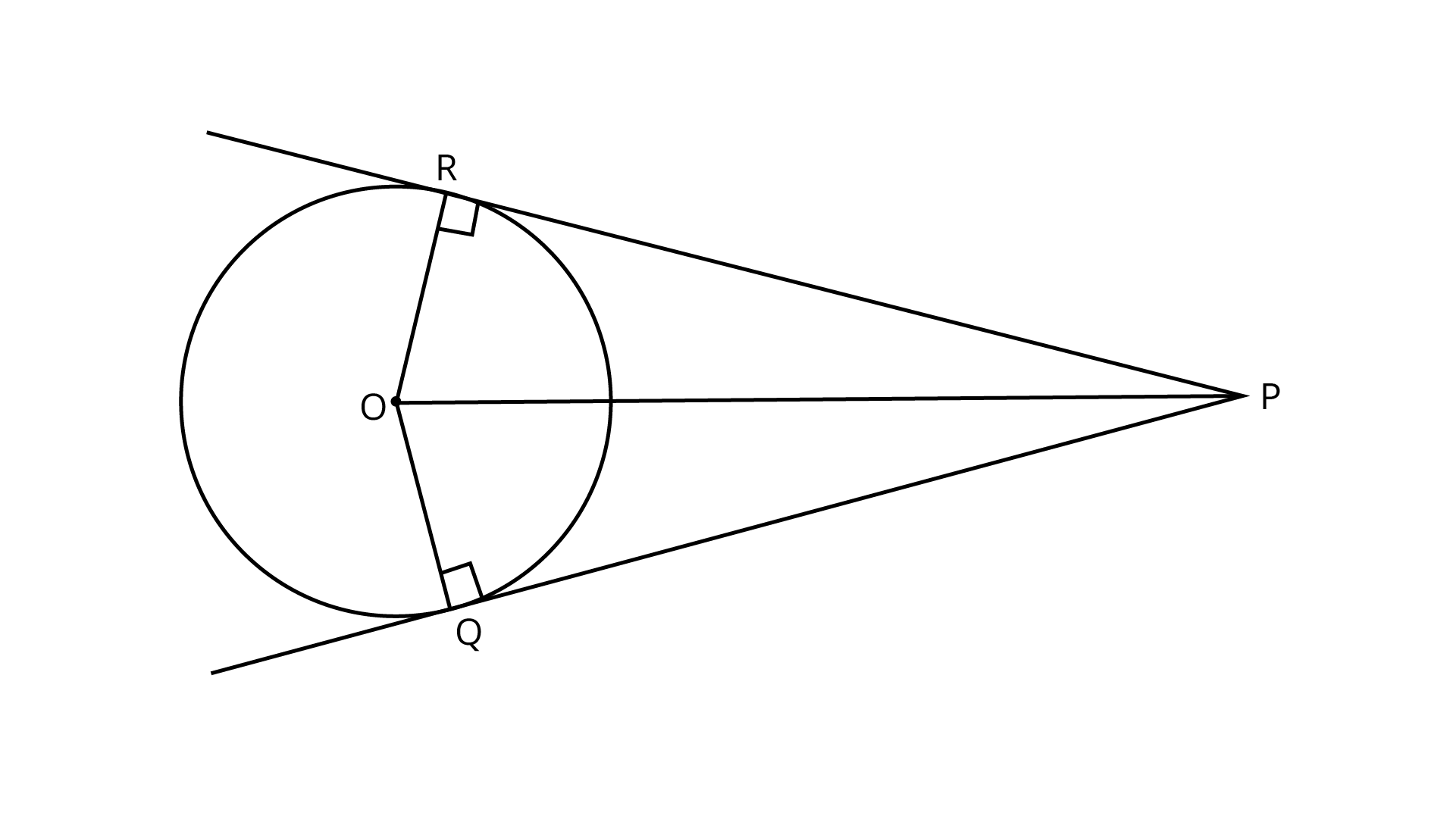
Given: Two tangents PQ and PR are drawn from an external point to a circle with centre O.

Proof: Since, PR and PQ are tangents.

So, $OR \bot PR$ and $OQ \bot PQ$

(Since, if we draw a line from the centre of a circle to its tangent line. Then, the line always perpendicular to the tangent line)

$\therefore \angle ORP = \angle OQP = {90^\circ }$

Hence, $\angle ORP + \angle OQP = {180^\circ }$

So, QOPR is cyclic quadrilateral. 

(If sum of opposite angles is quadrilateral in${180^\circ }$, then the quadrilateral is cyclic)

Hence proved.

3. Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.

Ans:

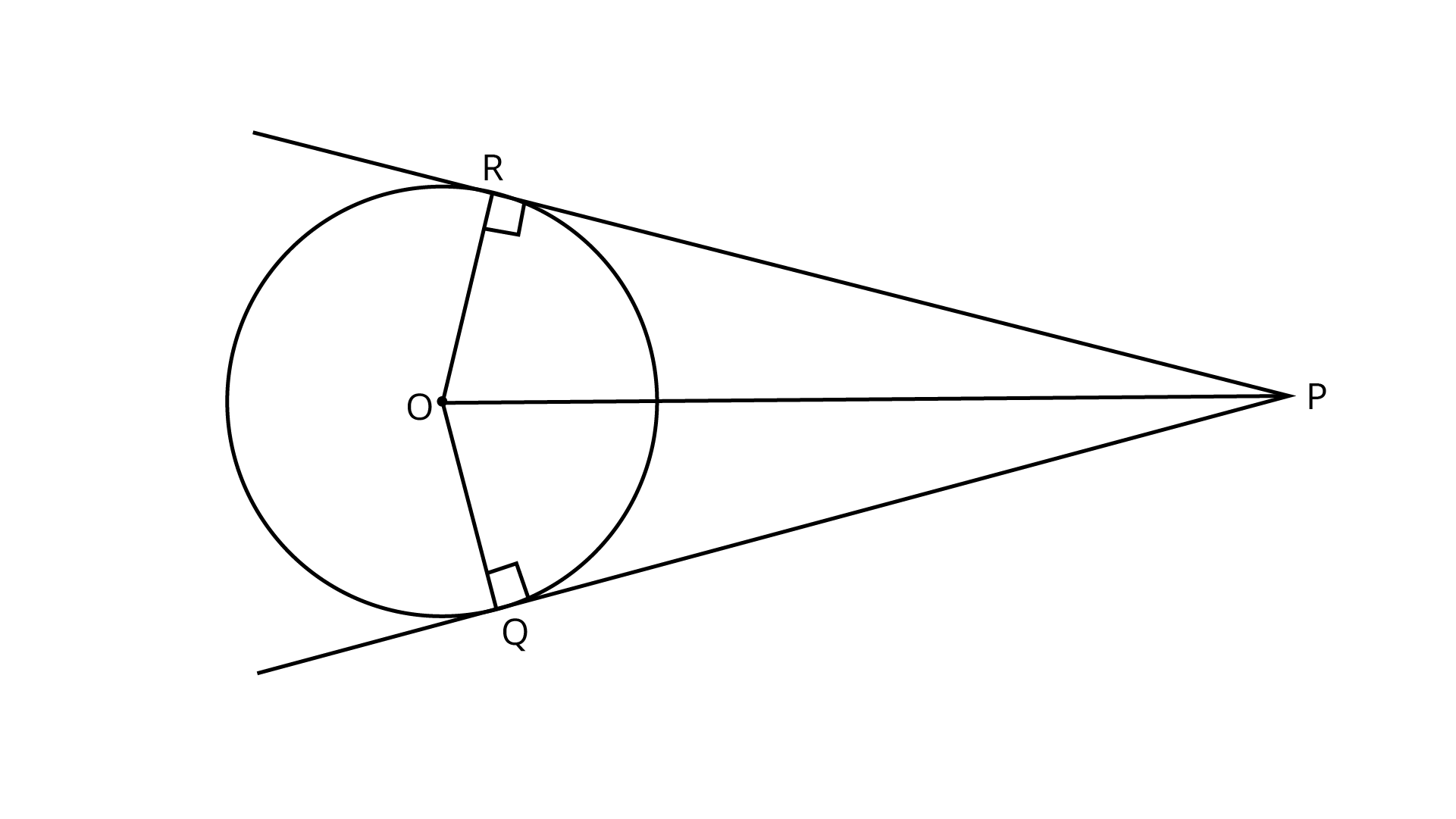
Given: Two tangents PQ and PR are drawn from an external point P to a circle with centre O.
Construction: Join OR, and OQ.

In $\Delta POP{\text{ and }}\Delta PQO$ 

$\angle {\text{PRO  =  }}\angle {\text{PQO  =  9}}{{\text{0}}^ \circ }$ 

(Tangent at any point of a circle is perpendicular to the radius through the point of contact)

$OR{\text{ }} = {\text{ }}OQ$  (Radii of some circle)

Since OP is common

$\therefore \Delta {\text{PRO }} \cong \Delta {\text{PQO}}$ (By RHS)

Hence,$\angle {\text{RPO  =  }}\angle {\text{QPO}}$ (By CPCT)

Thus, O lies on the angle bisector of PR and PQ.     

Hence proved.

4. If from an external point B of a circle with centre $O$, two tangents BC and BD are drawn such that $\angle DBC  =  120^\circ$ , prove that $BC  +  BD  =  BO$ i.e. $BO  =  2 BC$ .

Ans:

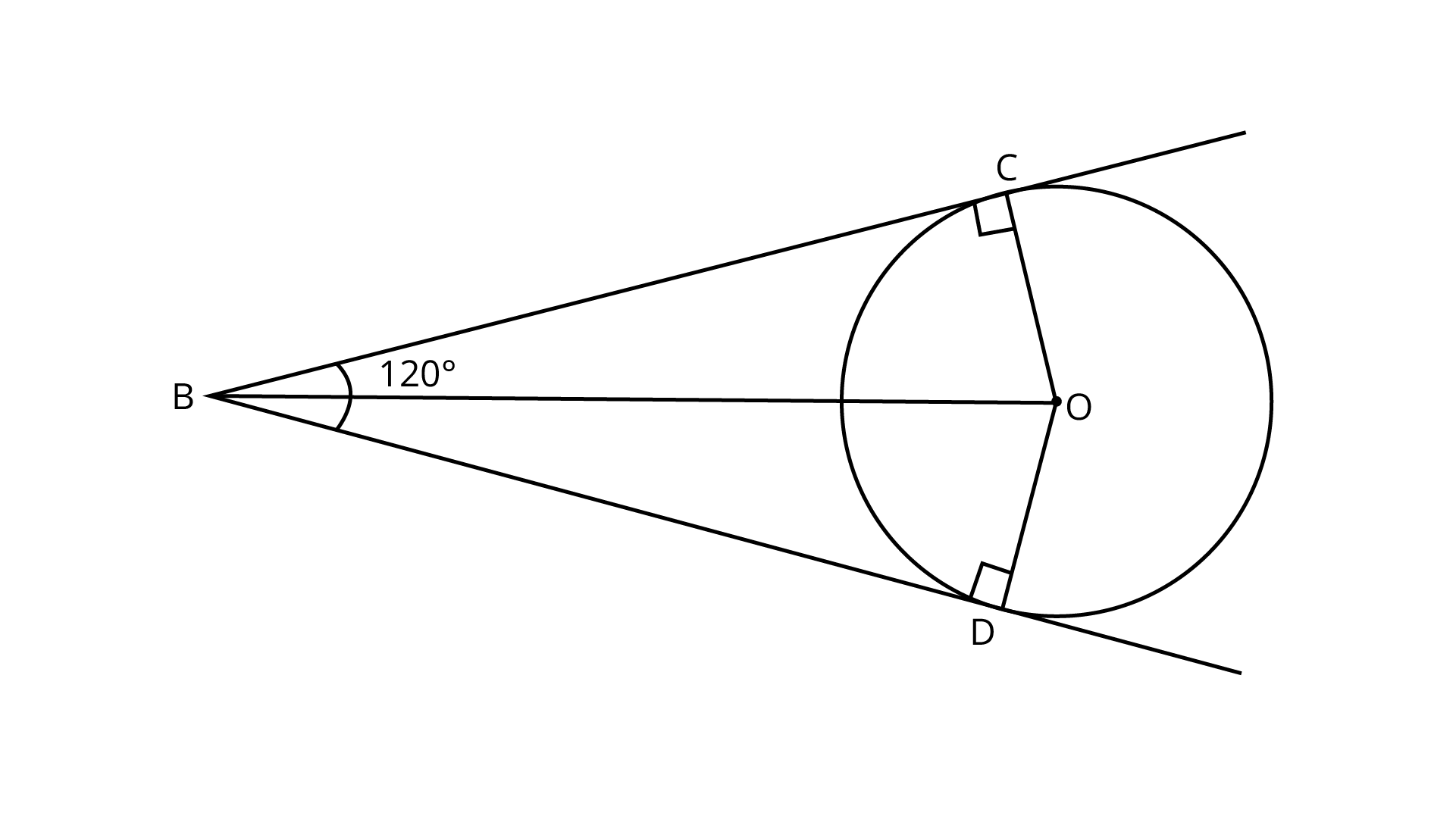
Two tangents BD and BC are drawn from an external point B.

To prove ${\text{BO  =  2BC}}$

Given, $\angle DBC  =  120^\circ$

Join OC, OD and BO. 

Since, BC and BD are tangents.

$\therefore OC \bot BC$ And $OD \bot BD$

We know, OB is an angle bisector of$\angle DBC$.

$\therefore \angle OBC = \angle DBO = {60^\circ }$

In right angled$\Delta {\text{OBC}}$, 

$\cos {60^\circ } = \dfrac{{BC}}{{OB}}$

$\Rightarrow \dfrac{1}{2} = \dfrac{{BC}}{{OB}}$

$\Rightarrow {\text{OB}} = 2{\text{BC}}$

Also, $BC = BD$

(Tangent drawn from internal point to circle are equal)

$\therefore OB = BC + BC$

$\Rightarrow OB = BC + BD$

5. In figure, AB and CD are common tangents to two circles of unequal radii. Prove that $AB  =  CD$ 

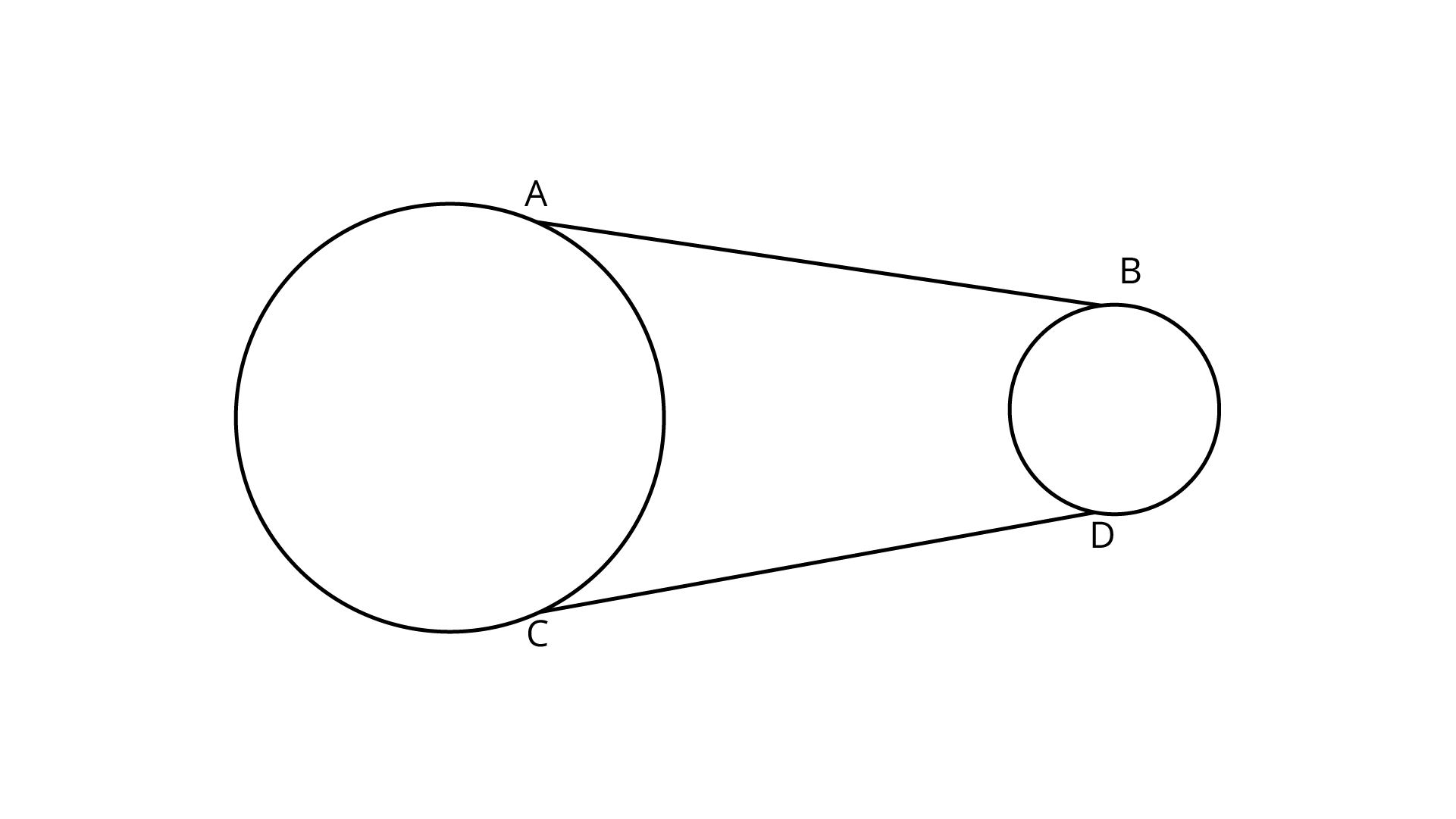
AS and CD are common tangent to two circles of unequal radius

$PA = PC$

(The length of tangents drawn from an internal point to a circle are equal)

Also, $PB = PD$

(The lengths of tangents drawn from an internal point to a circle are equal)

$\therefore PA - PB = PC - PD$

$\Rightarrow AB = CD$

Hence proved.

6. In figure, AB and CD are common tangents to two circles of equal radii. Prove that $AB  =  CD$ 

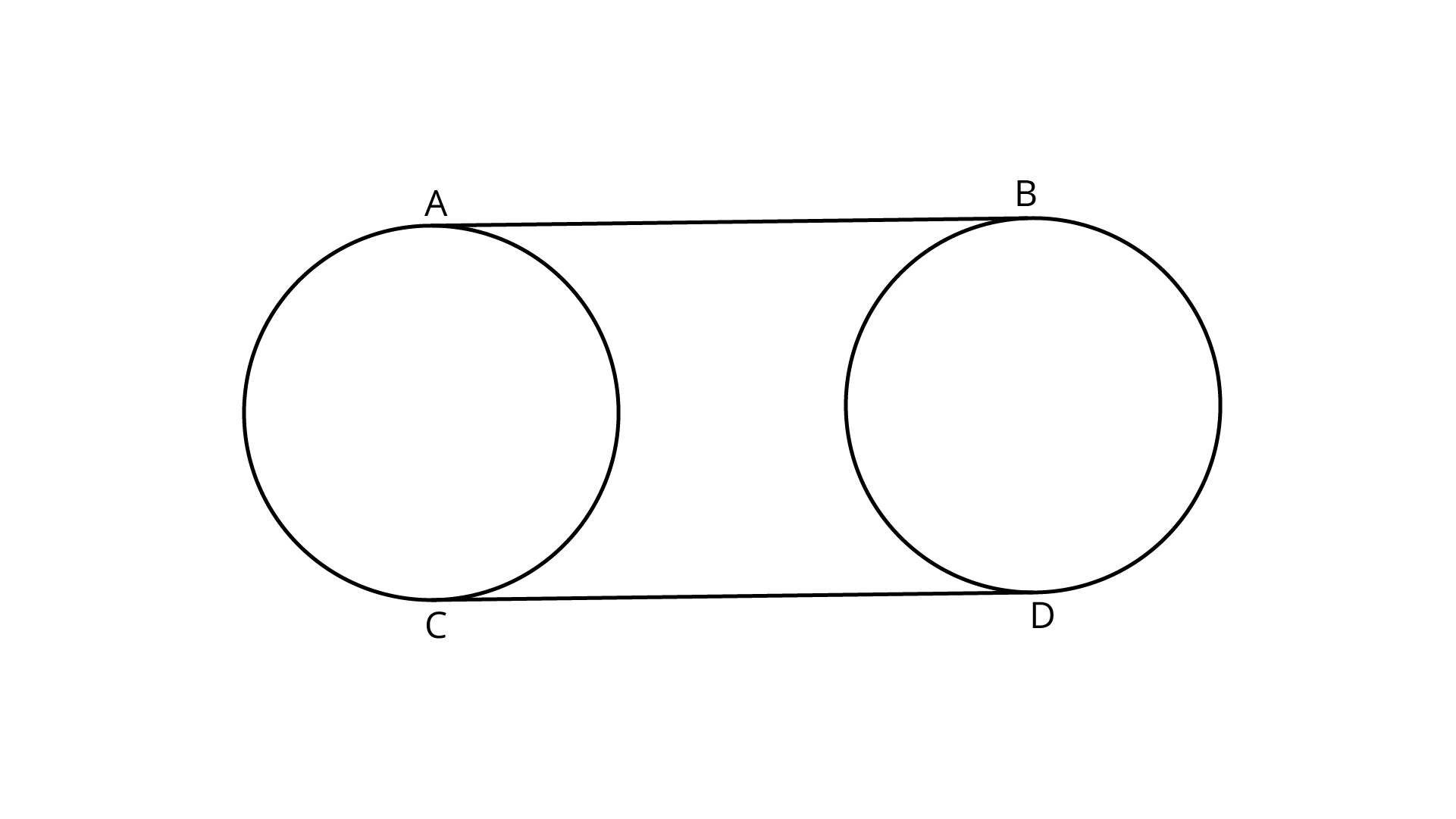
Ans:

AB and CD are tangents to two circles of equal radii.

Now, $\angle OAB = {90^\circ }$

(Tangent at any point of a circle is perpendicular to radius through the point of contact)

Thus, AC is a straight line. 

Also, $\angle OAB + \angle OCD = {180^\circ }$

$\therefore {\text{AB}}{\text{ = }}{\text{CD}}$

Similarly, BD is a straight line 

And $\angle {O^\prime }BA = \angle {O^\prime }DC = {90^\circ }$

Also, $AC = BD$ (radii of two circles are equal)

In quadrilateral ABCD, 

$\angle A = \angle B = \angle C = \angle D = {90^\circ }$

And $AC = BD$

ABCD is a rectangle 

Hence, $AB = CD$    (opposite sides of rectangle are equal)

7.In figure, common tangents AB and CD to two circles intersect at E. Prove that $AB  =  CD$

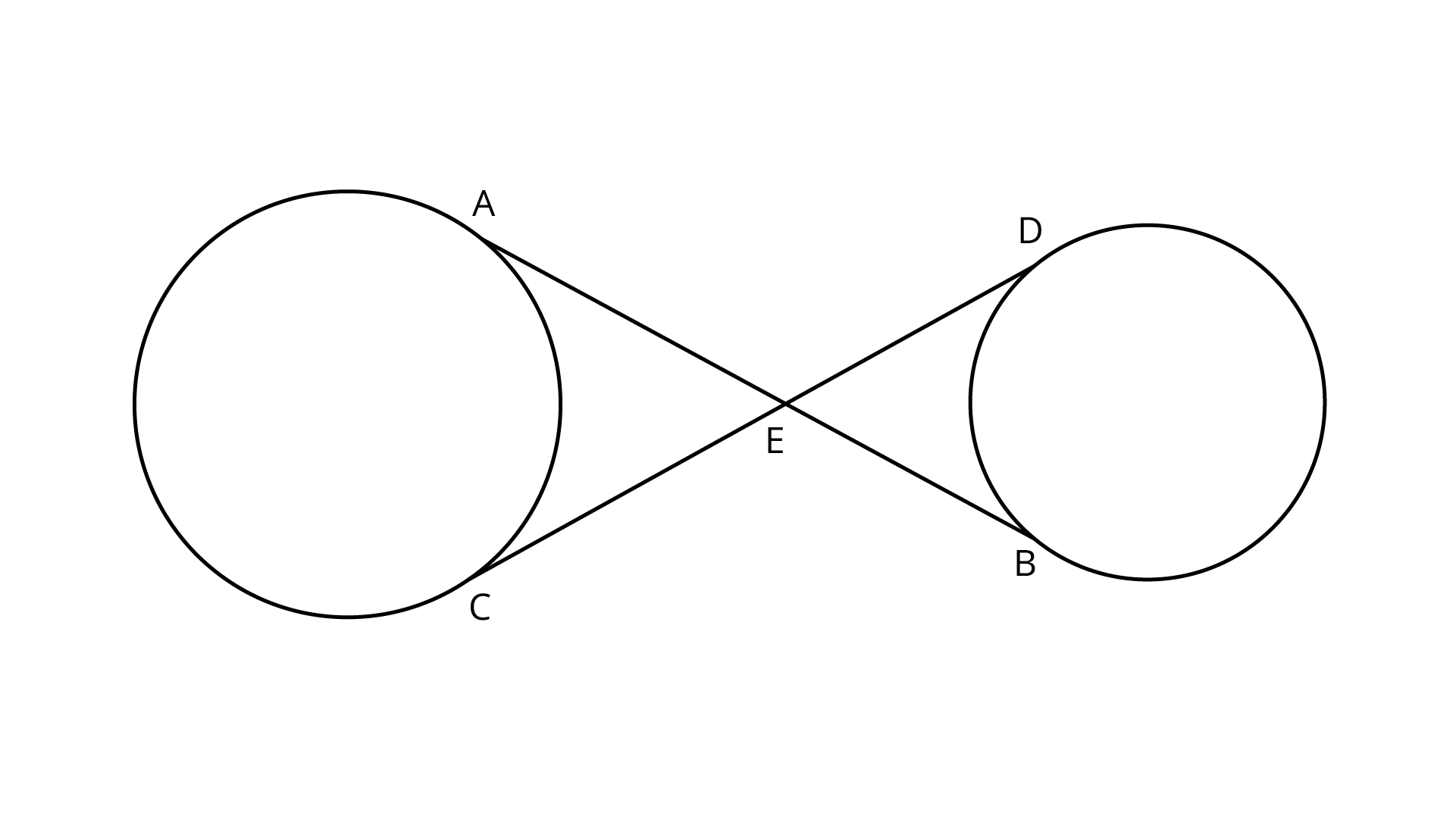
Ans:

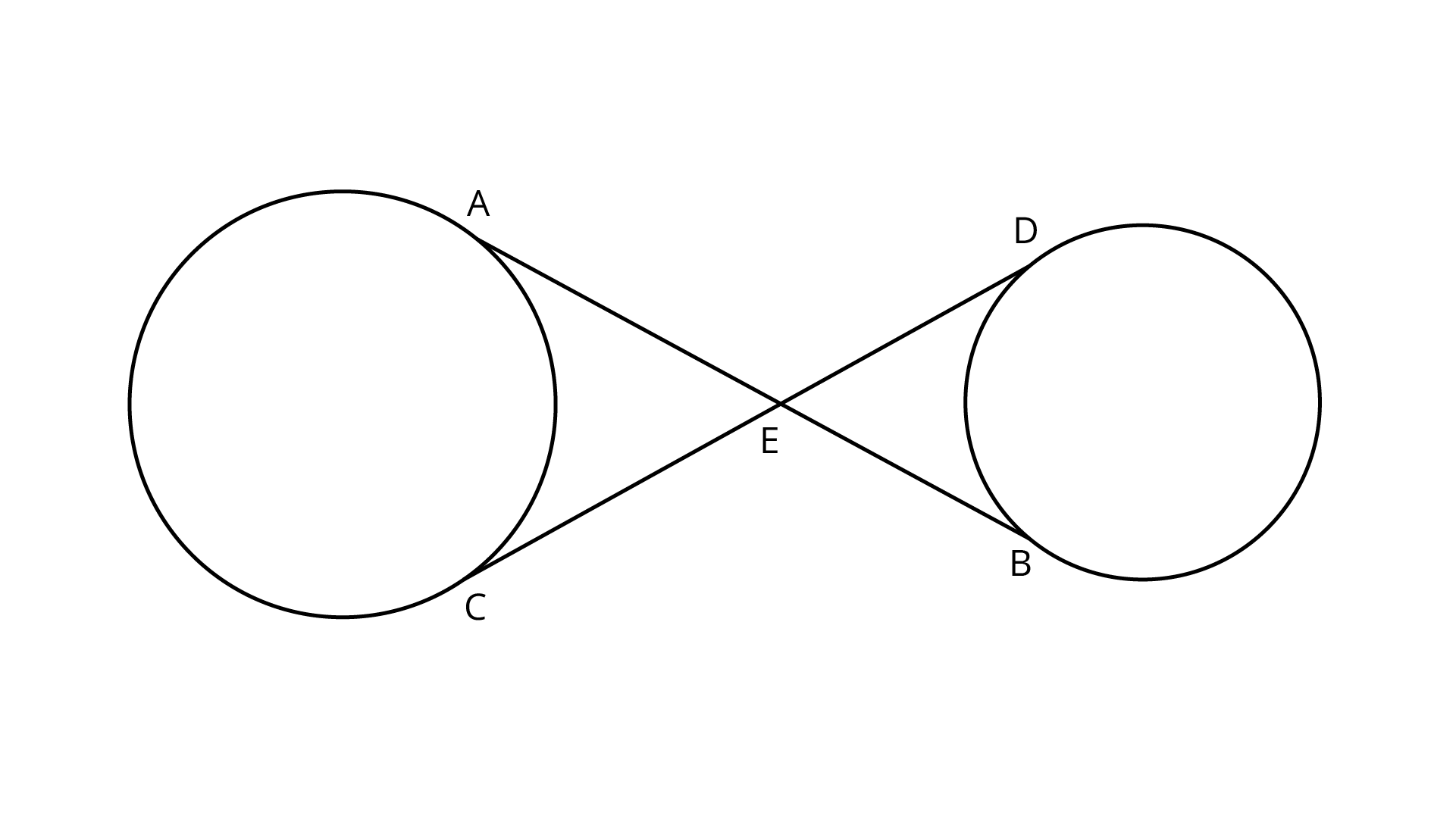
Common tangents AB and CD to two circles intersecting at E.

Proof: $EA = EC$... (i) 

(The lengths of tangents drawn from an internal point to a circle are equal) 

$EB = ED$.... (ii)

On adding Eqs. (i) And (ii), we get 

$EA + EB = EC + ED$

$\Rightarrow AB = CD$

Hence proved.

8. A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.

Ans:

Chord PQ is parallel to tangent at R.

(Angle between tangent and chord is equal to angle made by chord in alternate segment)

$\therefore \angle 2 = \angle 3$

$\Rightarrow PR = QR$ (Sides opposite to equal angles are equal)

$\Rightarrow PR = QR$

So, $R$ bisects PQ

9. Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.

Ans:

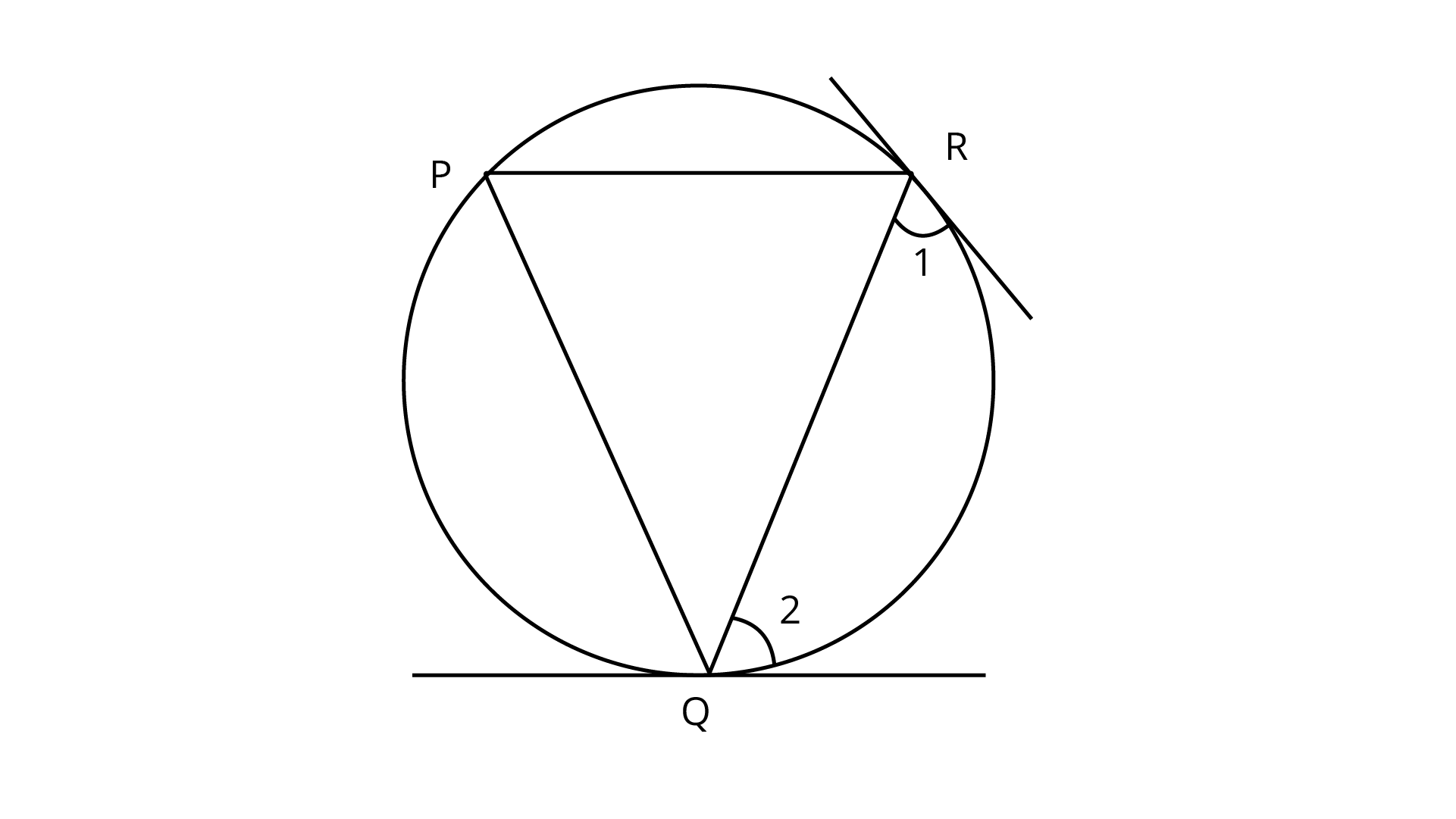
Tangents are drawn at the points R and Q.

Let P be another point on the circle, then, join PQ and PR.

Since, at point Q, there is a tangent.

$\therefore \angle 2 = \angle P$ (Angles in alternate segments are equal)

Since, at point $R$, there is a tangent.

$\therefore \angle 1 = \angle P$ (Angles in alternate segments are equal)

$\therefore \angle 1 = \angle 2 = \angle P$

Hence proved.

Question 10:

Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.

Ans:

Given, AB is the diameter of the circle.

A tangent is drawn from point A. Draw a chord CD parallel to the tangent MAN.

So, CD is a chord of the circle and OA is a radius of the circle.

$\angle MAO = {90^\circ }$

(Tangent at any point of a circle is perpendicular to the radius through the point of contact)

$\angle CEO = \angle MAO$   (Corresponding angles)

$\therefore \angle CEO = {90^\circ }$

Thus, OE bisects CD, 

(Perpendicular from centre of circle to chord bisects the chord)

Similarly, the diameter AB bisects all. 

Chords which are parallel to the tangent at the point A.

SAMPLE QUESTIONS

1. In Fig. 9.14 from an external point $P$ is a tangent $PT$, and a line segment $PAB$ is drawn to a circle with centre $O$. $ON$ is perpendicular on the chord $AB$. Prove that:

$\left( i \right)PA.PB = P{N^2} - A{N^2}$

$\left( {ii} \right)P{N^2} - A{N^2} = O{P^2} - O{T^2}$

$\left( {iii} \right)PA.PB = P{T^2}$

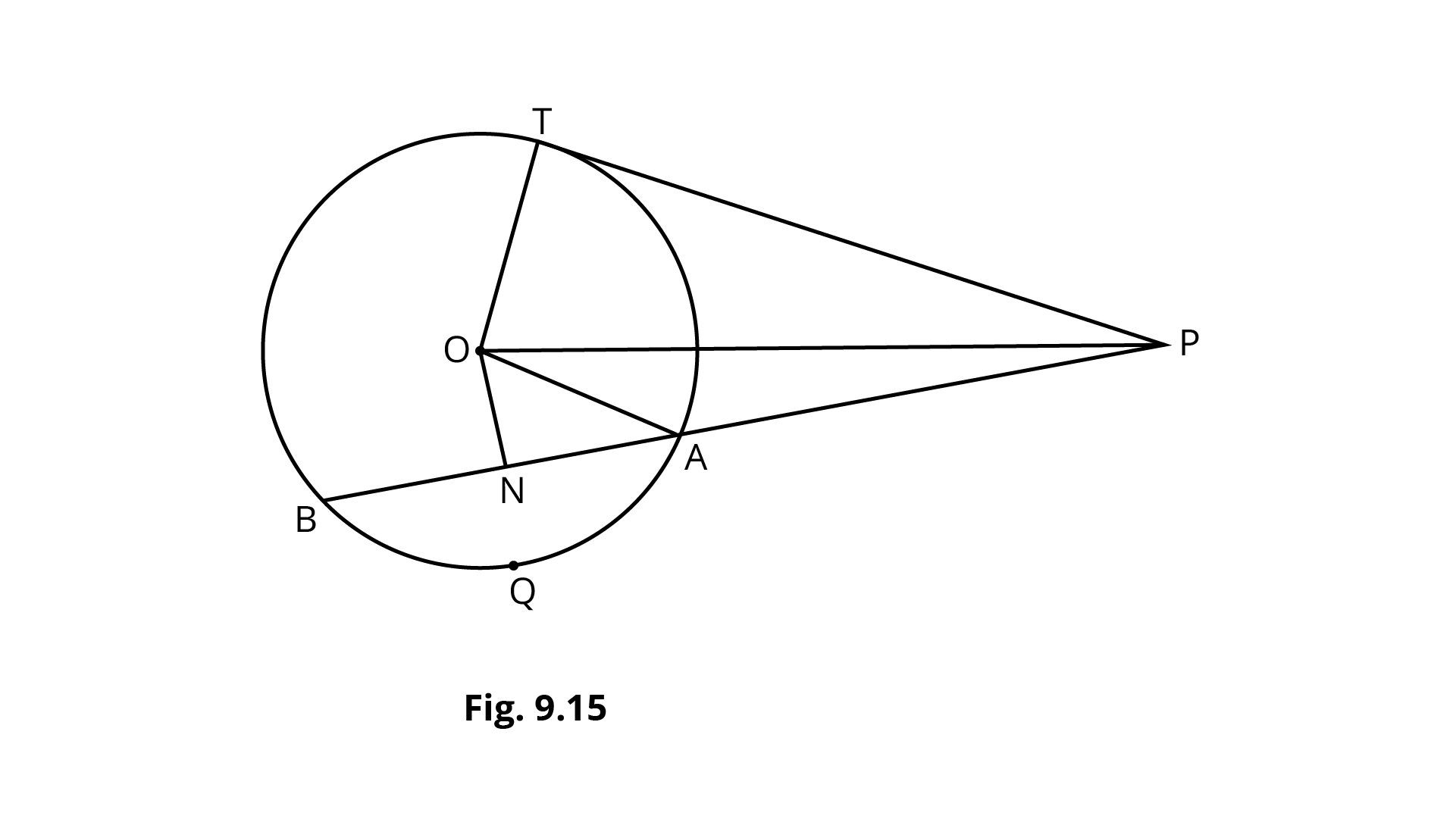
Ans:

$\left( i \right)$ From the figure it can be written,

$PA = \left( {PN - AN} \right)$ … (1)

$PB = \left( {PN + BN} \right)$ … (2)

Multiplying both the relations,

$\Rightarrow PA.PB = \left( {PN - AN} \right).\left( {PN + BN} \right)$

Since $ON$ in perpendicular to the chord $AB$, so using the theorem that ‘a line segment perpendicular to a chord bisects it’, the relation $AN = BN$ can be formed.

$\Rightarrow PA.PB = \left( {PN - AN} \right).\left( {PN + AN} \right)$

$\Rightarrow PA.PB = P{N^2} - A{N^2}$ 

$\left( {ii} \right)$ Now, in the right triangle $ONP$,

$P{N^2} = O{P^2} - O{N^2}$ … (3)

In the right triangle $ONA$,

$A{N^2} = O{A^2} - O{N^2}$ … (4)

Subtracting equation (4) from (3),

$\Rightarrow P{N^2} - A{N^2} = O{P^2} - O{N^2} - O{A^2} + O{N^2}$

$\Rightarrow P{N^2} - A{N^2} = O{P^2} - O{A^2}$ 

Clearly $OA = OT$ because they are the radius of the circle,

$\Rightarrow P{N^2} - A{N^2} = O{P^2} - O{T^2}$

$\left( {iii} \right)$ In the right triangle $OTP$ (tangent $PT$ is perpendicular of the radius $OT$),

$O{P^2} - O{T^2} = P{T^2}$

Using the result of $\left( {ii} \right)$,

$\Rightarrow P{N^2} - A{N^2} = P{T^2}$

Using the result of $\left( i \right)$,

$\Rightarrow PA.PB = P{T^2}$

2. If a circle touches the side $BC$ of a triangle $ABC$ at $P$ and extended sides $AB$ and $AC$ at $Q$ and $R$ respectively, prove that $AQ = \dfrac{1}{2}\left( {BC + CA + AB} \right)$.

Use the theorem that ‘tangents drawn from an external point are equal in length’.

Ans: The diagram of the given condition can be shown below: -

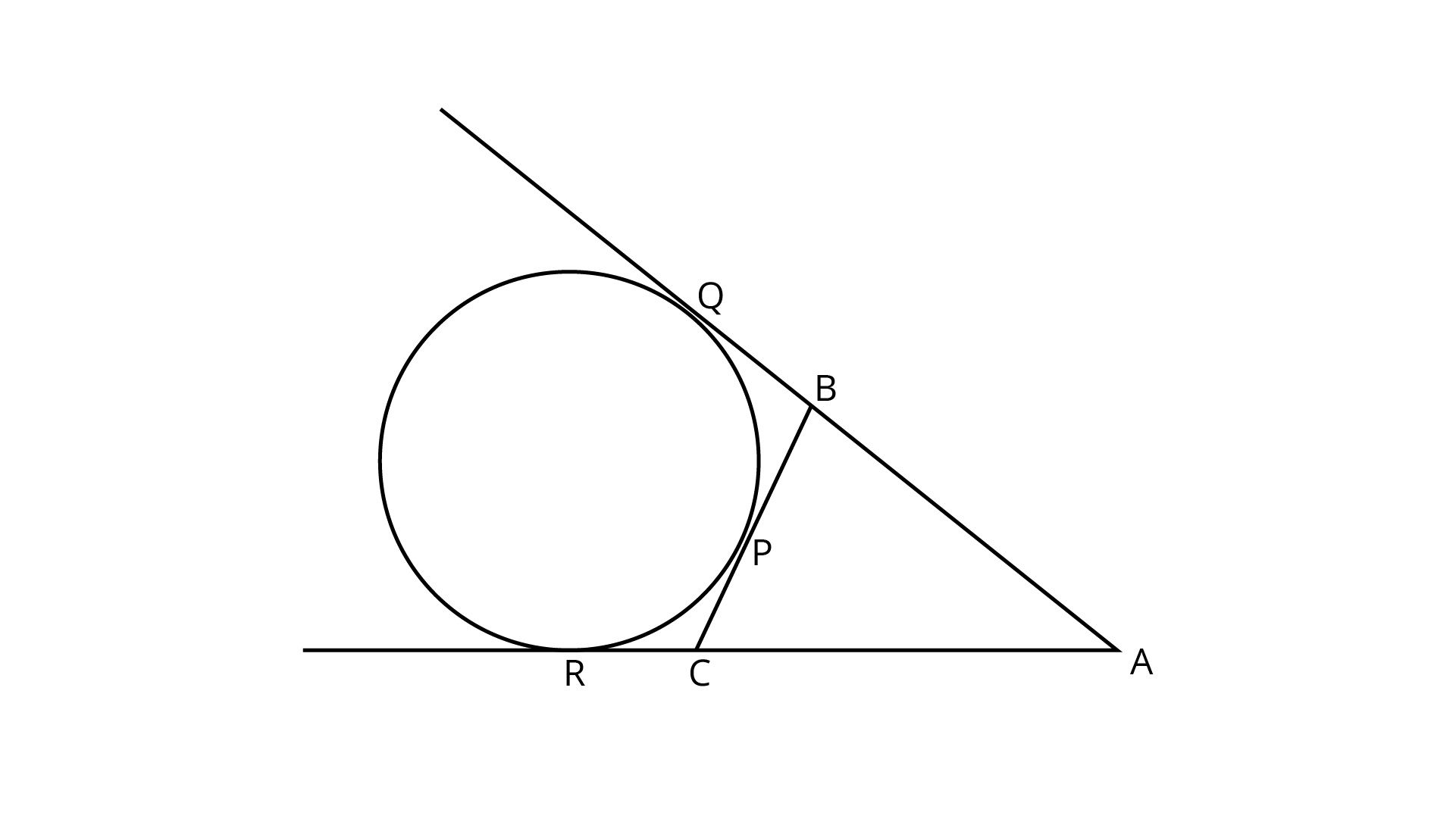
The tangents drawn from an external point on a circle are equal in length.

Considering point $A$ as the external point , $AR$ and $AQ$ as the tangents,

$\Rightarrow AQ = AR$

$\Rightarrow AQ = CA + CR$ 

Now, $CR = CP$ because $C$ is the external point , $CR$ and $CP$ are the tangents.

$\Rightarrow AQ = CA + CP$

$\Rightarrow AQ = CA + BC - PB$ 

Now, $PB = BQ$ because $B$ is the external point , $PB$ and $BQ$ are the tangents.

$\Rightarrow AQ = CA + BC - BQ$

$\Rightarrow AQ = CA + BC - \left( {AQ - AB} \right)$

$\Rightarrow 2AQ = CA + BC + AB$

$\Rightarrow AQ = \dfrac{1}{2}\left( {CA + BC + AB} \right)$ 

EXERCISE 9.4

1. A hexagon $ABCDEF$ circumscribe a circle, proving that $AB + CD + EF = BC + DE + FA$.

Ans: Assuming that the sides of the hexagon touches the circle at points  $G$, $H$, $I$, $J$, $K$ and $L$. The diagram of the given condition can be shown below: -

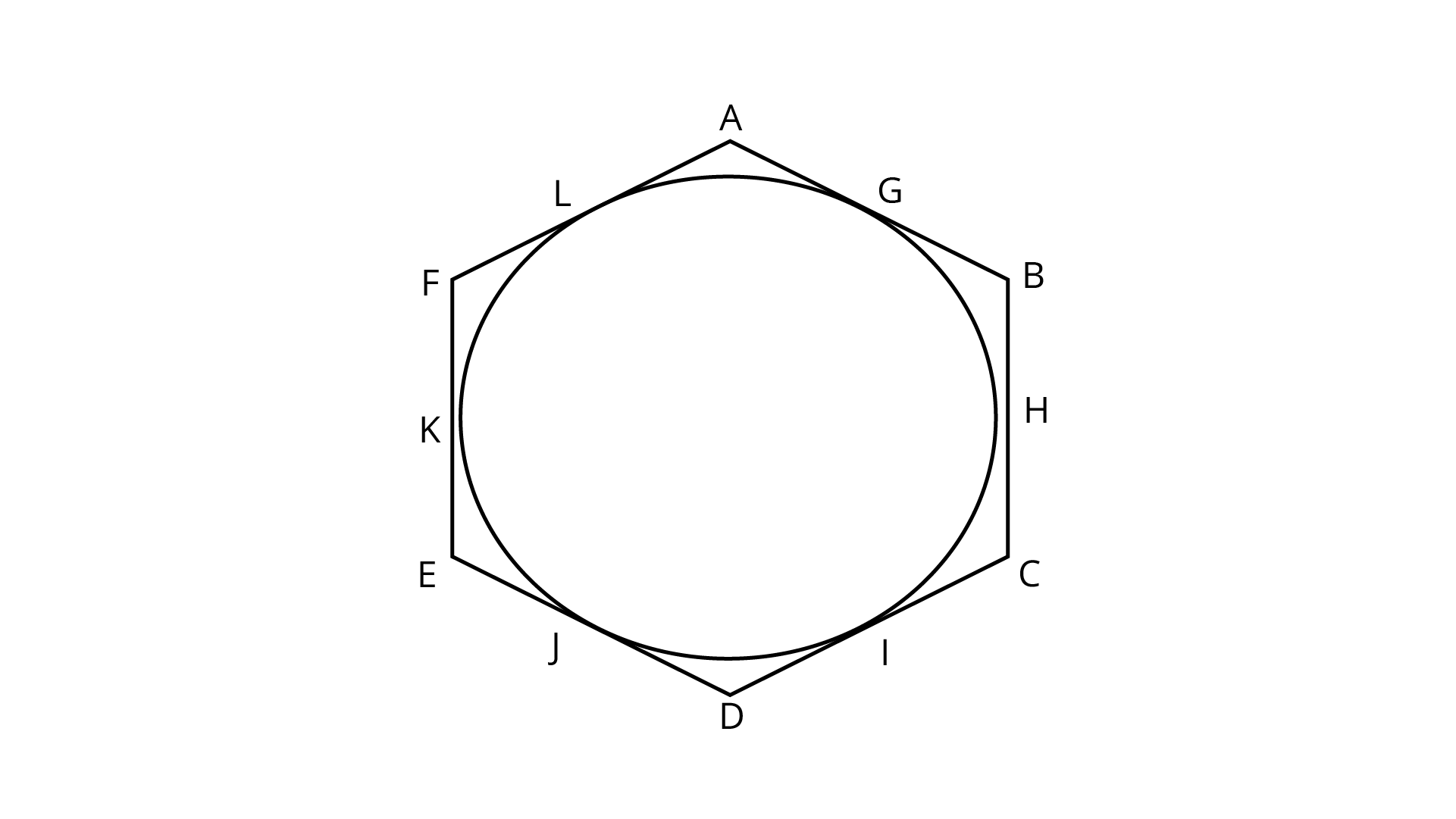
The tangents drawn from an external point on a circle are equal in length.

Considering point $A$ as the external point , $AG$ and $AL$ as the tangents,

$\Rightarrow AG = AL$ … (1)

Considering $B$ as the external point , $BG$ and $GH$ as the tangents,

$\Rightarrow BG = BH$ … (2)

Considering $C$ as the external point , $CI$ and $CH$ as the tangents,

$\Rightarrow CI = CH$ … (3)

Considering $D$ as the external point , $DI$ and $DJ$ as the tangents,

$\Rightarrow DI = DJ$ … (4)

Considering $E$ as the external point , $EK$ and $EJ$ as the tangents,

$\Rightarrow EK = EJ$ … (5)

Considering $F$ as the external point , $FK$ and $FL$ as the tangents,

$\Rightarrow FK = FL$ … (6)

Adding equations (1), (2), (3), (4), (5) and (6),

$\Rightarrow \left( {AG + BG} \right) + \left( {CI + DI} \right) + \left( {EK + FK} \right) = \left( {AL + FL} \right) + \left( {BH + CH} \right) + \left( {DJ + EJ} \right)$

$\Rightarrow AB + CD + EF = AF + BC + DE$

$\Rightarrow AB + CD + EF = BC + DE + FA$ 

2. Let $s$ denote the semi – perimeter of a triangle $ABC$ in which $BC = a$, $CA = b$ and $AB = c$. If a circle touches the sides $BC$, $CA$, $AB$ at $D$, $E$, $F$ respectively. Prove that $BD = s - b$.

Ans: The diagram of the given condition can be shown below: -

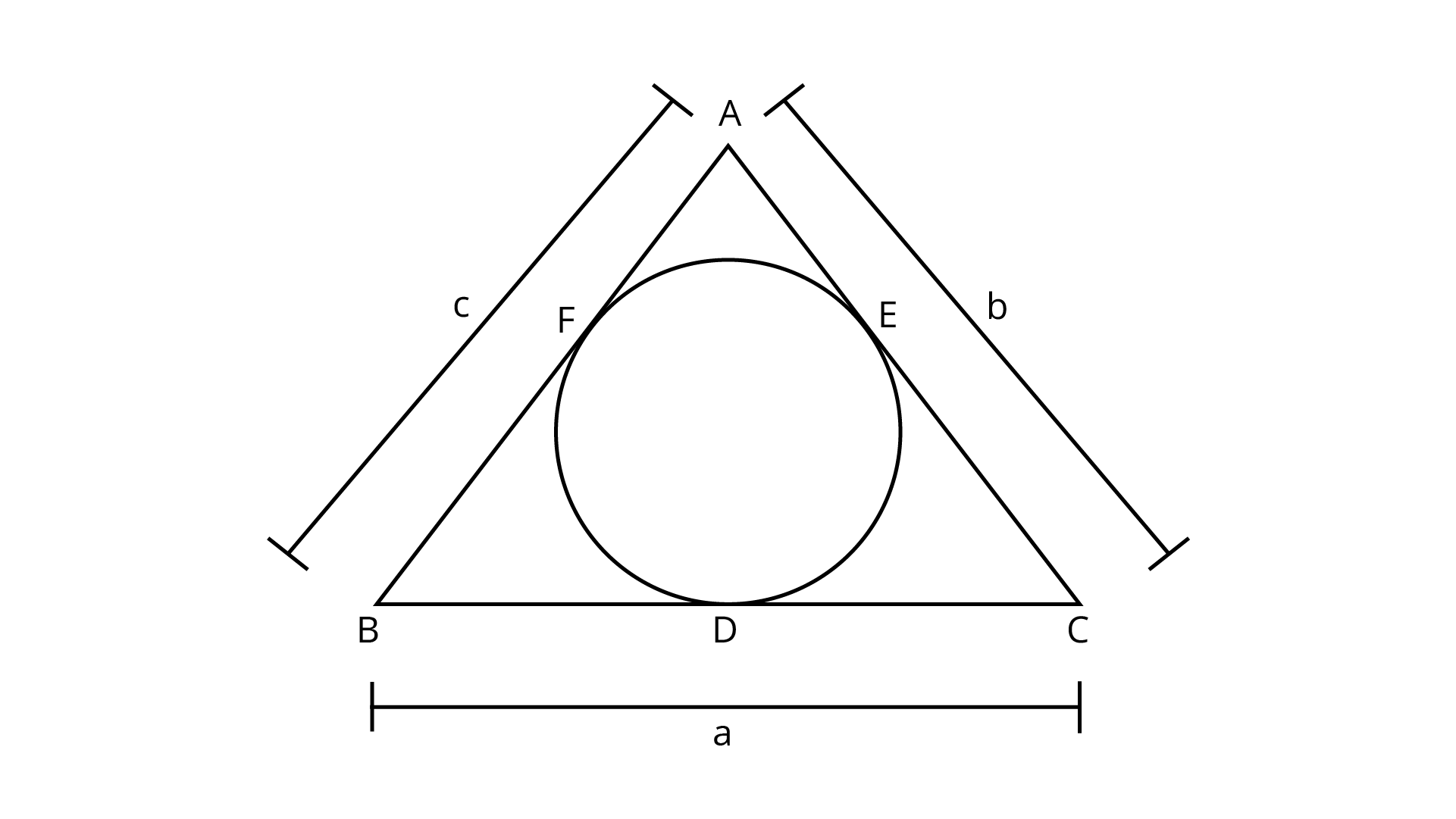
The tangents drawn from an external point on a circle are equal in length.

Considering point $B$ as the external point , $BD$ and $BF$ as the tangents,

$\Rightarrow BD = BF$

$\Rightarrow BD = c - AF$ 

Now, $AF = AE$ because $A$ is the external point , $AF$ and $AE$ are the tangents.

$\Rightarrow BD = c - AE$

$\Rightarrow BD = c - \left( {b - CE} \right)$

$\Rightarrow BD = c - b + CE$ 

Now, $CE = CD$ because $C$ is the external point , $CE$ and $CD$ are the tangents.

$\Rightarrow BD = c - b + CD$

$\Rightarrow BD = c - b + a - BD$

$\Rightarrow 2BD = a + c - b$

$\Rightarrow BD = \dfrac{{a + c - b}}{2}$ 

The semi – perimeter of a triangle is $s = \dfrac{{a + b + c}}{2}$, so substituting the value of $\left( {a + c} \right)$ from here,

$\Rightarrow BD = \dfrac{{2s - b - b}}{2}$

$\Rightarrow BD = \dfrac{{2\left( {s - b} \right)}}{2}$

$\Rightarrow BD = s - b$ 

3. From and external point $P$, two tangents, $PA$ and $PB$ are drawn to a circle with centre $O$. At one point $E$ on the circle tangent is drawn which intersects $PA$ and $PB$ at $C$ and $D$, respectively. If $PA = 10 cm$, find the perimeter of the triangle $PCD$.

Ans: The diagram of the given condition can be shown below: -

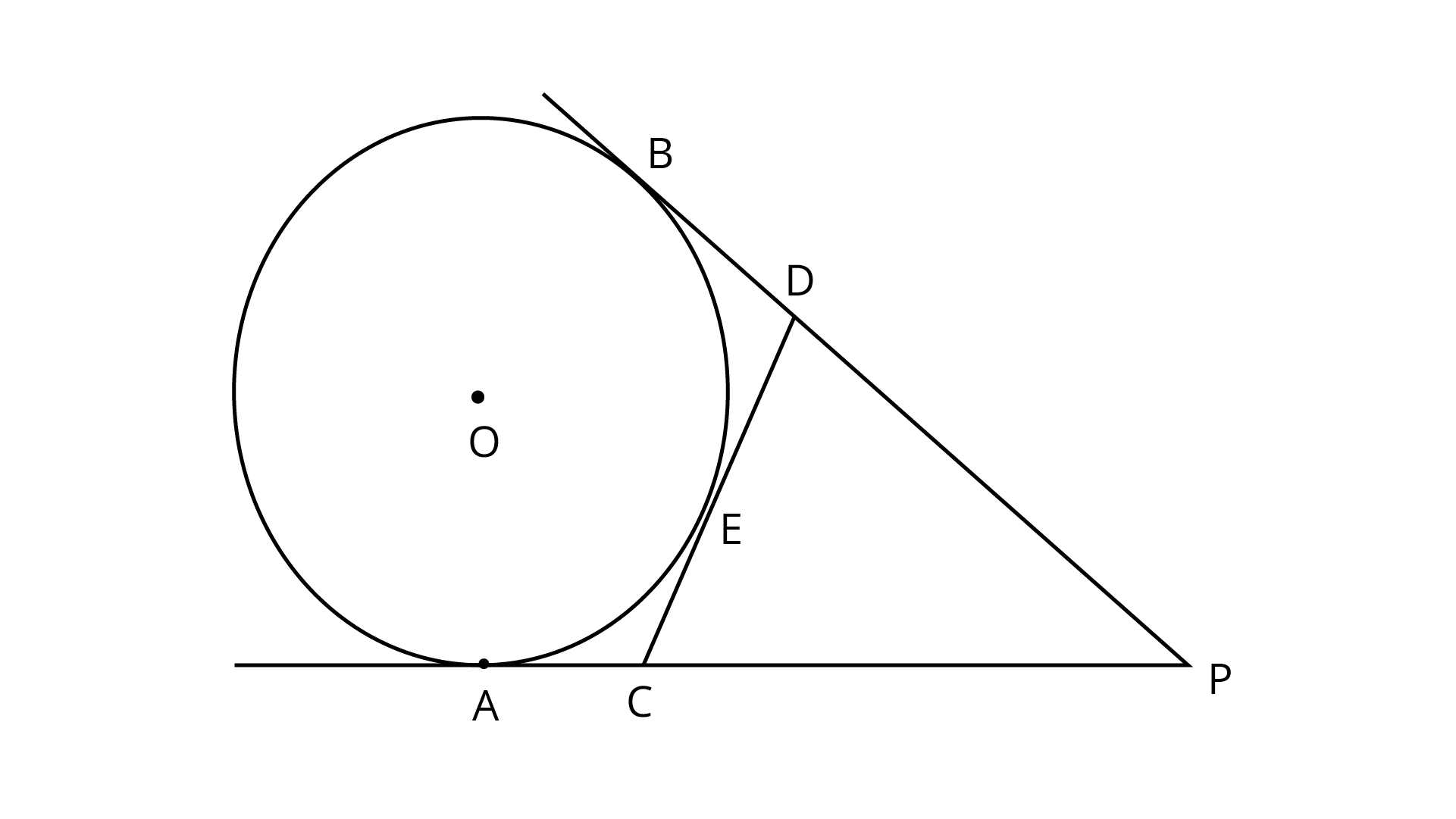
The perimeter of the triangle $PCD$ (let $S$) is

$\Rightarrow S = PC + CD + PD$

$\Rightarrow S = \left( {PA - CA} \right) + CD + \left( {PB - DB} \right)$

$\Rightarrow S = PA + PB + CD - \left( {CA + DB} \right)$ 

The tangents drawn from an external point on a circle are equal in length.

Considering point $C$ as the external point , $CA$ and $CE$ as the tangents,

$\Rightarrow CA = CE$ … (1)

Now, considering point $D$ as the external point , $DB$ and $DE$ as the tangents,

$\Rightarrow DB = DE$ … (2)

Adding equations (1) and (2),

$\Rightarrow \left( {CA + DB} \right) = CE + DE$

$\Rightarrow \left( {CA + DB} \right) = CD$ 

Substituting this relation in the perimeter,

$\Rightarrow S = PA + PB + CD - CD$

$\Rightarrow S = PA + PB$ 

Since $P$ is the external point, $PA$ and $PB$ are the tangents, so $PA = PB = 10{\text{ cm}}$.

$\Rightarrow S = \left( {10 + 10} \right){\text{ cm}}$

$\Rightarrow S = 20{\text{ cm}}$ 

4. If $AB$ is a chord of a circle with centre $O$, $AOC$ is a diameter and $AT$ is the tangent at $A$ as shown in Fig. 9.17. Prove that $\angle BAT = \angle ACB$.

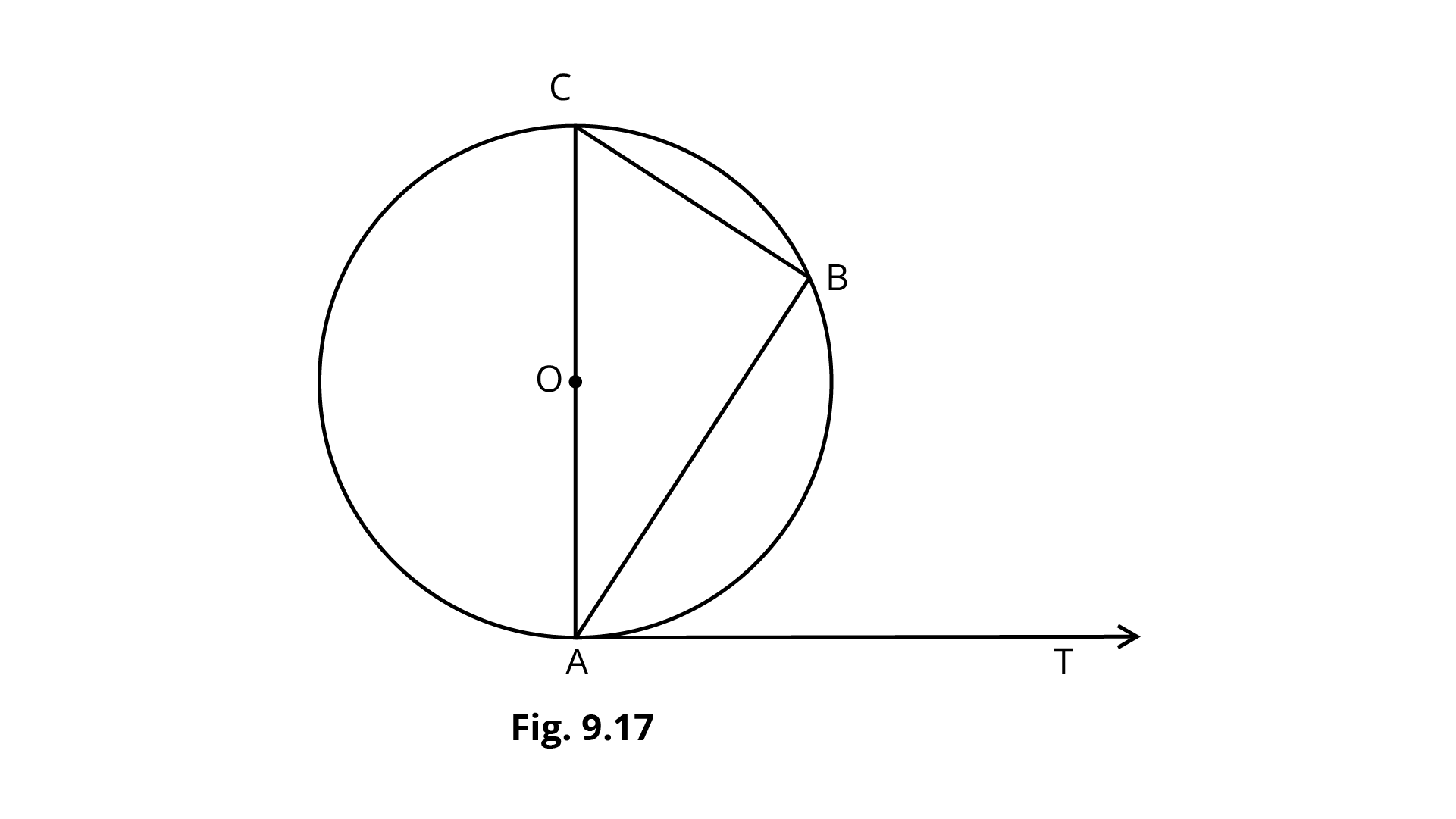
Ans: A tangent is perpendicular to the radius at the point of contact. Here $OA$ is the radius and $AT$ is the tangent, so $OA$ is perpendicular to $AT$.

$\angle BAT = \angle OAT - \angle OAB$

$\angle BAT = {90^ \circ } - \angle OAB$ 

$\angle BAT = {90^ \circ } - \angle CAB$ … (1)

Now, the angle in a semi – circle is a right angle. Since $AOC$ is the diameter so the arc $ABC$ along with the diameter is a semi – circle.

$\Rightarrow \angle ABC = {90^ \circ }$

$\Rightarrow \angle ACB = {90^ \circ } - \angle CAB$ 

Substituting the value of $\angle CAB$ in equation (1),

$\Rightarrow \angle BAT = {90^ \circ } - \left( {{{90}^ \circ } - \angle ACB} \right)$

$\Rightarrow \angle BAT = \angle ACB$ 

5. Two circles with centres $O$ and $O'$ of radii $3 cm$ and $4 cm$, respectively intersect at two points $P$ and $Q$ such that $OP$ and $O'P$ are tangents to the two circles. Find the length of the common chord $PQ$.

Ans: The diagram of the given condition can be shown below: -

Here $O'P$ is the tangent to the circle with radius $3{\text{ cm}}$ and $OP$ is the tangent to the circle with radius $4{\text{ cm}}$. $OP$ and $O'P$ are the radius of the two circles.

Radius is perpendicular to the tangent at the point of contact so $OP$ perpendicular to $O'P$. Now, in the right triangle $OPO'$ using the Pythagoras theorem,

$\Rightarrow OO' = \sqrt {{{\left( {OP} \right)}^2} + {{\left( {O'P} \right)}^2}}$

$\Rightarrow OO' = \sqrt {{3^2} + {4^2}}$

$\Rightarrow OO' = 5{\text{ cm}}$ 

Here $OO'$ is the perpendicular bisector of the chord $PQ$ which can be proved by using the $S - S - S$ congruency criteria in the right triangles $OPO'$ and $OQO'$.

$\Rightarrow PM = QM = \dfrac{1}{2}PQ$ … (1)

$OP$ and $O'P$ can be considered as the height and base of the triangles, so its area is $\dfrac{1}{2} \times OP \times O'P$. 

Also $PM$ and $OO'$ can be considered as the base and height of the same triangle, so its area can also be $\dfrac{1}{2} \times OO' \times PM$.

$\Rightarrow \dfrac{1}{2} \times OP \times O'P = \dfrac{1}{2} \times OO' \times PM$

$\Rightarrow \dfrac{1}{2} \times 3 \times 4 = \dfrac{1}{2} \times 5 \times PM$

$\Rightarrow PM = \dfrac{{12}}{5}$

$\Rightarrow PM = 2.4{\text{ cm}}$ 

Using relation (1),

$\Rightarrow PQ = 2PM$

$\Rightarrow PQ = 2 \times 2.4$

$\Rightarrow PQ = 4.8{\text{ cm}}$ 

6. In a right triangle $ABC$ in which $\angle B = 9{0^o}$, a circle is drawn with $AB$ as diameter intersecting the hypotenuse $AC$ at $P$. Prove that the tangent to the circle at $P$ bisects $BC$.

Ans: The diagram of the given condition can be shown below: -

In the above figure, $PM$ is the tangent intersecting the side $BC$ at $M$.

The tangents drawn from an external point are equal in length. Considering $M$ as the external point, $BM$ and $PM$ as the tangents,

$\Rightarrow BM = PM$ … (1)

Assuming $\angle PBM = \theta$, it is found $\angle PBA = \left( {{{90}^ \circ } - \theta } \right)$ because $\angle B = {90^ \circ }$. Since angle in a semi – circle is a right angle that means $\angle APB = {90^ \circ }$. So in the right triangle $APB$, it is found $\angle PAB = \theta $.

Now, in right triangle $ABC$,

$\Rightarrow \angle A + \angle B + \angle C = {180^ \circ }$

$\Rightarrow \angle C = {180^ \circ } - \left( {{{90}^ \circ } + \theta } \right)$

$\Rightarrow \angle C = {90^ \circ } - \theta$ 

Since $\angle APB = {90^ \circ }$ that means $\angle CPB = {90^ \circ }$ because $AC$ is a straight line. Since $\angle PBM = \theta $ and it is already obtained $BM = PM$ which makes the triangle $PBM$ an isosceles triangle. Therefore, $\angle BPM = \theta $ which gives $\angle CPM = \left( {{{90}^ \circ } - \theta } \right)$.

Now, in the triangle $PMC$ it is obtained $\angle CPM = \angle PCM = \left( {{{90}^ \circ } - \theta } \right)$ that means this triangle is also an isosceles triangle where $PM = CM$. Hence, using relation (1),

$\Rightarrow BM = CM$

The above relation states that the tangent bisects $BC$.

7. In figure 9.18 tangents $PQ$ and $PR$ are drawn to a circle such that $\angle RPQ = 3{0^o}$. A chord $RS$ is drawn parallel to the tangent $PQ$. Find the $\angle RQS$.

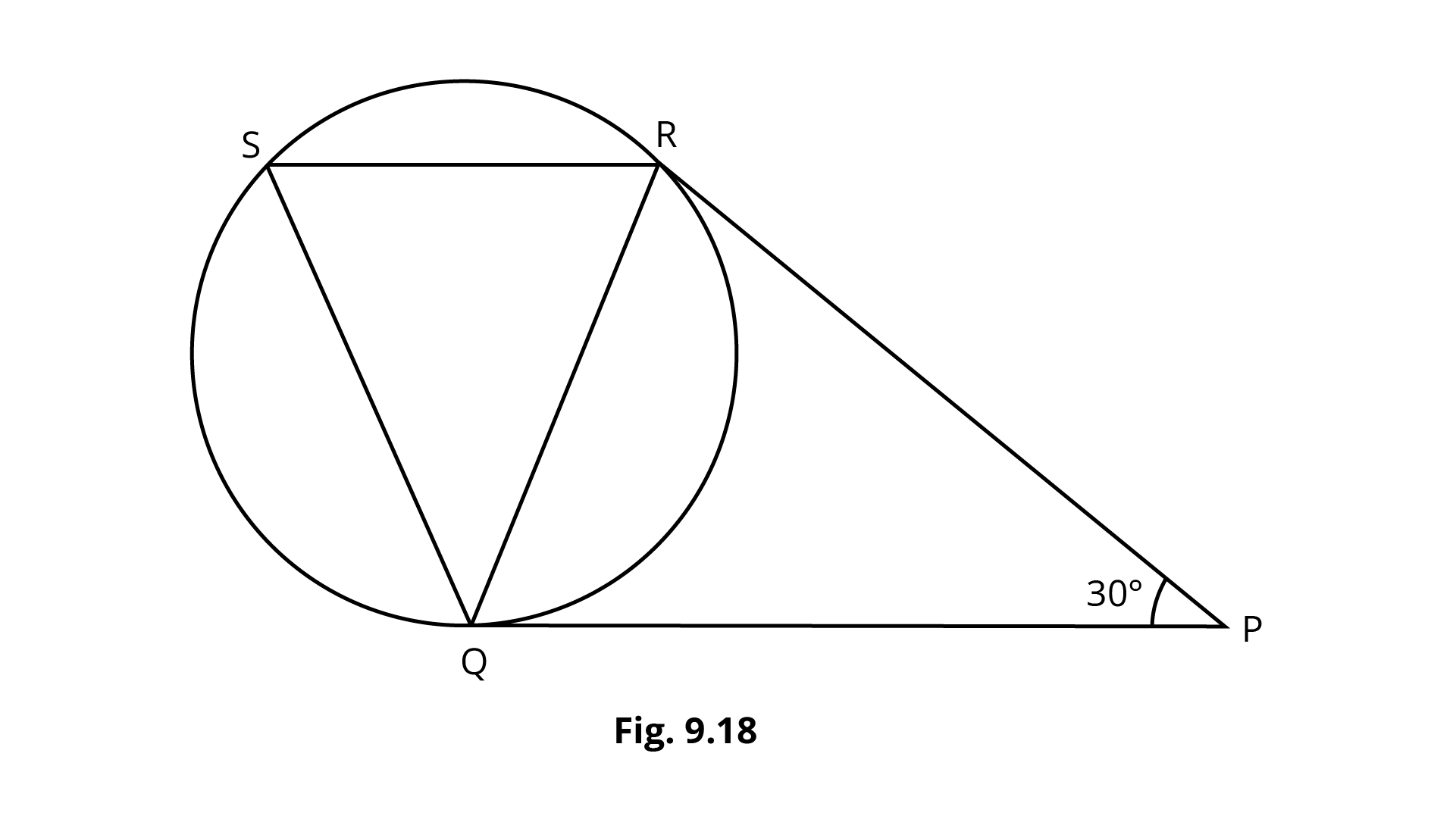
Ans:

In the above figure a line $QM$ perpendicular to the tangent $PQ$ is constructed. Since $RS$ is parallel to $PQ$ so $QM$ is also perpendicular to $RS$ (co – interior angles property).

Radius is perpendicular to the tangent at the point of contact that only means here the line $QM$ is passing through the centre of the circle.

Also the perpendicular from the centre of the circle bisects the chord that means $RM = SM$. Now, in the right triangles $QMR$ and $QMS$,

$RM = SM$

$\angle QMR = \angle SMR = {90^ \circ }$

$QM = QM$ (common side)

Therefore, $\Delta QMR \cong \Delta QMS$ by $S - S - S$ congruency criteria. So $QR = SR$ and the triangle $SRQ$ is an isosceles triangle.

$\angle QRS = \angle QSR$ … (1)

Now, the tangents drawn from an external point are equal in length so $PQ = PR$ and $\angle PQR = \angle PRQ$. Since $\angle RPQ = {30^ \circ }$ so $\angle PQR = \angle PRQ = {75^ \circ }$.

Now, $\angle PQR = \angle QRS = {75^ \circ }$, because they are alternate angles. Using relation (1), $\angle QRS = \angle QSR = {75^ \circ }$.

In the triangle $QSR$,

$\Rightarrow \angle QRS + \angle QSR + \angle RQS = {180^ \circ }$

$\Rightarrow \angle RQS = {180^ \circ } - \left( {{{75}^ \circ } + {{75}^ \circ }} \right)$

$\Rightarrow \angle RQS = {30^ \circ }$ 

8. $AB$ is a diameter and $AC$ is a chord of a circle with centre $O$ such that $\angle BAC = 3{0^o}$. The tangent at $C$ intersects extended $AB$ at a point $D$. Prove that $BC = BD$.

Ans: The diagram of the given condition can be shown below: -

Since $AB$ is a diameter so the arc $ACB$ along with the diameter forms a semi – circle. The angle in a semi circle is a right angle.

$\Rightarrow \angle ACB = {90^ \circ }$

In triangle $ABC$,

$\Rightarrow \angle ACB + \angle ABC + \angle BAC = {180^ \circ }$

$\Rightarrow \angle ABC = {180^ \circ } - \left( {{{90}^ \circ } + {{30}^ \circ }} \right)$

$\Rightarrow \angle ABC = {60^ \circ }$ 

Therefore, $\angle DBC = \left( {{{180}^ \circ } - {{60}^ \circ }} \right) = {120^ \circ }$ because $ABD$ is a straight line.

$OC$ is joined. Since $OC$ is the radius and $DC$ is the tangent and the radius is perpendicular to the tangent at the point of contact, so $QC$ is perpendicular to $DC$.

In the triangle $OBC$, $OC = OB$ as both are radius, so $\angle OCB = \angle OBC = {60^ \circ }$. This results in $\angle DCB = \left( {{{90}^ \circ } - {{60}^ \circ }} \right) = {30^ \circ }$. Now, in triangle $DBC$,

$\Rightarrow \angle DCB + \angle DBC + \angle CDB = {180^ \circ }$

$\Rightarrow \angle CDB = {180^ \circ } - \left( {{{120}^ \circ } + {{30}^ \circ }} \right)$

$\Rightarrow \angle CDB = {30^ \circ }$ 

So it is obtained $\angle DCB = \angle CDB = {30^ \circ }$ that means triangle $DBC$ is an isosceles triangle where $BC = BD$.

9. Prove that the tangent drawn at the mid – point of an arc of a circle is parallel to the chord joining the end points of the arc.

Ans: The diagram of the given condition can be shown below: -

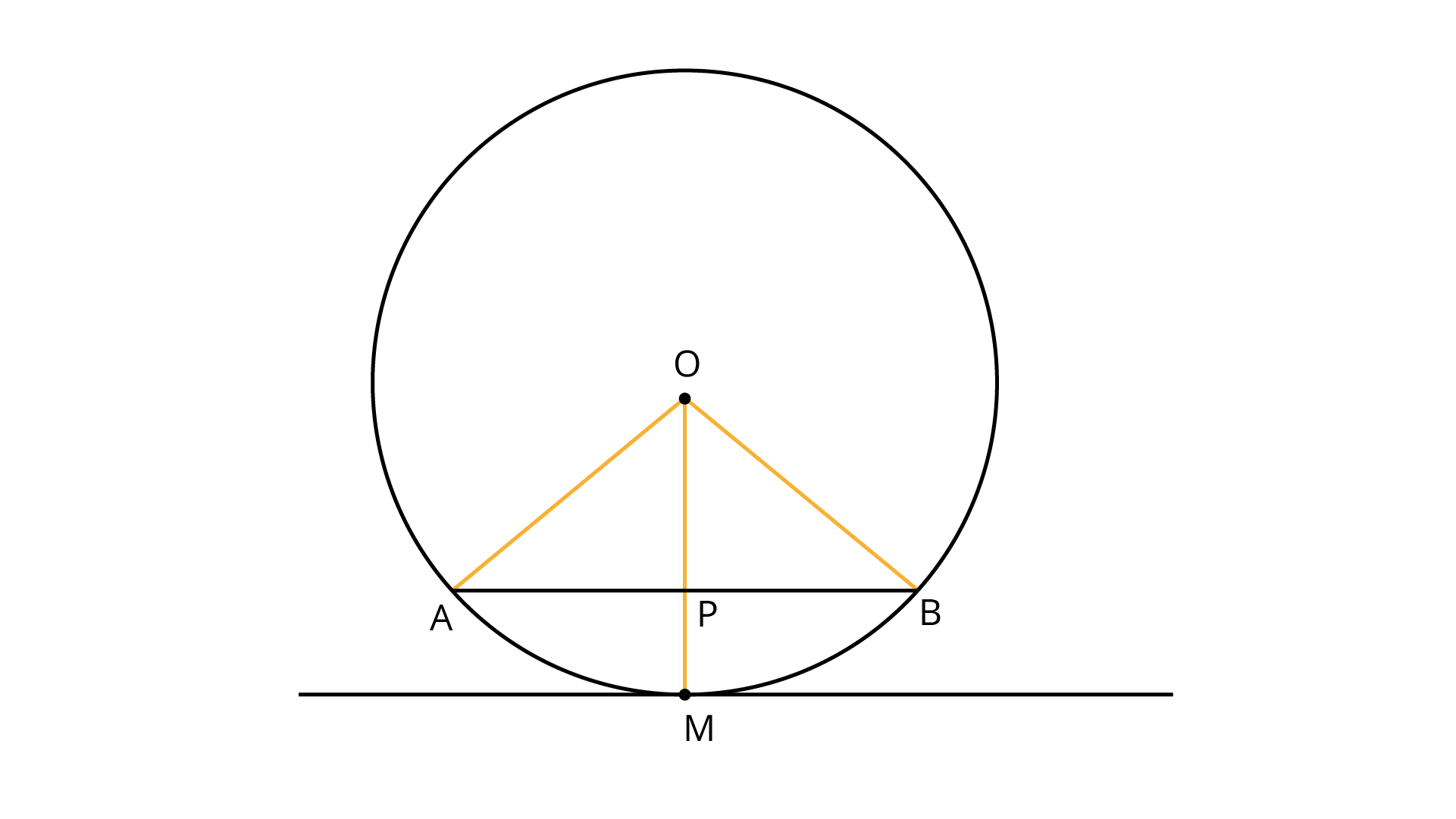
Points $A$ and $B$ are taken on the circle with centre $O$. $OA$ and $OB$ are joined. The point $M$ is the mid – point of the arc $AB$. $OM$ is also joined.

Equal arcs subtend equal angles at the center of the circle, so $\angle AOM = \angle BOM$. Now, $AB$ is joined that intersects $OM$ at $P$. Therefore, in triangles $AOP$ and $BOP$,

$OA = OB$ (since both are radius)

$\angle AOP = \angle BOP$

$OP = OP$ (common sides)

Therefore, triangles $AOP \cong BOP$ by $S - A - S$ congruency criteria. Hence, $\angle OPA = \angle OPB = {90^ \circ }$ because $APB$ is a straight line. It means $OP$ or $OM$ is perpendicular to $AB$.

Now, the radius is perpendicular to the tangent at the point of contact which states that $OM$ is perpendicular to the tangent at $M$.

Since $OM$ is perpendicular to both the chord $AB$ and the tangent that only means they must be parallel to each other.

10. In Fig. 9.19, the common tangent $AB$ and $CD$ to two circles with centre $O$ and $O'$ intersect at $E$. Prove that the points $O$, $E$, $O'$ are collinear.

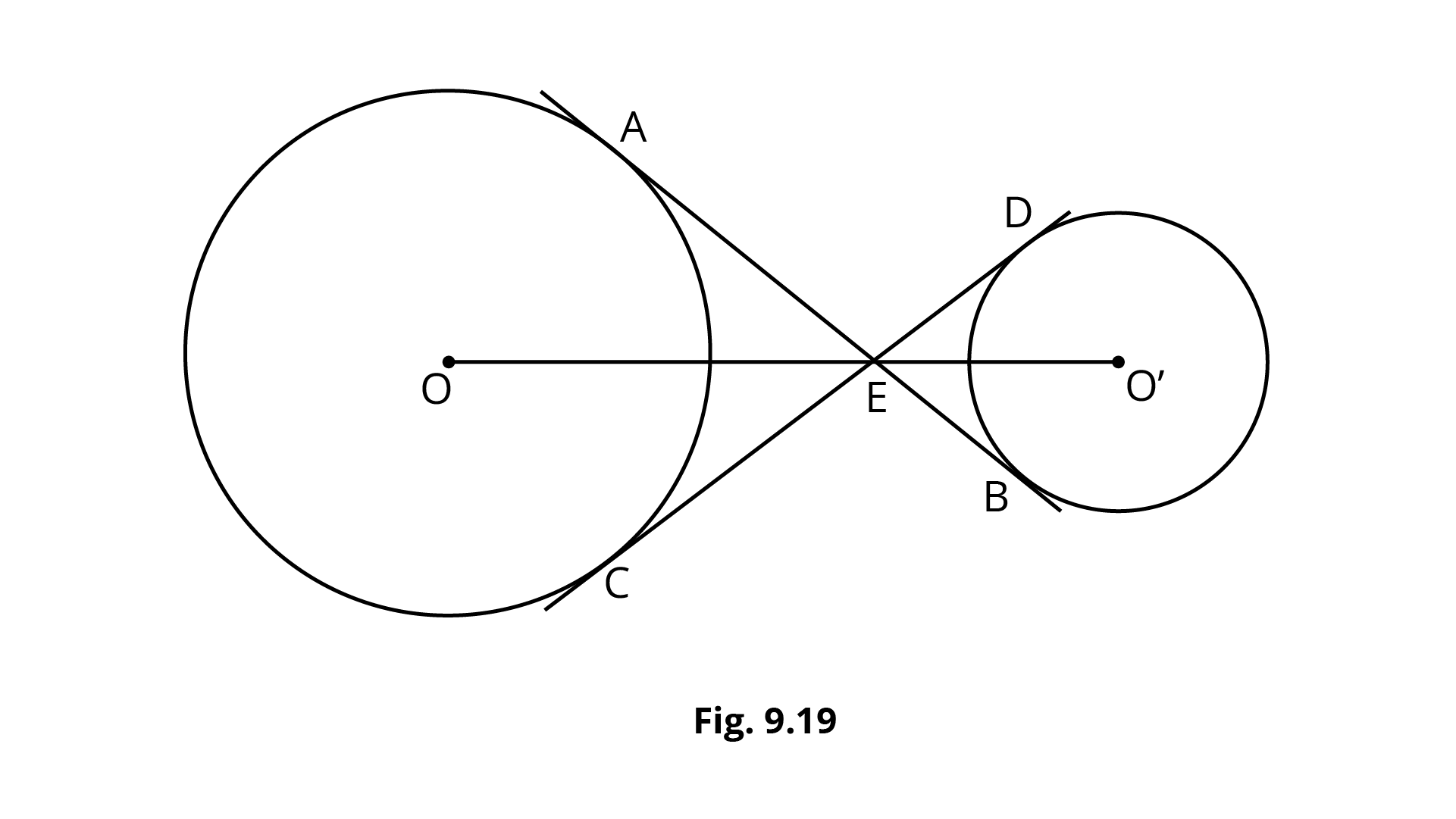
Ans:

In the above figure $OA$, $OC$ and $O'C$, $O'D$ are joined in the two circles respectively.

In triangles $OAE$ and $OCE$,

$\angle OAE = \angle OCE = {90^ \circ }$ (radius is perpendicular to the tangent)

$OE = OE$ (common side)

$OA = OC$ (radii of the circle)

Therefore, $\Delta OAE \cong \Delta OCE$ by $R - H - S$ congruency criteria.

$\angle AEO = \angle CEO$ … (1)

Now, in triangles $O'DE$ and $O'BE$,

$\angle O'DE = \angle O'BE = {90^ \circ }$ (radius is perpendicular to the tangent)

$O'E = O'E$ (common side)

$O'D = O'B$ (radii of the circle)

Therefore, $\Delta O'DE \cong \Delta O'BE$ by $R - H - S$ congruency criteria.

$\angle O'ED = \angle O'EB$ … (2)

Since, $\angle AED$ and $\angle CEB$ are vertically opposite angles.

$\angle AED = \angle CEB$ … (3)

The sum of all the angles around point $E$ is ${360^ \circ }$.

$\Rightarrow \left( {\angle AEO + \angle CEO} \right) + \left( {\angle O'ED + \angle O'EB} \right) + \left( {\angle AED + \angle CEB} \right) = {360^ \circ }$

Using relations (1), (2) and (3),

$\Rightarrow \left( {2\angle AEO} \right) + \left( {2\angle O'ED} \right) + \left( {2\angle AED} \right) = {360^ \circ }$

$\Rightarrow \angle AEO + \angle AED + \angle O'ED = {180^ \circ }$ 

The above relation states that $OEO'$ is a straight line, therefore the points $O$, $E$, $O'$ are collinear.

11. In Fig. 9.20, $O$ is the centre of the circle of radius $5 cm$. $T$ is a point such that $OT = 13 cm$ and $OT$ intersects the circle at $E$. If $AB$ is the tangent to the circle at $E$, find the length of $AB$.

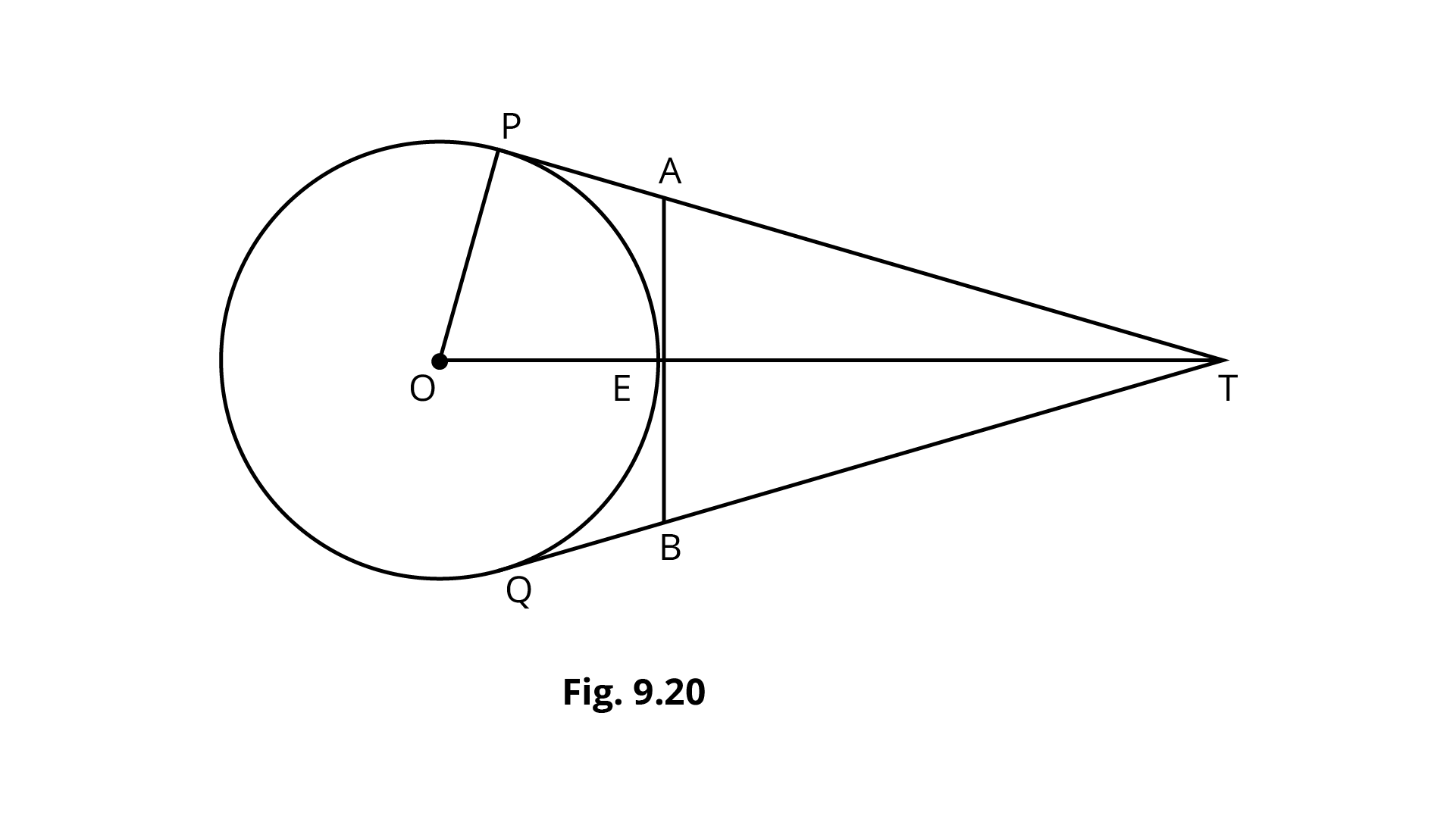
Ans:

The tangent is perpendicular to the radius at the point of contact.

$\Rightarrow \angle OPT = {90^ \circ }$

In right triangle $OPT$ using the Pythagoras theorem,

$\Rightarrow O{P^2} + P{T^2} = O{T^2}$

$\Rightarrow PT = \sqrt {{{\left( {13} \right)}^2} - {{\left( 5 \right)}^2}}$

$\Rightarrow PT = 12{\text{ cm}}$ 

Since $AB$ is a tangent at $E$ and $OE$ is radius, so $OE$ is perpendicular to $AB$. The length of $ET$ is,

$\Rightarrow ET = OT - OE$

$\Rightarrow ET = 13 - 5$

$\Rightarrow ET = 8{\text{ cm}}$ 

Assuming $\angle OTP = \theta $, in the right triangle $OPT$,

$\Rightarrow \tan \theta  = \dfrac{{OP}}{{PT}}$

$\Rightarrow \tan \theta  = \dfrac{5}{{12}}$ … (1)

Also, in right triangle $AET$,

$\Rightarrow \tan \theta  = \dfrac{{AE}}{{ET}}$

$\Rightarrow \tan \theta  = \dfrac{{AE}}{8}$ … (2)

From relations (1) and (2),

$\Rightarrow \dfrac{{AE}}{8} = \dfrac{5}{{12}}$

$\Rightarrow AE = \dfrac{{10}}{3}{\text{ cm}}$ 

Now, $QT = PT = 12{\text{ cm}}$, because they are the tangents from the same external point. So, following the same steps in right triangles $OQT$ and $BET$,

$\Rightarrow BE = \dfrac{{10}}{3}{\text{ cm}}$

Adding $AE$ and $BE$,

$\Rightarrow AB = AE + BE$

$\Rightarrow AB = \left( {\dfrac{{10}}{3} + \dfrac{{10}}{3}} \right){\text{ cm}}$

$\Rightarrow AB = \dfrac{{20}}{3}{\text{ cm}}$ 

12. In Fig. 9.21. The tangent at a point $C$ of a circle and a diameter $AB$ when extended intersect at $P$. If $\angle PCA = 11{0^o}$, find $\angle CBA$.

Ans:

In the above figure $OC$ is joined. The tangent is perpendicular to the radius at the point of contact. Here $OC$ is radius and $CP$ is tangent.

$\Rightarrow \angle OCP = {90^ \circ }$

Here $\angle ABC = {90^ \circ }$ because the angle in a semi – circle is a right angle.

$\Rightarrow \angle PCB = \angle PCA - \angle ACB$

$\Rightarrow \angle PCB = {110^ \circ } - {90^ \circ }$

$\Rightarrow \angle PCB = {20^ \circ }$ 

Therefore, $\angle OCB$ is given as,

$\Rightarrow \angle OCB = \angle OCP - \angle PCB$

$\Rightarrow \angle OCB = {90^ \circ } - {20^ \circ }$

$\Rightarrow \angle OCB = {70^ \circ }$ 

Now, in a triangle $OBC$, $OB = OC$ because they are the radius of the circle.

$\Rightarrow \angle OBC = \angle OCB$

$\Rightarrow \angle OBC = {70^ \circ }$ 

Since, $\angle OBC$ and $\angle CBA$ are the same, hence $\angle CBA = {70^ \circ }$.

13. If an isosceles triangle $ABC$, in which $AB = AC = 6 cm$, inscribed in a circle of radius $9 cm$, find the area of the triangle.

Ans:

In the above figure $OA$ is joined intersecting the side $BC$ at $M$. The altitude of an isosceles triangle passes through the centre of the circle, so $AM$ is the altitude of the triangle. Therefore, $AM$ is perpendicular to $BC$.

$BC$ can be considered as the chord of the circle and perpendicular from the centre of the circle to a chord bisects it.

$\Rightarrow BM = CM = \dfrac{1}{2}BC$ … (1)

In right triangle $AMC$ using Pythagoras theorem,

$\Rightarrow A{M^2} = A{C^2} - C{M^2}$

$\Rightarrow A{M^2} = {6^2} - C{M^2}$ … (2)

In right triangle $OMC$ using Pythagoras theorem,

$\Rightarrow O{M^2} = O{C^2} - C{M^2}$

$\Rightarrow {\left( {OA - AM} \right)^2} = {9^2} - C{M^2}$

$\Rightarrow O{A^2} + A{M^2} - 2OA.AM = {9^2} - C{M^2}$ 

Using relation (2),

$\Rightarrow {9^2} + {6^2} - C{M^2} - 18AM = {9^2} - C{M^2}$

$\Rightarrow 18AM = 36$

$\Rightarrow AM = 2{\text{ cm}}$ 

Substituting the value of $AM$ in relation (2),

$\Rightarrow {2^2} = {6^2} - C{M^2}$

$\Rightarrow C{M^2} = 32$

$\Rightarrow CM = 4\sqrt 2 {\text{ cm}}$ 

Using relation (1),

$\Rightarrow BC = 2CM$

$\Rightarrow BC = 8\sqrt 2 {\text{ cm}}$ 

Therefore, the area of the triangle $ABC$ is $\dfrac{1}{2} \times base \times height$.

$\Rightarrow$ Area $= \dfrac{1}{2} \times BC \times AM$

$\Rightarrow$ Area $= \dfrac{1}{2} \times 8\sqrt 2  \times 2$

$\Rightarrow$ Area $= 8\sqrt 2 {\text{ c}}{{\text{m}}^2}$

14. A is a point at a distance $13 cm$ from the centre $O$ of a circle of radius $5 cm$. $AP$ and $AQ$ are the tangents to the circle at $P$ and $Q$. If a tangent $BC$ is drawn at a point $R$ lying on the minor arc $PQ$ to intersect $AP$ at $B$ and $AQ$ at $C$, find the perimeter of the $\Delta ABC$.

Ans: The diagram of the given conditions can be shown below: -

The perimeter of the triangle $ABC$ (say $P$) is,

$\Rightarrow P = AB + BC + AC$

$\Rightarrow P = \left( {AP - BP} \right) + \left( {BR + RC} \right) + \left( {AQ - QC} \right)$ 

The tangents drawn from an external point are equal in length, so $BP = BR$, $QC = RC$ and $AP = AQ$.

$\Rightarrow P = \left( {AP - BR} \right) + \left( {BR + RC} \right) + \left( {AP - BC} \right)$

$\Rightarrow P = 2AP$ 

In triangle $OPA$, $OP$ is perpendicular to $AP$ because the radius is perpendicular to the tangent at the point of contact. So, using the Pythagoras theorem.

$\Rightarrow A{P^2} = O{A^2} - O{P^2}$

$\Rightarrow AP = \sqrt {{{\left( {13} \right)}^2} - {{\left( 5 \right)}^2}}$

$\Rightarrow AP = 12{\text{ cm}}$ 

Substituting the value of $AP$ in the perimeter,

$\Rightarrow P = 2 \times 12$

$\Rightarrow P = 24{\text{ cm}}$ 

NCERT Exemplar Solutions Class 10 Maths Chapter 9 – Circles

We at Vedantu provide the students with the NCERT Exemplar Class 10 Maths Chapter 9 Circles, to download the PDF format for free and prepare for the CBSE exams. The NCERT Exemplars problems and solutions have been designed by the experts in accordance with the latest CBSE curriculum for 2024-25. With these solved questions the students will be able to clear their doubts and find detailed answers for all the chapter questions.

In the Circle’s chapter, the students will learn about topics like tangent and its existence in a circle. They will also come across several other examples and activities in the chapter which have to be understood and practiced. So, to facilitate easy learning and help the students grasp all the concepts of circles properly, the free NCERT exemplar for Chapter 9 of Class 10 Maths is available on Vedantu’s site. 

Importance of NCERT Exemplar

The NCERT Exemplars are not just useful for board exams  but also for all the competitive exam preparations at a higher level. Some of the importance of the NCERT Exemplar books are given below:

1. As all NCERT Exemplar books are written by experts after extensive research on topics it provides the students with credible information. The information in the Exemplar is completely authentic and will guide the students in the right direction.

2. The NCERT Exemplar books cover all the basics and fundamentals on all topics for the students apart from the added information of a higher level to provide them with a clear and strong basic understanding.

3. All the NCERT books contain standard questions plus some extra information for benefits to effectively cover the syllabus of the exam.

4. Many questions in JEE-Mains are sometimes directly taken from the NCERT books. 

5. The NCERT Exemplar books have been written in easy language by the experts and involve years of thorough research. 

6. It is important to practice as much as possible for competitive exams and the NCERT Exemplar offers many problems to practice for the students. Thus, practicing NCERT Exemplar problems will give the students an easy hand at twisted questions also. 

Follow the NCERT Class 10 Maths syllabus and complete all the chapters accordingly. Download the solution file for Chapter 9 from Vedantu and proceed to learn how to approach the specific problems that are approached by the experts. Practice using these methods and save time. Develop a strategy to answer all the questions during the board exam and score better than your Class. 

Significance of NCERT Exemplar Solutions for Class 10 Maths Circles

As mentioned earlier, this chapter holds immense importance in the development of concepts related to circles and their geometric elements among the students. They will learn what a circle is and its associated parts such as the radius, diameter, circumference, angles, tangents, chords, etc.

To make this chapter easier to learn, students will need the guidance of the NCERT Exemplar solutions. These solutions will guide students to understand how the definitions, concepts and formulas related to circles are used to solve fundamental problems.

These solutions have been framed by following the latest CBSE syllabus so that students can relate to the topics and formulas explained in the chapter. Hence, it will become a lot easier to formulate the answers to the exemplar questions of this chapter and proceed with the preparation.

The answers in the solutions have been framed in a simpler tone by following the CBSE standards to offer an easier platform. This platform will help students to comprehend problems and learn how to solve them by using specific formulas in the right way.

Hence, the NCERT Exemplar solutions will come in very handy during the practice sessions with the NCERT Exemplar textbook.

Benefits of CBSE Class 10 Circles NCERT Exemplar Solutions

• The problems enlisted in this book focus on training how to use the formulas and concepts of this chapter. Hence, the solutions will make it easier for you.

• Once you are done with the chapter, you can proceed to solve these problems. The simpler solutions given by the experts for the NCERT Exemplar exercises will help you focus on understanding the easiest methods to solve the problems.

• Resolve doubts related to these exercises by using the solutions. Clarify your queries quicker and take your preparation to the next level.

• Learn from the experts how to approach solving such problems. Check the stepwise methods composed by the experts for individual questions and practice. Develop your answering skills by practising more and ace the exams.