




How Zeroes of a Polynomial Appear on a Graph
Expression consists of variables, coefficients, and arithmetic operations. An expression may consist of more than one variable, and the variable's power is any real number.
Let’s understand polynomials definition with example; a polynomial is an expression of one variable. The power of variables of a polynomial must be a natural number. A polynomial represented by P(x), where x is the variable of the polynomial. For example P(x) = \[2x^3+5x+3\].
Degree of a Polynomial
The degree of a polynomial is the highest power of the variable of the polynomial. The degree of linear polynomials is 1 because the highest degree of the polynomial is 1. The degree of a quadratic polynomial is 2 because the highest degree of the polynomial is 2. The degree of a cubic polynomial is 3 because the highest degree of the polynomial is 3.
Types of Polynomials
The type of polynomial depends on the degree of the polynomial.
The general form of a polynomial is \[P(x) = a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_1x+a_{0}\]
Constant polynomial: If \[a_{n}=a_{n-1}=\cdots =a_2=a_{1}=0\] and \[a_{0}\ne 0\], then the polynomial is known as a constant polynomial. For example: P(x) =3.
Zero polynomial: If \[a_{n}=a_{n-1}=\cdots =a_2=a_{1}=a_{0}= 0\], then the polynomial is known as a zero polynomial.
Linear polynomial: If \[a_{n}=a_{n-1} = a_2 = 0\] and \[a_{1}\ne 0\], then the polynomial is known as linear polynomial.
Quadratic polynomial: If \[a_{n}=a_{n-1} =\cdots =a_3=0\] and \[a_{2}\ne 0\], then the polynomial is known as quadratic polynomial.
Cubic polynomial: If \[a_{n}=a_{n-1} =\cdots0= a_4\] and \[a_{3}\ne 0\], then the polynomial is known as quadratic polynomial.
Zeroes of the Polynomial Definition
The zero of a polynomial is the value of the variable for which the value of the polynomial becomes zero.
The polynomial P(x) has a zero at x = a. This means the value of P(x) at x = a is zero that is P(a) = 0.
Assume a polynomial, \[ P(x)=2x+4\]
Now equate P(x) with zero.
P(x) = 0
\[\Rightarrow 2x+4=0\]
\[\Rightarrow 2x=-4\]
\[\Rightarrow x=-2\]
The zero of the polynomial P(x)=2x+4 is x = -2.
Number of Zeros of a Polynomial
The degree of a linear polynomial is 1. Thus the number of zeros of a linear polynomial is at most 1.
The degree of a quadratic polynomial is 2. Thus the number of zeros of a linear polynomial is at most 2.
The degree of a cubic polynomial is 3. Thus the number of zeros of a linear polynomial is at most 3.
How to Obtain the Zero of a Linear Polynomial Geometrically?
The degree of a polynomial is the highest power of the variable of the polynomial. The degree of a linear polynomial is 1. Thus the number of zeros of the polynomial is 1.
To get a zero of linear polynomials geometrically, we will find the point where the given linear polynomial cuts the x-axis. Suppose the polynomial cuts the x-axis at x = a, then the zero of the polynomial is a.
For Example,
Assume an equation of a linear polynomial P(x) = x+4.
The graphical representation of a linear polynomial is shown below:
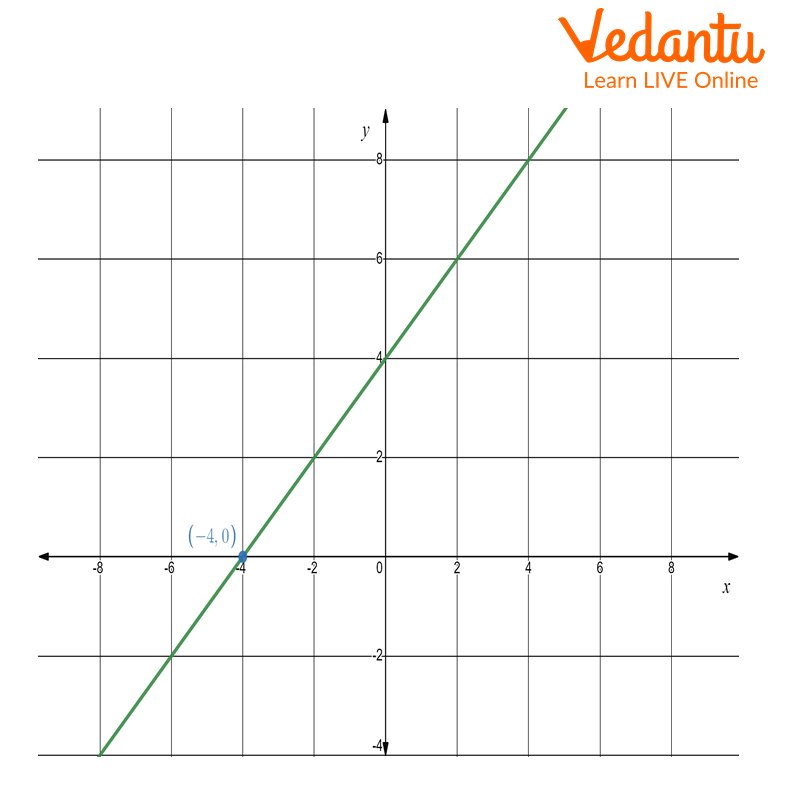
Linear polynomial
The linear polynomial P(x) cuts the x-axis at (-4,0). Thus the zero of the polynomial is -4. It means P(-4) = 0. The zero of the polynomial P(x) = x+4 is -4.
Since the given polynomial is a linear polynomial, thus it intersects the x-axis at a point.
Geometrical Meaning of the Zeros of a Polynomial
The number of zeros of a polynomial is dependent on the degree of that polynomial. The number of zeros of a polynomial is less than or equal to the degree of the polynomial. The number of zeros of a polynomial is equal x-intercepts of the polynomials.
Geometrical Representation of Zeros
The number of zeros is equal to the number of the x-intercept of the polynomial graph. Below we have the geometrical meaning of zeroes of polynomials with examples
Linear polynomial: The number of the x-intercepts is 1. Thus, the number of zeros is 1 for the linear polynomial.
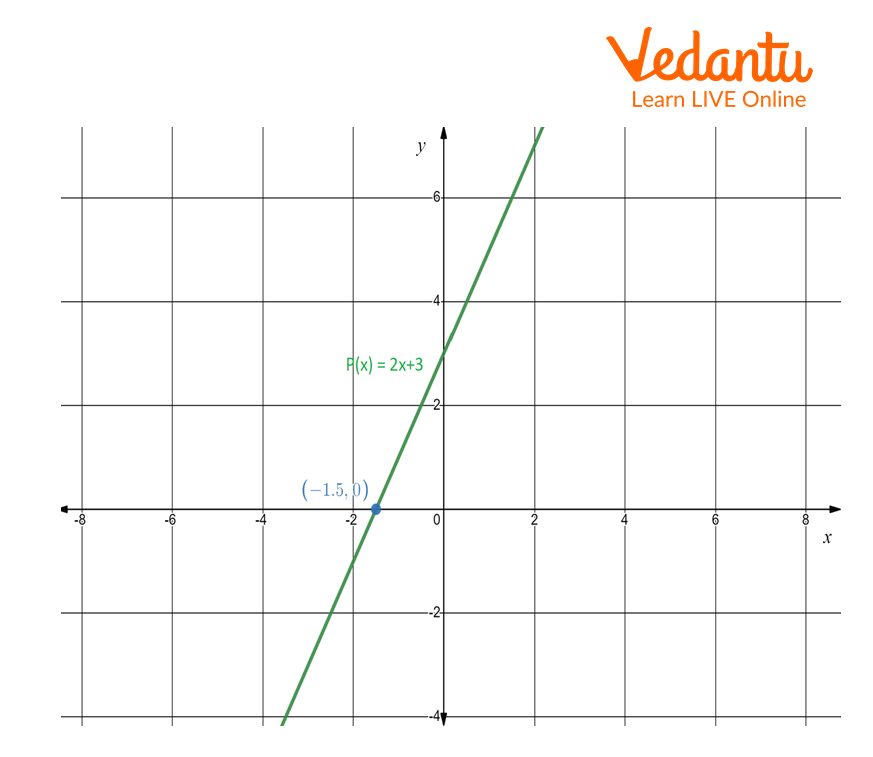
Graph of a linear polynomial
Quadratic polynomial: The quadratic polynomial has at most 2 zeros. Thus, the graph of quadratic polynomial intercepts at two points.
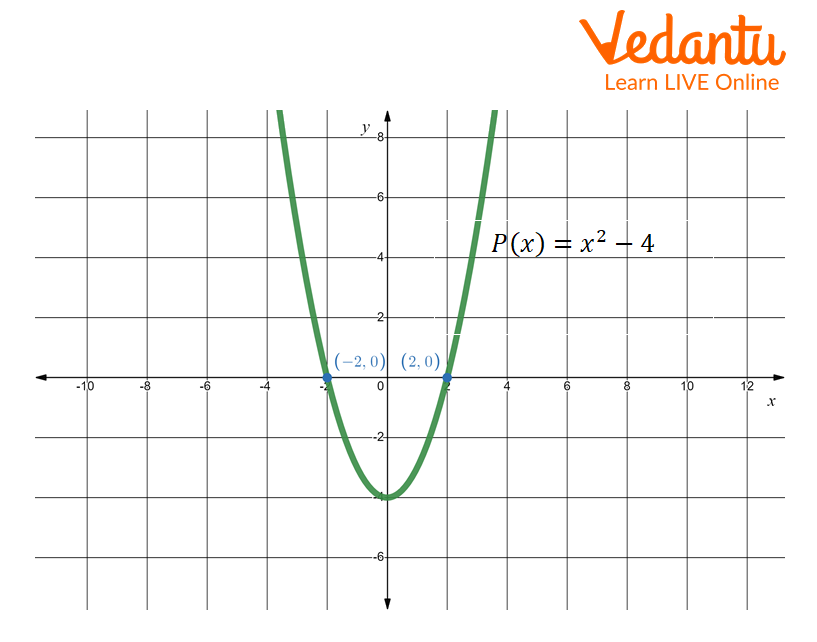
Graph of the quadratic polynomial
Cubic polynomial: The cubic polynomial has at most 3 zeros. Thus, the graph of cubic polynomial intercepts at three points.
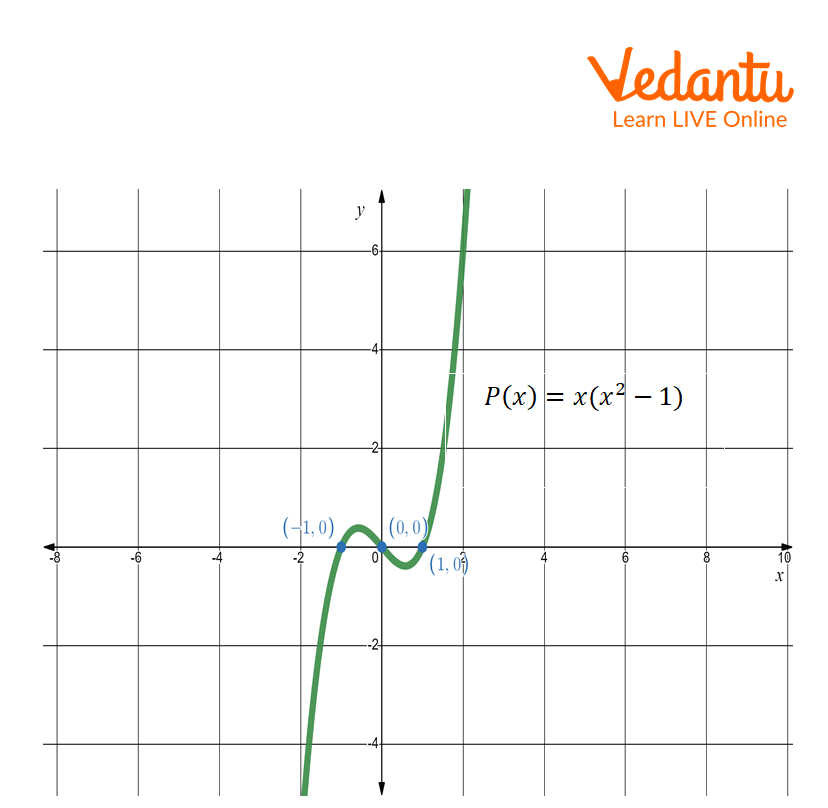
Graph of a cubic polynomial
Solved Problems
Q1 Find the number of zeroes of the polynomial in a given graph.
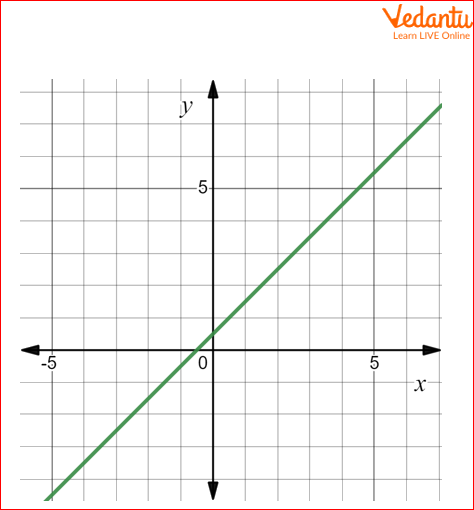
Solution 1: From the above geometrical presentation we can see that the straight line intersects the x-axis at one time, therefore the number of zeros in the given polynomial is one.
Q2 Find the zeros of the polynomial \[P(x) =4x^{2}-16\].
Solution 2: Given polynomial is \[P(x) =4x^{2}-16\].
Equate P(x) with zero:
\[4x^{2}-16=0\]
\[\Rightarrow 4x^{2}=16\]
Divide both sides by 4:
\[\Rightarrow x^{2}=4\]
Take square root both sides
\[\Rightarrow x=\pm 4\]
The zeros of the polynomial are \[\pm 4\].
Q3 Find out the zero of the polynomial y=x+1 geometrically.
Solution3: First we make the table for y=x+1
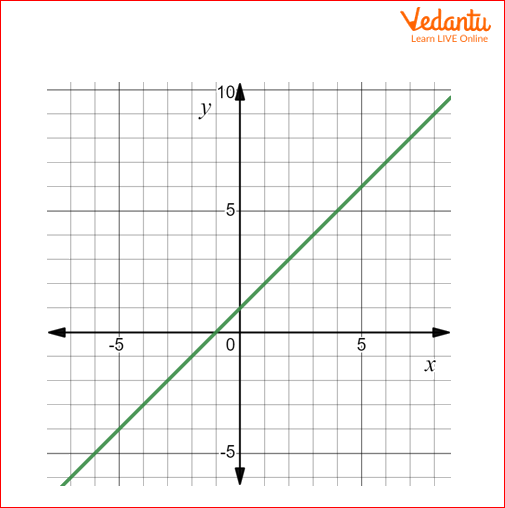
Graph for given table
We can see that at x=-1, given straight line intersecting the x-axis, therefore x=-1 is zero of the given polynomial.
Interesting Facts
If the zeros of a quadratic polynomial are the same, then the graph of the quadratic polynomial touches the x-axis at a point.
If the zeros of a cubic polynomial are the same, then the graph of the cubic polynomial cuts the x-axis at a point.
Summary
The number of zeros of a polynomial depends on the degree of the polynomial. The number of zeros of a polynomial equals the number of x-intercepts of the polynomial. If P(a) = 0, then a is a zero of the polynomial P(x). A linear polynomial has at most 1 zero. A quadratic polynomial has at most 2 zeros and a cubic polynomial has at most 3 zeros.
Practice Problem
Q1 Write the type of the given polynomial (1) 2x+3 (2) \[2x^{2}+3\]
Solution: (1) linear polynomial (2) Quadratic polynomial
Q2 From the given table find the zero of the polynomial.
Solution: The zero is X = 2
FAQs on Geometrical Meaning of Zeroes of the Polynomial
1. What is the geometrical meaning of the zeroes of a polynomial?
The geometrical meaning of the zeroes of a polynomial relates to its graph. The zeroes are the x-coordinates of the points where the graph of the polynomial intersects the x-axis. For a polynomial p(x), if the graph of y = p(x) crosses the x-axis at (k, 0), then 'k' is a zero of the polynomial.
2. How many zeroes does a linear polynomial have geometrically?
A linear polynomial, like p(x) = ax + b (where a ≠ 0), represents a straight line on a graph. Geometrically, a straight line can intersect the x-axis at exactly one point. Therefore, a linear polynomial has exactly one zero. The graph of a constant polynomial, like p(x) = c, is a line parallel to the x-axis and has no zeroes (unless c=0).
3. What does the graph of a quadratic polynomial show about its zeroes?
The graph of a quadratic polynomial, p(x) = ax² + bx + c, is a parabola. The number of zeroes is determined by how this parabola intersects the x-axis. There are three possibilities:
The parabola intersects the x-axis at two distinct points. This means the polynomial has two distinct real zeroes.
The parabola touches the x-axis at exactly one point. This means the polynomial has one real zero (two equal zeroes).
The parabola does not intersect the x-axis at all. This means the polynomial has no real zeroes.
4. Is it possible for the number 0 to be a zero of a polynomial? Explain with an example.
Yes, the number 0 can absolutely be a zero of a polynomial. A zero is any value of the variable that makes the polynomial equal to zero. Consider the polynomial p(x) = x² - 5x. If we substitute x = 0, we get p(0) = (0)² - 5(0) = 0. Geometrically, this means the graph of this polynomial passes through the origin (0,0).
5. What is the difference between the 'zero of a polynomial' and a 'zero polynomial'?
These are two different concepts:
A zero of a polynomial is a specific number (a value of the variable x) that makes the value of the polynomial p(x) equal to zero. For example, for p(x) = x - 4, the zero is 4.
A zero polynomial is the polynomial where all coefficients are zero, written as p(x) = 0. Its graph is the x-axis itself, and every real number is a zero of this polynomial.
6. How many zeroes can a cubic polynomial have based on its graph?
A cubic polynomial can have at most three zeroes. Geometrically, the graph of a cubic polynomial can intersect the x-axis at a maximum of three points. Therefore, a cubic polynomial can have one, two, or three real zeroes, depending on the shape and position of its graph.
7. Why is the degree of a polynomial not always equal to the number of its real zeroes?
The degree of a polynomial indicates the maximum possible number of real zeroes, not the exact number. For example, the quadratic polynomial p(x) = x² + 4 has a degree of 2. However, its graph is a parabola that is entirely above the x-axis and never intersects it. Geometrically, this shows it has zero real zeroes, even though its degree is 2. The zeroes in this case are complex numbers, which are not visible as x-intercepts on the real number plane.
8. What is the key difference between the algebraic and geometrical interpretation of a polynomial's zeroes?
The key difference is the representation:
The algebraic interpretation involves finding a number 'k' such that when you substitute it into the polynomial, the result is zero (i.e., p(k) = 0). It is a computational process.
The geometrical interpretation involves looking at the graph of y = p(x) and finding the x-coordinates of the points where the curve crosses or touches the x-axis. It is a visual process.
Both methods find the same values, which are the zeroes of the polynomial.
9. If a polynomial's graph only touches the x-axis at one point but does not cross it, what does that imply about its zeroes?
If the graph of a polynomial touches the x-axis at a single point (say, x = k) and turns back, it implies that the polynomial has a repeated zero at that point. For example, the quadratic polynomial p(x) = (x - 3)² = x² - 6x + 9 has a graph that touches the x-axis at x = 3. Algebraically, it has two equal zeroes, both of which are 3. This point is also the vertex of the parabola.

















