




What Are Terms and Factors in Mathematical Expressions?
Have you ever thought, about what the terms with the same algebraic factors are called? The term 'factor' is used to express a number as the produt of any two numbers. Factorization is a method for determining factors for any mathematical object, such as a number, a polynomial, or an algebraic expression. Thus, factorization of an algebraic expression refers to the process of identifying the factors of a given algebraic expression. In the given article, children would gain knowledge about the factors of the terms of an expression and the way how to write the factors. Reading this article, students will be able to identify the factors of the terms of the expression. This is the most common topic of algebra, thus should be on the tips of every child to excel in advanced mathematics.
What are the Factors of a Term of an Expression?
The numbers and variables that are multiplied together to form a term are called the factors of the term. For example, 5xyz is a term, whose factors are 5, x, y, and z. Factors can either be positive or negative, but not zero. One cannot further factorize the factors. Generally, factors have a wide application in daily life.
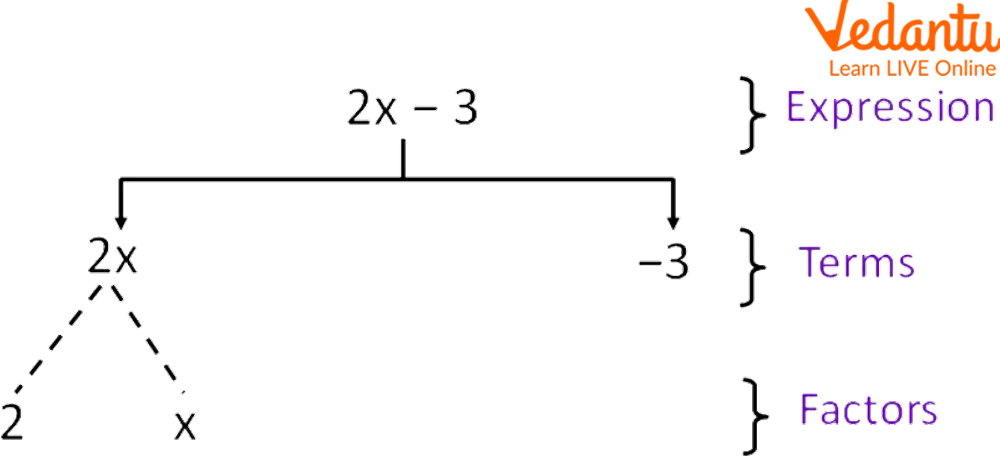
Terms and Factors of an Expression
Factors can be used to divide the entire term by leaving the remainder zero. The factor of the expression is also called the coefficient. The terms with the same algebraic factors are called like terms. For eg: 8y + 3y. While the terms with varied algebraic factors are called, unlike terms. For eg: 2x + 6y.
How to Find Factors?
Steps to find the factors of the term of the expression using the tree diagram are discussed below:
Write the given expression
Separate each term by removing the arithmetical operations and write just below the given expression
Then, factorize the term i.e. writing all the numbers and variables separately
How to Write Factors?
Before we proceed with the topic; of how to write factors, one should be aware of the way to identify the factors of the terms of the expression. The way of writing factors is very simple. Students just need to write all the numbers or variables being written in terms separately by putting commas in between.
Solved Examples
Q 1. Find the factors of the algebraic expression $2+x+x^2$.
Ans: Using a tree diagram,
Write the given expression
$2+x+x^2$
Separate the terms of the given expression, as
$2, x, x^2$
Write corresponding factors to each term of the expression
$2, x, x, x$

Factors of the Given Expression
Q 2. What are the terms and factors in the expression?
15xy – 25y + 18
Ans: Using a tree diagram,
Write the given expression
15xy – 25y + 18
Separate the terms of the given expression, as
15xy, -25y, 18
Write corresponding factors to each term of the expression
15, x, y, -25, y, 18
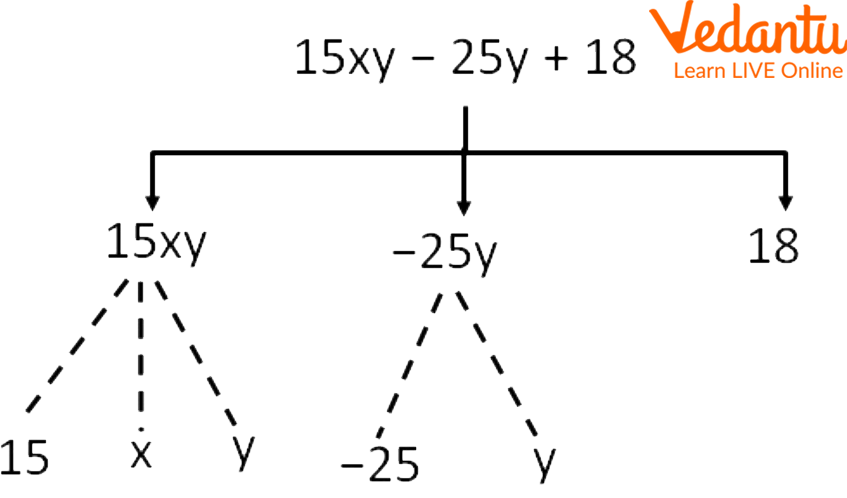
Showing Factors of the Expression, 15xy – 25y + 18
Practice Problems
Q 1. Discover the factors of the number 108.
Ans: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108
Q 2. Identify the factors of the given expression
3x2 - 2
Ans: 3, x, x, -2
Q 3. Identify the terms of the algebraic expression 7x – 9.
Ans: 7x and 9
Q 4. Write the terms in the expression: 9x – 7y + 5 and write the corresponding factors to each term.
Ans: Terms are 9x, -7y, and 5.
Factors are 9, x, -7, y, 5.
Summary
Summing up here with the concept of factors of an expression and the way to find these factors. Every topic in this article has been discussed in a simple language and attractive format for a better understanding of the concepts. Some solved examples are also discussed to make students master the given topics. Practice problems are given above that need to be solved by the students themselves. Hoping you enjoyed reading it. Feel free to ask your doubts by writing in the comments section given below.
FAQs on Terms and Factors of an Expression Explained
1. What is an algebraic expression, as per the CBSE 2025-26 syllabus?
An algebraic expression is a mathematical phrase that combines variables (like x or y), constants (like 5 or -9), and arithmetic operations such as addition, subtraction, multiplication, and division. For example, 4ab - 7c + 2 is an algebraic expression.
2. What are terms and factors in an algebraic expression?
In an algebraic expression, the parts that are separated by addition (+) or subtraction (-) signs are called terms. Each term is made up of a product of its factors. For instance, in the expression 3x² - 5y, the terms are '3x²' and '-5y'. The factors of the term '3x²' are 3, x, and x.
3. How do you identify the coefficient of a term?
The coefficient is the numerical factor of a term. It is the number that is multiplied by the variable(s). For example, in the term 8pq, the coefficient is 8. If a term is just a variable like 'x', its coefficient is understood to be 1, and for '-x', it is -1.
4. How can you represent the terms and factors of an expression using a tree diagram?
A tree diagram provides a visual breakdown of an expression. You start with the expression at the top. The first level of branches splits the expression into its terms. The next level of branches splits each term into its individual factors. For example, for the expression 9xy - 4z, the tree would first branch into terms '9xy' and '-4z'. The '9xy' branch would then split into factors '9', 'x', and 'y'.
5. What are some examples of expressions based on the number of terms?
Expressions are named based on their number of terms:
- Monomial: An expression with a single term (e.g., 7a²).
- Binomial: An expression with two unlike terms (e.g., 2x + 3y).
- Trinomial: An expression with three unlike terms (e.g., p² - 4q + 5r).
6. What is the key difference between a 'term' and a 'factor'?
The primary difference is their relationship within the expression. Terms are the building blocks that are added or subtracted to form an expression. Factors are the numbers or variables that are multiplied together to form a single term. In the expression 6ab + c, '6ab' and 'c' are terms, while '6', 'a', and 'b' are factors of the first term.
7. Why is identifying 'like terms' and 'unlike terms' important?
This distinction is crucial for simplifying expressions. Like terms have the exact same variables raised to the same powers (e.g., 3x² and -2x²). Unlike terms have different variables or exponents (e.g., 3x and 3x²). You can only perform addition and subtraction on like terms to simplify an expression. For example, 3x² + 2x² simplifies to 5x², but 3x + 3x² cannot be simplified further.
8. Does a constant, such as the number 12, have terms and factors?
Yes. In algebra, a standalone constant like 12 is considered a complete expression in itself. It is a monomial, which means it has exactly one term: the term '12'. This term is also referred to as a constant term. Its numerical factors are numbers that divide it evenly (e.g., 1, 2, 3, 4, 6, 12), but in the context of algebraic factors, '12' is treated as a single factor.
9. How do terms and factors apply to real-world formulas, such as the area of a rectangle (l × b)?
In the formula for the area of a rectangle, A = lb, the expression 'lb' is a monomial (a single term). The variables 'l' (length) and 'b' (width) are the factors of this term. This shows how a real-world calculation is represented by an algebraic term formed by the product of its factors.























