




How Does the Zero Polynomial Work in Algebra?
A polynomial is an algebraic phrase with one or more terms, as we are previously aware. The real values of the variable for which the value of the polynomial becomes 0 are known as polynomial zeroes. Therefore, if $p(m) = 0$ and $p(n) = 0$, then the real numbers 'm' and 'n' are zeroes of the polynomial p(x). A polynomial with the value zero (0) is referred to as a zero polynomial. The greatest power of the variable x in the polynomial ${ax}^2+bx+c=0$ is a polynomial's degree. A degree 1 polynomial is referred to as a linear polynomial.
What are Zero Polynomials?
Any real value of x for which the polynomial's value becomes 0 is defined as the polynomial's zero. If p(k) = 0, then a real integer k is the zero of the polynomial p(x).
Geometrical Meaning of the Zero Polynomial
The x-coordinate of the place where the graph intersects the x-axis serves as the polynomial zero. When a polynomial $p(x$) meets the x-axis at the coordinates $(k, 0), k$ is the polynomial's zero.
At most one point, the graph of a linear polynomial crosses the x-axis.
A quadratic polynomial graph can intersect the x-axis up to two times. The graph in this instance has a parabola-like form.
A quadratic polynomial might contain two separate zeros, two equal zeroes, or no zero geometrically.
A cubic polynomial graph can cross the x-axis a maximum of three times. There can be a maximum of three zeros in a cubic polynomial.
An nth-degree polynomial typically crosses the x-axis a maximum of $n$ times. A polynomial of the nth degree can only have n zeroes at most.
Degree of a Polynomial
The degree of a polynomial is determined by the variable term's highest exponential power. Let’s discuss some types of polynomials based on degree:
A linear polynomial is a polynomial with a degree of $1$. $ax + b$, where $a$ and $b$ are real numbers and are not equal $0$. A linear polynomial is $2x + 3$.
A degree two polynomial is referred to as a quadratic polynomial. A quadratic polynomial has the standard form of $ax^2 + bx + c$, where $a, b$, and $c$ are All real numbers, and a not equal zero, $x^2+ 3x + 4$ is an example.
A cubic polynomial is a three-degree polynomial. The formula for standard form is $ax^3+ bx^2+ cx+ d$, where $a, b, c$, and $d$ are all real integers and not equal to zero. An illustration $x^3+ x^2$.
Representing Zero Polynomial on Graph
A graph spanning the coordinate axis can show a polynomial expression of the form $y = f(x)$. On the x-axis is displayed the value of $x$, and on the y-axis is displayed the value of $f(x)$ or $y$. Depending on the degree of the polynomials, the polynomial expression may take the form of a linear expression, quadratic expression, or cubic expression.
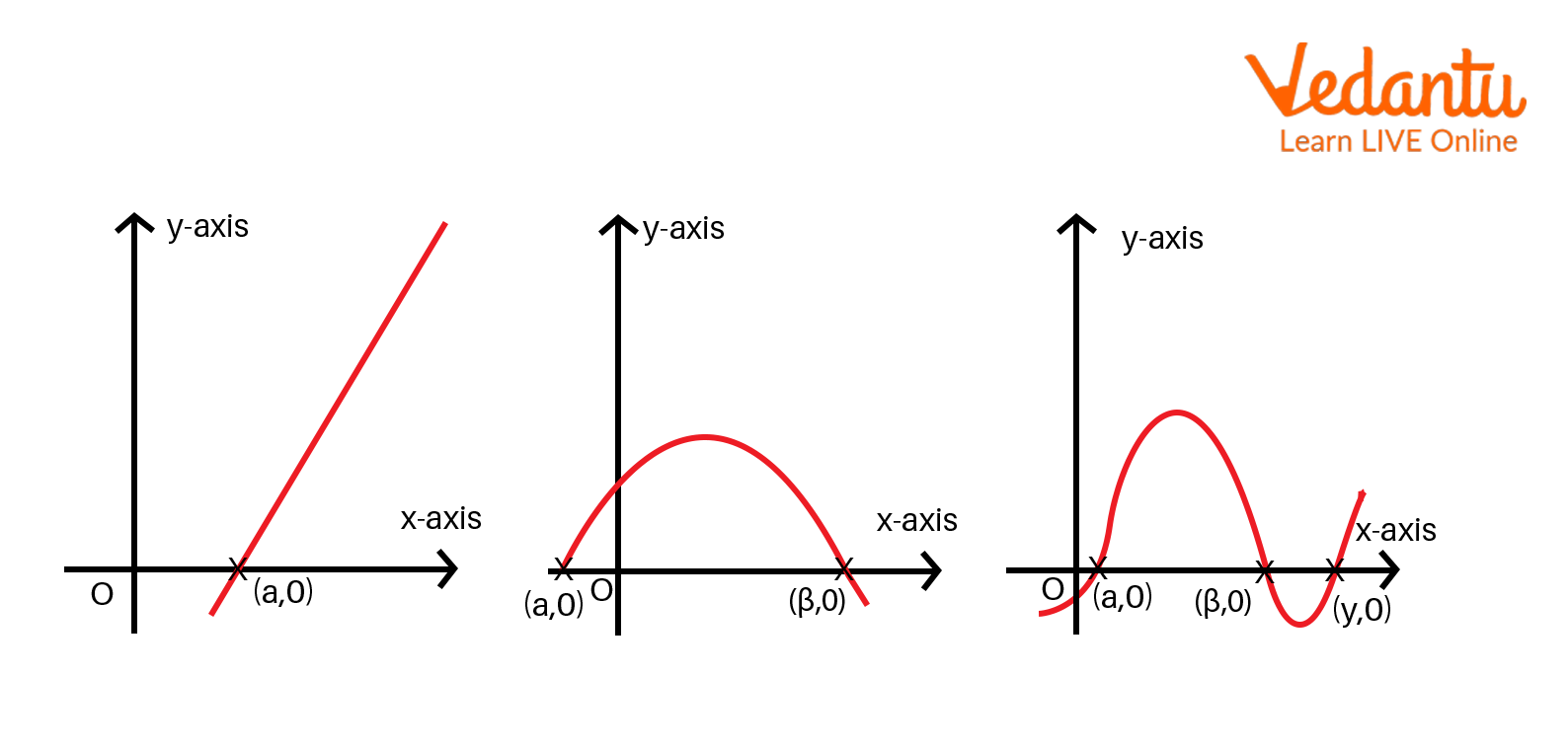
Graph of Zero Polynomial
By looking at the places on the graph where the graph line intersects the x-axis, one can determine a polynomial's zeros.
Solved Examples
Example 1: What is the value of ‘a’ when the degree of the polynomial, $x^3 + x^{a-4} + x^2 + 1$, is $4$?
Solution: The highest power of $x$ in a polynomial $P(x)$ is called the degree $(x)$.
therefore , $x^{a-4} = x^4$
$a-4 = 4, a = 4+4 =8$
Hence, the value of a comes out to be $8$.
Example 2: Sam is aware that a quadratic polynomial has zeros of -3 and 5. How can we assist in deriving the polynomial equation?
Solution: The given zeros of the quadratic polynomial are $-3$ and $5$.
Consider $\alpha = -3$, and $\beta = 5$
Then, calculate the sum of the roots $= α + \beta = 2$
Product of the roots $= \alpha.\beta = -15$
Since, the required quadratic equation is $x^2 - (\alpha + \beta)x + \alpha.\beta = 0$
Put the values of the zeros in the equation above
$ - 2(x) + (-15) = 0$
Hence, $x^2 - 2x - 15 = 0$ is the required equation.
Practice Questions
1. Find the polynomial with the values -2 and -3 for the zeros.
$x^2-5x-6=0$
$x^2+6x+5=0$
$x^2+5x+6=0$
$x^2-5x+6=0$
Answer: C
2. A polynomial's zeros are also known as the equation's____
Variables
Roots
Constants
Answer: D
Summary
Let's review what we learnt from this article. All x-values that reduce a polynomial, p(x), to zero are considered zeros. They are intriguing to us for a variety of reasons, one of which is because they show the graph's x-intercepts for the polynomial. Their relationship to the polynomial factors is direct. This article discussed the geometric meaning of a polynomial's zeros and how to find them. For you to better comprehend this idea, we have included practice problems and examples with answers that have been solved.
FAQs on Zero Polynomial: Meaning, Properties & Practice
1. What is a zero polynomial?
A zero polynomial is a special type of polynomial where all the coefficients of the variables are zero. It is represented as p(x) = 0. Regardless of the value substituted for the variable x, the polynomial's value will always be zero.
2. What is the degree of a zero polynomial and why is it considered 'not defined'?
The degree of a zero polynomial is not defined. This is because the degree of a polynomial is the highest power of the variable with a non-zero coefficient. Since a zero polynomial, like p(x) = 0x² + 0x + 0, has no non-zero coefficients, there is no term from which to determine a highest power, making its degree undefined.
3. What is the key difference between a 'zero polynomial' and the 'zero of a polynomial'?
These two terms refer to very different concepts:
- A zero polynomial is the polynomial function itself, p(x) = 0, where every coefficient is zero.
- A zero of a polynomial (also known as a root) is a specific numerical value of the variable 'x' that makes the value of any polynomial equal to zero. For example, for the polynomial p(x) = x - 5, the zero is 5.
4. Can you provide an example of a zero polynomial?
Yes. A zero polynomial can be written simply as p(x) = 0. In a more expanded form, it could look like p(y) = 0y³ + 0y² + 0y + 0. In both cases, because all coefficients are zero, the expression always equals 0.
5. How does a zero polynomial differ from a non-zero constant polynomial?
The main difference lies in their degree. A zero polynomial (p(x) = 0) has a degree that is not defined. In contrast, a non-zero constant polynomial (e.g., p(x) = 7) is a polynomial where the constant term is not zero, and its degree is 0 because it can be written as p(x) = 7x⁰.
6. What is considered the zero (or root) of a zero polynomial?
The zero of a polynomial is the value of the variable that makes the polynomial equal to zero. For the zero polynomial, p(x) = 0, the equation is satisfied for any real number you substitute for x. Therefore, every real number is a zero of the zero polynomial. As per the CBSE curriculum for class 9, the zero of the zero polynomial is every real number.
7. For any given value of the variable, what is the output of a zero polynomial?
The output of a zero polynomial is always 0. This is its defining characteristic. No matter what number you choose for the variable (e.g., x = 2, x = -10, or x = 100), the result will be zero because each term is multiplied by a coefficient of zero.
8. Does the zero polynomial have any terms?
A zero polynomial has no non-zero terms. While it can be written with terms like 0x² and 0x, these all evaluate to zero. Therefore, it is often simply written as '0', representing a polynomial with no effective terms. This is why its degree is not defined.





































