What is the Perpendicular Line Theorem?

The perpendicular Line Theorem is a fundamental tool of Euclidean Geometry and is used to derive the various properties of perpendicular lines. In this article, we will discuss the proof of the theorem and its importance in geometry. Perpendicular lines are the lines which intersect each other at 90 degrees. So, in this article, we will discuss the properties of such lines and the examples related to the perpendicular line theorem. Here, the theorem will be proved with the help of figures and diagrams.

Statement of Perpendicular Line Theorem

According to the Perpendicular Line Theorem, if two straight lines are intersecting each other at a point and forming a linear pair of equal angles at that point, then the lines are perpendicular to each other.

Proof of Perpendicular Line Theorem

Perpendicular Line Theorem

Let AB and CD be the lines intersecting at point O.

According to the statement of the Perpendicular Lines Theorem,

AB and CD make a pair of equal angles at O.

i.e.,

$\angle 1=\angle 2$

Also, we know from linear pair angles property,

$\angle 1+\angle 2=180^{\circ}$

Putting $\angle 1=\angle 2$, we get

$\therefore \angle 1=\angle 2=\dfrac{180}{2}=90^{\circ}$

Or we can say that lines AB and CD are perpendicular to each other as the angle between them is 90 degrees.

Hence Proved.

Limitations of Perpendicular Line Theorem

• The Perpendicular Line theorem doesn’t state anything if the pair of angles are not equal.

• It does not apply to any other types of line such as parallel lines.

Applications of Perpendicular Line Theorem

• The Perpendicular Line Theorem has a wide range of applications in construction as the walls of buildings are always perpendicular to each other.

• The Perpendicular Line Theorem forms one of the fundamental tools of geometry and helps in solving geometry problems.

Solved Examples

1. In the quadrilateral $A B C D, A C$ and $B D$ make an equal pair of angles and $\angle O A D=30^{\circ}$. Find $\angle A D O$.

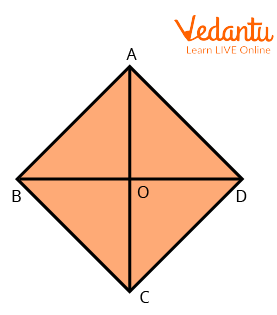
A Quadrilateral ABCD

Ans: Using the perpendicular line theorem,

$\angle A O D=90^{\circ}$

And we know

$\Rightarrow \angle O A D+\angle A O D+\angle A D O=180^{\circ}$

Putting the values we get,

$\Rightarrow 30^{\circ}+90^{\circ}+\angle A D O=180^{\circ} $

$\Rightarrow \angle A D O=180^{\circ}-120^{\circ}$

$\Rightarrow \angle A D O=60^{\circ}$

2. In the quadrilateral $A B C D, A C$ and $B D$ make an equal pair of angles and $\angle O A D=60^{\circ}$. Find $\angle A D O$.

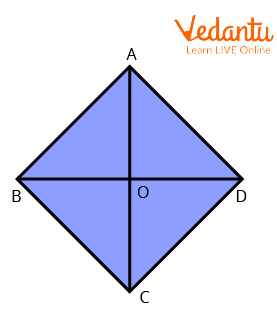
Diagonals of a Quadrilateral

Ans: Using the perpendicular line theorem,

$\angle A O D=90^{\circ}$

And we know

$\Rightarrow \angle O A D+\angle A O D+\angle A D O=180^{\circ}$

Putting the values we get,

$\Rightarrow 60^{\circ}+90^{\circ}+\angle ADO=180^{\circ}$

$\Rightarrow \angle A D O=+180^{\circ}-150^{\circ}$

$\angle A D O=30^{\circ}$

3. In the quadrilateral $A B C D, A C$ and $B D$ make an equal pair of angles and $\angle O C D=45^{\circ}$. Find $\angle C D O$.

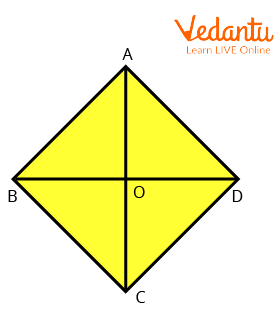
Equal Angles of a Quadrilateral

Ans: Using the perpendicular line theorem,

$\angle C O D=90^{\circ}$

And we know

$\Rightarrow \angle O C D+\angle C O D+\angle C D O=180^{\circ}$

Putting the values we get,

$\Rightarrow 45^{\circ}+90^{\circ}+\angle C D O=180^{\circ} $

$\Rightarrow \angle C D O=180^{\circ}-135^{\circ} $

$\Rightarrow \angle C D O=45^{\circ}$

Important Points to Remember

• Lines making equal pairs of angles at intersections are perpendicular to each other.

• If the angles formed between the lines are 90 degrees, then lines are said to be perpendicular lines.

Important Formulas to Remember

• Two lines $AB$ and $CD$ are perpendicular to each other if the angle between them is $90$ degrees.

Conclusion

In the article, we have discussed the detailed proof of the Perpendicular Line Theorem and its applications. We have observed from the above discussions that the perpendicular line theorem is of great use in geometry and reduces our work in solving problems with its application. In all, we can say that it is a theorem of great significance for us.