Question

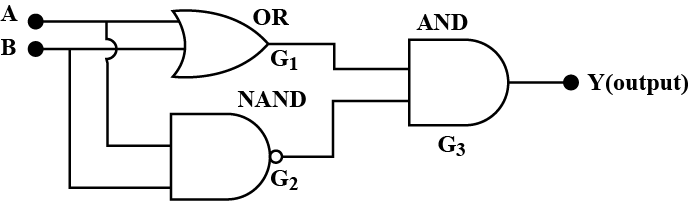
The following logic gate circuit is equivalent to:

(A) NAND gate
(B) OR gate
(C) XOR gate
(D) NOT gate

Answer 1

Hint We know that logic gates are the basic building blocks of any digital system. It is an electronic circuit having one or more than one input and only one output. The relationship between the input and the output is based on a certain logic. Based on this, logic gates are named as AND gate, OR gate, NOT gate etc. There are seven basic logic gates: AND, OR, XOR, NOT, NAND, NOR, and XNOR. The AND gate is so named because, if 0 is called "false" and 1 is called "true," the gate acts in the same way as the logical "and" operator.

Complete step by step answer
We know that a logic gate in a microchip is made up of a specific arrangement of transistors. For modern microchips, the transistors are of the kind called Metal-Oxide-Semiconductor Field-Effect Transistor (MOSFET), and the semiconductor used is silicon. But as we can construct other logic switching functions using just these gates on their own, they are both called a minimal set of gates. Thus, the NAND and the NOR gates are commonly referred to as Universal Logic Gates.
When a transistor is on, or open, then an electric current can flow through. When we string a bunch of these transistors together, then we get what's called a logic gate, which lets us add, subtract, multiply, and divide binary numbers in any way imaginable. In a physical circuit, these logic gates have: Inputs.
$\mathrm{Y}_{1}=\mathrm{A}+\mathrm{B}, \mathrm{Y}_{2}=\overline{\mathrm{A.B}}$
So, we can write that:
$\mathrm{Y}=(\mathrm{A}+\mathrm{B}) \cdot \overline{\mathrm{AB}}=\mathrm{A} \cdot \overline{\mathrm{A}}+\mathrm{A} \cdot \overline{\mathrm{B}}+\mathrm{B} \cdot \overline{\mathrm{A}}+\mathrm{B} \cdot \overline{\mathrm{B}}$
Thus, we get:
$=0+\mathrm{A} \cdot \overline{\mathrm{B}}+\mathrm{B} \cdot \overline{\mathrm{A}}+0=\mathrm{A} \cdot \overline{\mathrm{B}}+\mathrm{B} \cdot \overline{\mathrm{A}}$
This expression is for XOR.

So, the correct answer is option C.

Note We know that digital systems are said to be constructed by using logic gates. These gates are the AND, OR, NOT, NAND, NOR, EXOR and EXNOR gates. The basic operations are described below with the aid of truth tables. AND gate The AND gate is an electronic circuit that gives a high output (1) only if all its inputs are high. Logic gates perform basic logical functions and are the fundamental building blocks of digital integrated circuits. Most logic gates take an input of two binary values, and output a single value of a 1 or 0. Some circuits may have only a few logic gates, while others, such as microprocessors, may have millions of them.