Question

The figure below shows the north and south poles of a permanent magnet in which n turn coil of area of cross-section A is resting, such that for a current i passed through the coil, the plane of the coil makes an angle θ with respect to the direction of magnetic field B . If the plane of the magnetic field and the coil are horizontal and vertical respectively, the torque on the coil will be

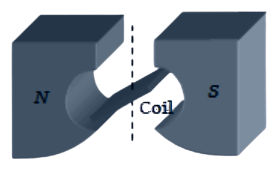
A. τ=niABcosθ
B. τ=niABsinθ
C. τ=niAB
D. None of the above, since the magnetic field is radial

Answer 1

Hint: In this question we will use the concept of torque of a magnetic field and magnetic moment. The term "magnetic moment" refers to the greatest torque a magnet will feel in a single external magnetic field.

Formula used:
The expression of torque is,
\[\tau =MB\operatorname{Sin}({{90}^{\circ }}-\theta )\]
where M=Magnetic Moment, B=Magnetic Field and θ=Angle between plane of coil and magnetic field.

Complete step by step solution:
The torque given by the magnetic field is equal to the product of the magnetic field and the magnetic moment produced by the magnetic field in the direction of the magnetic field.
\[\tau =MB\operatorname{Sin}({{90}^{\circ }}-\theta )\]
Since $\operatorname{Sin}({{90}^{\circ }}-\theta )$ is = Cos(θ)
\[\Rightarrow \tau =MB\operatorname{Cos}(\theta )\]........(1)

Given, number of turns= n, area of cross section= A and current passed= i
For a single coil, the magnetic moment is the product of current flowing through it and the area of the cross section of the coil.
$\Rightarrow M=IA$
For n number of turns, the magnetic moment of one coil is multiplied by n.
$\Rightarrow M=nIA$ - (2)
Substituting the equation (2) in equation (1), we get
$\therefore M=(nIA) B Cos(θ)$

Hence, the correct answer is A.

Additional Information: Torque, which is the cross product of the magnetic moment and the field vector, is experienced by a current-carrying coil maintained in a magnetic field. As a result, the torque is zero when the dipole moment is parallel to the field and maximal when it is perpendicular to the field. Torque on a loop carrying current can be found using τ=NIABsinθ. Maximum torque occurs when θ=90$^\circ$ and sinθ=1.

Note: The component of the direction of the coil taken should be along the magnetic field that is $\operatorname{Sin}({{90}^{\circ }}-\theta )$. And $\operatorname{Sin}({{90}^{\circ }}-\theta )$ should be converted to $\operatorname{Cos}(\theta )$.