Question

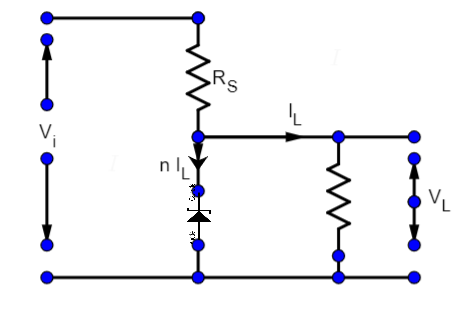
The value of the resistor, $R_S$, needed in the DC voltage regulator circuit shown here, equals:
                             

(A) \[\dfrac{{{V_i} + {V_L}}}{{(n + 1){I_L}}}\]
(B) \[\dfrac{{{V_i} - {V_L}}}{{n{I_L}}}\]
(C) \[\dfrac{{{V_i} + {V_L}}}{{n{I_L}}}\]
(D) \[\dfrac{{{V_i} - {V_L}}}{{(n + 1){I_L}}}\]

Answer 1

Hint: We have to use Kirchhoff’s loop Law to calculate the value of the resistor \[{R_S}\] . For this we will use the formula \[{V_i} - {V_L} = I{R_S}\] , where \[{V_i}\] is input voltage and \[{V_L}\] is output voltage.
As we can see in figure the current I break down into two currents i.e. \[n{I_L},{I_L}\] . So, we substitute these two values in the above equation.
After the substitution we will take the equation from both sides and find the value of \[{R_S}\].

Complete step by step solution
The given circuit is a zener diode circuit which is used as a voltage regulator. In this circuit \[{V_i}\] is unregulated input voltage and \[{V_L}\] is regulated output voltage.
Now value of the resistor is calculated i.e. \[{R_S}\] . For this we will use Kirchhoff's loop Law which states that the algebraic sum of all the potential differences along a closed loop in a circuit is zero.
So, the kirchhoff’s equation for the loop will be:
 \[{V_i} - {V_L} = I{R_S}\] ,as voltage is equal to current \[ \times \]resistance.
Where current, \[I = n{I_L} + {I_L}\] , as current I is broken into \[n{I_L},{I_L}\] .
So the equation is \[{V_i} - {V_L} = (n{I_L} + {I_L}){R_S}\]
By the above equation we can find \[{R_S}\]
 \[{R_S} = \dfrac{{{V_i} - {V_L}}}{{(n{I_L} + {I_L})}}\]
Now if we take \[{I_L}\] common from the denominator in the above equation, then:
 \[{R_S} = \dfrac{{{V_i} - {V_L}}}{{(n + 1){I_L}}}\] .

So, option D is the correct option.

Note: The loop laws directly follow the fact that electrostatic force is a conservative force and the word done by it in any closed loop is zero.
While using Kirchhoff’s law also make sure that the positive negative sign is taken correctly, if it goes wrong the answer will be wrong.
Components are connected together in Series if the same current value flows throughout all the components. Components are connected together in Parallel if they have the same voltage across them.