Question

What is the nature of the graph between the separation of the slits and fringe width in case of young’s double slit experiment ?
A) Straight line with negative slope.
B) Straight line with positive slope.
C) Rectangular hyperbola
D) None of these

Answer 1

Hint: Young’s double slit experiment is a demonstration that light and matter can display characteristics of both classically defined waves and particles. he observed that as the difference /distance between the slits is decreased the fringe width obtained has more width, he concluded that both have inverse relationship as \[fringe\;width(\beta ) \propto \dfrac{1}{{separation\;between\;slits}}\]and when he plotted the data collected this was resembling a shape called rectangular hyperbola.
Complete step by step solution:
We know that the fringe width (\[\beta \]) in case of young’s double slit experiment is given by \[fringe\;width(\beta ) = \lambda \dfrac{D}{d}\] ,
From this equation we conclude that,
\[fringe\;width(\beta ) \propto \dfrac{1}{{separation\;between\;slits}}\]
\[fringe\;width(\beta ) \propto \dfrac{1}{d}\] ; separation between the slits = d.
It means that ;
\[ \Rightarrow \beta d = \]constant.
As we know the graph of \[xy = \]constant is a rectangular hyperbola. Here is the graph between the fringe-width and the separation between slits in Young's double slit experiment.


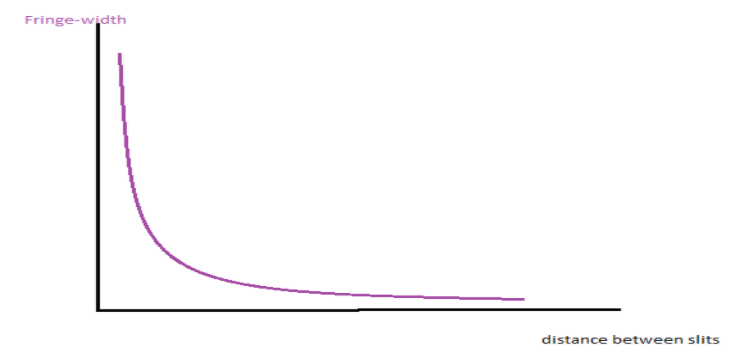
Hence option (C) is the correct answer.

Historically, Young's double slit experiment was first carried out by Young in 1801. This experiment demonstrated that light was a wave.
Young’s double slit experiment uses two coherent sources of light placed at a small distance apart, usually only a few orders of magnitude greater than the wavelength of light is used. Young’s double-slit experiment helped in understanding the wave theory of light which was proposed by Huygens .

Note: The double slit experiment was later conducted using electrons, and the pattern which generated was similar as expected with light. This surprised the world and it changed our understanding of matter and particles, forcing us to accept that matter like light also behaves like a wave.