Question

In the given circuit diagram when the current reaches a steady-state in the circuit, the charge on the capacity of capacitance $C$ will be:
$\left( a \right)$ $CE\dfrac{{{r_1}}}{{\left( {{r_1} + r} \right)}}$
$\left( b \right)$ $CE$
$\left( c \right)$ $CE\dfrac{{{r_1}}}{{\left( {{r_2} + r} \right)}}$
$\left( d \right)$ $CE\dfrac{{{r_2}}}{{\left( {r + {r_2}} \right)}}$

Answer 1

Hint So firstly to know the charge we have to first know the potential difference across the two points. And to know the potential difference we have to first know the currents flow in the circuit in the steady-state. And we know a steady-state capacitor behaves as an open circuit. So by using all this we can find the charge on the capacitance.
Formula:
Charge,
$Q = CV$
Here,
$Q$, will be the charge
$C$, will be the capacitance
$V$, will be the potential difference

Complete Step by Step Solution As we know at a steady-state the capacitor behaves as an open circuit. That means it will produce an infinite resistance to the path of the current and it can be replaced by an open circuit.

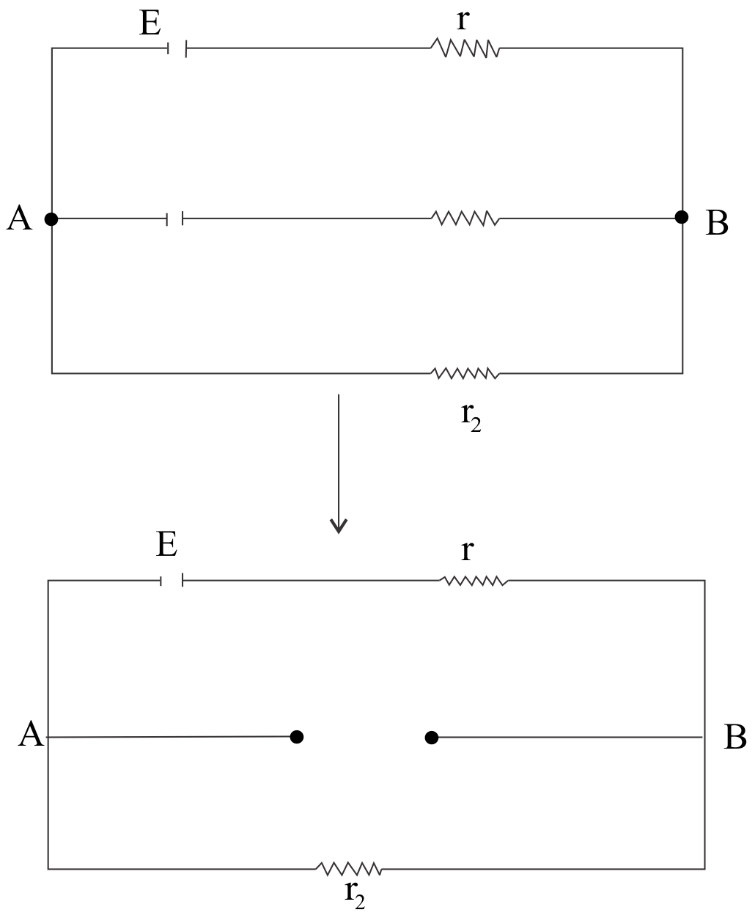
Since it is an open circuit so there will be no use${r_1}$.
By using the current formula,
$i = \dfrac{v}{r}$
Since the total potential difference across the entire circuit is $E$ and the total resistance will be${r_1} + {r_2}$, as they are in series.
Therefore, mathematically it can be written as
$ \Rightarrow i = \dfrac{E}{{{r_1} + {r_2}}}$
So now we have to find the potential difference. By applying Kirchhoff’s law, we will able to get the potential difference across the ${P_2}$
Therefore,
$ \Rightarrow V = i{r_2}$
Now we will put the value of $i$ which we had calculated earlier, we get
$ \Rightarrow V = \dfrac{{E{r_2}}}{{r + {r_2}}}$
Therefore the charge stored on the capacitor will be
As we know,
$Q = CV$
Now substituting the values of $V$, we get
$ \Rightarrow Q = CE\dfrac{{{r_2}}}{{r + {r_2}}}$

Therefore, the option $D$ is the correct choice.

Note The two laws are which helps to determine the current and potential difference in the circuit are:
Current law or junction law - junction is any purpose within the circuit wherever the current will split. Statement: the algebraically total of electrical current at any junction is often adequate zero.
 Voltage law loop theorem- in an exceedingly closed-loop system of electrical network the algebraically total of potential variations for all elements and the algebraically total of all voltage is adequate zero.