Question

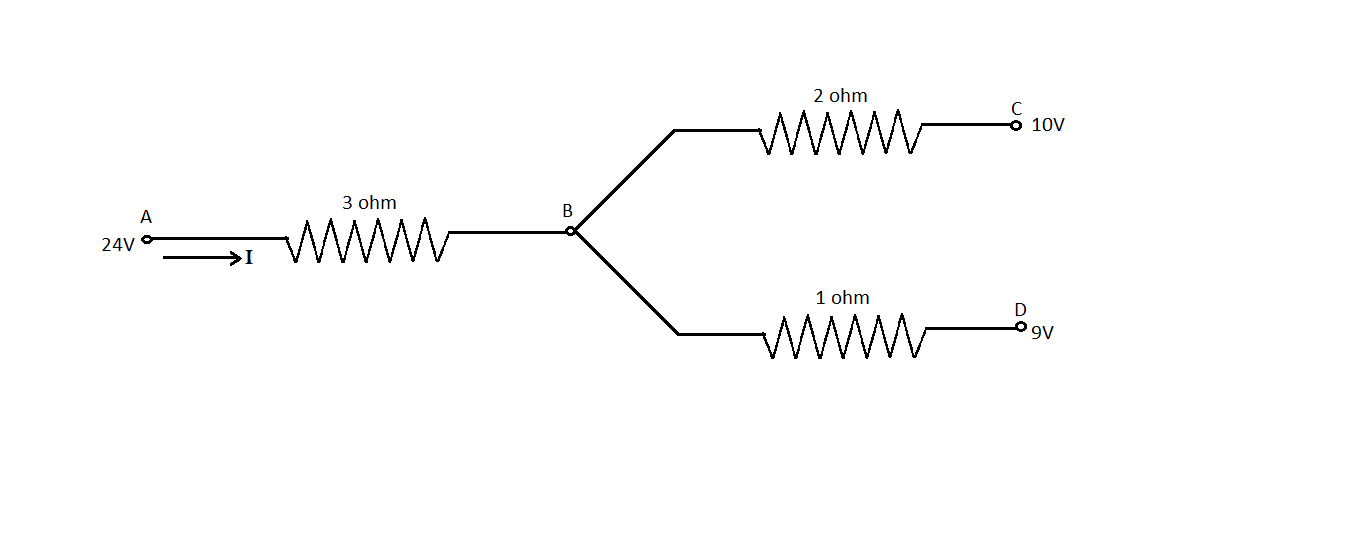
In the circuit shown in the figure, the current $I$ is
A) 6 A
B) 2 A
C) 4 A
D) 7 A

Answer 1

Hint: Use Kirchhoff’s junction rule. Kirchhoff’s junction rule says that the total current into a junction equals the total current out of the junction. A junction is the Intersection of three or more pathways in a circuit. This is also called Kirchhoff’s first law.

Complete step by step solution:
Step 1: In the figure, we can see clearly that the current flowing through the 3-ohm resistor is further divided into two branches. Therefore by Kirchhoff’s law, the current flowing through the 3-ohm resistor will be equal to the sum of the current flowing through 1 ohm and 2-ohm resistors. Therefore we can write
${I_{AB}} = {I_{BC}} + {I_{BD}}$
Step 2: We know that the current flowing through a resistor when a potential difference \[V\] is applied is $I = \dfrac{V}{R}$ . Now if we suppose that the potential at point B is $V$ then we can write
$\therefore \dfrac{{24 - V}}{3} = \dfrac{{V - 10}}{2} + \dfrac{{V - 9}}{1}$
Step 3: Now add the two terms on the right-hand side
$\therefore \dfrac{{24 - V}}{3} = \dfrac{{V - 10 + 2V - 18}}{2}$
$ \Rightarrow \dfrac{{24 - V}}{3} = \dfrac{{3V - 28}}{2}$
Step 4: simplify the above equation and find the value of $V$
$\therefore 48 - 2V = 9V - 84$
$ \Rightarrow 11V = 48 + 84$
$ \Rightarrow 11V = 132$
$ \Rightarrow V = 12volt$
Step 5: Now we know the potential at point B which is 12V therefore we can calculate the current $I$
${I_{AB}} = \dfrac{{\Delta V}}{{{R_{AB}}}}$ , where $\Delta V = 24 - 12$ is the potential difference between points A and B and ${R_{AB}} = 3\Omega $ is the resistor between points A and B.
$\therefore {I_{AB}} = \dfrac{{24 - 12}}{3}$
$ \Rightarrow {I_{AB}} = \dfrac{{12}}{3}$
$ \Rightarrow {I_{AB}} = 4$
Therefore the current flowing through the resistor $3\Omega $ is 4 A.

Hence the option C is correct.

Note: We can confirm whether Kirchhoff’s law is used correctly or not. We do so by adding the amount of current entering the junction and the amount of current leaving the junction. If the summation is zero then our answer is correct. Since we know the potential at point B therefore we can also calculate the current flowing through the remaining two resistors in the circuit. The current flowing through $2\Omega $ the resistor will be ${I_{BC}} = \dfrac{{10 - 12}}{2} = - 1$ and the current flowing through $1\Omega $ the resistor will be ${I_{BD}} = \dfrac{{9 - 12}}{1} = - 3$ . Here we see that ${I_{AB}} + {I_{BC}} + {I_{BD}} = 4 - 1 - 3 = 0$ . Thus the law is confirmed.