
If the vertices of a triangle area unit (2, −2), (−1, −1), and (5,2) then the equation of its circumcircle is?
A) \[\begin{array}{*{20}{c}}
{{x^2} + {y^2} + 3x + 3y + 8}& = &0
\end{array}\]
B) \[\begin{array}{*{20}{c}}
{{x^2} + {y^2} - 3x - 3y - 8}& = &0
\end{array}\]
C) \[\begin{array}{*{20}{c}}
{{x^2} + {y^2} - 3x + 3y + 8}& = &0
\end{array}\]
D) None of these
Answer
240.3k+ views
Hint: First determine the center of the circumcircle and then find the radius of the circumcircle. After getting all these values, apply the equation of the circle.
Formula Used: \[\begin{array}{*{20}{c}}
d& = &{\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} }
\end{array}\]
Complete step by step solution: In this problem, we have given that the vertices of the triangle are (2, −2), (−1, −1), and (5,2) respectively.
Let us assume that the center of the circumcircle is O \[\left( {{x_0},{y_0}} \right)\]and the radius of the circumcircle is R. Now, we will draw a figure according to the given data. Therefore,
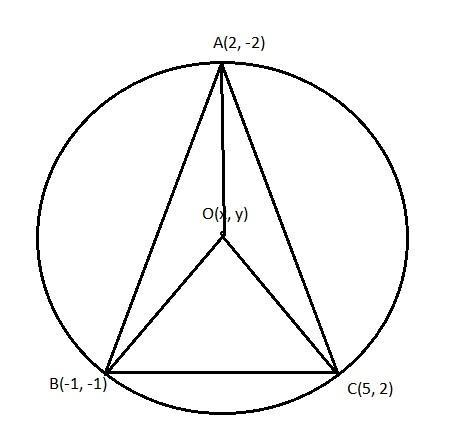
Figure 1
Now according to the figure that we have drawn,
\[ \Rightarrow OA = OB = OC = R\]
To determine the center of the circumcircle, we will write,
\[ \Rightarrow \begin{array}{*{20}{c}}
{OA}& = &{OB}
\end{array}\] ………. (1)
And we know that the formula of the length of the line is,
\[ \Rightarrow \begin{array}{*{20}{c}}
d& = &{\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} }
\end{array}\]
Therefore, The length of the OA,
\[ \Rightarrow \begin{array}{*{20}{c}}
{OA}& = &{\sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }
\end{array}\]
And OB will be,
\[ \Rightarrow \begin{array}{*{20}{c}}
{OB}& = &{\sqrt {{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}} }
\end{array}\]
Now from equation (1). We will get
\[ \Rightarrow \begin{array}{*{20}{c}}
{\sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }& = &{\sqrt {{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}} }
\end{array}\]
Square both sides, we will get
\[ \Rightarrow \begin{array}{*{20}{c}}
{{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}}& = &{{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow 3{x_0} - {y_0}}& = &3
\end{array}\] …………. (A).
Similarly,
For OA and OC, so we will get
\[\begin{array}{*{20}{c}}
{ \Rightarrow OA}& = &{OC}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow \sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }& = &{\sqrt {{{\left( {{x_0} - 5} \right)}^2} + {{\left( {{y_0} - 2} \right)}^2}} }
\end{array}\]
Square both sides we will get
\[\begin{array}{*{20}{c}}
{ \Rightarrow {{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}}& = &{{{\left( {{x_0} - 5} \right)}^2} + {{\left( {{y_0} - 2} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow 6{x_1} + 8{y_1}}& = &{21}
\end{array}\] ……….. (B)
Now from the equation (A) and (B). we will get,
\[\begin{array}{*{20}{c}}
{ \Rightarrow {x_0}}& = &{\dfrac{3}{2}}
\end{array}\] and \[\begin{array}{*{20}{c}}
{{y_0}}& = &{\dfrac{3}{2}}
\end{array}\]
Therefore, the coordinates of the center of the circumcircle are \[\left( {\dfrac{3}{2},\dfrac{3}{2}} \right)\]
Now we will determine the radius of the circumcircle. According to the figure we have,
\[ \Rightarrow OA = OB = OC = R\]
Now
\[\begin{array}{*{20}{c}}
{ \Rightarrow OA}& = &{\sqrt {{{\left( {\dfrac{3}{2} - 2} \right)}^2} + {{\left( {\dfrac{3}{2} + 2} \right)}^2}} }
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow OA}& = &{\dfrac{5}{{\sqrt 2 }}}
\end{array}\]
Now apply the general equation of the circle, we will get
\[\begin{array}{*{20}{c}}
{ \Rightarrow {{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}}& = &{{R^2}}
\end{array}\]
Now put the values,
\[\begin{array}{*{20}{c}}
{ \Rightarrow {{\left( {x - \dfrac{3}{2}} \right)}^2} + {{\left( {y - \dfrac{3}{2}} \right)}^2}}& = &{{{\left( {\dfrac{5}{{\sqrt 2 }}} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow {x^2} + {y^2} - 3x - 3y - 8}& = &0
\end{array}\]
So, Option ‘B’ is correct
Note: It is important to note that the length of the lines OA, OB and OC will be equal (radii of the circle).
Formula Used: \[\begin{array}{*{20}{c}}
d& = &{\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} }
\end{array}\]
Complete step by step solution: In this problem, we have given that the vertices of the triangle are (2, −2), (−1, −1), and (5,2) respectively.
Let us assume that the center of the circumcircle is O \[\left( {{x_0},{y_0}} \right)\]and the radius of the circumcircle is R. Now, we will draw a figure according to the given data. Therefore,

Figure 1
Now according to the figure that we have drawn,
\[ \Rightarrow OA = OB = OC = R\]
To determine the center of the circumcircle, we will write,
\[ \Rightarrow \begin{array}{*{20}{c}}
{OA}& = &{OB}
\end{array}\] ………. (1)
And we know that the formula of the length of the line is,
\[ \Rightarrow \begin{array}{*{20}{c}}
d& = &{\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} }
\end{array}\]
Therefore, The length of the OA,
\[ \Rightarrow \begin{array}{*{20}{c}}
{OA}& = &{\sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }
\end{array}\]
And OB will be,
\[ \Rightarrow \begin{array}{*{20}{c}}
{OB}& = &{\sqrt {{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}} }
\end{array}\]
Now from equation (1). We will get
\[ \Rightarrow \begin{array}{*{20}{c}}
{\sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }& = &{\sqrt {{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}} }
\end{array}\]
Square both sides, we will get
\[ \Rightarrow \begin{array}{*{20}{c}}
{{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}}& = &{{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow 3{x_0} - {y_0}}& = &3
\end{array}\] …………. (A).
Similarly,
For OA and OC, so we will get
\[\begin{array}{*{20}{c}}
{ \Rightarrow OA}& = &{OC}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow \sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }& = &{\sqrt {{{\left( {{x_0} - 5} \right)}^2} + {{\left( {{y_0} - 2} \right)}^2}} }
\end{array}\]
Square both sides we will get
\[\begin{array}{*{20}{c}}
{ \Rightarrow {{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}}& = &{{{\left( {{x_0} - 5} \right)}^2} + {{\left( {{y_0} - 2} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow 6{x_1} + 8{y_1}}& = &{21}
\end{array}\] ……….. (B)
Now from the equation (A) and (B). we will get,
\[\begin{array}{*{20}{c}}
{ \Rightarrow {x_0}}& = &{\dfrac{3}{2}}
\end{array}\] and \[\begin{array}{*{20}{c}}
{{y_0}}& = &{\dfrac{3}{2}}
\end{array}\]
Therefore, the coordinates of the center of the circumcircle are \[\left( {\dfrac{3}{2},\dfrac{3}{2}} \right)\]
Now we will determine the radius of the circumcircle. According to the figure we have,
\[ \Rightarrow OA = OB = OC = R\]
Now
\[\begin{array}{*{20}{c}}
{ \Rightarrow OA}& = &{\sqrt {{{\left( {\dfrac{3}{2} - 2} \right)}^2} + {{\left( {\dfrac{3}{2} + 2} \right)}^2}} }
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow OA}& = &{\dfrac{5}{{\sqrt 2 }}}
\end{array}\]
Now apply the general equation of the circle, we will get
\[\begin{array}{*{20}{c}}
{ \Rightarrow {{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}}& = &{{R^2}}
\end{array}\]
Now put the values,
\[\begin{array}{*{20}{c}}
{ \Rightarrow {{\left( {x - \dfrac{3}{2}} \right)}^2} + {{\left( {y - \dfrac{3}{2}} \right)}^2}}& = &{{{\left( {\dfrac{5}{{\sqrt 2 }}} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow {x^2} + {y^2} - 3x - 3y - 8}& = &0
\end{array}\]
So, Option ‘B’ is correct
Note: It is important to note that the length of the lines OA, OB and OC will be equal (radii of the circle).
Recently Updated Pages
Geometry of Complex Numbers Explained

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Trending doubts
JEE Main 2026: Session 1 Results Out and Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

JEE Main Participating Colleges 2026 - A Complete List of Top Colleges

Clemmensen and Wolff Kishner Reductions Explained for JEE & NEET

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding the Angle of Deviation in a Prism

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

Inductive Effect and Its Role in Acidic Strength

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Electric Field of a Uniformly Charged Ring

Understanding Average and RMS Value in Electrical Circuits




