




Key Differences Between Electrostatic Potential and Capacitance
Electrostatic potential and capacitance are essential concepts in electrostatics, focusing on the behavior of electric charges, their associated energy, and the capacity to store charge. Understanding these principles is fundamental for advanced studies and applications in physics, especially for JEE preparation.
Electrostatic Force and Potential
Electrostatic force describes the interaction between stationary charges. It is governed by Coulomb's law, which establishes the force between two point charges as directly proportional to the product of their charges and inversely proportional to the square of the distance between them.
The mathematical expression for the electrostatic force between two charges $q_1$ and $q_2$ separated by a distance $r$ is given by:
$F=\dfrac{1}{4\pi\varepsilon_0} \dfrac{q_1 q_2}{r^2}$
Here, $\varepsilon_0$ is the permittivity of free space, and the constant $\dfrac{1}{4\pi\varepsilon_0}$ is approximately $9 \times 10^9~\text{Nm}^2\text{C}^{-2}$.
Definition of Electrostatic Potential
Electrostatic potential at a point is defined as the work done per unit charge by an external agent in bringing a positive test charge from infinity to that point, with no change in kinetic energy. The potential is a scalar quantity measured in volts (joule/coulomb).
Mathematically, the potential $V$ at a point is: $V = \dfrac{W}{q}$, where $W$ is the work done and $q$ is the test charge.
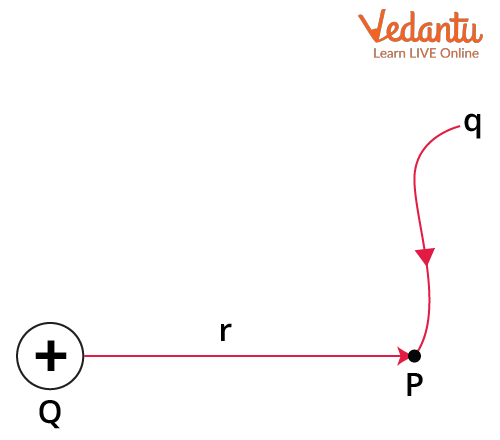
Potential Due to a Point Charge
The electrostatic potential at a distance $r$ from a point charge $Q$ is given by:
$V = \dfrac{1}{4\pi\varepsilon_0} \dfrac{Q}{r}$
This expression shows that the potential decreases with distance from the charge and its sign depends on whether $Q$ is positive or negative. Reference potential is commonly taken as zero at infinity.
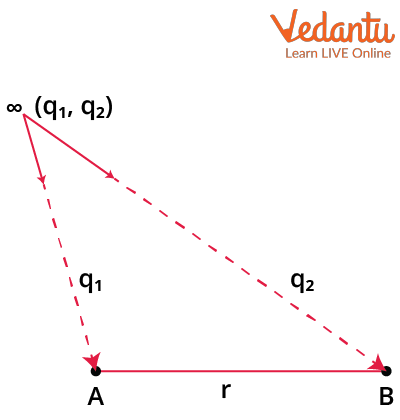
Potential Due to a System of Charges
The total electrostatic potential at a point due to multiple point charges is the algebraic sum of the potentials due to each charge. Using the superposition principle, for charges $q_1, q_2, ..., q_n$ located at different positions, the total potential at point $P$ is:
$V = \dfrac{1}{4\pi\varepsilon_0} \displaystyle\sum_{i=1}^{n} \dfrac{q_i}{r_{i}}$
Potential Due to an Electric Dipole
An electric dipole consists of two equal and opposite charges separated by a distance $2a$. The potential at a point $P$ at distance $r$ and angle $\theta$ from the center of the dipole is:
$V = \dfrac{1}{4\pi\varepsilon_0} \dfrac{p \cos\theta}{r^2}$
where $p=2aq$ is the dipole moment.
Potential Due to Uniformly Charged Bodies
A uniformly charged ring, sphere, or shell produces specific potential distributions. For example, outside a uniformly charged sphere of radius $R$ carrying charge $Q$, at a distance $r \geq R$, the potential is identical to a point charge:
$V = \dfrac{1}{4\pi\varepsilon_0} \dfrac{Q}{r}$
Relation between Electric Field and Potential
The electric field is related to the spatial rate of change of the electric potential. The relationship in one dimension is:
$E = -\dfrac{dV}{dr}$
In three dimensions, the electric field is the negative gradient of the potential:
$\vec{E} = -\nabla V$
Equipotential Surfaces
An equipotential surface is defined as a surface on which every point has the same electric potential. The electric field at every point on an equipotential surface is perpendicular to the surface.
No work is done when moving a charge along an equipotential surface. Two equipotential surfaces can never intersect each other.
To study equipotential surfaces in detail, visit the Equipotential Surface Overview page.
Electrostatic Potential Energy of a System
The electrostatic potential energy of a system is the work required to assemble the system of charges from infinity. For two point charges $q_1$ and $q_2$ separated by a distance $r$, the potential energy $U$ is:
$U = \dfrac{1}{4\pi\varepsilon_0} \dfrac{q_1 q_2}{r}$
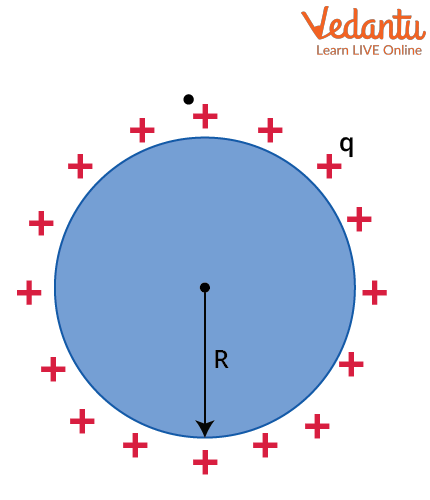
Electrostatics of Conductors and Electrostatic Shielding
Conductors contain free electrons that respond to external electric fields. In electrostatic equilibrium, the electric field inside a conductor is zero. Excess charge resides only on the outer surface, and the conductor's surface forms an equipotential. Electrostatic shielding is achieved by enclosing a region with a conducting shell, making the internal field zero if no charge is inside.
Capacitance and Types of Capacitors
Capacitance is the ability of a system to store electric charge. For a conductor, capacitance $C$ is defined by the relation $C = \dfrac{Q}{V}$, where $Q$ is the charge and $V$ is the potential difference.
For an isolated spherical conductor of radius $R$:
$C = 4\pi\varepsilon_0 R$
Capacitors are commonly designed as parallel plate, spherical, or cylindrical types.
Parallel Plate Capacitor
A parallel plate capacitor consists of two conducting plates of area $A$, separated by distance $d$. Its capacitance in vacuum (or air) is:
$C = \varepsilon_0 \dfrac{A}{d}$
If a dielectric with relative permittivity $\varepsilon_r$ is inserted, capacitance increases by a factor of $\varepsilon_r$:
$C = \varepsilon_0 \varepsilon_r \dfrac{A}{d}$
Combination of Capacitors
Capacitors can be connected in series or parallel arrangements to obtain desired capacitance values. When connected in series, the reciprocal of equivalent capacitance is the sum of reciprocals of individual capacitances. In parallel, the total capacitance is the sum of individual capacitances.
| Combination | Equivalent Capacitance |
|---|---|
| Series ($C_1, C_2,...$) | $\dfrac{1}{C} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + ...$ |
| Parallel ($C_1, C_2,...$) | $C = C_1 + C_2 + ...$ |
Dielectrics and Capacitance
A dielectric is an insulating material placed between the plates of a capacitor, increasing its capacitance. The relative permittivity ($\varepsilon_r$) quantifies how much the dielectric increases the capacitance compared to vacuum. The presence of a dielectric reduces the effective electric field and permits additional charge storage for the same potential difference.
Energy Stored in a Capacitor
A charged capacitor stores energy in its electric field. The total energy stored ($U$) is given by:
$U = \dfrac{1}{2} C V^2 = \dfrac{Q^2}{2C} = \dfrac{1}{2} Q V$
Solved Examples
Example 1: Calculate the potential at a point $0.5$ m from a charge $q = 2.5 \times 10^{-8}$ C.
Solution:
$V = \dfrac{1}{4\pi\varepsilon_0}\dfrac{q}{r} = 9 \times 10^9 \cdot \dfrac{2.5 \times 10^{-8}}{0.5}= 450~\text{V}$
Example 2: A capacitor has stored energy $U = 4.2 \times 10^{20}$ J and capacitance $C = 1.4 \times 10^{-6}$ F. The voltage across the plates is $V = \sqrt{\dfrac{2U}{C}} = \sqrt{\dfrac{2 \times 4.2 \times 10^{20}}{1.4 \times 10^{-6}}} = 2.45 \times 10^{13}$ V.
Key Points on Electrostatic Potential and Capacitance
- Potential is work per unit charge
- Capacitance measures ability to store charge
- Higher dielectric constant increases capacitance
- Energy stored proportional to square of voltage
- Equipotential surfaces are always perpendicular to field lines
Related Concepts and Resources
For thorough understanding, explore topics such as Understanding Electric Potential and related areas. Access extensive notes, important formulas, and practice problems to master electrostatic potential and capacitance for JEE-level examinations.
FAQs on Understanding Electrostatic Potential and Capacitance
1. What is electrostatic potential and how is it defined?
Electrostatic potential at a point refers to the work done by an external force in bringing a unit positive charge from infinity to that point, keeping it stationary with respect to other charges.
- It is measured in volts (V).
- Mathematically, it is given by: V = W/q, where W is work done and q is the charge.
- This concept is fundamental in understanding electric fields and potential energy in physics.
2. What is the difference between electric potential and potential difference?
Electric potential refers to the potential energy per unit charge at a specific point, while potential difference is the difference in electric potential between two points.
- Potential difference determines the direction of current flow.
- Measured in volts (V) for both terms.
- Potential difference drives charge movement in circuits and other systems.
3. What is a capacitor and how does it store charge?
A capacitor is a device used to store electric charge and energy in the electric field between its plates.
- It consists of two conductors separated by an insulator (dielectric).
- When connected to a voltage source, opposite charges accumulate on each plate.
- The ability of a capacitor to store charge is called capacitance (C), measured in farads (F).
4. How is the capacitance of a parallel plate capacitor calculated?
The capacitance of a parallel plate capacitor depends on plate area, separation, and dielectric.
- Formula: C = ε₀εr (A/d)
- ε₀ is the permittivity of free space; εr is the relative permittivity of the dielectric.
- A is plate area, d is plate separation.
- Increasing area or using a better dielectric increases capacitance.
5. What are the uses of capacitors in everyday life and technology?
Capacitors have a wide range of uses in electronics and technology.
- Used for energy storage and release in circuits.
- Help in filtering noise and smoothing signals in power supplies.
- Employed in timing circuits, sensors, and radio tuners.
6. What factors affect the capacitance of a capacitor?
The capacitance is affected by the physical and material properties of the capacitor:
- Area of the plates (A)
- Distance between the plates (d)
- Type and relative permittivity (εr) of the dielectric
- Larger area and higher permittivity increase capacitance, while greater separation decreases it.
7. What is the principle of superposition in electrostatics?
The principle of superposition states that the net electrostatic potential at a point due to multiple charges is the algebraic sum of potentials due to individual charges at that point.
- This allows solving complex charge arrangements easily.
- Key to calculations involving systems of charges in electrostatics.
8. Define equipotential surfaces and state their properties.
Equipotential surfaces are surfaces on which every point has the same electric potential.
- No work is required to move a charge along an equipotential.
- Equipotential surfaces are always perpendicular to electric field lines.
- They help in visualising electric fields and potential distributions.
9. How does introducing a dielectric affect a capacitor's behavior?
Introducing a dielectric material between capacitor plates increases its capacitance by reducing the electric field for a given charge.
- Dielectrics increase charge storage without raising potential difference.
- They lower the risk of dielectric breakdown.
10. What is the energy stored in a charged capacitor and how is it calculated?
The energy stored in a capacitor is the work done to charge it to a given voltage.
- Formula: U = ½CV² where U is energy, C is capacitance, and V is potential difference.
- Measured in joules (J).
- This energy can be quickly released in electronic circuits when needed.
11. What is the SI unit of capacitance?
The SI unit of capacitance is the farad (F).
- One farad is the capacitance when one coulomb of charge raises the potential by one volt.
12. What happens when capacitors are connected in series and in parallel?
Connecting capacitors in series or parallel affects total capacitance.
- In series: 1/Ceq = 1/C1 + 1/C2 + ... (total capacitance decreases)
- In parallel: Ceq = C1 + C2 + ... (total capacitance increases)
- This helps adapt circuits for various applications.
13. State and explain Gauss's law in electrostatics.
Gauss's law states that the total electric flux through a closed surface is equal to 1/ε₀ times the charge enclosed within the surface.
- Mathematically: ∮E•dA = Q/ε₀
- Useful for symmetrical charge distributions like spheres and cylinders.


































