Question

For the $L - $ shaped vessel shown in the figure, determine the value of acceleration $a$ so that the pressure at point $A$ becomes equal to $\dfrac{{{p_0}}}{2}$? (${p_0}$ is atmospheric pressure)

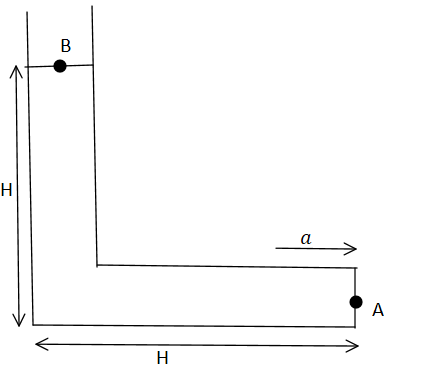
A) $g$
B) $\dfrac{g}{2} + \dfrac{{{p_0}}}{{2\rho H}}$
C) $\dfrac{{{p_0}}}{{2\rho H}} + g$
D) $\dfrac{{3{p_0}}}{{2\rho H}} + g$

Answer 1

Hint: The pressure at which the atmosphere is in directly in contact with the surface is known as atmospheric pressure. Bernoulli’s theorem is based upon the conservation of total energy in a system.

Complete step by step answer:
Bernoulli’s theorem states that the total energy (pressure energy, potential energy and kinetic energy) per unit volume or mass of an incompressible and non-viscous fluid in steady flow through a pipe remains constant throughout the flow, provided there is no source or sink of the fluid along the length of the pipe.
$P + \rho gh + \dfrac{1}{2}\rho {v^2} = $ constant
Where, $P = $Pressure energy per unit volume
$\rho gh = $ Potential energy per unit volume
$\dfrac{1}{2}\rho {v^2} = $ Kinetic Energy per unit volume
In the above case the total energy at $A$is equal to total energy at $B$. So,
${P_A} + \rho aH + \rho gH = {P_B}$
Where, ${P_A} = $ Pressure energy per unit volume at $A$
$\rho aH = $ Kinetic Energy per unit volume at $A$
$\rho gH = $ Potential energy per unit volume at $A$
${P_B} = $ Total energy per unit volume at $B$
Now, given in the question that,
$\Rightarrow {P_A} = \dfrac{{{p_0}}}{2}$
$\Rightarrow {P_B} = {p_0}$
So, $\dfrac{{{p_0}}}{2} + \rho aH - \rho gH = {p_0}$
$\Rightarrow \rho H\left( {a - g} \right) = \dfrac{{{p_0}}}{2}$
$\Rightarrow a - g = \dfrac{{{p_0}}}{{2\rho H}}$
Therefore, $a = \dfrac{{{p_0}}}{{2\rho H}} + g$

Hence, option C is the correct answer.

Note: The atmosphere exerts the same pressure all over the earth’s surface. That pressure is known as atmospheric pressure. Its value is $1atm$. Bernoulli’s theorem is another form of proof for the Law of conservation of energy.