Question

Find the maximum extension in the spring.

A) $\dfrac{{{v_o}}}{4}\sqrt {\dfrac{m}{{5k}}} $
B) $\dfrac{{3{v_o}}}{4}\sqrt {\dfrac{m}{{5k}}} $
C) $\dfrac{{{v_o}}}{3}\sqrt {\dfrac{m}{{5k}}} $
D) $\dfrac{{{v_o}}}{8}\sqrt {\dfrac{m}{{5k}}} $

Answer 1

Hint: The maximum extension of the spring is defined as the elastic limit of the spring which can achieve due to the proportion of physical dimensions. A collision takes place when particles move towards each other and come near to interact and then exert a mutual influence.

Complete step by step solution:
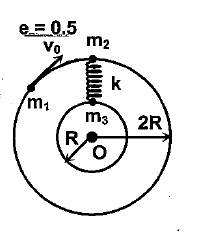
By conservation of linear momentum between $m_1$ and $m_2$ and also by using the coefficient of restitution,
The velocity of $m_2$ just after collision $ = \dfrac{{3{v_o}}}{4}$ $\left( {\because {V_f} = \dfrac{{{m_1}v}}{{{m_1} + {m_2}}}} \right)$
Similarly, after the collision, the maximum extension in the spring occurs when the angular velocity of $m_2$ and m3 about the point O becomes the same.
By conservation of angular momentum about O and by energy conservation,
Velocity of $m_2$ $ = r\omega = 2r\omega = \dfrac{3}{5}{v_o}$ $\left( {\because v = r\omega } \right)$
Similarly velocity of $m_3$ $ = r\omega = r\omega = \dfrac{3}{{10}}{v_o}$ $\left( {\because v = r\omega } \right)$
Thus maximum extension in the spring $ = \dfrac{{3{v_o}}}{4}\sqrt {\dfrac{m}{{5k}}} $ ${\because}$ k = Spring constant

Hence the correct option is B.

Note: 1) A coefficient of restitution equal to zero indicates a perfectly inelastic collision. Also, the coefficient of restitution indicates how elastic or inelastic the collision is.
2) The spring constant is defined as the ratio of the force affecting the spring to the displacement caused by it. It is denoted by k. When stretching a material, the limit of proportionality refers to the point beyond which Hooke’s law is no longer.
3) According to the principle of conservation of momentum, the total momentum of the system is unchanged in the collision process. Collisions are classified as elastic or inelastic based on whether mechanical energy or kinetic energy is conserved or not conserved.
4) The spring is said to be stiff if the spring constant is large and is said to be soft if the spring constant is small.