Work Energy and Power Class 11 Notes: CBSE Physics Chapter 5

1. WORK

In Physics, work refers to ‘mechanical work’. Work is said to be done by a force on a body when the body is actually displaced through some distance in the direction of the applied force.

However, when there is no displacement in the direction of the applied force, there is no work done, i.e., the work done is zero when the displacement of the body in the direction of the force is zero.

Consider a constant force ‘F’ acting on a body to produce a displacement ‘s’ in the body along the positive x-direction as shown in the following figure:

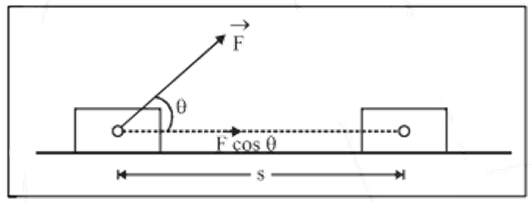
If $\theta $ is the angle which F makes with the positive x-direction of the displacement, then the component of F in the direction of displacement is given by $F\cos \theta $. Since the work done by the force is the product of the component of force in the direction of the displacement and the magnitude of the displacement, we can write:

$W=(F\cos \theta )s$

Now, when the displacement is in the direction of force applied, i.e., when $\theta ={{0}^{0}}$;

\[\Rightarrow W=\left( F\cos 0{}^\circ  \right)s=\vec{F}.\vec{s}\]

Clearly, work done by a force is the dot product of force and displacement.

In terms of rectangular components, $\vec{F}$ and $\vec{s}$ may be written as

\[\vec{F}=\hat{i}{{F}_{x}}+\hat{j}{{F}_{Y}}+\hat{k}{{F}_{Z}}\] and $\vec{s}=\hat{i}x+\hat{j}y+\hat{k}z$

$\Rightarrow W=\left( \hat{i}{{F}_{x}}+\hat{j}{{F}_{Y}}+\hat{k}{{F}_{Z}} \right).\left( \hat{i}x+\hat{j}y+\hat{k}z \right)$

$\Rightarrow W=x{{F}_{x}}+y{{F}_{y}}+z{{F}_{z}}$

Work is a scalar quantity, i.e., it has magnitude only and no direction. However, work done by a force can be positive, negative or zero.

2. DIMENSIONS AND UNITS OF WORK

As work $=$ force × distance;

$\Rightarrow W=({{M}^{1}}{{L}^{2}}{{T}^{-2}})\times L$

$\Rightarrow W=[{{M}^{1}}{{L}^{2}}{{T}^{-2}}]$

This is the dimensional formula of work.

The units of work are of two kinds: a) Absolute units and b) Gravitational units

a) Absolute Units

1. Joule: It is the absolute unit of work in the SI system of units. Work done is said to be one joule, when a force of one Newton actually moves a body through a distance of one meter in the direction of applied force.

$\Rightarrow 1joule=1newton\times 1metre\times \cos {{0}^{0}}=1N.m$

2. Erg: It is the absolute unit of work in the CGS system of units. Work done is said to be one erg, when a force of one dyne actually moves a body through a distance of one cm in the direction of applied force.

$\Rightarrow 1erg=1dyne\times 1cm\times \cos {{0}^{0}}=1dyne.cm$

b) Gravitational Units

These are also known as practical units of work.

1. Kilogram-meter (kg-m): It is the gravitational unit of work in the SI system of units. Work done is said to be one kg-m, when a force of 1kgf moves a body through a distance of 1m in the direction of the applied force.

$\Rightarrow 1kg-m=1kgf\times 1m\times \cos {{0}^{0}}=9.8N\times 1m=9.8joules$, i.e.,

$\Rightarrow 1kg-m=9.8J$

2. Gram-centimeter (g-cm): It is the gravitational unit of work in the CGS system of units. Work done is said to be one g-cm, when a force of 1gf

moves a body through a distance of 1cm in the direction of the applied force.

$\Rightarrow 1g-cm=1gf\times 1cm\times \cos {{0}^{0}}$

$\Rightarrow 1g-cm=980dyne\times 1cm\times 1$

$\Rightarrow 1g-m=980ergs$

3. NATURE OF WORK DONE

Although work done $\left( W=(F\cos \theta )s \right)$ is a scalar quantity, its value may be positive, negative, negative or even zero, as detailed below:

1. Positive Work is said to be done on a body when $\theta $ is acute ($<{{90}^{0}}$). Clearly, $\text{cos}\theta $ turns out to be positive and hence, the work done is positive.

For example, when a body falls freely under the action of gravity,$\theta ={{0}^{0}};\cos \theta =\cos {{0}^{0}}=+1$. Clearly, work done by gravity on a body falling freely is positive.

2. Negative Work is said to be done on a body when $\theta $ is obtuse ($>{{90}^{0}}$). Clearly, $\text{cos}\theta $  is negative and hence, the work done is negative.

For example, when a body is thrown up, its motion is opposed by gravity. The angle $\theta $ between gravitational force and the displacement is ${{180}^{0}}$. Since $\cos \theta =\cos {{180}^{0}}=-1$; work done by gravity on a body moving upwards is negative.

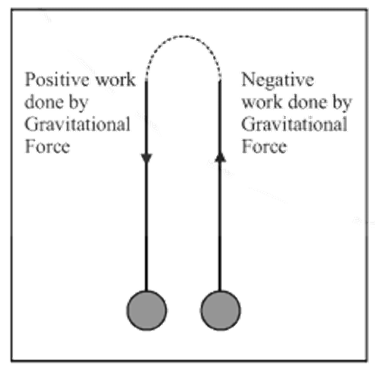
3. Zero Work is said to be done on a body when force is applied on it or the displacement caused or both of them are zero. Here, when angle $\theta $ between force and displacement is ${{90}^{0}}$; $\cos \theta =\cos {{90}^{0}}=0$ and hence, the work done is zero.

For example, when we push hard against a wall, the force we exert on the wall does not work because displacement is zero in this case. However, in this process, our muscles are contracting and relaxing alternately and internal energy is being used up. This is why we do get tired.

4. WORK DONE BY A VARIABLE FORCE

1. Graphical Method:

A constant force is rare. It is the variable force which is encountered more commonly. 

To evaluate the work done by a variable force, let us consider a force acting along a fixed direction, say the x–axis, but having a variable magnitude.

We have to compute work done in moving the body from A to B under the action of this variable force. 

To facilitate this, we assume that the entire displacement from A to B is made up of a large number of infinitesimal displacements.

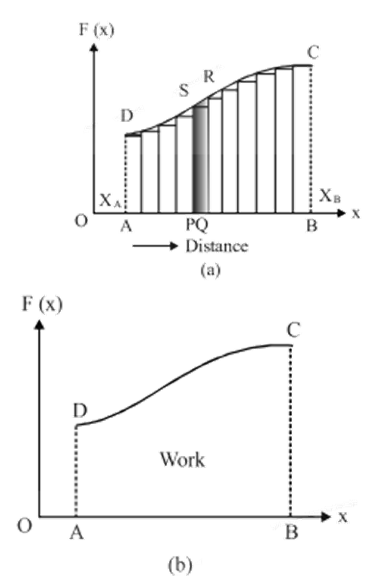
One such displacement is shown in the following figure from P to Q.

Since the displacement $PQ=dx$ is infinitesimally small, we consider that all along this displacement, force is constant in magnitude as well in the same direction.

Now, a small amount of work done in moving the body from P to Q is given by,

$dW=F\times dx=(PS)(PQ)=area\text{ }of\text{ }strip\text{ }PQRS$

Therefore, the total work done in moving the body from A to B is given by

$\Rightarrow W=\sum{dW}$

$\Rightarrow W=\sum{F\times dx}$

Here, when the displacement is allowed to approach zero, then the number of terms in the sum increases without a limit. And the sum approaches a definite value equal to the area under the curve CD.

Thus, we may rewrite that 

$\Rightarrow W=\underset{dx\to x}{\mathop{\lim }}\,\sum{F(dx)}$

Using integral calculus, we may write it as

$\Rightarrow W={}_{{{X}_{A}}}^{{{X}_{B}}}\int{A(dx)}$ 

Where,

${{x}_{A}}={{O}_{A}}$ and ${{x}_{B}}=OB$

$\Rightarrow W={}_{{{X}_{A}}}^{{{X}_{B}}}\int{area\text{ }of\text{ }strip\text{ }PQRS}$

Which is nothing but the total area under the curve between F and the x-axis from $x={{x}_{A\text{ }}}\text{ }to\text{  }x={{x}_{B}}$.

$\Rightarrow W=Area\text{ }of\text{ }ABCDA$

Clearly, the work done by a variable force is numerically equal to the area under the force curve and the displacement axis.

2. Mathematical Treatment (of work done by a variable force)

Suppose we have to evaluate the work done in moving a body from point A (${{S}_{A}}$) to point B (${{S}_{B}}$) under the action of a varying force as shown in the following figure. Here, ${{S}_{A}}$ and ${{S}_{B}}$ are the distance of the points A and B with respect to some reference point.

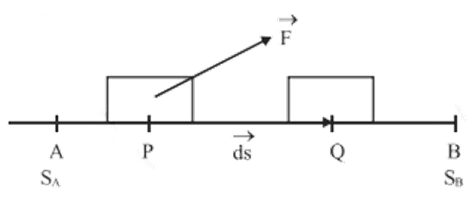
At any stage, let the body be at P, where the force on the body is $\vec{F}$. 

Under the action of this force, let the body undergo an infinitesimally small displacement $d\vec{s}$

During such a small displacement, if we assume that the force remains constant, then a small amount of work done in moving the body from P to Q is

given by,

$dW=\vec{F}.d\vec{s}$

Now, when the displacement is zero, the total work done in moving the body from A to B can be obtained by integrating the above expression between ${{S}_{A}}$and ${{S}_{B}}$ as follows:

\[\Rightarrow W={}_{{{S}_{A}}}^{{{S}_{B}}}\int{\vec{F}.d\vec{s}}\] 

5. CONSERVATIVE & NON­CONSERVATIVE FORCES

1. Conservative Force

A force is said to be conservative when the work done by or against the force in moving a body is dependent only on the initial and final positions of the body, and not on the nature of the path followed between the initial and the final positions.

This suggests that the work done by or against a conservative force in moving a body over any path between fixed initial and final positions would be the same.

For instance, gravitational force is a conservative force.

Properties of Conservative Forces:

• Work done by or against a conservative force in moving a body from one position to the other depends only on the initial position and final position of the body.

• Work done by or against a conservative force does not depend upon the nature of the path followed by the body in going from the initial position to the final position.

• Work done by or against a conservative force in moving a body through any round trip (i.e., closed path, where the final position coincides with the initial position of the body) is always zero.

2. Non-conservative Forces

A force is said to be non-conservative when the work done by or against the force in moving a body from one position to another, is dependent on the path followed between these two positions.

For instance, frictional forces are non-conservative forces.

6. POWER

The power of a person or machine refers to the time rate at which work is done by it.

Mathematically,

Power $=$ Rate of doing work $=$ $\frac{work\text{ }done}{time\text{ }taken}$

Thus, the power of a body measures how fast it can do the work.

$\Rightarrow P=\frac{dW}{dt}$

Now, it is known that $\text{dW=\vec{F}}\text{.d\vec{s}}$;

$\Rightarrow P=\frac{\vec{F}.d\vec{s}}{dt}$

But $\frac{d\vec{s}}{dt}=\vec{v}$, which is the instantaneous velocity.

$\Rightarrow P=\vec{F}.\vec{v}$

Dimensions of power is given by

$P=\frac{W}{t}=\frac{{{M}^{1}}{{L}^{2}}{{T}^{-}}}{{{T}^{1}}}=[{{M}^{1}}{{L}^{2}}{{T}^{-3}}]$

Units of power

The absolute unit of power in the SI system of units is watt, which is denoted by $W$.

$\Rightarrow P=\frac{W}{t}$

$\Rightarrow 1watt=\frac{1joule}{1\text{ }\sec }\Rightarrow 1W=1J{{s}^{-1}}$

Clearly, the power of a body is said to be one watt, when it can do one joule of work in one second. A bigger unit if power is horsepower (hp), given by

$1hp=746W$

7. ENERGY

The energy of a body refers to the capacity or ability of the body to do work.

8. KINETIC ENERGY

The kinetic energy of a body refers to the energy possessed by the body by virtue of its motion.

Here are some examples:

1. A bullet fired from a gun can pierce through a target on account of the kinetic energy of the bullet.

2. Windmills work on the kinetic energy of air. For instance, sailing ships use the kinetic energy of wind.

3. Water mills work on the kinetic energy of water. For instance, fast-flowing streams are utilized to grind corn.

4. A nail is driven into a wooden block on account of the kinetic energy of the hammer striking the nail.

The Formula for Kinetic Energy

Kinetic Energy of a body can be obtained either from

1. the amount of work done in stopping the moving body or from

2. the amount of work done in giving the present velocity to the body from the state of rest.

Let us first consider the second method:

Suppose that, 

m$=$ mass of a body at rest (i.e., u$=$0).

F$=$Force applied on the body

a$=$acceleration produced in the body in the direction of force applied.

v$=$velocity acquired by the body in moving through a distance ‘s’, as shown in the following diagram.

Now, consider the equation of motion: $v-u=2as$;

$\Rightarrow {{v}^{2}}-0=2as$

$\Rightarrow a=\frac{{{v}^{2}}}{2s}$

It is known that 

$F=ma$

$\Rightarrow F=m\left( \frac{{{v}^{2}}}{2s} \right)$

Clearly, work done on the body, (W $=$ Force × distance)

$\Rightarrow W=m\frac{{{v}^{2}}}{2s}\times s$

$\Rightarrow W=\frac{1}{2}m{{v}^{2}}$

This work done on the body is a measure of kinetic energy (K.E.) acquired by the body,

$\Rightarrow K.E\text{ }Of\text{ }the\text{ }body=W=\frac{1}{2}m{{v}^{2}}$

Alternative Method

The formula for kinetic energy of a body can also be obtained by the method of calculus as follows:

Let m$=$mass of a body, which is initially at rest (i.e., u$=$0)

$\vec{F}$$=$Force applied on the body,

$d\vec{s}$$=$ small displacement produced in the body in the direction of the force applied.

A small amount of work done by the force is given by,

$dW=\vec{F}.d\vec{s}=Fds\cos {{0}^{0}}=Fds$

If ‘a’ is the acceleration produced by the force, then from

$F=ma=m\frac{dv}{dt}$ and from 

$dW=\left( m\frac{dv}{dt} \right)ds=m\left( \frac{ds}{dt} \right)dv$;

$\Rightarrow dW=mvdv\text{     }\left( \because \frac{ds}{dt}=v \right)$

Thus, the total work done by the force in increasing the velocity of the body from zero to v is given by

$W=\int\limits_{0}^{v}{mvdv}=\frac{1}{2}m{{v}^{2}}$

Thus, the kinetic energy of a body is half the product of the mass of the body and the square of the velocity of the body.

9. RELATION BETWEEN KINETIC ENERGY AND LINEAR MOMENTUM

If m is the mass of a body and v is the velocity of the body;

Linear momentum of the body is given by \[p=mv\] and K.E. of the body is given by $KE=\frac{1}{2}m{{v}^{2}}=\frac{1}{2m}({{m}^{2}}v)$

$\Rightarrow KE=\frac{p}{2m}$

This is an important relation. It shows that a body cannot have kinetic energy without having linear momentum. The reverse is also true.

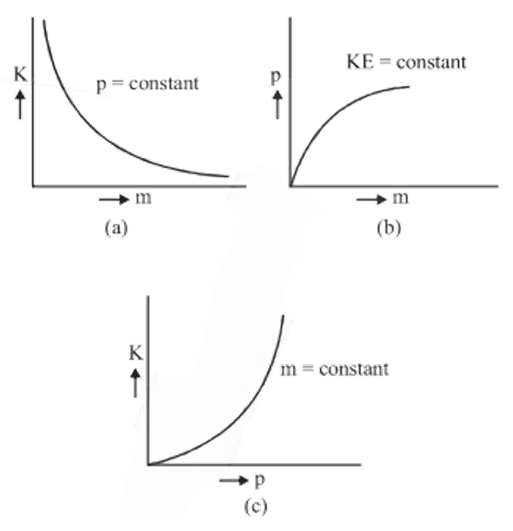
Further, if linear momentum (p) is constant, then,

$KE \propto \frac{1}{m}$

This is shown in Figure (a).

On the other hand, if kinetic energy (KE) is constant, then,

${{p}^{2}}\propto m\text{ }or\text{ }p\propto \sqrt{m}$

This is shown in Figure (b).

Also, if mass (m) is constant, the,

${{p}^{2}}\propto KE\text{ }or\text{ }p\propto \sqrt{KE}$

This is shown in Figure (c).

10. WORK ENERGY THEOREM OR WORK ENERGY PRINCIPLE

According to this principle, work done by the net force in displacing a body is the same as the change in kinetic energy of the body.

Thus, when a force does some work on a body, the kinetic energy of the body increases by the same amount. Conversely, when an opposing (retarding) force is applied to a body, its kinetic energy decreases. The decrease in kinetic energy of the body is equal to the work done by the body against the retarding force. Thus, according to the work-energy principle, work and kinetic energy are equivalent quantities.

Proof: To prove the work-energy theorem, we confine ourselves to motion in one dimension.

Suppose that m$=$mass of a body, u$=$initial velocity of the body, F$=$force applied on the body along its direction of motion, a$=$acceleration produced in the body, v$=$final velocity of the body after t second.

The small amount of work done by the applied force on the body is given by $dW=F(ds)$, when ds is the small distance moved by the body in the direction of the force applied.

Now, 

$F=ma=m\left( \frac{dv}{dt} \right)ds=m\left( \frac{ds}{dt} \right)dv=mvdv\left( \therefore \frac{\text{ds}}{\text{dt}}=v \right)$

Total work done by the applied force on the body in increasing its velocity from u to v is given by

\[W=\int\limits_{u}^{v}{mvdv}=m\left[ \frac{{{v}^{2}}}{2} \right]_{u}^{v}\]

$\Rightarrow W=\frac{1}{2}m(v-u)=\frac{1}{2}mv-\frac{1}{2}mu$

But $\frac{1}{2}m{{v}^{2}}={{K}_{f}}=final\text{ }KE\text{ }of\text{ }the\text{ }body\text{ }and\text{ }\frac{1}{2}m{{u}^{2}}={{K}_{i}}=initial\text{ }KE\text{ }of\text{ }the\text{ }body$

$\Rightarrow W={{K}_{f}}-{{K}_{i}}=increases\text{ }in\text{ }KE\text{ }of\text{ }body$

i.e., work done on the body is equal to the increase in KE of the body.

11. POTENTIAL ENERGY

The potential energy of a body refers to the energy possessed by the body by virtue of its position or configuration in some field.

Thus, potential energy is the energy that can be associated with the configuration (or arrangement) of a system of objects that exert forces on one another. Obviously, if the configuration of the system changes, then its potential energy changes.

Two important types of potential energy are:

1. Gravitational potential energy

2. Elastic potential energy.

11.1 Gravitational Potential Energy

The gravitational potential energy of a body refers to the energy possessed by the body by virtue of its position above the surface of the earth.

To calculate gravitational potential energy, suppose

m$=$mass of a body

g$=$acceleration due to gravity on the surface of the earth.

h$=$height through which the body is raised, as shown in the following figure.

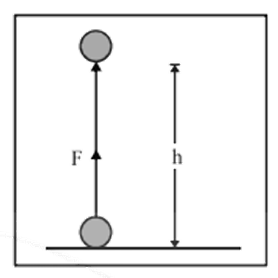
If we assume that height ‘h’ is not too large and the value of ‘g’ is practically constant over this height, then the force applied just to overcome gravitational attraction is given by,

$F=mg$

As the distance moved is in the direction of the force applied, work can be expressed as:

Work done$=$force × distance

$\Rightarrow W=F\times h=mgh$

Notice that we have taken the upward direction to be positive. Therefore, work done by applied force$=+mgh$. However, work done by gravitational force$=-mgh$.

This work gets stored as potential energy. The gravitational potential energy of a body, as a function of height (h) is denoted by V(h), and it is negative of work done by the gravitational force in raising the body to that height.$\Rightarrow Gravitational\text{ }PE=V(h)=mgh$

11.2 Potential Energy of a Spring

The potential energy of a spring refers to the energy associated with the state of compression or expansion of an elastic spring.

To compute it, consider an elastic spring OA of negligible mass. The end O of the spring is fixed to a rigid support and a body of mass ‘m’ is attached to the free end A. Let the spring be oriented along the x–axis and the body of mass ‘m’ lie on a perfectly frictionless horizontal table.

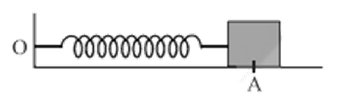
The position of the body A, when spring is unstretched, is chosen as the origin. Now, when the spring is compressed or elongated, it tends to recover to its original length, on account of elasticity. The force trying to bring the spring back to its original configuration is termed restoring force or spring force.

For a small stretch or compression, spring obeys Hooke's law, i.e., for a spring,

Restoring Force $\propto $ stretch or compression

$\Rightarrow -F\propto x\text{ }or\text{ }-F=kx$

where k is a constant of the spring called the spring constant.

It is established that for a spring, $k\propto \frac{1}{l}$. i.e., the smaller the length of the spring, the greater would be the force constant and vice-versa.

The negative sign in the equation indicates that the restoring force is always directed towards the equilibrium position.

Now, consider that the body be displaced further through an infinitesimally small distance dx, against the restoring force.

A small amount of work done in increasing the length of the spring by dx is given by,

$dW=-Fdx=kxdx$

Thus, the total work done in giving displacement x to the body can be obtained by integrating from $x=0$ to $x=x$, i.e.,

$W=\int\limits_{x=0}^{x=x}{kxdx}=\frac{1}{2}k{{x}^{2}}$

This work done is stored in the spring at the point B.

$\Rightarrow PE\text{ }at\text{ }B=W=\frac{1}{2}k{{x}^{2}}$

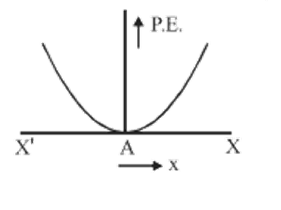
The variation of potential energy with distance x is as shown in the following figure.

12. MECHANICAL ENERGY AND ITS CONSERVATION

The mechanical energy (E) of a body refers to the sum of kinetic energy (K) and potential energy (V) of the body

i.e., $E=K+V$

Obviously, the mechanical energy of a body is a scalar quantity measured in joules.

We can show that the total mechanical energy of a system is conserved if the force doing work on the system is conservative.

This is known as the principle of conservation of total mechanical energy.

For simplicity, we assume the motion to be one-dimensional only. Suppose a body undergoes a small displacement ‘x’ under the action of a conservative force F. According to the work-energy theorem, change in kinetic energy is equal to the work done.

$\Rightarrow \Delta K=F(x)\Delta x$

Now, as the force is conservative, the potential energy function V(x) is defined as

\[-\Delta V=F(x)\Delta x\text{ }or\text{ }\Delta V=-F(x)\Delta x\]

Adding both the above expressions, we get,

$\Rightarrow \Delta K+\Delta V=0\text{ }or\text{ }\Delta (K+V)=0$,

which means that

$(K+V)=E=constant$

12.1 Illustration of the Law of Conservation of Mechanical Energy

To illustrate the law further, let us evaluate the kinetic energy, potential energy, and total energy of a body falling freely under gravity.

Let ‘m’ be the mass of the body held at A, at a height h above the ground, as shown in the following figure.

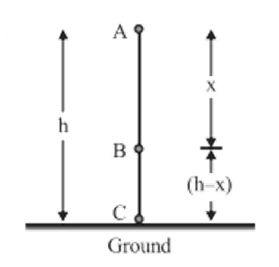
As the body is at rest at A, therefore,

At A;

KE of the body is zero.

PE of the body is equal to mg, where g is the acceleration due to gravity at A.

$\Rightarrow TE\text{ }of\text{ }the\text{ }body=KE+PE=0+mgh$

$\Rightarrow {{E}_{A}}=mgh$….(1)

Now, let the body be allowed to fall freely under gravity, when it strikes the ground at C with a velocity ‘v’.

From ${{v}^{2}}-{{u}^{2}}=2as$;

$\Rightarrow {{v}^{2}}-0=2(g)h$

$\Rightarrow {{v}^{2}}=2gh$….(2)

Therefore, at C;

KE of the body$=\frac{1}{2}m{{v}^{2}}=\frac{1}{2}m{{v}^{2}}=\frac{1}{2}m(2gh)=mgh$

PE of the body\[=mgh=mg\left( 0 \right)=0\]

The total energy of the body is given by,

$TE={{E}_{C}}=mgh+0=mgh$.... (3)

Now, in free fall, let the body cross any point B with a velocity ${{v}_{1}}$, where AB is equal to ‘x’. Thus, from ${{v}^{2}}-{{u}^{2}}=2as$;

$\Rightarrow v_{1}^{2}-0=2(g)x$…. (4)

$\Rightarrow v_{1}^{2}=2gx$

Clearly, at B;

KE of the body$=\frac{1}{2}mv_{1}^{2}=\frac{1}{2}m(2gx)=mgx$

Height of the body at B above the ground\[=CB=\left( hx \right)\]

PE of the body at B\[=mg\left( hx \right)\]

The total energy of the body at B\[=KE+PE\]

$\Rightarrow {{E}_{B}}=mgx+mg(h-x)=mgx+mgh-mgx$

$\Rightarrow {{E}_{B}}=mgh$.... (5)

Clearly, from (1), (3), and (5); we find that

${{E}_{A}}={{E}_{C}}={{E}_{B}}=mgh$

13. DIFFERENT FORMS OF ENERGY

We have learnt some details of potential energy and kinetic energy. It should be understood that these are not the only two forms of energy. Energy may manifest itself in several other forms. Some of the examples are:

1. Heat Energy

It is the energy possessed by a body by virtue of the random motion of the molecules of the body.

Heat is also associated with the force of friction. When a block of mass ‘m’ sliding on a rough horizontal surface with speed ‘v’, stops over a distance ‘x’, work done by the force of kinetic friction ‘f’ over a distance ‘x’ is given by $-f(x)$. By the work energy theorem, $\frac{1}{2}m{{v}^{2}}=f(x)$ .We often say that the kinetic energy of the block is lost due to frictional force. However, when we examine the block and the horizontal surface carefully, we detect a slight increase in their temperatures. Thus, work done by friction is not lost, but is transferred as heat energy of the system.

2. Internal Energy

It is the total energy possessed by the body by virtue of the particular configuration of its molecules and also their random motion. Thus, the internal energy of a body is the sum of the potential energy and kinetic energy of the molecules of the body.

3. Electrical Energy

The flow of electric current causes bulbs to glow, fans to rotate and bells to ring. A definite amount of work has to be done in moving the free charge carriers in a particular direction through all the electrical appliances.

4. Chemical Energy

Chemical energy arises from the fact that the molecules participating in the chemical reaction have different binding energies. A chemical reaction is basically a rearrangement of atoms. For example, coal consists of carbon and a kilogram of it. When burnt, it releases $3\times {{10}^{7}}J$ of energy.

5. Nuclear Energy

It is the energy obtainable from an atomic nucleus. Two distinct modes of obtaining nuclear energy are nuclear fission and nuclear fusion.

Nuclear fission involves the splitting of a heavy nucleus into two or more lighter nuclei, whereas nuclear fusion involves the fusing of two or more lighter nuclei to form a heavy nucleus.

14. MASS ENERGY EQUIVALENCE

Einstein made an incredible discovery that energy can be transformed into mass and mass can be transformed into energy. To put it precisely, one energy can be obtained at the cost of the other energy.

The mass-energy equivalence relation as put forth by Einstein is

$E=m{{c}^{2}}$

Where,

m is the mass that disappears; 

E is the energy that appears;

C is the velocity of light in a vacuum.

Mass and energy are not conserved separately, but are conserved as a single entity called ‘mass-energy’.

15. THE PRINCIPLE OF CONSERVATION OF ENERGY

If we account for all forms of energy, the total energy of an isolated system does not change.

The principle of conservation of energy cannot be proved as such. However, no violation of this principle has ever been observed.

16. WORK DONE BY A VARIABLE FORCE

When the force is an arbitrary function of position, we require the techniques of calculus to determine the work done by it. The figure shows F(x) as some function of the position x. To calculate work done by F from A to B, we find the area under the graph from ${{X}_{A}}\text{ }to\text{ }{{X}_{B}}$.

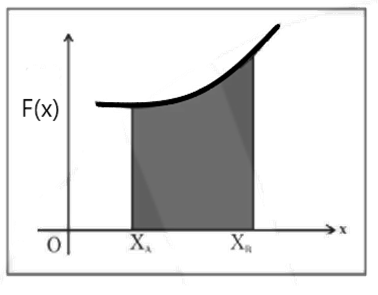
Thus, the work done by a force F(x) from an initial point A to the final point B is given by,

${{W}_{A\to B}}=\int\limits_{{{X}_{A}}}^{{{X}_{B}}}{{{F}_{X}}dx}$

17. CONSERVATIVE & NON­CONSERVATIVE FORCES

17.1 Conservative Forces

A force is conservative if the net work done against the force in moving a mass between two points depends only on the location of two points and not on the path followed.

17.2 Non-Conservative Forces

Those forces which do not satisfy the above-mentioned criteria are termed non-conservative forces. Friction and viscous forces are the most common examples of non-conservative forces.

17.3 Conservative Forces and Potential Energy

For every conservative force, there is a corresponding potential energy function. In each case, the potential energy expression is dependent only on position. For every conservative force ${{F}_{X}}$, that depends only on the position ‘x’, there is an associated potential energy function U(x). When conservative force does positive work, the potential energy of the system decreases. Work done by a conservative force is given as:

$F(x)\Delta x=-\Delta U$

$\Rightarrow F(x)=\frac{-\Delta U}{\Delta x}$

which, in the limit, becomes, 

$\Rightarrow F(x)=-\frac{dU}{dx}$

Integrating both sides for a displacement from\[x=a\text{ }to\text{ }x=b\], we have,

\[\Rightarrow {{U}_{b}}-{{U}_{a}}=-\int\limits_{b}^{a}{F(x)dx}\]

18. DYNAMICS OF CIRCULAR MOTION

18.1 Force on the Particle

In a uniform circular motion, acceleration is of magnitude $\frac{{{v}^{2}}}{r}$ and is directed towards the center. Thus, a force of magnitude $\frac{m{{v}^{2}}}{r}$ and directed towards the centre is needed to keep a particle in a circular motion. 

This force (acting toward the centre) is called the centripetal force. Centripetal force is not an extra force on a body. Whatever force is responsible for circular motion becomes the centripetal force.

Examples 

When a satellite revolves around the earth, the gravitational attraction of the earth becomes the centripetal force for the circular motion of that satellite; 

When an electron revolves around the nucleus in an atom, the electrostatic attraction of the nucleus becomes the centripetal force for the electron’s circular motion. 

In the case of a conical pendulum, \[Tsin\theta \](component of tension) becomes the centripetal force.

18.2 Main steps for analyzing forces

Consider an axis along the radius of the circle (i.e., in the direction of acceleration) and another axis perpendicular to the radius. Resolve all the forces into components.

Net force along the perpendicular axis is equal to zero.

Net force along radial axis (towards center)$=\frac{m{{v}^{2}}}{r}=m{{\omega }^{2}}r$.

18.3 Main Steps for Analyzing Forces in Non–Uniform Circular Motion

Once we resolve all the forces along tangential and radial axes;

Net tangential force $={{F}_{t}}=m{{a}_{t}}$

Net radial force = $={{F}_{r}}=m{{a}_{r}}=\frac{m{{v}^{2}}}{r}$

Example of non-uniform circular motion 

The motion of particles in a vertical circle. If a particle is revolved in a vertical circle with the help of a string, the forces are: tension (T) towards center and weight (mg). 

In the case of a particle moving along the outside surface of a circular track (or sphere), the forces are: normal reaction (N) away from the center and weight (mg).

18.4 Conical Pendulum

A small block of mass ‘m’ is rotated in a horizontal circle with the help of a string of length ‘l’ connected to ‘m’. The other end of the string is fixed to a point O vertically above the center of the circle so that the string is always inclined with the vertically at an angle. Such an arrangement is referred to as a conical pendulum as shown in the following diagram.

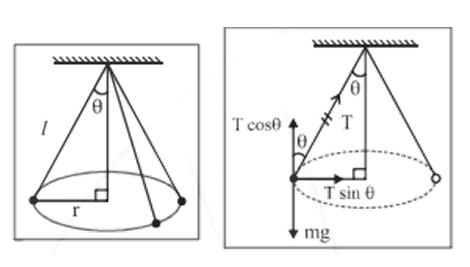
With respect to the force diagram of the block;

Along the vertical:

$T\cos \theta =mg$…(1)

Net force towards center,

\[Tsin~\theta =ma\]

$\Rightarrow \text{Tsin}\theta \text{=m}{{\omega }^{2}}r$…(2)

From (1) and (2), we have,

\[{{\omega }^{2}}=\frac{g\tan \theta }{r}=\frac{g\tan \theta }{l\sin \theta }=\frac{g}{l\cos \theta }\]

$\Rightarrow Time\text{ }period=T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{l\cos \theta }{g}}$

Note:

• If ‘h’ is the height of point O above the center of the circle, then time period is equal to $2\pi \sqrt{\frac{h}{g}}$.

• For a conical pendulum, 

${{\omega }^{2}}l\cos \theta =g$

$\Rightarrow \omega >\sqrt{\frac{g}{l}}$ (Because \[cos~\theta <l\])

18.5 Motion in a Vertical Circle

For a mass ‘m’ tied to a string of length ‘l’ and rotated in a vertical circle with center at the other end of the string, let is determine:

(a) the minimum velocity of the mass at the top of the circle so that it is able to complete the circle.

(b) the minimum velocity at the bottom of the circle.

At all positions, there are two forces acting on the mass: its own weight and the tension in the string.

Let the radius of the circle be equal to one unit.

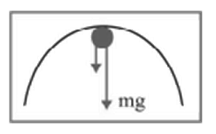
(a) At the Top 

Let ${{v}_{t}}=$velocity at the top;

Net force towards center$=\frac{mv_{t}^{2}}{l}$

$T+mg=\frac{mv_{t}^{2}}{l}\Rightarrow T=\frac{mv_{t}^{2}}{l}-mg$

For the movement in the circle, the string must remain tight i.e., the tension should be positive at all positions.

As the tension is minimum at the top ${{\text{T}}_{top}}\ge 0$;

$\Rightarrow \frac{mv_{t}^{2}}{l}-mg\ge 0\Rightarrow {{v}_{t}}\ge \sqrt{{{l}_{g}}}$

$\Rightarrow $ minimum or critical velocity at the top = $=\sqrt{{{l}_{g}}}$

(b) At the Bottom

Let ${{v}_{b}}$ be the velocity at the bottom. As the particle goes up, its kinetic energy decreases and gravitational potential energy increases.

$\Rightarrow $loss in KE is equal to gain in GPE

$\Rightarrow \frac{1}{2}mv_{b}^{2}-\frac{1}{2}mv_{1}^{2}=mg(2l)$

$\Rightarrow v_{b}^{2}=v_{t}^{2}+4gl$

$\Rightarrow {{({{v}_{b}})}_{\min }}=\sqrt{{{(v_{t}^{2})}_{\min }}+4gl}=\sqrt{5gl}$

Note:

When a particle moves in a vertical circle, its speed reduces as it goes up and its speed rises as it comes down. Clearly, it is an example of non-uniform circular motion.

Here in Vedantu, we believe in the quality of education. Many students rely on the Vedantu program. We do not break their trust. Many students were successful in past years and we plan to do something different to make it more comfortable for the aspirants.

Students presently studying in Class 11 are welcome to join us. This program is completely based on the CBSE board syllabus. This program is helpful for those who want to get the best marks.

CBSE Class 11 Physics Notes Chapter 5 Work, Power and Energy

In this context, we are going to discuss the list of content on what is work, power and energy. When we talk about Physics, the chapter on work, power, and energy is one of the most important chapters which involves concepts of mechanics.

The utmost collective illustrations that aid a concept of work, power and energy are a car in motion, bracing heavy objects, walking upstairs, an aeroplane flying and so on.

Some concepts regarding Chapter Work, Power, and Energy are precisely described in physics. So, these concepts can help you to do some measurements. Also, these perceptions can be utilized to describe and calculate the motion and its behaviour among multiple figures.

Chapter 5 Physics Class 11 Notes

• What do you mean by Work?

Work can be defined as the amount of energy that transfers when a body is moved by an outside (external) force propagated in the displacement’s direction.

• What do you mean by Power?

The definition of power can be explained as the rate at which the work is accomplished. Mathematically, Power = Work/time

• What do you mean by Energy?

The definition of energy can be explained as the capability of doing work.

Energy has many forms. The most popular forms of energy are kinetic, thermal, potential, electrical, chemical, nuclear, etc.

The SI unit of work and energy is the same.

There is a list of physics of class 11 chapter 5 work, energy, and power.

Here are some Frequently asked questions under Class 11 Chapter 5 Physics Notes.

Q1. The aircraft casing burns up by friction. Find the energy obtained required for the burning of the casing.

Ans: The mass of the rocket reduces at the time of the burning of the casing due to the friction.

No reaction is beyond the law of conservation of energy. 

So, ETotal = Potential energy + Kinetic energy = mgh + ½ mv2

It is noticed that a drop in total energy happens due to the reduction in the mass of the aircraft. That is the reason for which energy is required for the burning of the casing which is obtained from the rocket.

Q2. If a ball of mass 5 kg is placed on a higher ground of 3 meters, find the potential energy stored in that body.

Ans: Given, m = 5 kg

h = 3 m

We know that g = 9.81 m/s-2

So, Potential energy = m * g * h = 5 * 3 * 9.81 = 147.15 J

Short Answer Type Questions

1.  A spring is kept compressed by pressing its ends together lightly. It is then placed in strong acid and released. What happens to its stored potential energy?

2. Why are the clock pendulums made of invar, a material of low value of the coefficient of linear expansion?

3. How would a thermometer be different if glass expanded more with increasing temperature than mercury?

Long Answer Type Questions

1. An object of mass 0.4kg moving with a velocity of 4m/s collides with another object of mass 0.6kg moving in the same direction with a velocity of 2m/s. If the collision is perfectly inelastic, what is the loss of K.E. due to impact?

2. A ball is dropped on the floor from a height of 2cm. After the collision, it rises up to a height of 1.5m. Assuming that 40% of mechanical energy lost goes to thermal energy into the ball. Calculate the rise in temperature of the ball in the collision. The specific heat capacity of the ball is 800J/k. Take g = 10m/s².

3. If the volume of a block of metal changes by 0.12% when it is heated to 200C. What is the coefficient of linear expansion of the metal?

Practice Questions

1. If one Mole of a monatomic gas is mixed with 3 moles of a diatomic gas. What is the molecular-specific heat of the mixture at constant volume?

2. A stone of mass 5 kg falls from the top of a cliff 30 m high and buries itself one metre deep into the sand. Find the average resistance offered and the time taken to penetrate into the sand.

3. A pump on the ground floor of a building can pump up water to fill a tank of volume 30m³ in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?

Class 11 Physics Chapter 5 - Work, Energy and Power Formulas

1. Work Done (W):
$W = \vec{F} \cdot \vec{s} = F s \cos \theta$
Where F is the force, sss is the displacement, and $\theta$ is the angle between the force and displacement vectors.

2. Kinetic Energy (KE):
$KE = \frac{1}{2} m v^2$

Where mmm is the mass and v is the velocity of the object.

3. Potential Energy (PE):
PE = mgh
Where m is the mass, g is the acceleration due to gravity, and h is the height above the reference point.

4. Work-Energy Theorem:
$W = \Delta KE = KE_{\text{final}} - KE_{\text{initial}}$
This theorem states that the work done on an object is equal to the change in its kinetic energy.

5. Power (P):
$P = \frac{W}{t} = \vec{F} \cdot \vec{v}$

Where PPP is power, WWW is work, ttt is time, and vvv is velocity.

6. Gravitational Potential Energy (U):

U=mgh
Where h is the height, m is the mass, and g is the gravitational acceleration.

7. Conservation of Mechanical Energy:
$KE + PE = \text{constant}$

For a system with only conservative forces, the total mechanical energy (sum of kinetic and potential energy) remains constant.

8. Elastic Potential Energy (for a spring):
$U = \frac{1}{2} k x^2$
Where k is the spring constant and xxx is the displacement from equilibrium.

Section – A (1 Mark Questions)

1. What is the unit of Power?

Ans. Watt (W)

2. Name the factors on which work is done depends.

Ans. Force, displacement and angle between force and displacement.

3. Work done by external forces is always equal to the gain in kinetic energy. Is it always true ? 

Ans. Yes. This is the universal work-energy theorem.

4. If energy is neither created nor destroyed, then from where do we get energy?

Ans. By transforming energy from one form to another.

5. A force $F=5\hat{i}+6\hat{j}-4\hat{k}$ acting on a body, produce a displacement $s=6\hat{i}+5\hat{k}$ Work done by the force.

Ans. $W=F\cdot s=\left ( 5\hat{j}+6\hat{j}-4\hat{k} \right )\left ( 6\hat{i}+5\hat{k} \right )$

=30-20=10 units

Section – B (2 Marks Questions)

6. List two conditions which need to be satisfied for the work to be done on an object?

Ans. 

(i) Force should be applied on the body.

(ii) Body should move in the direction of force.

7. An archer stretches a bow to release an arrow to hit the target at a distance of 10 m. Explain who does the work, in which form is the energy possessed by the bow and the arrow.

Ans. The archer does the work in pulling the bow string taut. The muscular energy of the archer arm a → potential energy of the taut string → kinetic energy of the arrow.

8. A porter lifts a luggage of 15 kg from the ground and puts it on his head 1.5 m above the ground. Calculate the work done by him on the luggage.

Ans. Work done = Force × displacement

= mg × h

= 15 × 10 × 1.5

= 225 J.

9. A man of mass 60 kg runs up a flight of 30 steps in 40 s. If each step is 20 cm high, calculate his power. (take g = 10 m/s2)

Ans. Total height reached by $man=30\times \dfrac{20}{100}m=6m$

Power = work done/time = mgh / time 

$=\dfrac{60\times 10\times 6}{40}=90V$

10. An electric bulb of 100 W works for 4 hours a day. Calculate the units of energy consumed in 15 days.

Ans. Energy consumed = Power × Time

= 100 × 4 × 15

= 6000 Wh

= 6 KWh = 6 units

Important Topics of Class 11 Physics Chapter 5 Work Energy and Power

• The work-energy theorem

• Work

• Kinetic Energy

• Potential Energy

• Work done by a variable force

• The conservation of mechanical energy

• Power

Importance of Physics Class 11 Physics Chapter 5 Work Energy and PowerRevision Notes 

• Class 11 Work Energy And Power Notes highlight differences between positive and negative work, allowing students to understand various scenarios of work done in physics.

• They break down complex topics such as power and energy into manageable sections, which enhances learning efficiency.

• Detailed illustrations and examples make the concepts more visual and engaging, which helps retain information better.

• They help students master the use of important formulas by providing practical applications and examples.

• Class 11 Work Energy And Power Notes are aligned with the CBSE syllabus, ensuring that students study relevant material for their exams.

Tips for Learning the Class 11 Chapter 5 Physics Work Energy and Power

• Focus on understanding the core concepts of work, energy, and power. Know the difference between kinetic and potential energy and how they relate to the work-energy theorem.

• Ensure you're comfortable with key formulas like W=F×d×cosθ for work and  for kinetic energy KE= $\dfrac{1}{2} \times MV^2$. Practice applying these to different problems.

• Draw free-body diagrams and graphs to visualise the forces, directions, and work done in various situations.

• Regularly practice solving numerical problems to become familiar with different types of work, energy, and power-related questions.

• Relate the concepts to everyday situations, such as how energy is used in mechanical systems or the power required to run machines.

• Divide complex questions into smaller steps to make solutions more manageable and easier to understand.

• Create Work Energy And Power Class 11 Short Notes by your own language for better understanding and preparations.

• Revise the laws of conservation of energy and mechanical work regularly to reinforce your understanding.

Conclusion

The CBSE Class 11 Notes on Work, Energy, and Power offer a comprehensive and concise resource for understanding the fundamental concepts that govern the dynamics of energy in the physical world. The chapter explores the concept of work done, the various forms of energy, and their interconversion, providing students with a solid foundation in this essential aspect of physics. With these free PDF notes at their disposal, students can reinforce their understanding, revise key points, and practice important equations. By mastering the principles of work, energy, and power, students can confidently approach complex physics problems and delve deeper into the fascinating world of energy transformations and their practical applications.