Question

Consider the following statements: For non-empty sets. A, B and C
1. $$A-\left(B-C\right)=\left(A-B\right)\cup C$$
2. $$A-(B\cup C)=\left(A-B\right)-C$$

Which of the statements given above is/are correct?
A) 1 Only
B) 2 Only
C) Both 1 and 2
D) Neither 1 nor 2

Answer 1

Hint: In this question, we have to find which of the given condition is correct. In order to find this concept of Venn diagram is used. Apply concept of Venn diagram on given options to get the correct option.

Formula used: In this question we are going to use the Venn diagram. This diagram give the relation between various set and their subset.

Complete step by step solution: Draw a Venn-diagram taking three intersecting sets A, B and C under a universal set U. After intersection eight regions will be developed.

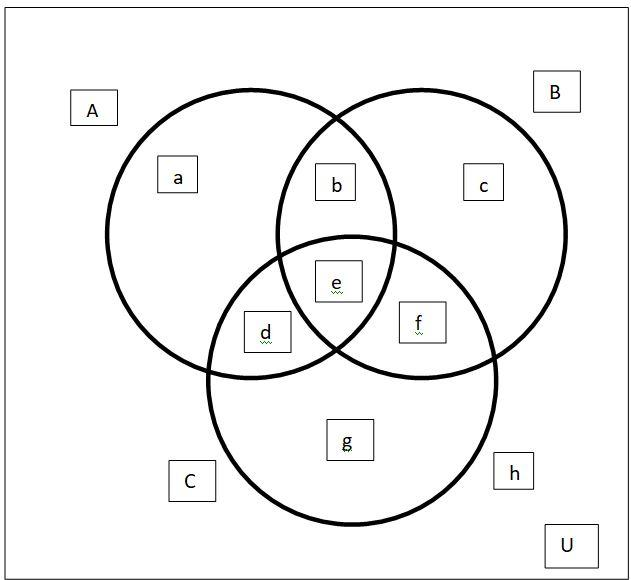
Now we have $$A-\left(B-C\right)=\left(A-B\right)\cup C$$, $$A-(B\cup C)=\left(A-B\right)-C$$

First statement: $$A-\left(B-C\right)=\left(A-B\right)\cup C$$
LHS contain only a while RHS contain a,d,c
Therefore First statement is wrong

Second Statement: $$A-(B\cup C)=\left(A-B\right)-C$$
LHS contain only a and RHS also contain a
Therefore statement second is correct.

Thus, Option (B) is correct.

Note: Here we must remember the algebra used in Venn diagram.
Some important properties of Sets are given below:
A. Idempotent Law is given as
(i) Union of two same sets $$A\cup A=A$$
(ii) Intersection of two same sets $$A\cap A=A$$

B. Associative Law is given as
(i) $$\left(A\cup B\right)\cup C=A\cup \left(B\cup C\right)$$
(ii) $$\left(A\cap B\right)\cap C=A\cap \left(B\cap C\right)$$

C. Commutative Law is given as
(i) $$A\cup B=B\cup A$$
(ii) $$A\cap B=B\cap A$$

D. Distributive law is given as
(i) $$A\cup \left(B\cap C\right)=\left(A\cup B\right)\cap \left(A\cup C\right)$$
(ii) $$A\cap \left(B\cup C\right)=\left(A\cap B\right)\cup \left(A\cap C\right)$$
Where A, B, C are set or subset of any universal set

E. De Morgan’s law is given as
(i) $${\left(A\cup B\right)}^c=A^c\cap B^c$$
(ii) $${\left(A\cap B\right)}^c=A^c\cup B^c$$
Where, $$A^c,B^c$$ is complement of set A and B respectively