Question

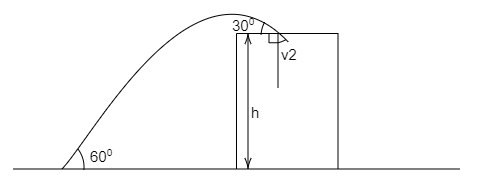
A stone projected at an angle of ${60^ \circ }$ from the ground level strikes a building of height $h$ at an angle of ${30^ \circ }$. Then the speed of projection of the stone is:



(A) $\sqrt {2gh} $
(B) $\sqrt {6gh} $
(C) $\sqrt {3gh} $
(D) $\sqrt {gh} $

Answer 1

Hint: The speed of the projection is determined by using the equation of the projectile motion, and here one condition is used, that is the final velocity in $x$ direction is equal to the initial velocity of the $x$ direction. Because there is no acceleration in the $x$ direction in the final velocity. By using this assumption, the speed can be determined.

Useful formula
The equation of the projectile motion is given by,
${v^2} - {u^2} = 2gh$
Where, $v$ is the final velocity of the stone, $u$ is the initial velocity of the stone, $g$ is the acceleration due to gravity and $h$ is the height of the building where the stone strikes.

Complete step by step solution
Given that,
The initial angle of projection is, $\theta = {60^ \circ }$,
The height of the building is, $h$,
The stone strikes the top of the building at an angle of, $\beta = {30^ \circ }$.
Now,
The initial angle of projection is, $\theta = {60^ \circ }$,
The initial velocity in $x$ direction is, ${u_x} = u\cos {60^ \circ }$,
The initial velocity in $y$ direction is, ${u_y} = u\sin {60^ \circ }$
Assume that the final velocity in $x$ direction is equal to the initial velocity in $x$ direction, because there is no acceleration in the $x$ direction, then
${v_x} = {u_x}$,
Now,
$\tan \beta = \dfrac{{{v_y}}}{{{v_x}}}$
Now the above equation is written as,
$\tan \beta = \dfrac{{{v_y}}}{{{u_x}}}$
By substituting the angle and the initial velocity in the $x$ direction in the above equation, then
$\tan {30^ \circ } = \dfrac{{{v_y}}}{{u\cos {{60}^ \circ }}}$
From the trigonometry, the value of $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$ and $\cos {60^ \circ } = \dfrac{1}{2}$, then the above equation is written as,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{{v_y}}}{{u \times \dfrac{1}{2}}}$
By rearranging the terms in the above equation, then the above equation is written as,
${v_y} = \dfrac{u}{{2\sqrt 3 }}$
Now, the projectile equation of motion is given by,
${v_y}^2 - {u_y}^2 = 2gh\,.......................\left( 1 \right)$
By substituting the value of $v$ and $u$ in the direction of $y$, then
${\left( {\dfrac{u}{{2\sqrt 3 }}} \right)^2} - {\left( {u\sin {{60}^ \circ }} \right)^2} = - 2gh$
The negative sign indicates that the acceleration acts downwards.
By substituting the sine value, then
${\left( {\dfrac{u}{{2\sqrt 3 }}} \right)^2} - {\left( {u \times \dfrac{{\sqrt 3 }}{2}} \right)^2} = - 2gh$
By suing the square in the above equation, then
$\dfrac{{{u^2}}}{{4 \times 3}} - \dfrac{{3{u^2}}}{4} = - 2gh$
By multiplying the terms in the above equation, then
$\dfrac{{{u^2}}}{{12}} - \dfrac{{3{u^2}}}{4} = - 2gh$
By cross multiplying the terms, then
$\dfrac{{4{u^2} - 36{u^2}}}{{48}} = - 2gh$
By subtracting the terms, then
$\dfrac{{ - 32{u^2}}}{{48}} = - 2gh$
By cancelling the terms and cancelling the negative sign on both sides, then
$\dfrac{{8{u^2}}}{{12}} = 2gh$
By rearranging the terms, then the above equation is written as,
${u^2} = \dfrac{{2gh \times 12}}{8}$
By multiplying the terms in the above equation, then
${u^2} = \dfrac{{24gh}}{8}$
By dividing the terms in the above equation, then
${u^2} = 3gh$
By taking square root on both sides, then
$u = \sqrt {3gh} $

Hence, the option (C) is the correct answer.

Note: The negative sign is included after equation (1) is because of the acceleration due to gravity which pulls the stone downwards when the stone is moving in upward direction. So, the acceleration due to gravity acts in the opposite direction to the direction of the stone. So, the negative sign is included.