Question

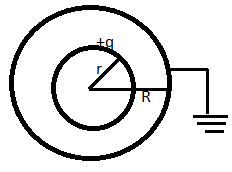
A spherical capacitor has an inner sphere of radius $12cm$ and an outer sphere of radius $13cm$. The outer sphere is earthed and the inner sphere is given a charge of $2.5\mu C$. The space between the concentric spheres is filled with liquid of dielectric constant $32.$
A) Determine the capacitance of the capacitor.
B) What is the potential of the inner sphere?
C) Compare the capacitance of the capacitor with that of an isolated sphere of radius $12cm$. Explain why the latter is much smaller.

Answer 1

Hint: The capacitance of a system only depends on the geometry and the medium between the two plates/surfaces. An isolated sphere is nothing but a sphere with one spherical surface(outer one) is taken to infinity.

Formula Used:
Capacitance for spherical capacitor
$C=4\pi {{\varepsilon }_{0}}K\dfrac{rR}{R-r}$

Complete step by step answer:
 A spherical capacitor consists of a solid or hollow spherical conductor of radius $r$, surrounded by another hollow concentric spherical of radius $R$.
Potential difference between two conductors
$V=\dfrac{q}{4\pi {{\varepsilon }_{0}}K}\dfrac{\left( R-r \right)}{Rr}$ ………….(i)

Capacitance of spherical conductor
$C=\dfrac{q}{V}$
$C=\dfrac{q}{\dfrac{q}{4\pi {{\varepsilon }_{0}}K}\dfrac{\left( R-r \right)}{Rr}}=4\pi {{\varepsilon }_{0}}K\dfrac{Rr}{\left( R-r \right)}$
(a) $C=4\pi {{\varepsilon }_{0}}K\dfrac{\left( R-r \right)}{Rr}$ ………………….(ii)
Where
$R=$ Outer sphere radius
$r=$ Inner sphere radius
$K=$ Dielectric constant
$K=32$
$R=13cm=13\times {{10}^{-2}}m$
$r=12cm=12\times {{10}^{-2}}m$
$C=\dfrac{1}{9\times {{10}^{9}}}\dfrac{32\times 13\times {{10}^{-2}}\times 12\times {{10}^{-2}}}{\left( 13-12 \right)\times {{10}^{-2}}}$
$C=554.66\times {{10}^{-11}}$
$C=5.5\times {{10}^{-9}}F$
(b)
$\begin{align}
  & V=\dfrac{q}{C} \\
 & \Rightarrow V=\dfrac{2.5\times {{10}^{-6}}}{5.5\times {{10}^{-9}}} \\
 & \Rightarrow V=4.5\times {{10}^{2}} \\
 & \Rightarrow V=450V \\
\end{align}$
(c)For isolated sphere
$R\to \infty $
$\begin{align}
& C=4\pi {{\varepsilon }_{0}}\dfrac{1}{\left( \dfrac{1}{r}-\dfrac{1}{R} \right)} \\
& C'=4\pi {{\varepsilon }_{0}}r \\
\end{align}$
$\begin{align}
& \Rightarrow C'=\dfrac{1}{9\times {{10}^{9}}}\times 12\times {{10}^{-2}} \\
& \Rightarrow C'=1.33\times {{10}^{-11}}F \\
\end{align}$

The capacity of an isolated sphere is much smaller, because in a capacitor, the outer sphere is earthed, potential difference decreases and capacitance increases.

Note: When we find out the capacitance for hollow spherical capacitors sometimes we use the formula of a single sphere capacitor directly. This is the wrong method first we find out the potential difference between the spheres and then capacitance.