Question

A ring moves in a horizontal circle of radius $r$ with a velocity $\omega $ in free space the tension is:

(A) $2mr{\omega ^2}$
(B) $mr{\omega ^2}$
(C) $\dfrac{{mr{\omega ^2}}}{2}$
(D) $\dfrac{{mr{\omega ^2}}}{{2\pi }}$

Answer 1

Hint: We know that in order to move in a circular path we require a centripetal force. Centripetal force is the component of force acting on an object in curvilinear motion which is directed toward the axis of rotation or center of curvature. Now in the above case one of the components of tension is responsible for the centripetal force.

Complete step by step solution:
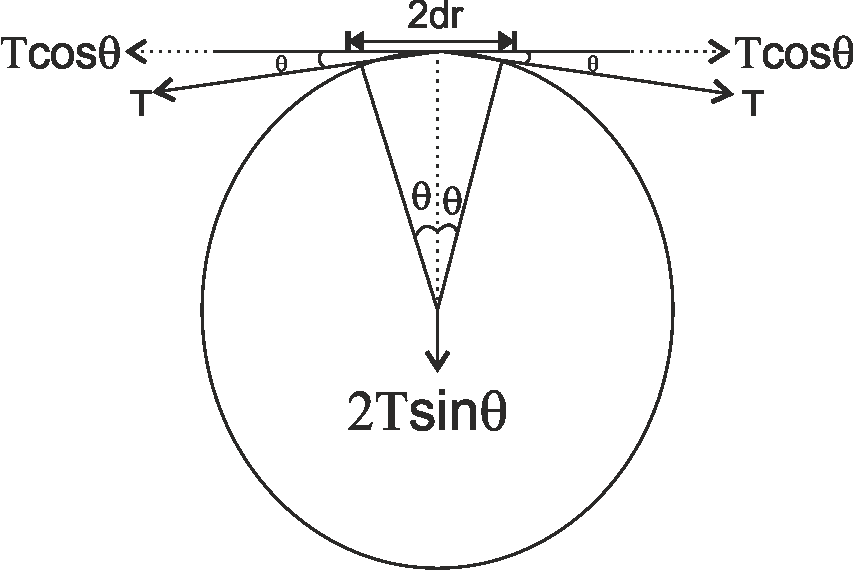
Let us consider a small element of length $2dr$ making angle $2\theta $ at the center and having mass $dm$
Now the centripetal force is given by
$F = mr{\omega ^2}$
Then the centripetal force due to that mass element is,
$F = (dm)r{\omega ^2}......(1)$
Since total mass of ring is $m$ and total length of ring is $2\pi r$ hence we can write
$dm = \dfrac{m}{{2\pi r}}(2dr) = \dfrac{m}{{2\pi }}(2\theta )$
Hence equation (1) becomes
$F = \left( {\dfrac{{2m}}{{2\pi }}\theta } \right)r{\omega ^2}$
Which on further simplification gives
$F = \theta \dfrac{{mr{\omega ^2}}}{\pi }......(2)$
Now on resolving the component of tension we can see that the $T\cos \theta $ components cancels out and we are left with only $T\sin \theta $ components which gives the required centripetal force.
Hence we can write
$F = 2T\sin \theta $
For small $\theta $ we have $\sin \theta \approx \theta $
Hence we have left with,
$F = 2T\theta ......(3)$
Now equating equation (2) and (3) we get
$2T\theta = \dfrac{{\theta mr{\omega ^2}}}{\pi }$
Now on simplification we get,
$T = \dfrac{{mr{\omega ^2}}}{{2\pi }}$

Hence option (D) is correct.

Note: It should be kept in mind that the centripetal force is another word for force toward center. This force must originate from some external source such as gravitation, tension, friction, Coulomb force, etc. Centripetal force is not a new kind of force just as an upward force or downward force is not a new kind of force.