Question

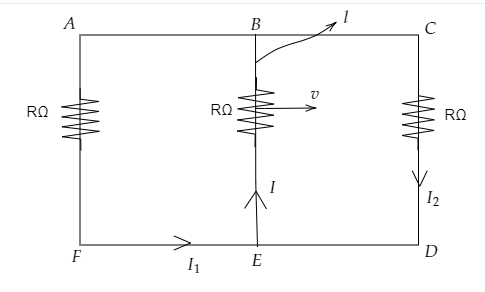
A rectangular loop has a sliding connector $BE$ of length $l$ and resistance $R\Omega$, and it is moving with a speed of $v$ as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The currents ${{I}_{1}}$, ${{I}_{2}}$ and $I$ are:

A) ${{I}_{1}}={{I}_{2}}=\dfrac{Blv}{R},I=\dfrac{2Blv}{R}$
B) ${{I}_{1}}={{I}_{2}}=\dfrac{Blv}{3R},I=\dfrac{2Blv}{3R}$
C) ${{I}_{1}}={{I}_{2}}=I=\dfrac{Blv}{R}$
D) ${{I}_{1}}={{I}_{2}}=\dfrac{Blv}{6R},I=\dfrac{Blv}{3R}$

Answer 1

Hint: Suppose a wire is placed in a magnetic field and goes through the relative motion with respect to the magnetic field, then the charges at rest in the wire experience a force by the magnetic field. This force is the charge times the cross product of the velocity of the wire and the magnetic field, i.e., $\vec{F}=q(\vec{v}\times \vec{B})$.
If the wire is stationary, it has zero velocity; hence it does not experience any force.

Complete step by step solution:
Due to the force exerted and work done by the magnetic field on the charges of the wire, the charges are set into motion inducing an electric current in the wire. The work done by the magnetic field acts as if some voltage or potential difference (or electromotive force) is applied across the wire.
Work done $(W)$ = force $(\vec{F}=q(\vec{v}\times \vec{B}))$ $\times$ displacement
Work done per unit charge on a wire of length $l$ such that displacement of the charges is $l$ is given by:
$\Rightarrow \dfrac{W}{q}=l.(\vec{v}\times \vec{B})$
$\therefore emf=Voltage=lvb\sin {{90}^{\circ }}=Blv$
Applying Kirchhoff’s first law, namely, Kirchhoff’s Current law at the node $E$,
$I={{I}_{1}}+{{I}_{2}}$………………….. Equation (1)
Applying Kirchhoff’s second law, namely, Kirchhoff’s Voltage law;
In loop AFEBA,
${{I}_{1}}R+IR-vBl=0$…………… equation (2)
In loop BCDEB,
${{I}_{2}}R+IR-vBl=0$…………………….equation (3)
Adding equations (2) and (3);
$\Rightarrow 2IR+({{I}_{1}}+{{I}_{2}})R=2vBl$
Substituting the value of $({{I}_{1}}+{{I}_{2}})$ from equation (1):
$\Rightarrow 2IR+IR=2vBl$
$\Rightarrow 3IR=2vBl$
$\therefore I=\dfrac{2vBl}{3R}$
Further substituting the value of $I$ in equation (2) to find the value of ${{I}_{1}}$:
$\Rightarrow {{I}_{1}}R+(\dfrac{2vBl}{3R})R=vBl$
$\Rightarrow {{I}_{1}}R=vBl-\dfrac{2vBl}{3}$
$\therefore {{I}_{1}}=\dfrac{vBl}{3R}$
Now, substituting the value of $I$ and ${{I}_{1}}$ in equation (1) to find ${{I}_{2}}$:
$\Rightarrow \dfrac{2vBl}{3R}=\dfrac{vBl}{3R}+{{I}_{2}}$
$\Rightarrow {{I}_{2}}=\dfrac{vBl}{3R}$

Therefore, the correct answer is [B], ${{I}_{1}}={{I}_{2}}=\dfrac{Blv}{3R},I=\dfrac{2Blv}{3R}$.

Note: Kirchhoff’s Current law states that the total current entering at a node is equal to the total current exiting the node, and Kirchhoff’s voltage law states that the sum of voltages around a loop is zero. The direction of the force is given the Flemings’ Left-hand rule.