Question

A point source of light ‘S’ is placed at l distance normally to the plane mirror of length ‘d’. A man is moving parallel to the plane mirror at ‘2l’ distance. To what length, the man can see the image of the light source inside the mirror.

Answer 1

Hint: For a man to see the reflection of the light, he must be within the range of the reflected rays from the mirror. By drawing the ray diagram of the reflection of light from a plane mirror, we can find this coverage region by using the property of similarity of triangles, which states that corresponding parts of similar triangles have the same ratio.

Complete step by step answer:
Consider a point source of light ‘S’ placed in front of a mirror at a distance of ‘L’.


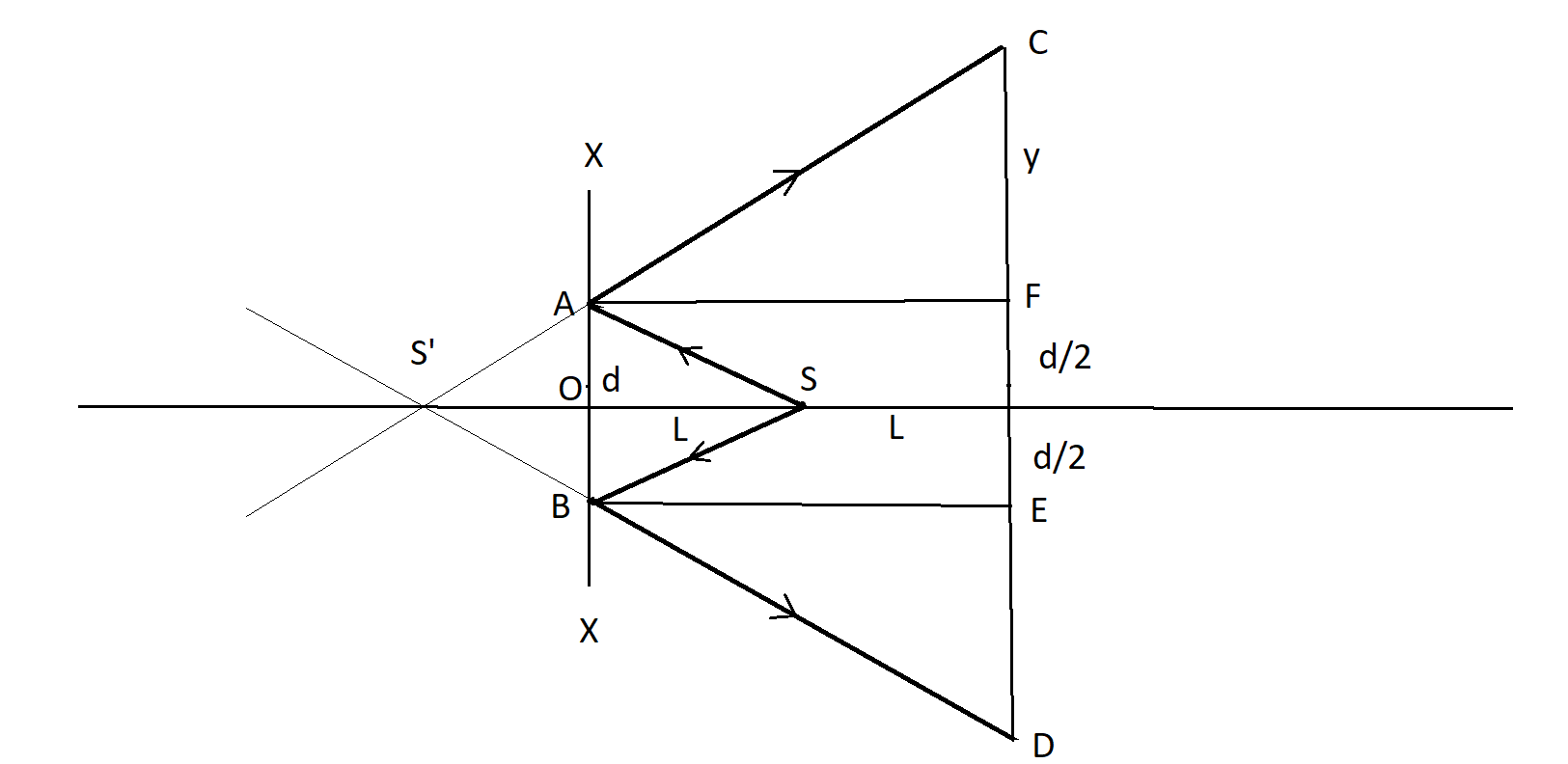
The two extreme end rays of the diverging point source S, strike the mirror at the points A and B, which are separated by a distance of d.
After reflection, they travel in another direction and meet the line at C and D where the man is starting, at a distance of 2L from the mirror.
$S'$ is an image produced by the light source S.
The man starts walking at point C which is at distance y from the point F.
Consider the triangles ACF and $AOS'$
$\angle OSA = \angle FAC$ (Vertically opposite angles)

As per the law of reflection, incident angle $\angle SAF$ is equal to the reflected angle $\angle FAC$.
Since the line FA is parallel to the axis of the mirror, $\angle FAC = \angle AS'O$ due to the property of transverse line cutting two parallel lines.

Since two angle pairs are equal, we can prove the similarity of the triangles.
$\Delta ACF \sim \Delta AOS'$

So, by the rule of corresponding angles of similar triangles are in equal ratios, we have –
$\dfrac{y}{{2L}} = \dfrac{d}{{2L}}$
$ \Rightarrow y = d$
Now, that we have the relation between y and d, we can deduce the length of the line CD.
$CD = y + y + \dfrac{d}{2} + \dfrac{d}{2}$
Substituting y =d, we have –
$CD = d + d + \dfrac{d}{2} + \dfrac{d}{2}$
$CD = 3d$
where d is the distance between two extreme points where the point source S hits the mirror.

In conclusion, the man can see the reflection of the light source up to 3 times the distance between the points where the extreme end rays of the light source hit the mirror surface.

Note: This problem gives us an understanding of a concept that if a point light source is reflected off a mirror, it can cover only 3 times the distance between the extreme end ray points. This is a very low number and hence, plane mirrors cannot be used as reflective surfaces in lighting instruments such as street-bulbs or torches. However, if we use a curved mirror in place of the plane mirror, the coverage is more than 10 times the above said distance.