Question

A monkey is at rest on a weightless rope which goes over a pulley and is tied to a bunch of bananas at the other end. The weight of the bunch of bananas is exactly the same as that of the monkey. The pulley is frictionless and weightless. The monkey starts to climb up the rope to reach the bananas. As he climbs, the distance between him and the bananas will:

$\left(A\right)$ Decrease
$\left(B\right)$ Increase
$\left(C\right)$ First decrease and then increase
$\left(D\right)$ Remain unchanged

Answer 1

Hint: Here, the monkey accelerates upwards, thus the bunch of bananas also accelerates with the same magnitude which is downwards. The mass of the monkey and bananas are the same. The separation between monkey and bananas remains constant. In case the monkey moves upward then $$T>MG$$.

Complete step by step answer:

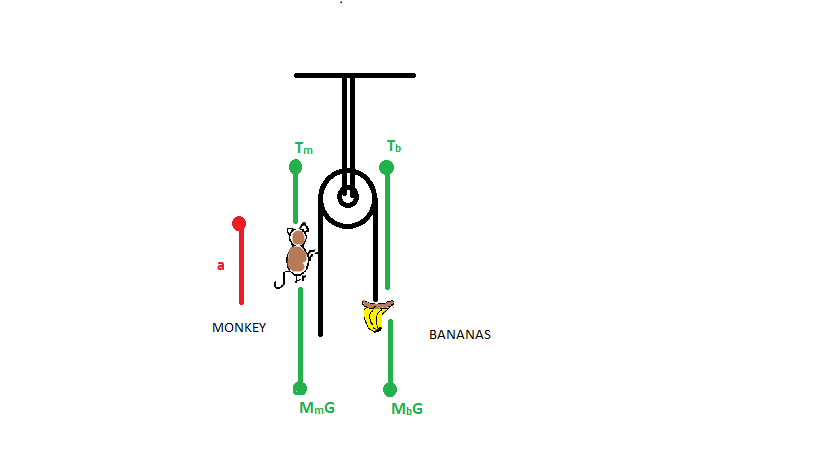
Let us assume that the monkey is moving upward with direction a. The forces acting on the monkey is $$M_{m}G$$ and tension $$T_m$$ because of the rope.
Similarly, the forces acting on the bananas are $$M_{b}G$$ and tension $$T_b$$ because of the rope.
So, from the above data the net force in the direction of acceleration a (for monkey) is:
$$\Rightarrow T=M_m(G+a)$$
The net force for bananas is
$$\Rightarrow T=M_{b}G$$
Equating both the equations,
$$\Rightarrow M_{b}G=M_m(G+a)$$
On multiplying the term we get
$$\Rightarrow M_{b}G=M_{m}G+M_{m}a$$
According to the question, the mass of the monkey and bananas are the same.
So, $$M_m=M_b$$
$$\Rightarrow M_{m}a=0$$
$$\Rightarrow a=0$$.
Therefore, the acceleration $$a$$is zero and the distance between monkey and the banana will remain unchanged.

Hence the correct option is $$D$$.

Note: In the above question, bananas are not accelerating in any direction and only the monkey is moving with an acceleration a.
Wrong thinking:
The monkey is moving up by pulling the rope downwards, then the distance between the monkey and bananas will be decreased.
The above one is wrong because the masses of the monkey and bananas are the same as per question.