Question

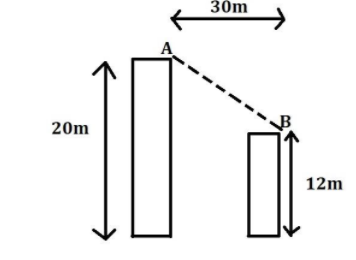
A boy wants to throw a ball from a point \[A\] so as to just clear the cliff at \[B\]. The minimum horizontal velocity with which the body should throw the ball is $(g = 10\;{\text{m}}/{{\text{s}}^2})$

(A) \[2.4m/s\]
(B) \[23.8m/s\]
(C) \[238m/s\]
(D) \[47.4m/s\]

Answer 1

Hint: Let us suppose a ball is thrown downwards from the edge of a cliff at an initial velocity \[u\] \[m/s\]. We know that the ball would be under the effect of gravity and would be having a positive acceleration. To find out the velocity with which the boy should throw the ball, we have to apply the equation of kinematics.
Formula Used: We will be using the following formula,
\[u = \dfrac{S}{{\sqrt {\dfrac{{2({h_1} - {h_2})}}{g}} }}\]
Where
\[u\] is the required velocity
\[S\] is the distance between the cliffs
\[{h_1}\] is the height of the taller cliff
\[{h_2}\] is the height of the shorter cliff
\[g\] is the acceleration due to gravity

Complete Step-by-Step Solution:
According to the question, the following information is provided to us:
The height of the taller cliff, \[{h_1} = 20m\]
The height of the shorter cliff, \[{h_2} = 12m/s\]
The distance between the cliffs, \[S = 30m\]
And the acceleration due to gravity, \[g = 10m/{s^2}\]
Now we will put all these values provided to us in the above formula to find out the required velocity
So, we get
\[u = \dfrac{S}{{\sqrt {\dfrac{{2({h_1} - {h_2})}}{g}} }}\]
\[ \Rightarrow u = \dfrac{{30}}{{\sqrt {\dfrac{{2(20 - 12)}}{{10}}} }}\]
Upon further solving, we get
\[\therefore u = 23.80m/s\]

Hence, the correct option is (B.)

Note: Kinematic equations are a set of four equations that can be used, if other information is known, to predict unknown information about the motion of an object. For any motion that can be described as being either a constant velocity motion or a constant acceleration motion, the equations can be used. Over any time period during which the acceleration changes, they can never be used. Four variables are part of each of the kinematic equations. The value of the fourth variable can be calculated if the values of three of the four variables are known.