JEE Advanced 2025 Revision Notes for Mechanics - Free PDF Download
Physical Quantities
A quantity that we can measure is termed a Physical Quantity.
A physical quantity shall have a numeric value or magnitude which can represent the exact amount of the object to be measured.
For e.g. length can be measured in metres, the mass of an object can be measured in Kgs and so on.
Physical Quantities are Divided Into Two Types:
Fundamental Quantities
Derived Quantities
Physical Quantities
Units
To estimate the size or to measure a physical quantity, we need a reference point or a reference standard. This point of reference is called a Unit of the given physical quantity.
Units are Divided Into Two Types:
Fundamental units
Derived units
Fundamental Units: The unit which gives an idea of the amount or size of the fundamental Quantities are called Fundamental Units.
Derived Units: The units which give an idea of the amount or size of the Derived Quantities are called Derived Units.
e.g., Let us consider the unit of speed.
$\text { speed }=\dfrac{\text { distance travelled }}{\text { time taken }}$
$\therefore \quad$ Unit of Speed $=\dfrac{\text { unit of distance }}{\text { unit of time }}=\dfrac{\text { metre }}{\text { second }}=\mathrm{ms}^{-1}$
Thus, the unit of speed is derived from fundamental units of length, mass and time.
System of Units
A collection of units which can be used to measure all fundamental and derived quantities is called a system of units. Some of the most accepted systems of units are given as follows:
CGS System
The Centimetre-Gram-Second (CGS) System is also called the Gaussian System of Units. In this system we use centimetre (cm) as unit of length, gram (g) as unit of mass, and second(s) as unit of time.
For Example: Dyne is used as the unit of force in CGS system.
FPS System
The Foot-Pound-Second (FPS) System is a British Engineering System of units. In this system we use foot (ft) as unit of length, pound (lb) as unit of mass, and second(s) as unit of time.
For Example: Poundal (pdl) is used as the unit of force in FPS system.
MKS System
In the Metre-Kilogram-Second (MKS) System of units, we use metre(m) as unit of length, kilogram(kg) as unit of mass, and second(s) as unit of time.
Newton is used as the unit of Force.
International System of Units
The International System of Units generally called S.I. units is the latest form of the metric system. The S.I. system consists of seven fundamental units and two supplementary units stated below:
Fundamental Unit
Supplementary Unit
Unit Conversions (Length)
The length is measured in terms of metre as per the SI system, but it gets complicated to denote very small and very large distances in metre, e.g., the radius of an electron, the distance of the nearby galaxy from earth. All these distances are huge in terms of sheer numbers. So to make it easy, some conversions are followed:
Units to measure small distances:
$1 \mathrm{~cm}=10^{-2} \mathrm{~m}$
$1 \mathrm{~mm}=10^{-3} \mathrm{~m}$
1 micron $(\mu)=10^{-6} \mathrm{~m}$
1 nanometre $(\mathrm{nm})=10^{-9} \mathrm{~m}$
1 angstrom $(AA)=10^{-10} \mathrm{~m}$
1 fermi $=10^{-15} \mathrm{~m}$
Dimensions of Physical Quantity
Dimensions of a physical quantity can be defined as the powers to which the fundamental quantities are raised to describe the unit of that physical quantity.
The elementary physical dimensions are: length, time, mass, electric current, temperature, amount of substance and luminous intensity.
For example, the volume occupied by an object is expressed as the product of length, breadth and height, or three lengths. Hence the dimensions of volume are $[\mathrm{L}] \times[\mathrm{L}] \times[\mathrm{L}]=[\mathrm{L}]^{3}=\left[\mathrm{L}^{3}\right]$. As the volume is independent of mass and time, it is said to possess zero dimension in mass $[\left.\mathrm{M}^{\circ}\right]$, zero dimension in time $[ \left.\mathrm{T}^{\circ}\right]$ and three dimensions in length. Similarly, velocity can be written as
$v=\dfrac{\text { length }}{\text { time }}$
The dimensions of velocity are $\dfrac{\left[ {{M}^{0}} \right]\text{ }\left[ L \right]\text{ }}{\left[ T \right]}$= \[\left[ {{M}^{0}}L{{T}^{1}} \right].\] Thus, the velocity has one dimension in length, -1 dimension in time, and zero dimensions in mass. The dimensions in all other base quantities are zero.
Dimensions of Fundamental Quantities
Dimensional Formula
The expression which shows how and which of the base quantities represent the dimensions of a physical quantity is called the dimensional formula of the given physical quantity. For example, the dimensional formula of the density is $\left[\mathrm{ML}^{-3} \mathrm{~T}^{\circ}\right]$, and that of force is $\left[\mathrm{MLT}^{-2}\right]$.
Dimensional Formulae and Si Units of Some Basic Physical Quantities
Motion in One Dimension:
Distance: Distance is basically the path length travelled by a body. Distance is a scalar quantity; it has no fixed direction.
Displacement: Displacement is defined as the minimum distance between two points, which means displacement is always defined along a straight line and has a fixed direction. Displacement is a vector quantity. The magnitude of displacement is independent of the path travelled by a body. It is only dependent on the initial and final points.
Speed and Average Speed: Speed is the defined as the rate at which a body travelled through a path. Average speed is the mean distance travelled in unit time. As speed has no fixed direction, it is a scalar quantity.
Velocity and Average Velocity: Velocity is the rate of change of displacement. Average velocity is the change in position or displacement divided by the time interval in which the displacement occurs.
Acceleration: Acceleration is the rate of change of velocity. It is a vector quantity.
Distance
Any object that moves in one direction or another is defined as a distance. Distance is simply the amount of ground an object has covered, regardless of its starting or ending point. Distance is a scalar quantity since its magnitude determines its value, not its direction.
Distance can only have a positive value.
Distance Formula $\Delta d=d_{1}+d_{2}$
Displacement
The displacement of an object is defined as the change in its position. Vector quantities have magnitude and direction. The arrow indicates the position of the starting point and the final position.
For example: A position changes if an object moves from A to B. An object's displacement is its change in position.
Displacement is a vector quantity since its magnitude and direction are both influenced by it.
The displacement can be positive, negative, or even zero.
Displacement $=\Delta x=x_{f}-x_{0}$
$x_{f}=$ Final Position
$x_{0}=$ Initial Position
$\Delta x=$ Displacement
Speed:
The speed of an object is defined as the distance travelled per unit of time.$\text { Speed }=\dfrac{\text { Distance travelled }}{\text { Time taken }}$
The following are the several types of speed:
Uniform Speed:
If an object covers equal distances in equal intervals of time, it is said to be moving uniformly.
Non-Uniform Speed:
Non- uniform speed is the speed in which the distance covered by the object is not equal in equal intervals of time.
Average Speed:
The average speed of an object is equal to the distance travelled divided by the time taken.
Average speed $=\dfrac{\text { Total distance travelled }}{\text { Total time taken }}$$=\dfrac{s_{1}+s_{2}+s_{3}+\ldots}{t_{1}+t_{2}+t_{3}+\ldots}$ where $s_{1}, s_{2}, s_{3} \ldots \ldots$ are the distances travelled by the object with speed $v_{1}, v_{2}, v_{3} \ldots$ respectively.
If an object travels the same distance at the same speed $v_{1}$ and $v_{2}$, then average speed $=\dfrac{2 v_{1} v_{2}}{v_{1}+v_{2}}$
Objects that cover the first third of the distance with speed $a$, other one-third distance with speed $b$ and last one-third distance with speed $c$, then average speed $=\dfrac{3 a b c}{a b+b c+c a}$
Instantaneous Speed:
The speed of an object at a given instant of time is called its instantaneous speed when the object is traveling with variable speed.
Instantaneous speed $=\lim _{\Delta t \rightarrow 0} \dfrac{\Delta s}{\Delta t}=\dfrac{d s}{d t}$
Acceleration:
The acceleration of an object is the rate at which its velocity changes over time.
Acceleration $(a)=\dfrac{\text { Change in velocity }}{\text { Time taken }}$
It is a vector quantity.
Types of acceleration are given below
Uniform Acceleration:
If an object's velocity changes by equal amounts in equal intervals of time, it is said to be moving with uniform acceleration.
Non-Uniform Acceleration:
If an object's velocity changes by unequal amounts in equal intervals of time, it is said to be moving with a non-uniform or variable acceleration.
Average Acceleration If a body travels with uniform acceleration $a_{1}$ and $a_{2}$ in time $t_{1}$ and $t_{2}$, respectively, The average acceleration can then be expressed as $a=\dfrac{a_{1} t_{1}+a_{2} t_{2}}{t_{1}+t_{2}}$.
Instantaneous Acceleration:
Instantaneous acceleration refers to acceleration that occurs at any given time.
i.e. $\quad a=\lim _{\Delta t \rightarrow 0} \dfrac{\Delta v}{\Delta t}=\dfrac{d v}{d t}$
If an object's velocity decreases over time, it has a negative acceleration; otherwise, it has a positive acceleration.
Retardation or decelerations are other terms for negative acceleration.
An object's velocity and acceleration don't have to be zero at the same time.
Equations for One-Dimensional Motion:
Consider an object moving at a constant velocity in a straight line path. $(u)$ and after time $t$ its velocity changes to $(v)$, if the uniform acceleration is $(a)$ and the distance travelled by the object in time $(t)$ is (s), The following equations of one-dimensional motion are obtained as a result of this process.
$v=u+a t$
$s=u t+\dfrac{1}{2} a t^{2}$
$v^{2}=u^{2}+2 a s$
(a). If an object starts from rest, then $u=0$.
(b). If an object comes to rest (i.e. it stops), then$v=0$.
(c). If an object moves with uniform velocity, then its acceleration,$a=0$.
Relative Motion:
When we travel on a train and another train moving in the same direction passes by, it does seem slower to you than it would be to someone standing on the ground and watching both of the trains. If both of the trains have the same velocity with respect to the ground, then to you, the other train would seem to be at rest.
Frame of Reference:
A reference frame is a coordinate system in which an event is depicted.
Types of Reference Frames:
Inertial Frame of Reference: These frames are at rest with each other or which are moving with a uniform speed with respect to each other.
Non-inertial Frame of Reference: All accelerated and rotatory reference frames are non-inertial frames of reference. Newton’s law does not hold good in the non-inertial reference frame.
Linear Momentum:
Inertia:
Inertia is a property of matter that causes it to resist changes in velocity.
Any object remains in the state of rest or in a uniform Motion along a straight line until it is compelled to change the state by applying an external force.
This law as also known as Law of Inertia.
Tips: How to find causes of the motion of a body which is initially in the state of rest.
First apply the first law of motion.
Now check the options by putting law.
Now if only one option matches then that option is correct, if not then hop on to the other options.
Impulse
A large force which acts on an object for a very short interval of time and produces a large change in its momentum is called an impulsive force.
The impulse of a force acting on an object is equal to the product of the large force and small-time interval for which its acts on the object.
Impulse $(I)=$ Force $\times$ Time
Its unit is Newton second.
Newton’s Laws of Motion:
First Law: According to Newton’s first law, a body continues to be in a state of rest or of uniform motion until it is acted upon by some external force to change its state (from rest to motion or from motion to rest).
Second Law: According to Newton’s second law, the rate of change of momentum of a body is directly proportional to the external force applied on it, and the change takes place in the direction of force applied. The force on a body of mass m having acceleration a is given by F = ma.
Third Law: Newton’s third law states that to every action, there is an equal and opposite reaction.
Types of Forces:
Electromagnetic Force: This is the interaction force between bodies due to presence of charge.
Gravitational Force: This is the interaction force between masses according to the universal gravitational law.
The Weak Force: The weak force is responsible for processes of transformations of particle.
The Strong Force: The strong force acts only when subatomic particles are extremely close to one another.
Friction:
When the surface of a body slides over another, each of the body experiences a contact force that always opposes the relative motion between the surfaces of the bodies called frictional force.
Direction of Friction:
Since friction opposes the relative motion between two bodies, it always acts in a direction opposite to that of the actual motion.
Static Friction:
Static friction is the force of friction between two surfaces as long as there is no relative motion between them. For a body, at rest, the maximum static frictional force is always equal to the applied force.
Kinetic Friction:
Kinetic friction is the force of friction that acts between two surfaces when there is some relative motion between them.
Work
When an object is compelled to move from one spot to another, work is accomplished. Work is equal to force multiplied by displacement. Determining how far a body travelled is termed displacement.
If the force F and the displacement d are both in the same direction, the work W can be calculated using the formula,\[W\text{ }=F\times d\]
Work is equal to the product of displacement and force. In SI (international system) units, unit of the force is Newton (N), And the distance & displacement unit is the metre (m)
A Newton-meter can thus be used to express the work unit. It's also known as a Joule, or J. Because the Newton is a composite unit, a Joule is also comparable to it.$1~\text{J}=1~\text{N}\cdot \text{m}=1~\text{kg}\cdot \dfrac{{{\text{m}}^{2}}}{~{{\text{s}}^{2}}}$
The equation \[W\text{ }=F\times d\]depends on the same direction as force and displacement.
There are a variety of situations where, for example, someone pushing on a box near the floor is moving in a specific direction.
Although the box's resulting direction is forward, a portion of the force is directed down. In a case like this, only the force along the route of the displacement contributes to the job being done. If we treat force and displacement as vectors, then we can find the work by using the dot product (also known as the scalar product).
$W=\vec{F}\cdot \vec{d}$
$W=Fd\cos \theta $
In above formula, θ is the angle between the force and displacement vectors, and F and d are the magnitudes of the vectors.
When work is performed against gravity, the amount of work performed equals the body's weight product plus the vertical distance lifted.
Work done in lifting body = Weight of Body$\times $ Vertical Distance
\[W=mgh\]
Where, W = Work Done
M = Mass of body, g = acceleration due to gravity,
h = Height through which the body is lifted
The quantity of work is a scalar quantity. Joule is the SI unit of work, and erg is the CGS unit of work.
$\therefore 1$ Joule $={{10}^{7}}\text{erg}$
Its dimensional formula is $\left[ \text{M}{{\text{L}}^{2}}~{{\text{T}}^{-2}} \right]$.
Work done by a force is zero, if
Body is not displaced actually, i.e., $s=0$.
The body is shifted perpendicular to the force direction. i.e., $\theta ={{90}^{{}^\circ }}$.
When the angle between F and s is acute, the work done by a force is positive.
If the angle between F and s is obtuse angle, the work done by the force is negative.
The work done by a constant force is dependent only on the initial and final places, not on the actual path taken between them.
Power
Power is a measure of work rate. It is a measurement of how fast work is performed. For a quantity of work W performed in time t, the power performed is $P=\dfrac{W}{t}$.
The Power unit is the Watt (W), which equals one Joule per second. 1 W = 1 J/s
Power P can also be expressed as force F times velocity v. Since work is provided by force times displacement, \[W\text{ }=\text{ }F\times d\], then we know that, $P=\dfrac{W}{t}$
$\therefore P=\dfrac{(Fd)}{t}$
$\therefore P=F\left( \dfrac{d}{t} \right)$
$\therefore P=Fv$
Power is a scalar quantity. Its SI unit is watt and its dimensional formula is $\left[ \text{M}{{\text{L}}^{2}}~{{\text{T}}^{-3}} \right]$.
Its other units are kilowatt and horse power,
1 kilowatt $=1000$ watt
1 horse power $=746$ watt.
Energy
Energy is the ability of a body to perform work. Energy is a scalar quantity, which means it has simply magnitude and no direction.
The joule is the S.I unit, while the erg is the CGS unit. Its dimensional formula is as follows: \[\left[ M{{L}^{3}}{{T}^{-3}} \right].\]
Mechanical energy (kinetic and potential energy), chemical energy, light energy, heat energy, sound energy, nuclear energy, electric energy, and other types of energy exist.
Potential Energy:
The energy associated with the configuration of a system in which conservative force acts is called potential energy.
Kinetic Energy:
The energy possessed by a body due to its motion is called kinetic energy of the body.
Mechanical Energy:
The sum of the kinetic energy and the potential energy of a body is called mechanical energy.
Work Energy Theorem:
The net work done by all the forces on a body is equal to the change in kinetic energy of the body.
Conservation of Momentum:
If the net force on a system is zero, then its momentum is conserved.
Initial Momentum = Final Momentum when Force = 0
Coefficient of Restitution (e) and Collision:
e = 0 means Completely Inelastic Collision
0 < e < 1 means Partially Elastic Collision/Partially Inelastic Collision
e = 1 means Completely Elastic Collision
Universal Law of Gravitation (Newton's Law):
Everybody in the universe attracts every other body with a force that is proportional to the product of their masses and inversely proportional to the square of their distance. It is known as the gravitational force.
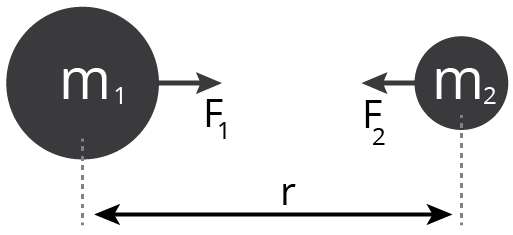
Universal Law of Gravitation
$\overrightarrow{\text{F}}\propto \dfrac{{{\text{m}}_{1}}{{\text{m}}_{2}}}{{{\text{R}}^{2}}}$
$\overrightarrow{\text{F}}=\dfrac{\text{G}{{\text{m}}_{1}}{{\text{m}}_{2}}}{{{\text{R}}^{2}}}$
Here\[{{m}_{1}}\]and \[{{m}_{2}}\] are the masses of two bodies, and here R is the distance between them and G is the Gravitational Constant. G = 6.67 × 10-11 Nm2(kg)-2
1. In nature, gravitational force is always attractive.
2. The nature of the intervening medium has no bearing on the gravitational force.
3. The gravitational force is conservative in nature.
4. Because it is a central force, it acts along a line that connects the centers of the two interacting bodies and obeys the inverse square law.
Acceleration Due To Gravity$(g)$:
When an object falls towards the earth, it experiences acceleration. This acceleration is called acceleration due to gravity or acceleration due to the gravitational force of the earth because it is caused by the earth's gravitational pull.
We know that, Acceleration due to gravity, $g=\dfrac{G{{M}_{e}}}{R_{e}^{2}}$
Here, ${{M}_{e}}=$ mass of the earth, ${{R}_{e}}=\text{ radius of the earth }$
Variation in the Value of $g$:
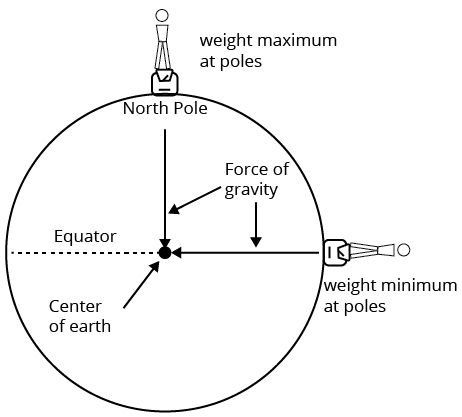
Variation in the Value of g
We know that, the value of Acceleration due to gravity (g) is maximum at poles and minimum at equator (it happens due to shape of the earth).
The observed value of $g$ at the latitude $\lambda $ is ${{g}^{\prime }}=g-{{R}_{e}}{{\omega }^{2}}{{\cos }^{2}}\lambda $
At equator, $\lambda ={{0}^{{}^\circ }},\cos \lambda =\cos {{0}^{{}^\circ }}=1,{{g}^{\prime }}={{g}_{e}}$ ${{g}_{e}}=g-{{R}_{e}}{{\omega }^{2}}$
At pole, $\lambda ={{90}^{{}^\circ }},\cos x=0,{{g}^{\prime }}={{g}_{p}}$
Along the Surface of the Earth
The earth does not have a perfect spherical shape.
Due to its rotation, it bulges at the equator and flattens at the pole.
The equator has the largest radius, while the poles have the smallest.
Value of $\text{g}$ is highest at poles $\left( 9.832~\text{m}/{{\text{s}}^{2}} \right)$
Value of $g$ is least at equator $\left( 9.78~\text{m}/{{\text{s}}^{2}} \right)$
Change with Height
Because the value of g is inversely proportional to the height above the earth's surface, it decreases as the height rises.
For heights less than the earth's radius, the change is negligible.
Change with Depth
Because the value of g is proportional to the depth beneath the earth's surface, it rises with depth but falls to zero at the earth's center.
This is because the mass under consideration decreases as we travel deeper into the earth. Then value of $g$ decreases.
Hence, the value of $g$ at depth $d$ below the earth's surface decreases, ${{g}^{\prime }}=g\left( 1-\dfrac{d}{{{R}_{e}}} \right)$
Escape Velocity:
The minimum velocity at which a body must be projected vertically upwards in order to escape the earth's gravitational field is called escape velocity.
Escape velocity, ${{v}_{e}}=\sqrt{2gR}$
The value of escape velocity on the earth's surface is $11.6~\text{km}/\text{s}$.
Relation between orbital velocity of a satellite and escape velocity is ${{v}_{e}}=\sqrt{2}{{v}_{o}}$
Mass and Weight:
A body's mass is a measure of its inertia; the greater the mass, the greater the inertia.
A body's weight is equal to the product of its mass and the gravitational acceleration at that location.$w=mg$.
A body's mass remains constant, but its weight varies slightly from place to place on the planet.
At the poles, a body's weight is greatest, while at the equator, it is smallest.
Weight of a Body in Elevator or Lift:
When a person (or any other body) is inside an accelerating lift, there is a change in weight known as apparent weight, which is followed by a set of conditions.
When a lift ascends with an upward acceleration or descends with a downward deceleration, the body perceives an increase in weight.
When a lift descends with a downward acceleration or ascends with an upward deceleration, the body perceives a reduction in weight.
When a lift moves downward at the same rate as gravity, the body experiences weightlessness.
Weight of a Body at the Moon:
Because the moon's mass and radius are smaller than the earth's, its gravitational force is also smaller. Its value at the moon's surface is $\dfrac{g}{6}$.
Projectile Motion:
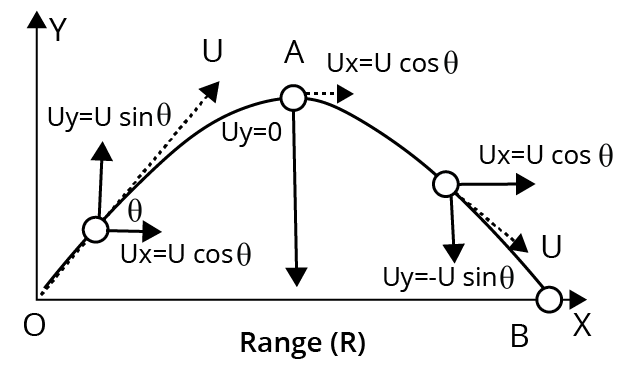
Projectile Motion
If a particle is thrown obliquely near the surface of the earth, it travels along a curved path while accelerating continuously in the direction of the planet's centre (we assume the particle stays close to the surface of the globe). Such a particle's motion is known as projectile motion, and its route is referred to as a projectile.
Acceleration of a particle's projectile motion, both horizontally and vertically: When a particle is sent into the air at a certain speed, the only force acting on it is the acceleration caused by gravity (g). This downward vertical acceleration has an effect. The fact that there is no acceleration in the horizontal direction means that the particle's horizontal velocity stays constant.
The projection point is designated as O; the projection angle is denoted by ; and OB stands for horizontal range or simply range. The time of flight is the length of time the particle needs to go from point O to point B.
We can utilise differential equations of motion to determine various projectile motion parameters:
(1) $\mathbf{v}=\mathbf{u}-\mathbf{g t}$
(2) $s=u t-\dfrac{1}{2} g t^{2}$
(3) $v^{2}=u^{2}-2 g s$
$\mathrm{u}=$ Initial velocity $\text{,g}=$ Acceleration due to gravity $\mathbf{t}=$ Time $,\text{s}=$ Displacement $,\text{v}=$ Final velocity
Total Time of Flight: Total Time of Flight $(t)=\dfrac{2u\sin \theta }{g}$
Horizontal Range: Horizontal Range $(R)=\dfrac{{{u}^{2}}\sin 2\theta }{g}$
Maximum Height of Projectile: $H=\dfrac{v_{0}^{2} \sin ^{2} \theta}{2 g}$
The Equation of Trajectory: Equation of Trajectory $=x\tan \theta -\dfrac{g{{x}^{2}}}{2{{u}^{2}}{{\cos }^{2}}\theta }$
Wave
A wave is a vibratory disturbance in a medium which carries energy from one point to another point without any actual movement of the medium.
There are mainly three types of waves
Mechanical Waves The waves which can be propagated or produced only in a material medium, are called mechanical waves.
Electromagnetic Waves The waves which require no medium for their propagation or production are called electromagnetic waves.
Matter Waves The waves associated with moving particles like electrons, protons, etc, are called matter waves.
Types of Mechanical Waves:
Mechanical waves are of two types
Longitudinal Waves
A wave in which the particles of the medium vibrate in the same direction of propagation of wave is called longitudinal wave.
Longitudinal waves can be produced in all the three media such as solids, liquids and gases.
The waves which are produced in air are always longitudinal. e.g., those waves which travel along a spring when it is pushed and pulled at one end, are longitudinal waves.
Spring
When coils are closer to each other than normal, compressions are observed in the spring.
When coils are farther apart than normal, rarefactions are observed.
A long feasible spring which can be compressed or extended easily, is called slinky.
When a longitudinal wave passes through air, the density of air changes continuously and the pressure and energy are being transferred.
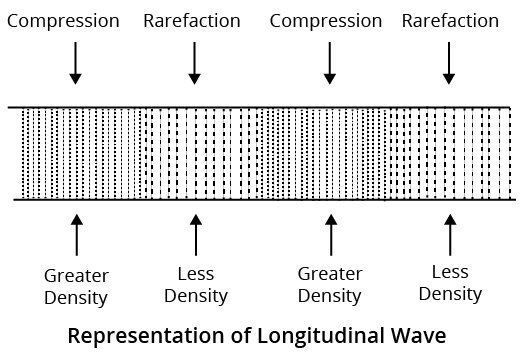
Representation of longitudinal waves
Transverse Waves
A wave, in which the particles of the medium vibrate perpendicular to the direction of propagation of the wave, is called a transverse wave.
Transverse waves can be produced only in solids and liquids.
Light is a transverse wave but it is not a mechanical wave.
The waves produced by moving one end of long spring or rope up and down rapidly and whose other end is fixed, are transverse waves.
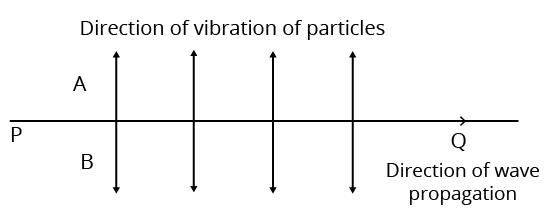
Direction of Vibration of Particles
The water waves (or ripples) formed on the surface of water in a pond (when a stone is dropped in the pond of water), are transverse waves.
A transverse wave travels horizontally in a medium and the particles of the medium vibrate up and down in the vertical direction. In transverse waves, crest and trough are formed.
A crest is that part of the transverse wave which is above the line of zero disturbance of the medium. A trough is that part of the transverse wave which is below the line of zero disturbances.
A transverse wave has been represented by a displacement-distance graph as shown below
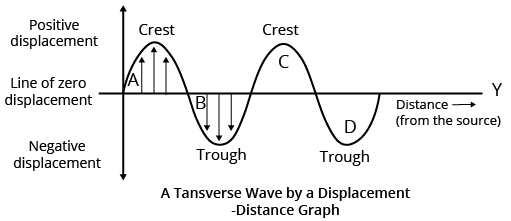
Transverse wave
Wave Motion
When a large number of particles vibrate simultaneously in a medium, then disturbance propagates in the medium.
The motion of disturbance is called wave motion. Energy of momentum is transferred to the neighboring particles of the medium as wave proceeds.
Some Definitions Related To Wave Motion
Amplitude It is the maximum displacement suffered by the particles of the medium about their mean positions. It is denoted by $A$.
Time Period The time period of a wave is the time in which a particle of medium completes one vibration to and fro about its mean position. It is denoted by$T$.
Frequency The frequency of a wave is the number of waves produced per unit time in the given medium. It is equal to the reciprocal of the time period $T$ of the particle and is denoted by$n$. Thus $n=\dfrac{1}{T}$ . S.I unit of $n$ is ${{\text{S}}^{-1}}$ or hertz $(\text{Hz})$
Angular Frequency The rate of change of phase with time is called angular frequency of the wave. It is denoted by $\omega $. Thus $\omega =\dfrac{2\pi }{T}=2\pi n$. SI unit of $\omega $ is rad ${{\text{S}}^{-1}}$
Wavelength The distance between two nearest particles of the medium which are vibrating in the same phase. It is denoted by $\lambda $.
Wave Number The number of waves present in a unit distance of the medium is called wave number. It is equal to the reciprocal of wavelength $\lambda $.Thus, Wave number, $\bar{v}=\dfrac{1}{\lambda }$ .SI unit of wave number is ${{\text{m}}^{-1}}$.
Angular wave number of propagation constant The quantity $\dfrac{2\pi }{\lambda }$ is called angular wave number or propagation constant of a wave. It represents phase change per unit path difference. It is denoted by$K$. Thus$K=\dfrac{2\pi }{\lambda }$. The SI unit of $K$ is radian per meter or rad${{\text{m}}^{-1}}$.
Wave velocity or phase velocity The distance covered by a wave per unit time in its directions of propagation is called its wave velocity or phase velocity. It is denoted by$v$.
Relation Between Wave Velocity, Frequency and Wavelength
Wave velocity $=\dfrac{\text{ Distance }}{\text{ Time }}$
$v=\dfrac{\lambda }{T}\text{ or }v=n\lambda \quad \left\{ \because n=\dfrac{1}{\lambda } \right\}$ i.e, Wave velocity = Frequency $\times $ Wavelength
Sound
Sound is a form of energy, which produces the sensation of hearing. These are longitudinal mechanical waves.
Sound waves have low frequency and high wavelength. Sound waves cannot travel in vacuum.
The rebouncing back of sound, when it strikes a hard surface is called reflection of sound.
The repetition of sound due to reflection of sound wave is called an echo.
According To Their Frequency Range, Waves are Divided Into the Following Categories
Audible or Sound Waves The longitudinal mechanical waves, which lie in the frequency range $20~\text{Hz}$ to $20000~\text{Hz}$ are called audible or sound waves. These waves are sensitive to human ear.
Infrasonic Waves The longitudinal mechanical waves having frequencies less than $20~\text{Hz}$ are called infrasonic waves. These waves are produced by sources of bigger size such as earthquakes, volcanic erruptions, ocean waves, elephants and whales.
Ultrasonic Waves The longitudinal mechanical waves having frequencies greater than $20000~\text{Hz}$ are called ultrasonic waves. Human ear cannot detect these waves. But certain creatures like dog, cat. bat. mosquito etc. can detect these waves.
Bat not only detect but also produce ultrasonic waves.
Intensity or Loudness
Intensity of sound at any point in space is defined as the amount of energy passing normally per unit area held around that point per unit time.
Its SI unit is watt/metre. Loudness depends on intensity of sound. Unit of loudness is bel and $\dfrac{1}{10}$ th of bel is decibel $(\text{dB})$.
Quality or Timbre of Sound
Quality is that characteristic of sound, which enables us to distinguish between sound produced by two sources having the same intensity and pitch.
It depends on harmonics and their relative order and intensity.
Pitch or Frequency
The pitch of a sound is the characteristic which distinguishes between a shrillness or graveness of sound. Pitch depends upon frequency.
A still and sharp sound has higher pitch and grave and dull sound has lower pitch.
SONAR
The acronym SONAR stands for Sound Navigation and Ranging. The SONAR is a device that uses the ultrasonic waves to measure the distances, directions and speed of objects under water.
The ultrasonic sound pulse to travel from the ship to the bottom of the sea and back to the ship. In other words, the SONAR measures the time taken by the echo to return to the ship.
Half of this time gives the time taken by the ultrasonic sound to travel from the ship to the bottom of the sea.
Some Applications of SONAR are Given
Target location for torpedoes.
Resources location for mines.
Submarine navigation.
In aircraft.
Remotely operated vehicles.
Detecting the vehicle location.
Example 1: A physical quantity $\vec{S}$ is defined as $\vec{S}=(\vec{E} \times \vec{B}) / \mu_{0}$, where $\vec{E}$ is electric field, $\vec{B}$ is magnetic field and $\mu_{0}$ is the permeability of free space. The dimensions of $\vec{S}$ are the same as the dimensions of which of the following quantity(ies)?
(A) $\dfrac{\text { Energy }}{\text { Charge } e \times \text { Current }}$
(B) $\dfrac{\text { Force }}{\text { Length } \times \text { Time }}$
(C) $\dfrac{\text { Energy }}{\text { Volume }}$
(D) $\dfrac{\text { Power }}{\text { Area }}$
Answer: B,D
Hint: The power to which the fundamental units must be elevated in order to describe a physical quantity is called its dimension. The basic quantities include mass, length, time, temperature, electric current, luminous intensity, and amount of substance.
Complete solution: Dimension of electric field $[E]=\left[M A^{-1} L T^{-3}\right]$
Dimensions of magnetic field [B]
$[B]=\left[M A^{-1} L T^{-2}\right]$
Dimensions of magnetic permebility
$\left[\mu_{0}\right]=\left[M A^{-2} T^{-2} L\right]$
$[S]=\dfrac{E B}{\mu_{0}}=\dfrac{\left[M A^{-1} L T^{-3}\right]\left[M A^{-1} T^{-2}\right]}{\left[M A^{-2} T^{-2} L\right]}=\left[M T^{-3}\right]$
Example 2: Sometimes it is convenient to construct a system of units so that all quantities can be expressed in terms of only one physical quantity. In one such system, dimensions of different quantities are given in terms of a quantity $X$ as follows: $[\text {position} ]$=$\left[X^{\alpha}\right]$ ;$[\text{ speed }]$=$\left[X^{\beta}\right]$; $[\text{acceleration}]$=$\left[X^{P}\right]$ ;$ [\text{linear momentum} ]$=$\left[X^{q}\right]$ ;$[\text{ force }]$=$\left[X^{\eta}\right]$. Then
(A) $\alpha+p=2 \beta$
(B) $p+q-r=\beta$
(c) $p-q+r=\alpha$
(D) $p+q+r=\beta$
Answer: A,B
Hint: When a system's mass is multiplied by its velocity, the result is its linear momentum, or momentum for short. The net external force is defined as the change in momentum of a system divided by the duration during which it changes, according to Newton's second rule of motion in terms of momentum.
Complete solution: $[x]=x^{\alpha} \Rightarrow \dfrac{p}{v}=\text { time }$
$[v]=x^{\beta}$
$[a]=x^{p} \Rightarrow \dfrac{v}{a}=$ time
$[p]=x^{q}$
$[F]=x^{r}$
$\Rightarrow\left(\dfrac{\text { position }}{\text { speed }}\right)=\left(\dfrac{\text { speed }}{\text { acceleration }}\right)=\left(\dfrac{p}{F}\right)$
$\Rightarrow \dfrac{x^{\alpha}}{x^{\beta}}=\dfrac{x^{\beta}}{x^{\alpha}}=\dfrac{x^{q}}{x^{r}}$
$\Rightarrow x^{\alpha-\beta}=x^{\beta-p}=x^{q-r}$
$\therefore \alpha-\beta=\beta-p=q-r$
$\alpha+p=2 \beta$
$q+p=\beta+r$
$p+q-r=\beta$
Importance of Physics Mechanics
Mechanics is the basis of physics taught at the higher secondary level of education. It comprises the basic foundation of all engineering streams that students aspire to study. In fact, the preparation for competitive engineering examinations will need to focus on this chapter considerably.
This chapter focuses on explaining the basic concepts of physics related to kinematics or the movement of bodies in a plane. The laws based on kinematics and other fundamental principles will also be explained in this chapter.
It will also explain how the laws are derived and determined using various scientific terms. All these terms will be explained with the meaning of physical quantities and their symbols used for representation.
These scientific principles will guide students to understand the concepts of other chapters. They form the basis of almost all the other chapters of Physics taught at this level. Hence, studying Mechanics JEE Advanced is very important for the preparation for JEE Advanced exam.
Benefits of Vedantu’s Mechanics Revision Notes for JEE Advanced
These revision notes are prepared by the experts with the sole motive of providing a simpler explanation of all the scientific principles related to mechanics. By referring to these notes, you will find understanding the concepts easier to comprehend.
Your preparation time will reduce to a considerable extent when you refer to these concise revision notes. The fundamental concepts have been explained and consolidated in an easier format for you to remember them properly.
Once this chapter is done, you can proceed to solve the fundamental questions given as samples in these notes. These questions will help you to evaluate your preparation level and figure out the sections where you need to work harder. Make your preparation of mechanics much better by using these notes.
Recall what you have studied before an exam using these notes. Refer to the notes anywhere anytime you want to make your study sessions more productive. You can also use these notes before an exam to remember the concepts, principles, formulas, and applications quickly.
Download Mechanics Revision Notes for JEE Advanced PDF
You can now get the free PDF version of these notes to complete your study material for this chapter. Get preparation assistance from the simplest scientific explanations of laws and terms of this chapter to revise and remember. You can learn from the simplification of all the concepts and use the techniques to recall them easily to answer fundamental questions accurately.
Common Mistakes to Avoid in Exams:
1. Not answering the question
There are two main reasons for this:
(i) Not reading the question properly, or
(ii) Wanting to answer a slightly different question.
2. Not looking at the mark scheme or the space provided
Both the mark scheme and the space provided (if there is one) will provide clues about how much the examiners are expecting to see.
3. Panicking
Faced with an exam paper, it is easy to panic, especially if your first reaction is that you are unable to answer any of the questions.
4. Failing to plan your time
Before you start writing, check the number of questions, and the amount of time you have. This will tell you roughly how long you have for each question.
5. Failing to plan your answers (particularly for essays)
In writing an essay, which includes a shorter essay-type response to a question, it is important to get the structure right. An essay usually needs to make an argument, and have a reasonable flow from start to finish. This requires planning.
6. Over-generalising
It is best to be as specific as possible in whatever you write. You should show that you understand the limits of your statements.
7. Regurgitating your teacher or tutor’s notes
This is particularly important at university, when it may well be your tutor or lecturer who is marking the paper, but it also applies elsewhere too.
8. Making basic spelling and grammar errors
It is admittedly much harder without a spell check.
Important Related Links for JEE Main and JEE Advanced
