Question

A modern grand-prix racing car of mass m is travelling on a flat track in a circular arc of radius R with a speed v. If the coefficient of static friction between the tyres and the track is ${\mu _s}$, then the magnitude of negative lift ._. acting downwards on the car is: (Assume forces on the four types are identical and g = acceleration due to gravity)

A. $m\left( {\dfrac{{{v^2}}}{{{\mu _s}R}} - g} \right)$
B. $m\left( {\dfrac{{{v^2}}}{{{\mu _s}R}} + g} \right)$
C. $m\left( {g - \dfrac{{{v^2}}}{{{\mu _s}R}}} \right)$
D. $ - m\left( {g + \dfrac{{{v^2}}}{{{\mu _s}R}}} \right)$

Answer 1

Hint:Before we proceed with the problem, it is important to know the definitions of static friction, centripetal force and weight. Static friction can be defined as the force that resists the movements of an object along the path. The centrifugal force is the force that is directed radially outward to a circular path. It arises due to the circular motion of the body. Weight is a type of force that is the product of the mass of the body and gravitational acceleration.

Formula used:
From the formula of centrifugal force
$f = \dfrac{{m{v^2}}}{R}$,
Here f is the centrifugal force, m is the mass of the body, v is the velocity of the body and R is the radius of the path.
From the formula of static friction,
$f = {\mu _s}N$
Here f is the frictional force, ${\mu _s}$ is the coefficient of static friction and N is the normal force.
From the formula of weight
$W = mg$
Here m is the mass of the body, g is the gravitational acceleration.

Complete step by step solution:

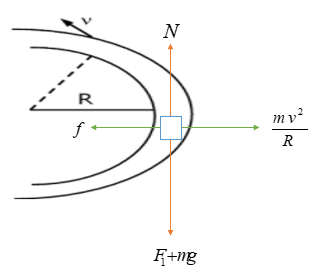
Image: A racing car is moving on a flat track in a circular arc.
The mass of modern grand-prix racing car = m
The radius of the circular arc = R
The speed of the car = v
The coefficient of static friction between the tyres and the track = ${\mu _s}$
The magnitude of negative lift ${F_1}$ acting downwards.
Static friction can be defined as the force that resists the movements of an object along the path. This static frictional force is equal to the centripetal force.
The centrifugal force is the force that is directed radially outward of a circular path. It arises due to the circular motion of the body.
The static friction = The force that balances along the radial direction
$f = \dfrac{{m{v^2}}}{R} \\ $….(1)
The relation between static frictional force and normal force
$f = {\mu _s}N$…..(2)
The normal force is a reaction force. It is an upward force which arises due to the weight of the body.
The total upward force = total downward force
The normal force = The force balancing along the vertical direction
Normal force = ${F_1}$(downward force) + weight of the body
$N = {F_1} + mg$……..(3)
Equating equation (1) and equation (2)
${\mu _s}N = \dfrac{{m{v^2}}}{R} \\ $
Substituting the value of N in the above equation
$\begin{array}{l}{\mu _s}\left( {mg + {F_1}} \right) = \dfrac{{m{v^2}}}{R}\\ \Rightarrow mg + {F_1} = \dfrac{{m{v^2}}}{{R{\mu _s}}}\\ \Rightarrow {F_1} = \dfrac{{m{v^2}}}{{R{\mu _s}}} - mg\\ \therefore {F_1} = m\left( {\dfrac{{{v^2}}}{{R{\mu _s}}} - g} \right)\end{array}$

Hence, the correct option is Option A.

Note:Students usually make mistakes by taking the value of radius including the width of the path. We need to assume the relation of static frictional force, normal force and frictional coefficient relation.