Question

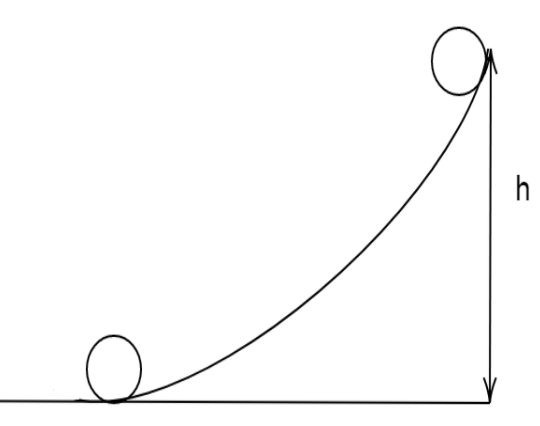
A hollow sphere is set rolling with a speed $V$ on a rough surface, as shown in the figure. Assuming no slipping, find out the height $h$ where it will come to instantaneously rest.

Answer 1

Hint: As the sphere comes to a rest after rolling, we can say that kinetic energy is converted to potential energy. The Kinetic energy initially is due to both rotatory and translatory motion. Thus, using the conversion of energy, we can find the solution.

Complete step by step solution:
We know for rolling bodies, kinetic energy is expressed as the sum of translational kinetic energy and rotational kinetic energy.
So, we can say:
$K.E. = {T_{KE}} + {R_{KE}}$
Where,
${T_{KE}}$ is the translational Kinetic energy
${R_{KE}}$ is the Rotational Kinetic energy
$K.E.$ is initial kinetic energy.
Again, we know that the translational kinetic energy depends on the mass and velocity of the object.
So, ${T_{KE}} = \dfrac{1}{2}m{v^2}$
$m$ is the mass of the object
$v$ is the velocity of the object
Also, the rotational kinetic energy can be written as:
${R_{KE}} = \dfrac{1}{2}I{\omega ^2}$
$I$ is the moment of inertia
$\omega$ is the angular velocity
Hence, we write:
$\Rightarrow K.E. = \dfrac{1}{2}m{V^2} + \dfrac{1}{2}I{\omega ^2}$
We also know,
$V = \omega r$
$V$ is the linear Velocity
$\omega$ is the angular velocity
$r$ is the radius.
We know the moment of inertia for the hollow sphere is $I = \dfrac{2}{3}M{R^2}$
Since both $M$ and $m$ represents the mass of the sphere, we can say:
$M = m$
And both $r$ and $R$ points to the same radius.
Thus, we substitute the value in the equation:
$\Rightarrow K.E. = \dfrac{1}{2}m{V^2} + \dfrac{1}{2}(\dfrac{2}{3}M{R^{2)}}{(\dfrac{V}{r})^2}$
Therefore, in solving this, we get:
$\Rightarrow K.E. = \dfrac{1}{2}m{V^2} + \dfrac{1}{3}m{V^2}$
Thus, we obtain:
$\Rightarrow K.E. = \dfrac{5}{6}m{V^2}$
Now, due to conservation of energy, we consider kinetic energy is converted to potential energy:
$\Rightarrow PE = mgh$
Where,
$PE$ is the potential Energy
$m$ is the mass of the object
$g$ is the acceleration due to gravity
$h$ is the height
Thus, we write:
$\Rightarrow mgh = \dfrac{5}{6}m{V^2}$
On rearranging the equation, we arrive at:
$\Rightarrow h = \dfrac{{5{V^2}}}{{6g}}$

Note: We know, as the sphere rolls initially, we can say that it is in motion. Thus, the energy of a body in motion is referred to as its kinetic energy. Since the body rolls, we consider kinetic energy for rolling bodies, and as the body moves to rest, we consider the potential energy.