Question

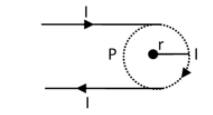
A hairpin-like shape as shown in the figure is made by bending a long current-carrying wire. What is the magnitude of a magnetic field at point P which lies on the centre of the semicircle?

a) \[\dfrac{{{\mu _o}I}}{{4\pi R}}\left( {2 - \pi } \right)\]
b) \[\dfrac{{{\mu _o}I}}{{4\pi R}}\left( {2 + \pi } \right)\]
c) \[\dfrac{{{\mu _o}I}}{{2\pi R}}\left( {2 + \pi } \right)\]
d) \[\dfrac{{{\mu _o}I}}{{2\pi R}}\left( {2 - \pi } \right)\]

Answer 1

Hint: Here, we will need to consider three cases to find total magnetic induction at point P which is at distance r from the line and semicircle.

Complete answer:
The magnetic influence on moving electric charges, electric currents, and magnetic materials is described by a magnetic field, which is a vector field. A force perpendicular to the magnetic field and its own velocity acts on a moving charge in a magnetic field.

A second application of the right-hand rule can be used to determine the magnetic field's direction. Your fingers will wrap around the wire in the same way that B does if you hold the wire in your right hand with your thumb pointing along the current.

If you do not recollect the formula, you can derive it using Biot Savarts law, which states that:-
\[dB = \dfrac{{{\mu _O}I\int {\sin \theta dl} }}{{4\pi {r^2}}}\]

By substituting appropriate terms with \[\sin \theta \], and then integrating w.r.t r, one can easily find Magnetic Induction at a point for any mathematically integrable object.

Now,
Magnetic field due to straight wire is, \[\dfrac{{{\mu _o}I}}{{4\pi R}}\]
Magnetic field at centre of semicircle is, \[\dfrac{{{\mu _o}I}}{{4R}}\]
Total Magnetic field at point P(B) = \[\dfrac{{{\mu _o}I}}{{4\pi R}}\]+\[\dfrac{{{\mu _o}I}}{{4\pi R}}\]+\[\dfrac{{{\mu _o}I}}{{4R}}\]
B=\[\dfrac{{{\mu _o}I}}{{4\pi R}}\]+\[\dfrac{{{\mu _o}I}}{{4\pi R}}\]+\[\dfrac{{{\mu _o}I\pi }}{{4\pi R}}\]
B = \[\dfrac{{{\mu _o}I}}{{4\pi R}}(2 + \pi )\]

Hence, The answer is b) \[\dfrac{{{\mu _o}I}}{{4\pi R}}\left( {2 + \pi } \right)\]

Note: To be able to solve this type of sum easily, one should be thorough with all the formulas related to Magnetic field. Some of the important ones are Magnetic field due to infinite wire, Magnetic field due to finite wire, Magnetic field at the centre of circle.