JEE Advanced 2025 Atomic Structure and Chemical Bonding Revision Notes

Atom: Fundamental building block of matter.

Subatomic Particles: Atoms consist of smaller particles like electrons, protons, neutron, neutrino, and antineutrino, positron, ant positron, peons and mesons etc.

Fundamental Particle of Atoms: Electrons, protons neutrons

Specific Charge: The charge to mass ratio is known as specific charge $\left( \dfrac{e}{m} \right)$;$\dfrac{e}{m}=1.7588\times {{10}^{11}}Ck{{g}^{-1}}(\text{or})1.7588\times {{10}^{8}}C{{g}^{-1}}$.

The mass of moving electron may be calculated by applying the formula $m=\dfrac{{{m}_{0}}}{\sqrt{1-{{\left( \dfrac{v}{c} \right)}^{2}}}}$,

${{m}_{0}}$ = rest mass of electron; v = velocity of electron; c = velocity of light

• If v = c, the mass of the moving electron becomes infinity.

• The value  $\left( \dfrac{e}{m} \right)$ of cathode ray is independent of the nature of metal used as cathode and the gas used in the discharged tube.

$\left( \dfrac{e}{m} \right)$value of ions w.r.t H-atom: $\dfrac{\text{magnitude of charge(relative charge)}}{\text{mass number(relative mass)}}$

Charge of Electron:

The charge of electrons is the smallest known electrical charge, it is taken as unit negative charge.

• Millikan determined the charge of electrons by oil drop experiment.

• Charge on the oil drop was always an integral multiple of $1.6022\times {{10}^{-19}}C$.

Mass of Electron:

Neutron:

• Neutrons discovered by James Chadwick.

• When beryllium boron nuclei are bombarded by alpha particles, neutrons are formed.

• They have no charge but mass is almost equal to protons.

$Be_{4(Beryllium)}^{9}+H_{2(\alpha -particle)}^{4}\to C_{6(carbon)}^{12}+n{{_{0}^{1}}_{\left( neutron \right)}}$

• Mas concentrated at the centre indicates the nucleus. 

• The radius of the atom is very small and in the order of 10^-10 m, where for nucleus is 10^-15

Distance of Closest Approach:

The distance up to which alpha particles come closer to the nucleus is called distance of closest approach.

• Its value can be determined by conservation of energy principle $\therefore \dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{(Ze)(2e)}{{{r}_{0}}}$.

• $\dfrac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}$.

Atomic Number:

The number of protons present inside the nucleus of an atom of an element, it is denoted by (Z).

• For Cation:

Number of protons = Z

Number of electrons = Z - number of electrons lost

• For anion:

Number of protons = Z

Number of electrons = Z + number of electrons lost

Mass Number:

The sum of protons and neutrons in an atom, denoted by (A).

A = n + z (number of neutrons + number of protons)

Number of neutrons: A – Z

Mass number is always a whole number 

Isotopes:

The atoms of the same elements having the same atomic number but different mass numbers are called isotopes.

Average atomic mass $=\dfrac{\sum{{{A}_{i}}{{x}_{i}}}}{\sum{{{x}_{i}}}}$

A = atomic mass of isotopes

X = percentage abundance of isotope

Isobars:

The atoms with a different element having same mass number but different atomic number 

Shows similar physical properties but different chemical properties

Ex: $C_{6}^{14},N_{7}^{14}$ 

Isotones:

The nuclides with the different elements with different atomic number and mass number but having the same number of neutrons.

(A-Z) : Shows different physical and chemical properties

Ex: $Si_{14}^{30},P_{15}^{31},S_{16}^{32}$

Iso Diaphers:

The nuclides having the same isotopic number (A-2Z) are called iso diaphers. They possess the same difference of neutrons and protons(n-p).

E.g.: $_{9}^{19}F, _{11}^{23}Na$

Isosteres:

The molecules with the same atomicity and the same number of electrons are called isosteres’.

Atomicity = total number of atoms in molecules

Iso-Electronic Species: 

The molecules or ions with same number of electrons are called isoelectronic species

Ex: ${{N}^{-3}},{{O}^{-2}},{{F}^{-}},Ne,N{{a}^{+}}$.

Nature of Light:

It can be explained by two theories:

1. Wave theory of light

2. Corpuscular theory of light

Wave Theory:

• When an electrically charged particle moves under exacerbations alternating electric and magnetic fields are produced and transmitted.

• These are transmitted in the form of waves and are associated with electrical and magnitude fields produced and transmitted.

• Both electric and magnetic fields are mutually perpendicular and perpendicular to direction of the propagation.

• These electromagnetic waves do not require any medium and can travel in vacuum.

• Intensity α maximum magnetic field × maximum electric field $I\,\text{ }\!\!\alpha\!\!\text{  }{{E}_{0}}{{B}_{0}}$
  
  

Wave Theory

Characteristic Properties of a Wave

Wave length: The distance between two similar points in wave is known as wavelength 

Frequency: The number of waves that pass-through a given point in one second is called frequency.

Frequency(v) and wavelength $(\lambda )$ are related as $v=\dfrac{c}{\lambda }$ velocity of light = 3×10⁸ m/sec

Wave number: Relation between $v$ and $\bar{v}$ is $v=c\overline{v}$

Amplitude (a): The height of the crest or depth of the trough of a wave.  

Unit: m, cm, pm.

Velocity: The distance travelled by a wave in one second.

Planck’s Quantum Theory 

The energy of the quantum of radiation is directly proportional to the frequency of the radiation.

$E\,\text{ }\!\!\alpha\!\!\text{ }\,V$;$E=h\upsilon ;E=\dfrac{hc}{\lambda }=hc\overline{v}$

E = energy of radiation; h = Planck’s constant

$=6.625\times {{10}^{-27}}erg-\sec$

$=6.625\times {{10}^{-34}}Joule-\sec$

$=3.99\times {{10}^{-13}}kJ-\sec /mole$

Compton Effect: The increase in wavelength or decrease in energy of the x-ray after scattering from an object.

Photoelectric Effect: The phenomenon of ejection of electrons from the surface of metal when light of suitable frequency strikes.

In photoelectric effect the number of photons falling on unit area in unit time $I=\dfrac{\text{no}\text{. of photons}}{A\times t}$.

Spectrum and Atomic Model

The image is recorded when radiant energy is passed through a prism or granting.

• The splitting of white light into seven colours is known as dispersion, the device used to record the spectrum is called a spectrograph or spectrometer.

• Spectrum is broadly divided into two types

Absorption Spectrum: It is the spectrum produced by transmitted lighter after absorption of radiation.

Emission spectrum: Produced by emission of radiation.

• Emission spectrum can be further classified into line and band spectrum

Hydrogen Emission Spectrum:

By applying potential difference in a discharge tube containing hydrogen gas a bright light is obtained.

It Contains a Series of Group of Lines

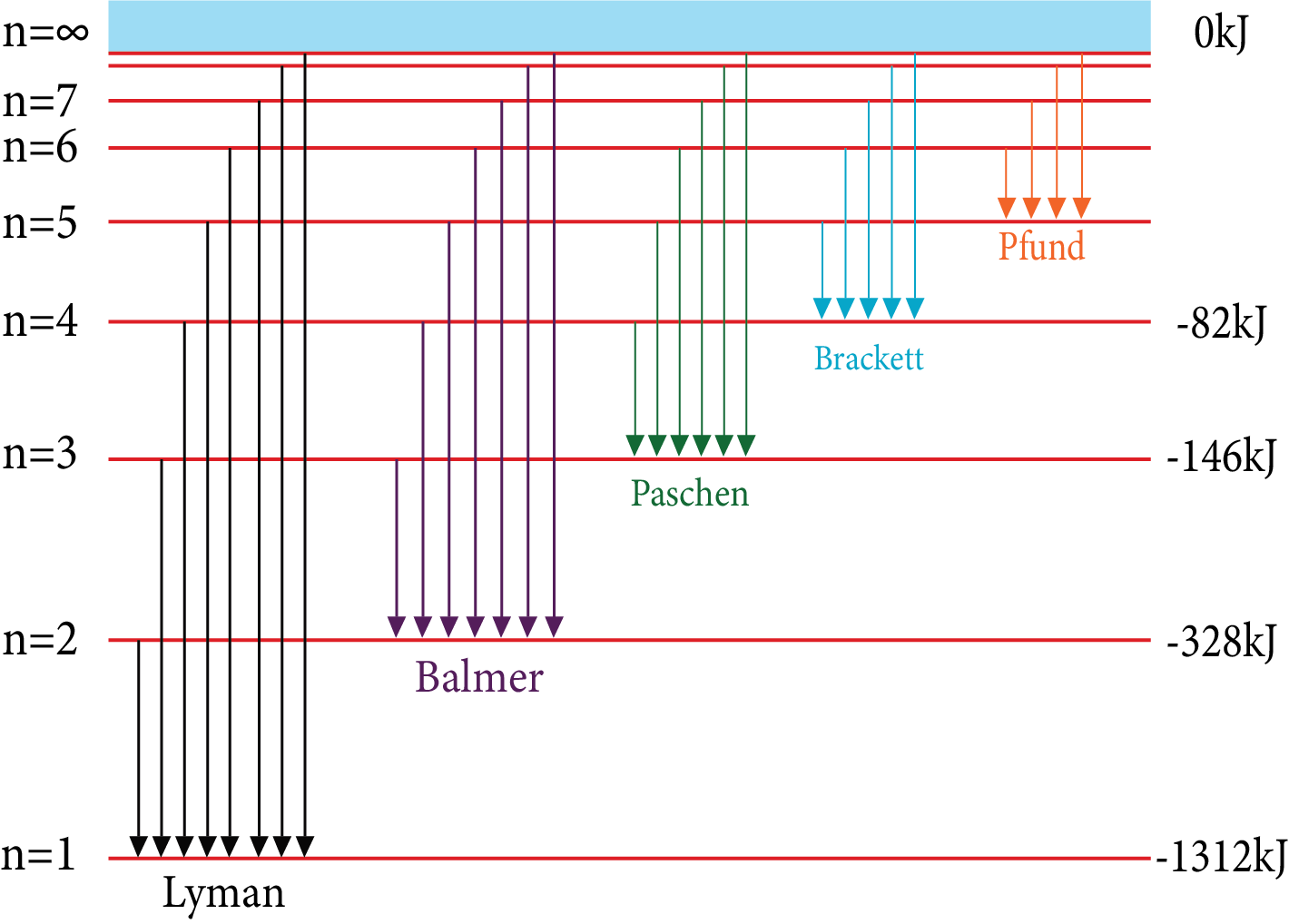
Hydrogen Emission Spectrum

• The wavelength or wave number of all the lines in all the series can be calculated by using Rydberg’s equation

$\overline{v}=\dfrac{1}{\lambda }={{R}_{H}}\times {{Z}^{2}}\left[ \dfrac{1}{n_{1}^{2}}-\dfrac{1}{n_{2}^{2}} \right]$;
R_H= Rydberg’s constant for H-atom=109677 cm^-1;
n₁=Lower energy level; n₂= Higher energy.

• Maximum number of spectral lines produced when an electron jumps from n₂ to n₁ state for a simple atom $=\dfrac{n(n+1)}{2}$, where n= n₂ - n₁

$=\sum{({{n}_{2}}-{{n}_{1}})}$

• Number of spectrum line in a series= n₂ - n₁

Expression for Atomic Radius:

• The centripetal force of attraction $=\dfrac{-Z{{e}^{2}}}{{{r}^{2}}}$

• The centrifugal force$\dfrac{-m{{v}^{2}}}{r}$

• Expression for radius $r=\dfrac{{{n}^{2}}{{h}^{2}}}{4{{\pi }^{2}}mZ{{e}^{2}}}$

• Radius $r=\dfrac{0.529\times {{n}^{2}}}{Z}A{}^\circ $

For H-atom, Z=1, hence r=0.529×n²A⁰

$r=0.529\times {{n}^{2}}\times {{10}^{-8}}cm$

$r=52.9\times {{n}^{2}}pm$

Expression for Energy:

• Kinetic energy $=\dfrac{1}{2}m{{v}^{2}}=\dfrac{Z{{e}^{2}}}{2r}$

• Potential energy $=\dfrac{-Z{{e}^{2}}}{r}$

• Total energy $=E=KE+PE==\dfrac{Z{{e}^{2}}}{2r}-\dfrac{Z{{e}^{2}}}{r}=\dfrac{-Z{{e}^{2}}}{2r}$

Expression for energy of Bohr’s orbit m( by substituting radius of orbit in the above equation)

$E=\dfrac{-2{{\pi }^{2}}m{{Z}^{2}}{{e}^{4}}}{{{n}^{2}}{{h}^{2}}}$.

Rydberg’s constant: $R=\dfrac{2{{\pi }^{2}}m{{Z}^{2}}{{e}^{4}}}{{{h}^{3}}c}=109677\times {{Z}^{2}}c{{m}^{-1}}$

Velocity of electron: $v=\dfrac{2\pi Z{{e}^{2}}}{nh}=\dfrac{2.188\times {{10}^{8}}}{n}cm/\sec $

Number of Revolutions: 

Orbital frequency by an electron in a shell $=\dfrac{\text{velocity}}{\text{circumference}}=\dfrac{v}{2\pi r}=6.66\times {{10}^{15}}\times \dfrac{{{z}^{2}}}{{{n}^{3}}}$

Time period of revolution: of electron in nth orbit

${{T}_{n}}=\dfrac{2\pi r}{{{v}_{n}}}=1.5\times {{10}^{-16}}\times \dfrac{{{n}^{2}}}{{{z}^{2}}}\sec $

Ionisation Potential:

• For hydrogen atom, ionization potential$=\dfrac{{{E}_{1}}}{{{n}^{2}}}$.

• For H-like species, ionisation potential$=\dfrac{{{E}_{1}}\times {{Z}^{2}}}{{{n}^{2}}}$.

• Ionisation potential$=13.6\left[ \dfrac{{{Z}^{2}}}{{{n}^{2}}} \right]eV$.

De-Broglie’s Wave Theory:

According to de- Broglie theory all moving particles have wave properties. Wave properties are important only for particles of small mass and high velocity.

If the velocity of micro particle is v the de- Broglie equation is $\lambda =\dfrac{h}{mv}=\dfrac{h}{p}$.

Schrodinger’s wave equation: $=\left[ \dfrac{{{\partial }^{2}}}{\partial {{x}^{2}}}+\dfrac{{{\partial }^{2}}}{\partial {{y}^{2}}}+\dfrac{{{\partial }^{2}}}{\partial {{z}^{2}}} \right]\psi +\dfrac{8{{\pi }^{2}}m}{{{h}^{2}}}\left( E-V \right)\psi =0$.

Where, $\psi $=Wave function (amplitude of the wave)

m -= mass of electron

h = Planck’s constant

E = Total energy of the electron

V= Potential energy of electron 

Quantum Numbers:

For explanation of electron in atom we require four quantum numbers.

1. Principle Quantum number

• Proposed by Niels Bohr

• Value of n= 1,2,3, or K,L,M,N…

• Indicates the size increase and orbital energy increment

• Maximum number of of electrons in an orbit $=2{{n}^{2}}$

• Total number of orbits = n²

• Angular momentum of an electron in an orbit =$n\dfrac{h}{2\pi }$
  
  

2. Magnetic Quantum Number

• Proposed by Lande

• The value of ml depends on l

• Value ranges from= +l….0….-1

• The number of orbitals in main energy level = n²

• The number of orbitals in subshell = 2l+1

• Maximum number of electrons in a subshell = 2(2l+1)
  
  

3. Spin Quantum number

• Proposed by goldsmith and uhlenbeck

• Value of ms is $+\dfrac{1}{2}$and $-\dfrac{1}{2}$

• Total spin, S=$\pm \dfrac{n}{2}$

• Spin angular momentum of the electron $=\dfrac{h}{2\pi }\sqrt{S(S+1)}$

• Spin multicity = 2s + 1
  
  

4. Azimuthal Quantum Number

• Proposed by Sommerfeld

• L depends on n

• The energies are in the order of s<p<d<f

• Angular momentum of the electron in an orbital $=\dfrac{h}{2\pi }\sqrt{l(l+1)}=h\sqrt{l(l+1)}$

Orbital:

The space around nucleus, where the probability of finding electrons $\left( {{\psi }^{2}} \right)$ is maximum, the maximum probability of finding an electron in an orbit is 95%.

Shapes of Atomic Orbit:

S-orbital:

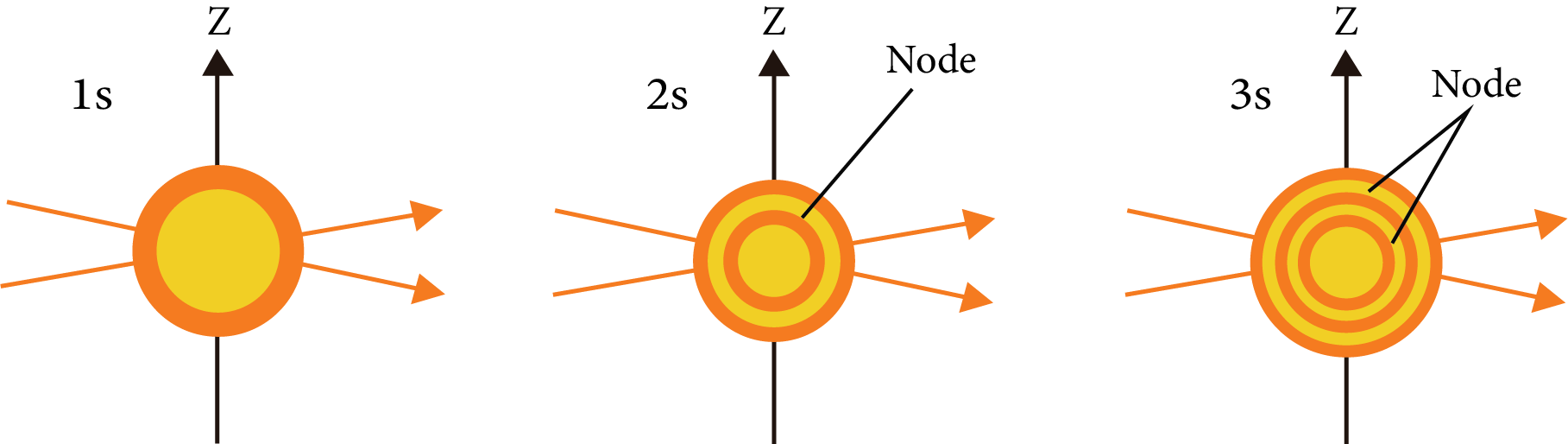
S-orbital

P-orbital:

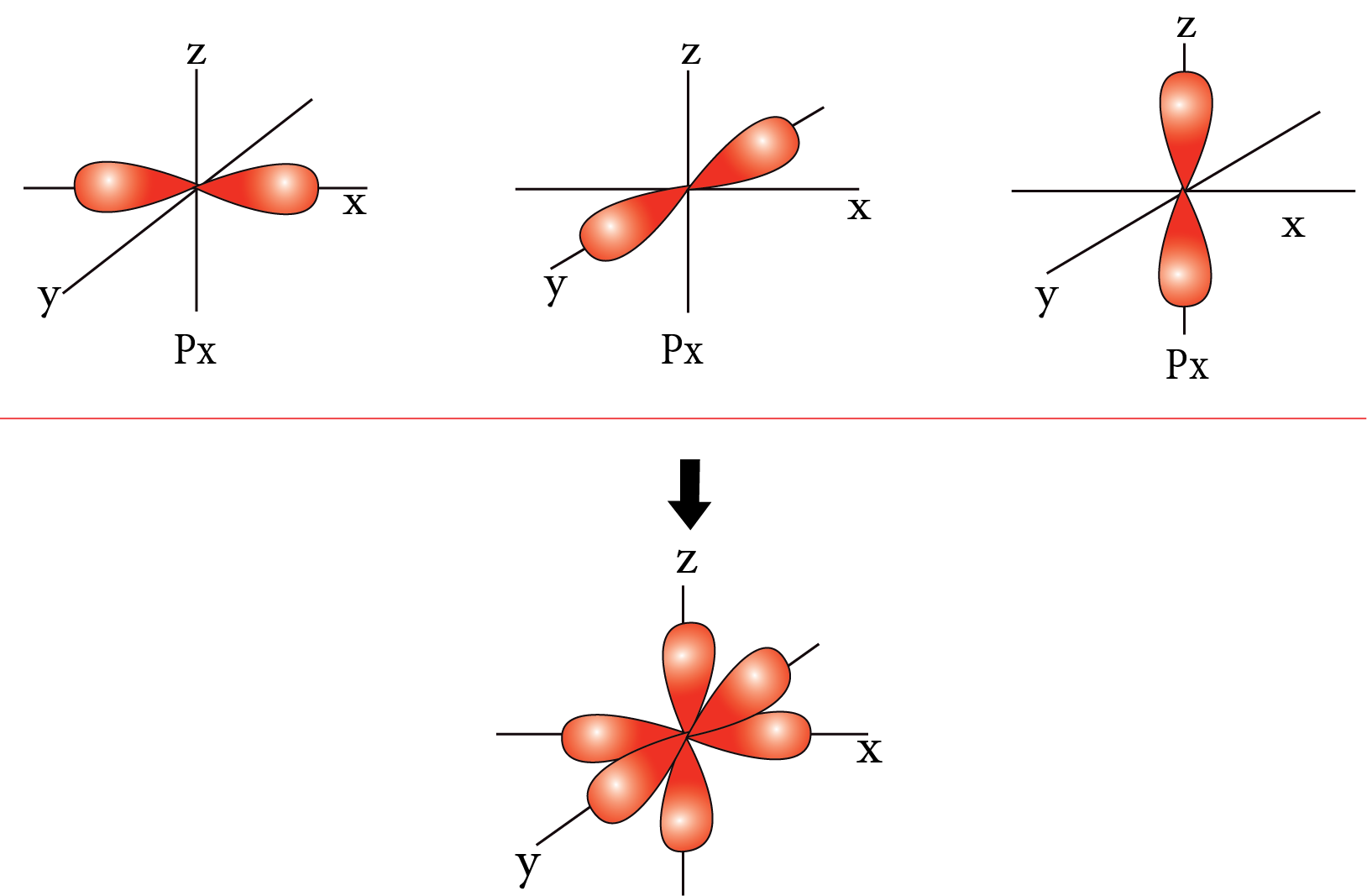
P-orbital

D-orbital:

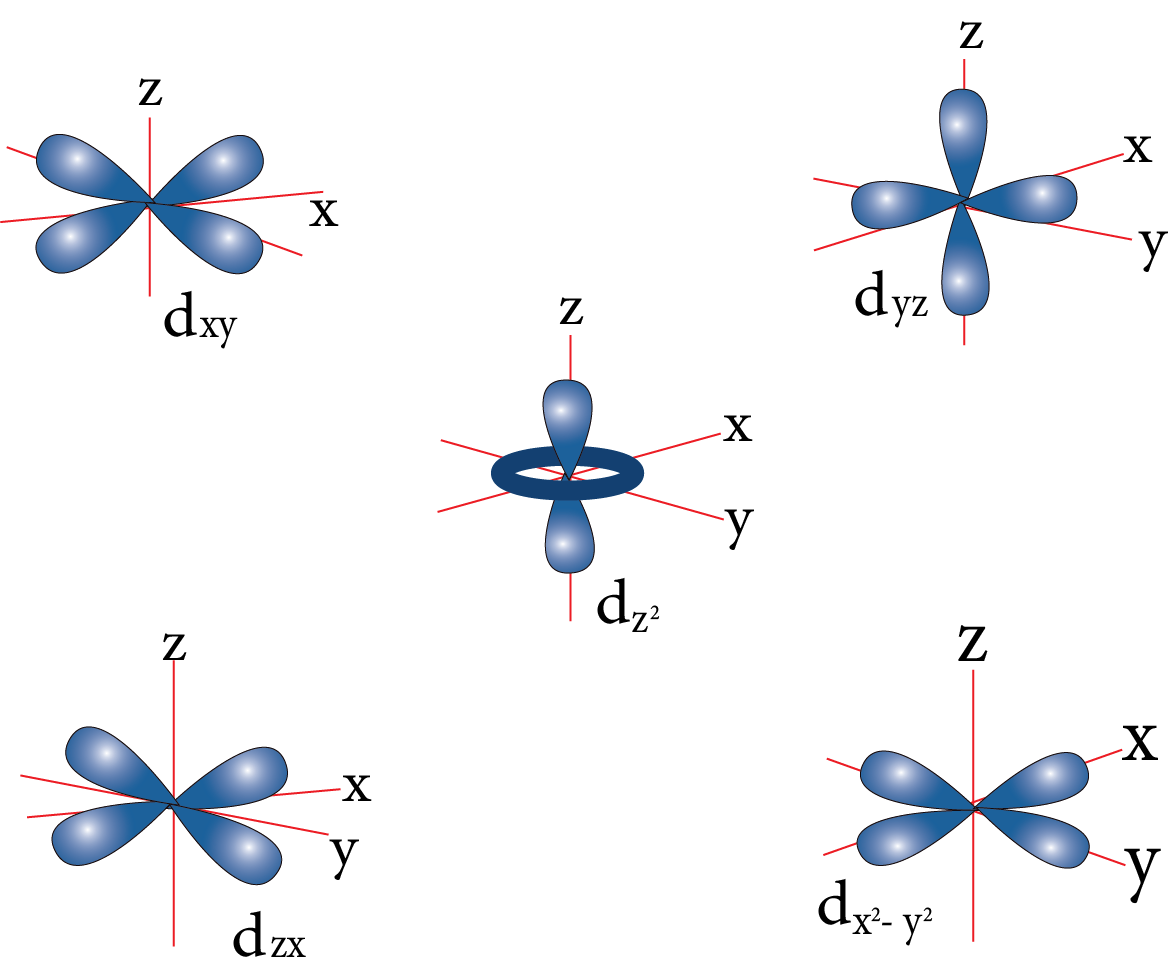
D-orbital

F orbital:

F-orbital

Nodal plane: The plane in which the probability of finding electron density is zero.

Number of the nodal plane (or) angular nodes for an orbital = l

The distribution of electrons into orbitals of an atom is called electronic configuration

Aufbau Principle:

In the ground state of the atom, the orbitals are filled in the order of their increasing energies.

Pauli’s Exclusion Principle:

Gives restrictions in filling of various orbitals with electrons.

It states that no two electrons in an atom can have same set of all four quantum numbers.

Hund’s Rule:

It deals with filling up of degenerate orbit with electrons (degenerate = orbitals of equal energies).

Importance of Atomic Structure and Chemical Bonding

The elements and compounds exist in different forms and structures. The atomic structure of the constituent atoms determines the type of chemical bonding between them. It also explains how the compounds form and what kind of chemical bonds are produced due to sharing or transfer of electrons.

The construction of an atomic structure is the basis of this subject. The electronic configuration of an atom depends on the number of electrons. The electrons present outside the nucleus determine how an atom will behave physically and chemically.

With the aid of Chemical Bonding JEE notes, you will understand the basic and advanced scientific principles related to ionic, covalent and metallic bonds. Find out the difference between the atoms of different elements in a periodic table. 

This chapter can be considered the base of inorganic and organic chemistry. Hence, it is quite crucial for your JEE Advanced chemistry preparation. The easier format of the revision notes prepared by the subject experts will guide you to understand and remember the concepts taught in this chapter. Focus on how the concepts have been simplified and explained in these notes to strengthen your conceptual foundation. 

Benefits of Chemical Bonding JEE Notes

• These notes have been curated by the top subject experts at Vedantu as per the latest JEE syllabus. 

• All concepts are explained with illustrations making them easier to understand for students. It will help you to understand the scientific theories and explanations covered in this chapter.

• You will also be able to solve problems by referring to the chemical bonding notes IIT JEE PDF. Use these notes to revise this chapter and recall what you have studied here in no time. 

• Download and refer to the PDF anywhere anytime for absolutely free from Vedantu. 

Download Chemical Bonding Revision Notes PDF For JEE Advanced

The free PDF version of the Chemical Bonding revision notes will help complete the studying of this chapter. Find out how the electronic configuration of an atom influences the formation of chemical bonds resulting in different types of compounds. You can use these notes to learn about chemical bonds and the atomic structure of different elements to strengthen your concepts in chemistry. 

Important Related Links for JEE Main and JEE Advanced