Courses

Courses for Kids

Free study material

Store

Talk to our experts

1800-120-456-456

Electricity and Magnetism - Physics JEE Advanced

JEE Advanced

Physics

Electricity And Magnetism

Last updated date: 25th Apr 2024

•

Total views: 62.4k

•

Views today: 1.62k

Concepts of Current Electricity and Magnetism for JEE Advanced Physics

When it comes to JEE Advanced exams, there is no chapter which can be ignored. Just like most of the chapters electricity and magnetism plays a vital role in scoring good grades and ranking. Because of its vast syllabus and concepts, electricity and magnetism are considered one of the most important chapters for JEE advanced exams.

The electricity and magnetism chapter consists of many sub-topics that are considered to be very basic and important. The first concept that we get to see in electricity and magnetism notes is electrostatics. The unit electrostatics and charges is a fundamental part of current electricity and magnetism. In this chapter, we study the link between electricity and magnetism.

The key concepts of the electricity and magnetism chapter are electrostatics, current electricity and the laws related to it, capacitance, magnetostatics, electromagnetic induction, etc.

In this article, we will discuss the electricity and magnetism chapter and the important concepts of the chapter for JEE exam. Let’s start!

JEE Advanced Physics Chapters 2025

JEE Advanced Physics Chapters
1	General Physics	5	Electromagnetic Waves
2	Mechanics	6	Optics
3	Thermal Physics	7	Modern Physics
4	Electricity and Magnestism

Important Topics of Electricity and Magnetism Chapter

Coulomb's law
Gauss law
Electric potential and capacitance
Ohm’s law
Kirchoff’s current and voltage law
Wheatstone Networks
Biot-Savart’s law
Ampere’s law
Electromagnetic induction
Faraday’s law and Lenz law
LC, RC and LCR circuits
LCR series and parallel connections

Electricity and Magnetism Important Concept of JEE Advanced

Name of Concept	Key Point
Coulomb's law	This law of electrostatics is a fundamental statement that rules electrostatics. This law states that the force of attraction or repulsion between two charges will be directly proportional to the product of two charges and inversely proportional to the square of the distance between them.
Electric dipole	An electric dipole is a couple of opposite charges q and –q separated by a finite distance d.
Gauss law	The gauss law introduces us to the concept of electric flux $\phi$. Gauss law states that the total of the electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity.
Ohm’s law	Ohm’s law is a basic principle used in study of electrodynamics or current electricity. The law gives a relationship between the voltage, current and resistance offered. Mathematically stated as: $V \propto I$ i.e., The voltage applied in the circuit will be directly proportional to the current flowing in the circuit.
Kirchhoff's Current Law and Voltage Law	Current law: The total current entering the node must be equal to the total current leaving the node. I.e., Iin=Iout Voltage law: In any closed circuit, the total voltage will be equal to the sum of the voltage drop within the circuit. I.e., V=V1+V2+...
Fleming’s Right Rule	If we arrange our thumb, forefinger and middle finger of the right-hand perpendicular to each other, then The thumb points towards the direction of the motion of conductor relative to the magnetic field. The middle finger points towards the direction of the induced current. The forefinger points towards the direction of the magnetic field.
Fleming’s Left Rule	If we arrange our thumb, forefinger and middle finger of the left-hand perpendicular to each other, then The thumb points towards the direction of the force experienced by the conductor. the forefinger points towards the direction of the magnetic field. The middle finger points towards the direction of the electric current.
Biot Savart’s Law	It states that: “the magnetic field due to a tiny current element at any point is proportional to the length of the current element, the current, the sine of the angle between the current direction and the line joining the current element and the point, and inversely proportional to the square of the distance of that point. The direction of the magnetic field is in the direction of dl cross r.”
Ampere’s law	Statement: “The magnetic field created by an electric current is proportional to the size of that electric current with a constant of proportionality equal to the permeability of free space.”
Magnetic force	Magnetic force is given by $\vec F= q\left(\vec v\times \vec B\right)$
Hysteresis Loop	If we take a ferromagnetic material in completely demagnetized state and make it to undergo through a cycle of magnetization in which H is increased from zero to a maximum value Hmax, then decreases to zero, then reversed and again taken to –Hmax, and finally brought back to zero.
Magnetic substances	Pramagnetic: The substances which when placed in a magnetic field acquires a feeble magnetization in the same sense as the applied field Diamagnetic: The magnetic substances which can be easily magnetised are known as diamagnetic substances.
Electromagnetic Induction	Electromagnetic Induction is the phenomenon in physics where a changing magnetic field induces an electromotive force (EMF) or electric current in a conductor. This principle, elucidated by Faraday's law and Lenz's law, is pivotal in various technological applications and plays a critical role in understanding the behavior of electrical circuits and devices. The fundamental concepts of electromagnetic induction, including the relationship between magnetic flux, EMF, and the rate of change of magnetic flux, as well as the direction of induced currents. It is essential for solving complex problems in electromagnetism, electromechanical systems, and electrical engineering.
Magnetic Induction	Magnetic induction is the process by which an ordinary piece of iron briefly develops magnetic characteristics due to the presence of another magnet close by.
Magnetic Field Near a Current-Carrying Straight Wire	Understanding the magnetic field produced by a straight current-carrying wire is a key application of Biot-Savart's law. The magnetic field lines form concentric circles around the wire, and the field's strength decreases as you move further away from the wire. The magnitude of the magnetic field at a distance 'r' from the wire can be calculated using the formula: \[ B = \frac{\mu_0 I}{2\pi r} \] Here, 'B' represents the magnetic field, 'I' is the current, and 'r' is the distance from the wire.
Magnetic Field Along the Axis of a Circular Coil	When a current flows through a circular coil, it creates a magnetic field along the axis of the coil. The magnitude of the magnetic field at a point on the axis can be calculated using the following formula: \[ B = \frac{\mu_0 nI R^2}{2(R^2 + z^2)^{\frac{3}{2}}}\] Where: 'B' is the magnetic field strength. 'n' is the number of turns per unit length. 'I' is the current. 'R' is the radius of the coil. 'z' is the distance along the coil's axis.
Magnetic Field Inside a Long Straight Solenoid	A solenoid is a long coil of wire, and inside it, the magnetic field is almost uniform. The formula for the magnetic field inside a long straight solenoid is: \[ B = \mu_0 n I \] Where: 'B' is the magnetic field strength. 'n' is the number of turns per unit length. 'I' is the current.
Force on a Moving Charge and on a Current-Carrying Wire in a Uniform Magnetic Field	When a charged particle moves through a magnetic field, it experiences a magnetic force known as the Lorentz force. The formula for this force on a moving charge 'q' is: Lorentz Force: \[ \vec{F} = q \vec{v} \times \vec{B} \] Force on a Current-Carrying Wire: \[ \vec{F} = I \int \vec{dl} \times \vec{B} \] For a current-carrying wire of length 'l' in a magnetic field, the force can be calculated using:
Magnetic Moment of a Current Loop	The magnetic moment (μ) of a current loop is a measure of its ability to generate a magnetic field. It can be calculated using the formula: μ=I⋅A
Effect of a Uniform Magnetic Field on a Current Loop	When a current loop is placed in a uniform magnetic field, it experiences a torque (τ) that tends to align the loop with the field. The torque can be calculated as: τ=μ⋅B⋅sinθ Where: τ is the torque. μ is the magnetic moment. 'B' is the magnetic field strength. θ is the angle between the magnetic moment and the magnetic field.
Moving Coil Galvanometer, Voltmeter, Ammeter, and Their Conversions	Moving coil galvanometers are devices used for measuring small electric currents. When equipped with suitable scales, they can be used as voltmeters and ammeters. Voltmeters are connected in parallel to the circuit, and ammeters are connected in series. The conversion formulas for these devices are as follows: To convert a galvanometer into a voltmeter: \[ R_g = \frac{V}{I_g} - R \] Where: Rg is the resistance to be added in series with the galvanometer. V is the range of the voltmeter. Ig is the current needed for full-scale deflection. R is the resistance of the galvanometer. To convert a galvanometer into an ammeter: \[ R_g = R \left(\frac{I_a}{I_g} - 1\right) \] Where: Rg is the resistance to be added in parallel with the galvanometer. Ia is the desired full-scale current range of the ammeter. Ig is the current needed for full-scale deflection. R is the resistance of the galvanometer.
Electromagnetic waves	Electric field of electro magnetic waves: E(x,t) = Emaxcos(kx - ωt + φ) Where, φ-The phase difference Magnetic field of electro magnetic waves: B(x,t) = Bmaxcos(kx - ωt + φ) Where, φ-The phase difference

List of Important Formulas for Electricity and Magnetism Chapter

Sl. No.	Name of Concept	Formula
1.	Electrostatic Force	$\vec F=\dfrac {k {q_1}{q_2}}{r^2}$ Where, r- The distance between two charges
2.	Electric Field	$\vec E=\dfrac {F}{q}$ Where, F- The electrostatic force
3.	Gauss law	$\phi=\dfrac {q}{\epsilon_o}$
4.	Electric Potential	$V=\dfrac {kq}{r}$ Where, r- The distance between two charges
5.	Ohm’s Law	$V=IR$ Where, R- The resistance of the resistors
6.	Combination of Resistors	Resistors in Series: ${R_s}={R_1}+{R_2}+....$ Resistors in Paralell: ${R_p}=\dfrac {{R_1}{R_2}}{{R_1}+{R_2}}$
7.	Capacitors and Capacitance	Capacitance of the capacitor: $C=\dfrac {q}{V}$ Combination of capacitors: Series: ${C_s}=\dfrac {{C_1}{C_2}}{{C_1}+{C_2}}$ Parallel: ${C_p}={C_1}+{C_2}+....$
8.	Electric field in parallel plate capacitor	$E=\dfrac {\sigma}{\epsilon_o}=\dfrac {Q}{{\sigma_o}A}$
9.	Dielectric constant of a substance	$k=\dfrac {C}{C_o}$
10.	Energy stored in capacitor	$W=\dfrac {1}{2} QV$
11.	Biot savarts law	$dB=\dfrac {\mu_o}{4\pi} \dfrac {I\times dl\times \sin \theta}{r^2}$
12.	Lorentz Force	$F=q\left [\vec E+ \left (\vec v\times \vec B\right)\right ]$
13.	Amperes law	$\int B.dl={\mu_o}I$
14.	Magnetic dipole	$\vec {P_m}=I \vec A$
15.	Magnetic sucesptility	$\chi =\dfrac {I}{H}$
16.	Tangent law	$B=H \tan \theta$

JEE Advanced Electricity and Magnetism Solved Examples

1. A particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x = 3 to x = 5. The minimum value of v required so that the particle can just enter the region.

Sol:

Given,

The mass of the particle=m

Charge of the particle=q

The particle is moving along positive x axis with constant velocity v directed along the negative z axis. Now, we are asked to determine the minimum value of v, for entering the field B.

In this problem, the magnetic field B is perpendicular to the motion of particle the particle in the given region.

Therefore,

The magnetic force=The centripetal force

$qv B=\dfrac {m{v^2}}{r}$

$v=\dfrac {qBr}{m}$

Here, the region is extended from x=3 to x=5, thus the value of r will be:

r=5-3=2

Thus, we get:

$v=\dfrac {2qB}{m}$

Hence, the minimum value of v, for entering the field B is $\dfrac {2qB}{m}$.

Key Point: In this problem we can note one important formula i.e., the minimum value of v when B is perpendicular to the motion of the particle will be $\dfrac {\left({x_2}-{x_3}\right)qB}{m}$.

2. A small circular loop of conducting wire has radius a and carries current I. It is placed in a uniform magnetic field B perpendicular to its plane such that when rotated slightly about its diameter and released, it starts performing simple harmonic motion of time period T. If the mass of the loop is m then :

$T=\sqrt {\dfrac {2m}{IB}}$
$T=\sqrt {\dfrac {\pi m}{IB}}$
$T=\sqrt {\dfrac {\pi m}{2IB}}$
$T=\sqrt {\dfrac {2\pi m}{IB}}$

Sol:

Given that, we have a loop of mass m and radius a, carrying a current I. The current loop is placed in field perpendicular to the magnetic field B.

Now, let us assume that the loop is slightly rotated by an angle $\theta$, then the torque acting on the loop will be:

$\tau = - MB \sin \theta$

$I\alpha=-MB \theta$ (Because, the angle $\theta$ is very small, thus $\sin \theta=\theta$)

$\dfrac {mr^2}{2}\alpha=- \left(\pi {r^2}I\right)B \theta$

$\alpha=\dfrac {2IB\pi}{m}\theta$.....(1)

We know that,

$\alpha = \omega^2 \theta$....(2)

From (1) and (2), we get:

$\omega^2 =\dfrac {2\pi IB}{m}$

$\omega = \sqrt{\dfrac {2\pi IB}{m}}$

Therefore, time period T of rotation will be:

$T=\dfrac {2\pi}{\omega}=\dfrac {2\pi}{\dfrac {2\pi IB}{m}}$

$T=\sqrt {\dfrac {2\pi m}{IB}}$

Therefore, option D is the right answer.

Key Point: To solve the questions like this we need to learn a few standard values of moment of inertia, to save our calculation time.

Previous Year Questions of Electricity and Magnetism

1. A coil having N turns is wound tightly in the form of a spiral with inner and outer radii 'a' and 'b' respectively. Find the magnetic field at centre, when a current I passes through coil: (JEE 2021)

$\dfrac {{\mu_o}IN}{2\left(b-a\right)} \log_e \left(\dfrac {b}{a}\right)$
$\dfrac {{\mu_o}I}{8}\dfrac {a+b}{a-b}$
$\dfrac {{\mu_o}I}{4\left(a-b\right)} \left[\dfrac {1}{a}-\dfrac {1}{b}\right]$
$\dfrac {{\mu_o}I}{8}\dfrac {a-b}{a+b}$

Sol:

Let us consider a small element dr at a distance r. Then the number of turns in the coil will be:

$dN=\dfrac {N}{b-a} dr$

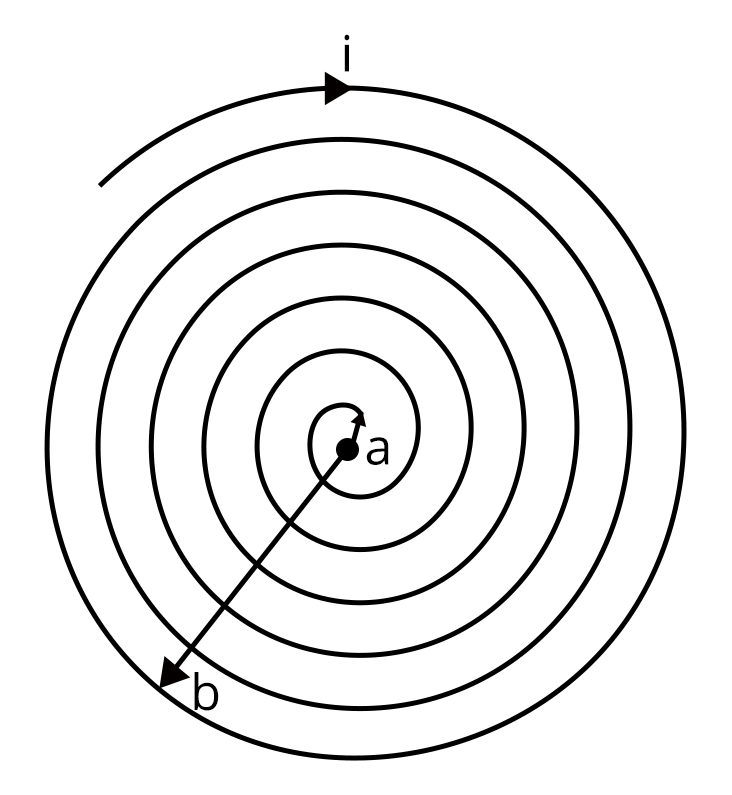
Then the magnetic field due to the element dr at the center of the coil will be:

$dB=\dfrac {{\mu_o}I}{2r} dN$

$dB=\dfrac {{\mu_o}I N}{2 r\left (b-a)\right)}$

$\int_{r=a}^{r=b} dB=\int_{r=a}^{r=b}\dfrac {{\mu_o}I N}{2 r\left (b-a)\right)}$

$B=\dfrac {{\mu_o}I N}{2 \left (b-a)\right)} \log_e \dfrac {b}{a}$

Therefore, option A is the right answer.

Trick: The problem can be easily solved by looking at the the integration part, among all the option, only option A was having logarithmic value.

2. Following plots show magnetization (M) vs magnetizing field (H) and magnetic susceptibility () vs temperature (T) graph : (JEE 2021)

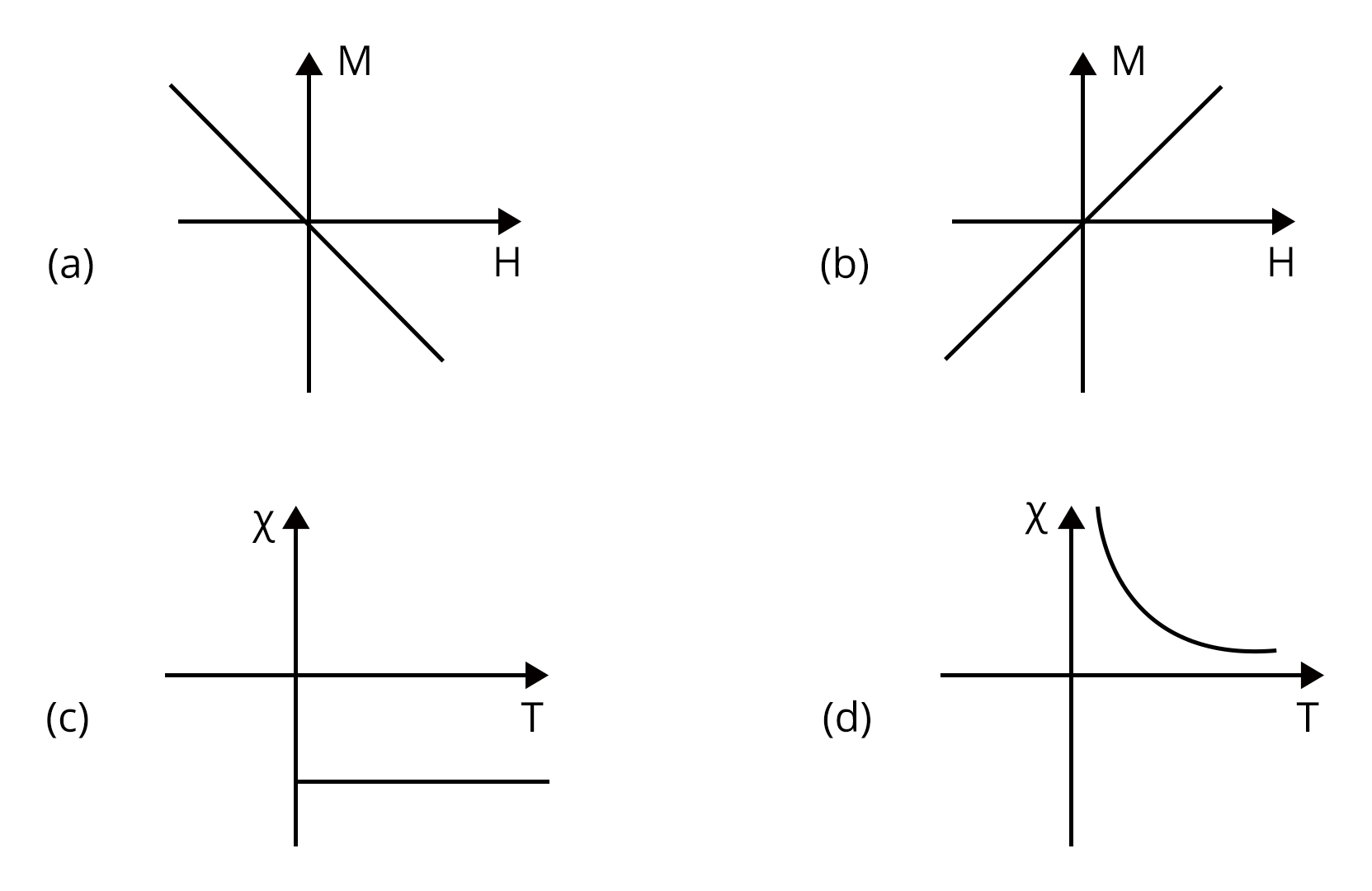
(a), (c)
(a), (d)
(b), (c)
(b), (d)

Which of the following combination will be represented by a diamagnetic material?

Sol:

We know that susceptibility of diamagnetic materials will be negative and independent of temperature. From above graphs, graph (a) and graph (c) represents the diamagnetic material.

Therefore, option a is the right answer.

Trick: From graph eliminate the graphs that are having temperature dependency and porosity susceptibility.

Practice Questions

Electric field of plane electromagnetic wave propagating through a non-magnetic medium is given by E = 20cos(2 1010 t-200x) V/m. The dielectric constant of the medium is equal to : (Take $\mu_r$ = 1) (Ans: 9)
A current of 1.5 A is flowing through a triangle, of side 9 cm each. The magnetic field at the centroid of the triangle is (Assume that the current is flowing in the clockwise direction.) (Ans: $3\times {10^{-5}}$ T, inside the plane of triangle)

JEE Advanced Physics Electricity and Magnetism Study Materials

Here, you'll find a comprehensive collection of study resources for Electricity and Magnetism designed to help you excel in your JEE Advanced preparation. These materials cover various topics, providing you with a range of valuable content to support your studies. Simply click on the links below to access the study materials of Electricity and Magnetism and enhance your preparation for this challenging exam.

JEE Advanced Electricity and Magnetism Study Materials

JEE Advanced Electricity and Magnetism Notes

JEE Advanced Electricity and Magnetism Important Questions

JEE Advanced Electricity and Magnetism Practice Paper

JEE Advanced Physics Study and Practice Materials

Explore an array of resources in the JEE Advanced Physics Study and Practice Materials section. Our practice materials offer a wide variety of questions, comprehensive solutions, and a realistic test experience to elevate your preparation for the JEE Advanced exam. These tools are indispensable for self-assessment, boosting confidence, and refining problem-solving abilities, guaranteeing your readiness for the test. Explore the links below to enrich your Physics preparation.

JEE Advanced Physics Study and Practice Materials

JEE Advanced Physics Previous Year Question Papers

JEE Advanced Physics Formula

JEE Advanced Sample Paper

JEE Advanced Physics Difference Between

Conclusion

The chapter on Electricity and Magnetism stands as a cornerstone in the realm of physics for JEE Advanced aspirants. It delves into the intricate principles governing electric and magnetic fields, laying the foundation for understanding the complexities of electromagnetism. This chapter's profound knowledge is not only crucial for excelling in the exam but also for mastering advanced concepts in physics and engineering. Students who grasp the intricacies of electric and magnetic fields gain the ability to solve intricate problems, analyze real-world applications, and pave the way for innovations in technology. It's a chapter that empowers future scientists and engineers to unlock the mysteries of the physical world.

FAQs on Electricity and Magnetism - Physics JEE Advanced

1. Is electricity and magnetism important for JEE?

In terms of complexity and weightage, 'Electricity and Magnetism' is one of the most important topics in the JEE syllabus. You can be confident of a high overall score if you have a firm grasp on this subject.

2. What is the weightage of electricity and magnetism in JEE Mains?

Due to its vast syllabus electricity and magnetism bagged high weightage in exam. Nearly 5-6 questions have been asked repeatedly which carry about 15-20 marks.

3. Is electricity and magnetism chapters tough?

No, both the chapters are interrelated to each other. Hence if we prepare thoroughly for electricity part, we can easily understand magnetism concepts. So these are not tough chapters.

4. Who unified electricity and magnetism?

Unification of electricity and magnetism credit goes to physicist James Clerk Maxwell.