States of Matter Chapter - Chemistry JEE Main

The bulk properties of matter, i.e the properties of matter that we are familiar with, are represented by the characteristics of chemical systems with which we are familiar. Properties are associated with a large number of items like a collection of atoms, ions, or molecules. A liquid's molecules do not boil, but the bulk does. Water molecules in a collection have wetting properties; Molecules do not wet on their own. Ice is a form of water. It can exist as a solid, as a liquid, or in a gaseous state. Water vapour or steam in a gaseous state. Ice, water, and steam can have very different properties. In the chemical composition of water in all three states, H2O continues to be the same.

JEE Main Chemistry Chapter 2024 

Important Topics of States of Matter Chapter

• Intermolecular Forces

• Thermal energy

• The gaseous state

• The Gas Laws

• Ideal gas equation

• Kinetic energy and molecular speeds

• Kinetic molecular theory of gases

• Behaviour of real gases

• Liquefaction of gases

• Liquid state

1. Intermolecular Forces

The forces of attraction and repulsion between interacting particles are known as intermolecular forces (atoms and molecules). This phrase is used to describe does not take into account the electrostatic forces that exist between the two ions with opposing charges and the forces that hold a molecule's atoms together.

(a) Dispersion Forces or London Forces

• Because their electronic charge cloud is evenly distributed, atoms and nonpolar molecules are electrically symmetrical and have no dipole moment. Even with such atoms and molecules, however, a dipole can form for a brief period of time. 

• The interaction energy is inversely proportional to the sixth power of the distance between two interacting particles, and these forces are always attractive.

(b) Dipole-Dipole Forces

• Between molecules with permanent dipoles, dipole-dipole forces act. The dipoles' ends have "partial charges," which are represented by the Greek character delta .

• Partial charges are always less than the unit electronic charge. The polar molecules interact with their neighbours.

(c) Dipole–Induced Dipole Forces

• This form of attraction exists between polar molecules that have a persistent dipole and molecules that do not have a permanent dipole.

• By deforming the electronic cloud of the electrically neutral molecule, the permanent dipole of the polar molecule produces a dipole on the electrically neutral molecule.

(d) Hydrogen Bond

• This bond is found in compounds that include extremely polar N–H, O–H, or H–F bonds. Although hydrogen bonding is thought to be limited to the elements N, O, and F, species like Cl can also participate. 

• The energy of a hydrogen bond can range from 10 to 100 kJ mol–1. Because hydrogen bonds have such a large quantity of energy, they are a potent factor in influencing the structure and characteristics of many substances, such as proteins and nucleic acids.

• The coulombic interaction between the lone-pair electrons of one molecule's electronegative atom and the hydrogen atom of another molecule determines the strength of the hydrogen bond.

2. Thermal Energy

• Thermal energy is a body's energy derived from the motion of its atoms or molecules. It is directly proportional to the substance's temperature. It is the measure of average kinetic energy of matter particles and is consequently responsible for particle movement. Thermal motion is the name given to this type of particle movement.

3. Intermolecular Forces vs Thermal Interactions

• When molecular interactions are weak, molecules do not stick together to form a liquid or solid until the temperature is lowered to minimise thermal energy. Although molecules get very close to one another and intermolecular tensions are at their highest, -gases do not liquefy solely due to compression.

• When the thermal energy of molecules is reduced by lowering the temperature, the gases become easier to liquefy.

4. The Gaseous State 

We spend our entire lives immersed in the ocean of air, which is made up of a variety of gases. We spend our lives in the troposphere, the lowermost layer of the atmosphere that is held to the earth's surface by gravitational force.

The physical properties that define the gaseous state are as follows.

• Gases can be compressed quite easily.

• Gases apply pressure in all directions equally.

• The density of gases is substantially lower than that of solids and liquids.

• Gases do not have a definite volume or shape. 

• Gases mix uniformly and fully in all amounts without any mechanical assistance, assuming the container's capacity and shape.

5. The Gas Laws

(a) Boyle’s Law (Pressure-Volume Relationship)

Robert Boyle came to the conclusion that the pressure of a fixed amount (i.e., number of moles n) of gas varies inversely with its volume at constant temperature based on his experiments. Boyle's law is the name for this. It can be written as -

P1/V1=P2/V2 at the constant temperature.

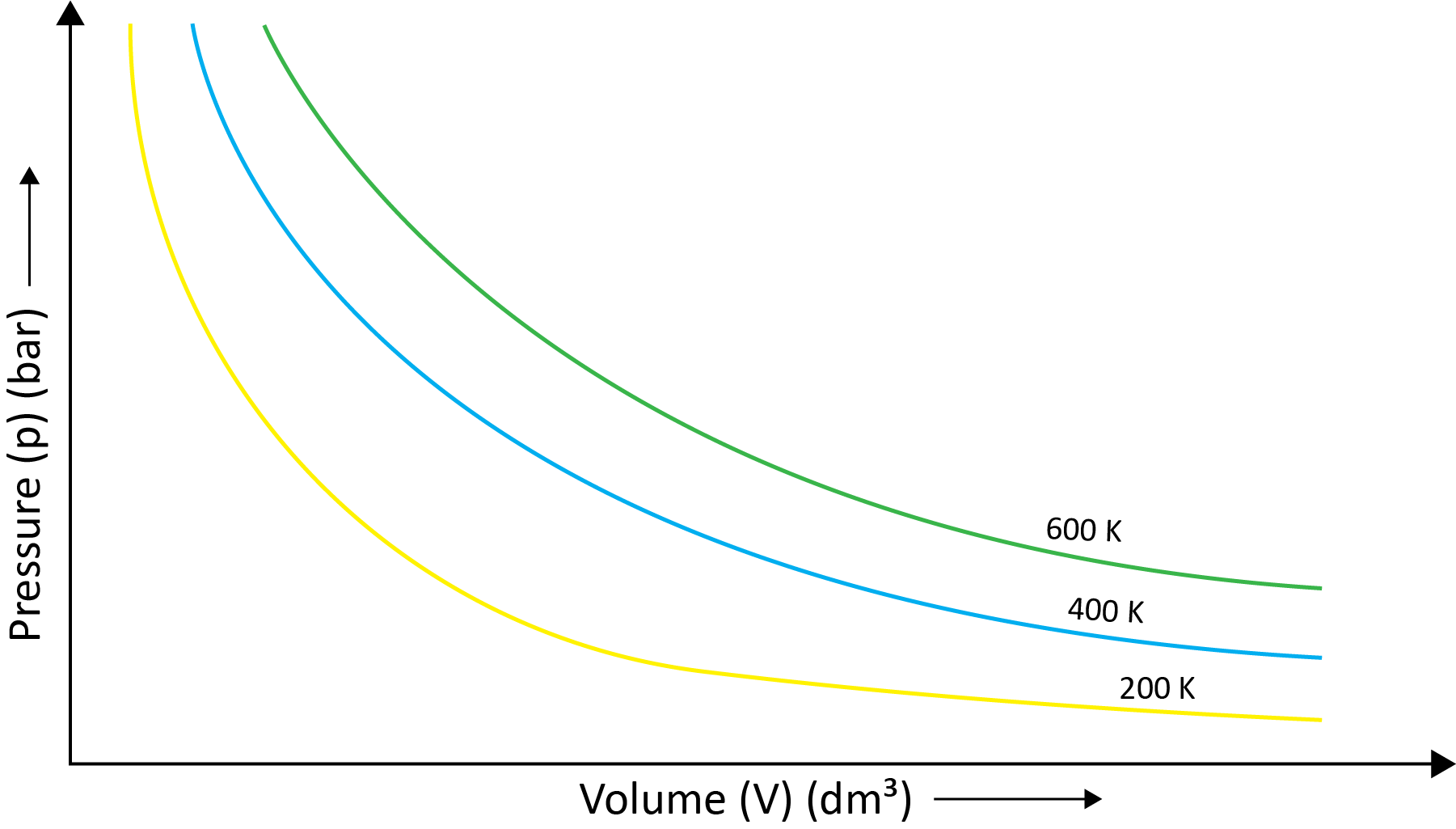
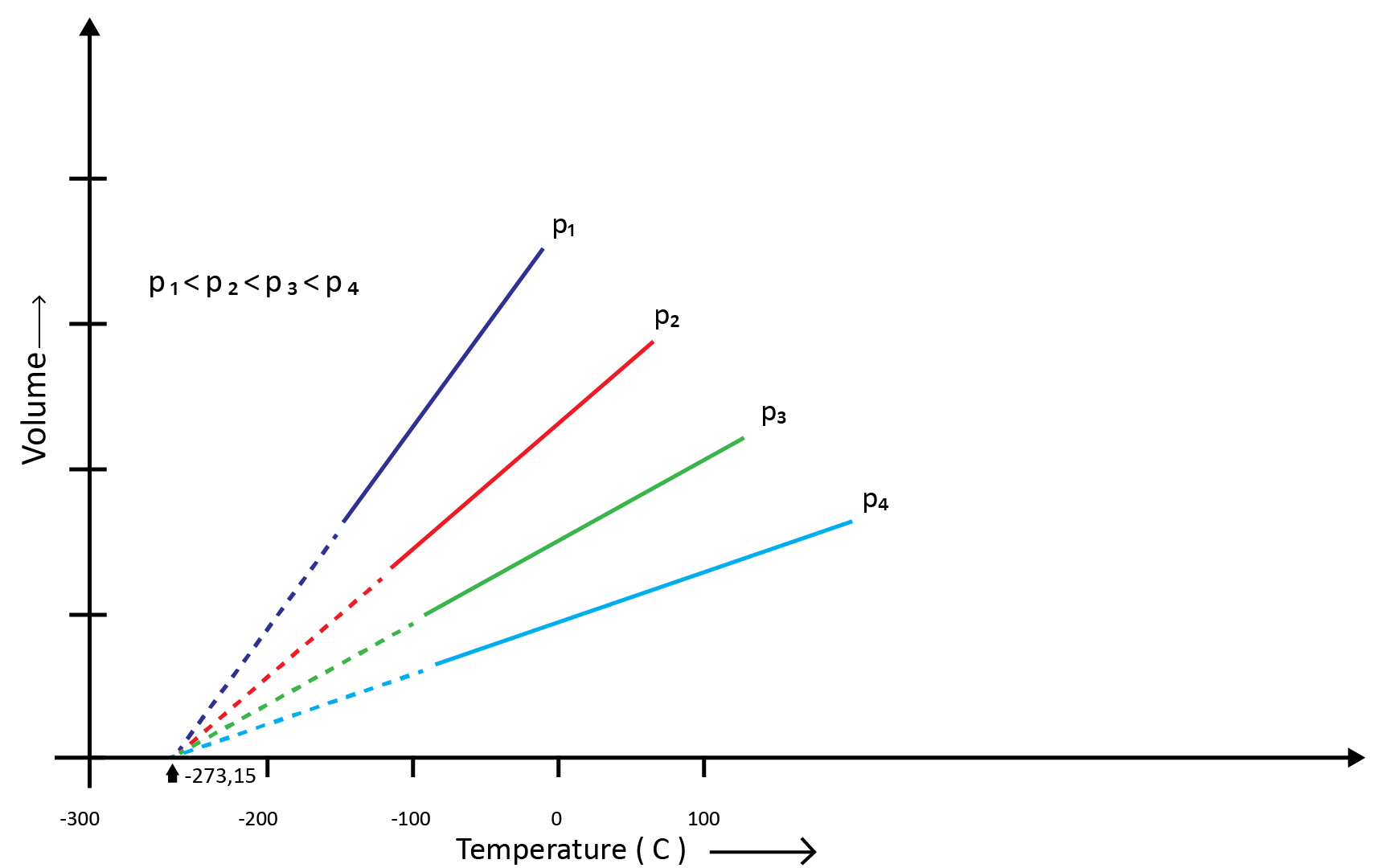
(b) Charles’ Law (Temperature - Volume Relationship)

Charles and Gay Lussac individually conducted various gas experiments in order to advance hot air balloon technology. Their research revealed that the volume of a gas increases with increasing temperature and decreases with cooling for a fixed mass of a gas at constant pressure. The mathematical expression can be given as at the constant volume and pressure-

V1/T1=V2/T2  

(c) Gay Lussac’s Law (Pressure-Temperature Relationship)

Joseph Gay Lussac established the mathematical link between pressure and temperature, which is known as Gay Lussac's law. It claims that the pressure of a fixed amount of gas varies directly with the temperature at constant volume. Mathematically,

P1/T1=P2/T2 

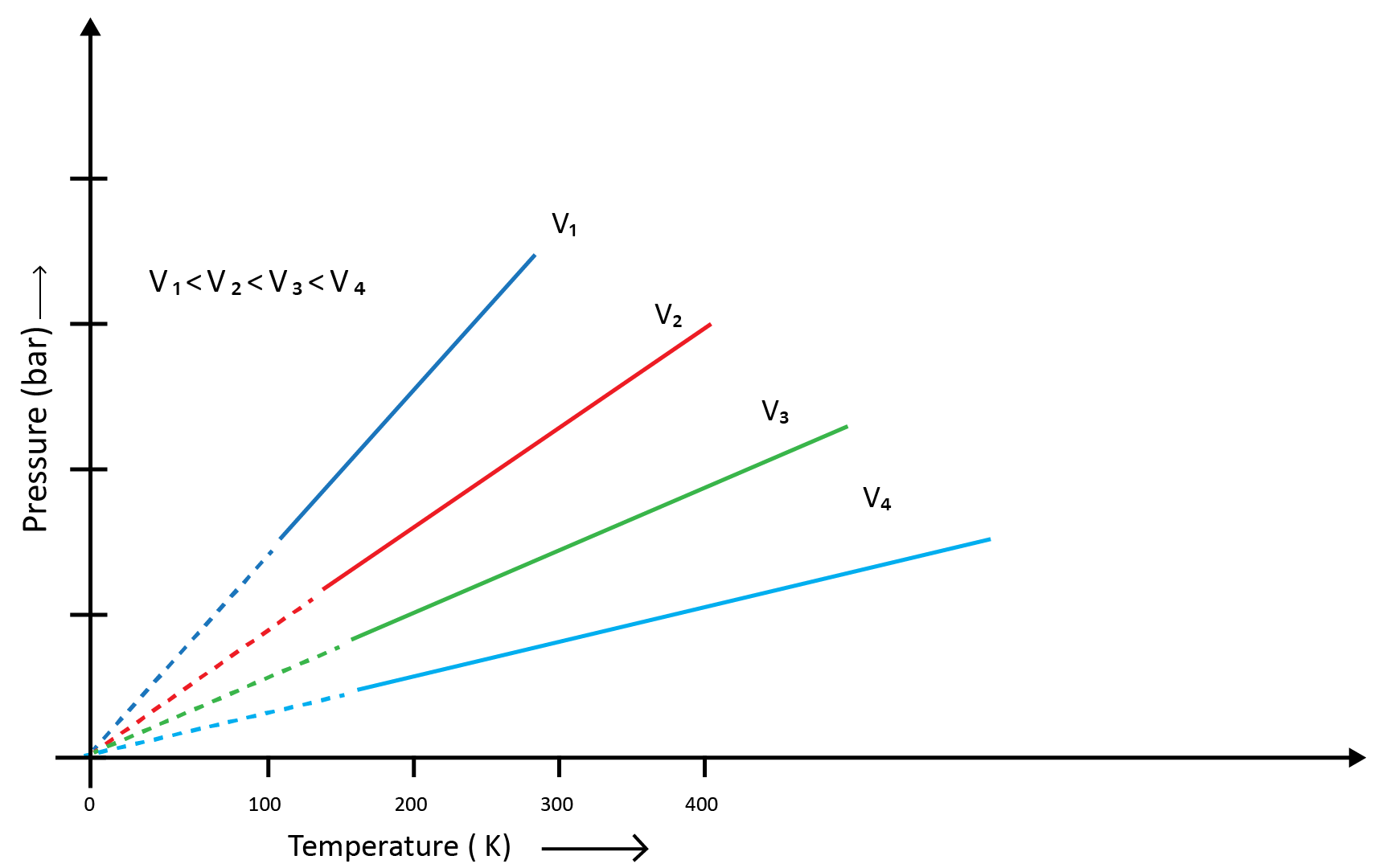
Boyle's and Charles' laws can be used to draw this relationship. The above  graph of pressure vs. temperature (Kelvin) at constant molar volume. Isochore refers to each line in the above graph.

(d) Avogadro Law (Volume - Amount Relationship)

It says that under the same temperature and pressure, identical volumes of all gases contain the same number of molecules. This means that the volume of a gas is determined by the number of molecules in the gas, or the amount of gas, as long as the temperature and pressure remain constant. Mathematically-

V1/n1=V2/n2

(e) Graham's Law of Diffusion

Graham's law of diffusion is a foundational principle in chemistry. For JEE Main aspirants, it holds crucial significance, serving as a key tool in comprehending gas behavior and kinetics. The law states that the rate of diffusion or effusion of a gas is inversely proportional to the square root of its molar mass, represented as $\frac{1}{2} = \frac{2}{1} \quad \frac{R_1}{R_2} = \frac{M_2}{M_1}$. This knowledge aids in predicting gas behavior, calculating relative effusion rates, and determining molecular weights. JEE Main questions often challenge candidates to apply Graham's law when comparing gas diffusion rates, offering a practical application of this fundamental concept in the examination.

6. Ideal Gas Equation 

The three laws ( Boyle's law, Charles law, Avogadro's law) that we've learned so far can be merged into a single equation known as the ideal gas equation-

pV=nRT

R is called gas constant. It is the same for all gases. Hence,  it is also called Universal Gas Constant.

(a) Density and Molar Mass of a Gaseous Substance

The relation is written below-

d/M = P/RT

where d is the density.

(b) Dalton’s Law of Partial Pressures

John Dalton drafted the legislation in 1801. It asserts that the overall pressure exerted by a mixture of non-reactive gases is equal to the sum of individual gas partial pressure.

7.  Kinetic Theory and Molecular Speeds

• Gas molecules are constantly moving. They crash with each other and the container's walls as they move. As a result, their speed changes and energy is redistributed. As a result, the speed and energy of all the gas molecules at any given time are not the same.

• The true distribution of molecular speeds in a gas is dependent on temperature and molecule mass, as demonstrated by Maxwell and Boltzmann.

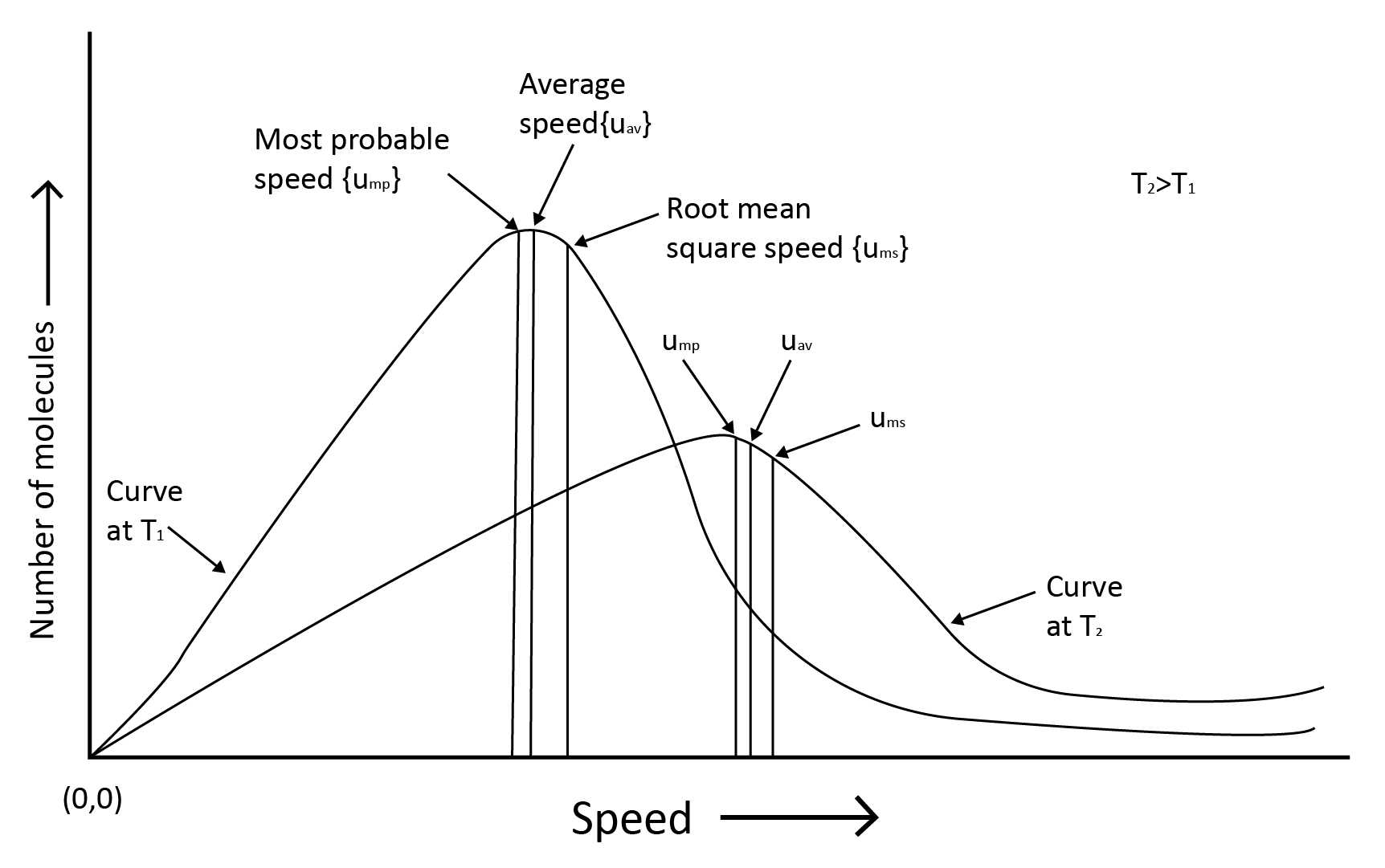
• Root mean square speed, average speed and the most probable speed have the relationship:  urms > uav > ump

8. Kinetic Theory of Gases 

The postulates are given below-

1. Gases include a huge number of microscopic particles.

2. A gas exerts pressure on an object.

3. There is no kinetic energy loss.

4. Gas molecules are attracted to one another.

5. The molecule's kinetic energy is proportional to its absolute temperature.

6. The gaseous molecule's actual volume is relatively small.

7. Gaseous molecules are always moving.

8. Gravity has a greater impact on the movement of gaseous molecules.

9. Behaviour of Real Gases

When a pressure v/s volume plot is drawn, deviation from optimal behaviour is also visible. The experimental pressure vs volume plot (actual gas) and the theoretical pressure v/s volume plot (ideal gas) should be identical. This graph is shown below. The measured volume is clearly greater than the calculated amount at very high pressure.

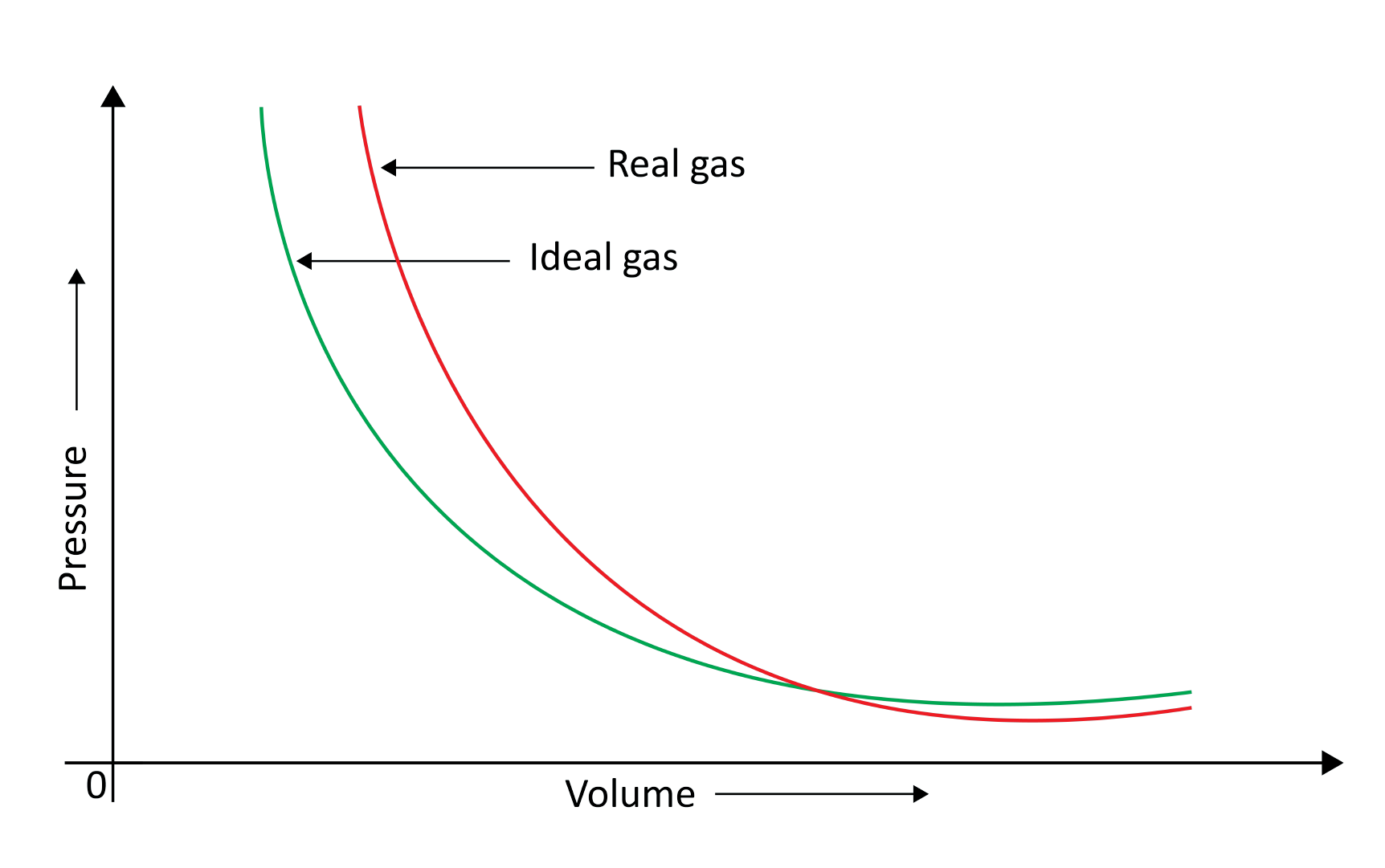
Because molecules interact with one another, real gases deviate from the ideal gas law.

At high pressures, gas molecules are extremely near to one another. Molecular interactions begin to take place. Molecules do not strike the container walls with full power at high pressure because they are pulled back by other molecules due to molecular attraction forces.

• This has an impact on the pressure that molecules exert on the container's walls. As a result, the pressure exerted by the gas is lower than that of the ideal gas.

• The compressibility factor Z, which is the ratio of product pV and nRT, can be used to calculate the departure from ideal behaviour.

Z =pV/nRT is a mathematical formula.

Because pV = nRT, Z = 1 for an ideal gas at all temperatures and pressures. The value of Z deviates from unity for gases that deviate from ideality. All of the gases presented have Z =1 and behave like ideal gases at very low pressures. At high pressure, all gases have a Z>1. Compressing these is more challenging. Most gases have Z<1 at moderate pressures.

10. Liquefaction of Gases

Andrews noted that isotherms at high temperatures resemble those of an ideal gas and that the gas cannot be liquefied even at very high pressure. The shape of the curve varies as the temperature drops, and the data shows a significant divergence from optimal behaviour. Carbon dioxide remains a gas up to 73-atmosphere pressure at 30.98°C (point E.) Liquid carbon dioxide occurs for the first time at 73 atmosphere pressure. The temperature of 30.98°C is known as the carbon dioxide critical temperature. This is the temperature at which liquid carbon dioxide can be found. It is gas above this temperature. Critical volume and critical pressure are terms used to describe the volume of one mole of a gas at a critical temperature.

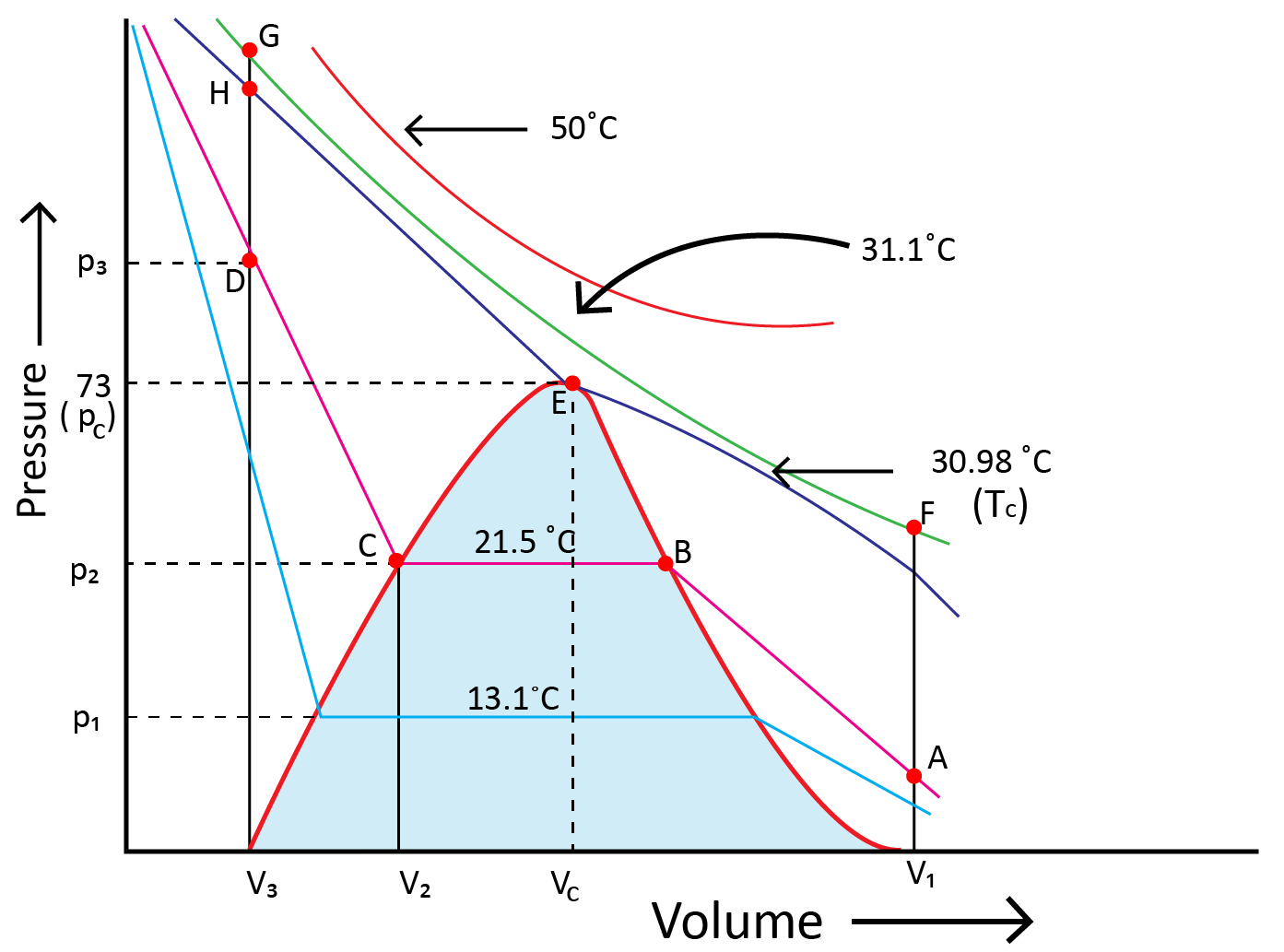
11. Liquid State

In the liquid state, intermolecular forces are stronger than in the gaseous state. Liquid molecules are so close together that there is very little empty space between them, thus liquids are denser than gases under typical conditions. Liquid molecules are held together by intermolecular forces that are attractive. Because molecules do not split from one another, liquids have a defined volume.

(a) Vapour Pressure

If a partially filled evacuated container is a liquid in which a portion of the liquid evaporates in order to replenish the container's remaining volume with vapour. The liquid evaporates at first, and pressure is placed on the walls of a vessel by vapours The pressure inside the container (vapour pressure) rises. After that, It eventually settles into a steady state, and a state of equilibrium is established between the liquid and solid phases  and phase of vaporisation At this point, the vapour pressure is high. Vapour pressure at this stage is called equilibrium vapour pressure or saturated vapour pressure.

(b) Surface Tension

• Surface tension is the tendency of liquid surfaces to shrink to the smallest possible surface area while they are at rest.

• In the bulk of a liquid, a molecule is subjected to equal intermolecular forces from all sides. As a result, the molecule is not subjected to any net force. However, the net attractive force for a molecule on a liquid's surface is towards the liquid's interior.

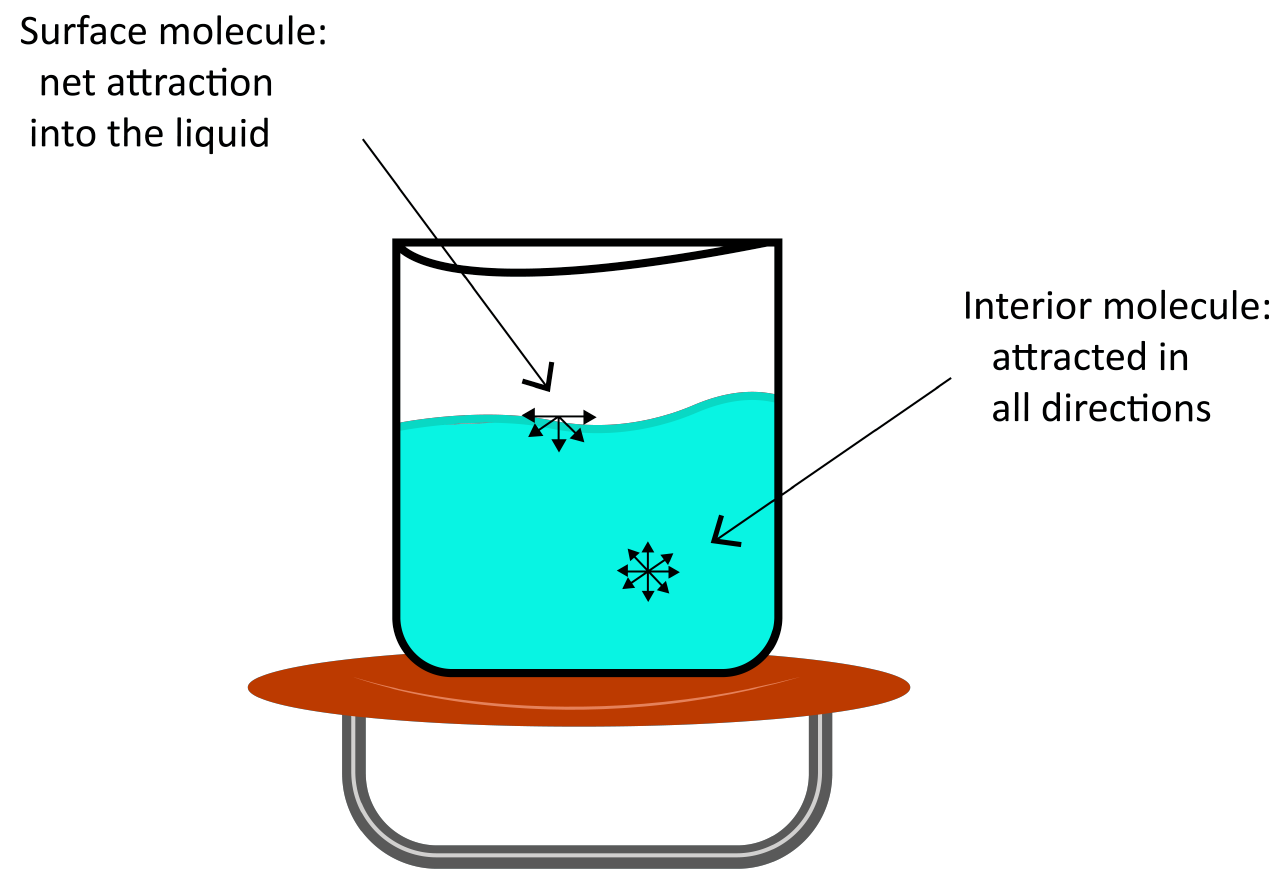
(c) Viscosity

• It is one of the distinguishing characteristics of liquids. Internal friction between layers of fluid as they slip past one another while liquid flows cause viscosity, which is a measure of flow resistance. Strong intermolecular interactions hold molecules together and prevent layers from moving past one another.

• The viscosity of a liquid determines how slowly it moves. The van der Waals and hydrogen bonding forces are strong enough to generate significant viscosity. Glass is a viscous liquid with a high viscosity.

• It has such a high viscosity that many of its properties are similar to those of solids.

• Because at high temperatures, molecules have enormous kinetic energy and can overcome intermolecular interactions to glide past one another between layers, the viscosity of liquids lowers.

Concept of Absolute Scale of Temperature

In the realm of thermodynamics and heat transfer, understanding the concept of an absolute scale of temperature is of utmost importance for JEE Main aspirants. This concept is fundamentally linked to the behavior of gases and forms the basis for solving a wide range of problems in the field. Here's a concise explanation of the concept:

Definition:

An absolute scale of temperature is a temperature scale that has its zero point at absolute zero, the lowest possible temperature theoretically achievable. The Kelvin (K) scale is a prime example of an absolute temperature scale.

Absolute Zero: Absolute zero, denoted as 0 Kelvin (0 K), is the temperature at which the kinetic energy of particles in a substance reaches its minimum possible value. At this point, the particles cease to move, making it the lowest temperature on the absolute scale.

Relation with Celsius: The Kelvin scale is related to the Celsius scale by the equation:

K=°C+273.15

This equation allows for easy conversion between the two scales.

Kinetic Theory of Gases 

The Kinetic Theory of Gases is a fundamental concept in physics and chemistry that describes the behavior of gases at the molecular level. For JEE Main students, a clear understanding of the postulates of this theory is crucial as it forms the basis for solving problems related to gas behavior and thermodynamics. Here are the key postulates:

Gas Consists of Particles: The theory assumes that gases are composed of a large number of tiny particles, either atoms or molecules, that are in constant, random motion.

Negligible Volume of Particles: The volume occupied by the gas particles themselves is considered negligible compared to the total volume of the gas. In other words, gas particles are assumed to be point masses.

Constant, Random Motion: Gas particles are in continuous, rapid, and random motion. They move in straight lines until they collide with each other or the walls of the container.

Elastic Collisions: Collisions between gas particles, or between particles and the walls of the container, are perfectly elastic. This means that kinetic energy is conserved during collisions.

No Interactions Except Collisions: Gas particles exert no attractive or repulsive forces on each other except during collisions. The intermolecular forces are considered negligible.

Average Kinetic Energy: The kinetic energy of gas particles is directly proportional to the absolute temperature (measured in Kelvin) of the gas. This is known as the Kinetic-Molecular Theory Equation: 

\[KE = \frac{3}{2} kT\]

where $KE$ is the kinetic energy, $k$ is the Boltzmann constant, and $T$ is the temperature in Kelvin.

Pressure Due to Collisions: Gas pressure arises from the collisions of gas particles with the walls of the container. The greater the frequency and force of these collisions, the higher the pressure.

Understanding these postulates is essential for JEE Main students as they serve as the foundation for explaining the behavior of ideal gases and solving related problems. The Kinetic Theory of Gases helps in deriving gas laws such as Boyle's Law, Charles's Law, and the Ideal Gas Law, all of which are frequently tested in the JEE Main examination. Additionally, this theory provides insights into the thermodynamic properties of gases, making it a crucial topic for students preparing for the exam.

Liquid

A liquid is a virtually incompressible fluid that conforms to its container's shape while maintaining a (nearly) constant volume regardless of pressure. If the temperature and pressure remain constant, the volume is fixed. When a solid is heated past its melting point and the pressure is greater than the substance's triple point, it becomes liquid. While intermolecular (or interatomic or interionic) forces still exist, the molecules have enough energy to travel about and the structure is mobile. This implies that the form of a liquid is determined by its container rather than the liquid itself. The volume is typically greater than that of the equivalent solid, with water ($H_2O$) being the most well-known exception. The critical temperature of a liquid is the maximum temperature at which it can live. The liquid state of matter is a transition between solid and gaseous states.

Properties of Liquid:

• Liquids are almost impervious to compression. Molecules in liquids are very similar to one another.

• Liquids have a constant volume but no constant form.

• Liquids flow from one stage to the next.

• In normal circumstances, liquids have boiling points that are higher than room temperature.

Vapor Pressure, Viscosity, and Surface Tension: Effects of Temperature

In the realm of fluid mechanics and thermodynamics, three essential properties come into play when studying the behavior of liquids and gases: vapor pressure, viscosity, and surface tension. These properties have a profound influence on various natural and industrial processes. Here, we'll explore how temperature impacts these properties qualitatively.

1. Vapor Pressure:

Vapor pressure is the pressure exerted by a vapor when it is in equilibrium with its liquid phase. It is a fundamental property that plays a crucial role in phase transitions and chemical reactions. The effect of temperature on vapor pressure is described by Raoult's law, which states that the vapor pressure of a component in a liquid mixture is directly proportional to its mole fraction and temperature.

Qualitatively, as temperature increases:Vapor pressure also increases.

More molecules gain enough energy to break free from the liquid phase and enter the vapor phase.

Liquids evaporate more rapidly at higher temperatures.

For example, a pot of water boils faster on a hot stove compared to a colder one because the higher temperature increases the vapor pressure of water, making it easier for bubbles to form and the liquid to boil.

2. Viscosity:

Viscosity is a measure of a fluid's resistance to flow. It depends on the internal friction between the molecules of the fluid. In most cases, temperature and viscosity are inversely proportional.

Qualitatively, as temperature increases: Viscosity decreases.

The kinetic energy of the molecules in the fluid increases, causing them to move more rapidly.

This increased motion reduces the internal friction, making the fluid flow more easily.

For instance, honey flows more slowly when it's cold because its viscosity is higher. On a hot day, honey flows more easily because the increase in temperature reduces its viscosity.

3. Surface Tension:

Surface tension is the tendency of a liquid's surface to minimize its area, creating a "skin" or surface layer due to intermolecular forces. Temperature also has a qualitative effect on surface tension.

Qualitatively, as temperature increases: Surface tension decreases.

Molecules at the surface gain more kinetic energy and move more vigorously.

This increased motion weakens the cohesive forces at the surface, reducing surface tension.

Consider a soap bubble. On a warm day, soap bubbles tend to pop more easily because the higher temperature reduces the surface tension, causing the bubble's thin film to weaken.

Solid State: Classification of Solids and Bragg's Law

The solid state of matter is a fascinating area of study in chemistry and materials science. It encompasses a wide variety of substances with distinct properties, structures, and behaviors. In this overview, we will delve into the classification of solids, the concept of Bragg's Law, and its applications.

Classification of Solids:

Solid-state materials can be broadly categorized into four main types based on the nature of the chemical bonds and the arrangement of particles:

Molecular Solids: In molecular solids, such as ice (H2O) or sugar (C12H22O11), the constituent particles are discrete molecules held together by weak van der Waals forces or hydrogen bonds. These solids are typically soft and have low melting points due to the weak intermolecular forces.

Ionic Solids: Ionic solids, like sodium chloride (NaCl) or potassium iodide (KI), consist of positively and negatively charged ions arranged in a three-dimensional lattice. The strong electrostatic forces between ions give rise to high melting points and good electrical conductivity when molten or dissolved.

Covalent Solids: Covalent solids, such as diamond (composed of carbon atoms) or silicon dioxide (SiO2), feature a network of covalent bonds between the atoms. These solids are exceptionally hard, have high melting points, and are poor conductors of electricity.

Metallic Solids: Metallic solids, exemplified by materials like copper (Cu) or iron (Fe), are composed of a closely packed arrangement of positively charged metal ions surrounded by a "sea" of delocalized electrons. This structure gives rise to high electrical conductivity, malleability, and ductility.

Additionally, solids can be classified as either amorphous or crystalline based on the arrangement of their constituent particles. Amorphous solids lack a regular, repeating atomic or molecular structure, while crystalline solids have a highly ordered and repetitive lattice arrangement.

Bragg's Law and Its Applications:

Bragg's Law is a fundamental concept in the study of crystallography. It relates the angles at which X-rays are diffracted by the crystal lattice to the spacing between the crystal planes. The law can be represented as:

\[n\lambda = 2d\sin(\theta)\]

Where:

n - is an integer representing the order of the diffraction.

$\lambda$ is the wavelength of the X-rays.

d - the spacing between the crystal planes.

$\theta$ - the angle of incidence.

Applications of Bragg's Law include:

Determination of Crystal Structures: X-ray crystallography is widely used to determine the three-dimensional atomic or molecular structure of crystalline solids, including complex biological molecules like proteins and DNA.

Materials Characterization: Scientists use X-ray diffraction to identify and characterize the structure of various materials, including minerals, metals, ceramics, and polymers.

Quality Control: Bragg's Law is employed in quality control processes to assess the purity and composition of materials, particularly in the pharmaceutical and semiconductor industries.

Unit Cell and Lattices:

In crystalline solids, the basic repeating structural unit is called the "unit cell." Different types of unit cells combine to form various lattice structures, including face-centered cubic (FCC), body-centered cubic (BCC), and hexagonal close-packed (HCP) lattices. These lattice structures determine the physical properties of the solid, such as density, electrical conductivity, and mechanical strength.

Voids and Imperfections:

In crystalline solids, there are often vacant spaces or voids within the lattice. Imperfections in the crystal structure, such as vacancies, dislocations, and grain boundaries, can significantly affect material properties, including mechanical strength and electrical conductivity.

Electrical and Magnetic Properties:

The electrical and magnetic properties of solids are highly dependent on their composition, structure, and defects. Conductors, semiconductors, and insulators are broad categories of materials based on their electrical conductivity. Magnetic properties can range from diamagnetism (repelled by a magnetic field) to ferromagnetism (strongly attracted to a magnetic field) and everything in between.

Solved Examples from the Chapter

Example 1: Calculate the compressibility factor for CO2, if one mole of it occupies 0.4 litre at 300K and 40 atm. Comment on the result.    

Solution: Compressibility factor (Z) = PV / nRT  

Z = 40 × 0.4 / 1 × 0.0821 × 300 = 0.65  

As, the Z value is lesser than 1 and thus, nRT > PV. In order to have Z = 1, volume of CO2 must have been more at the same P and T or CO2 is more compressible than ideal gas.

Key point to remember:The compressibility factor Z, which is the ratio of product  of pV and nRT, can be used to calculate the departure from ideal behaviour.

Example 2: How large a balloon can you fill with 4g of He gas at 22°C and 720 mm of Hg?

Solution: Given, P = 720 / 760 atm, T = 295K, w = 4g  and M = 4 for He  

PV = w / M RT   = 720 / 760 × V = 4/4 × 0.0821 × 295  

Therefore, V = 25.565 litre.

Key point to remember: Ideal gas equation that is pV=nRT.

Solved Examples from Previous Year’s Questions

Question 1: Which intermolecular force is most responsible for allowing xenon gas to liquefy?

(1) Instantaneous dipole induced dipole

(2) Ion dipole

(3) Ionic

(4) Dipole-dipole

Solution: For the liquefaction of xenon, instantaneous dipole induced dipole forces are responsible.

Therefore, option (1) is the answer.

Trick: As Xenon is an inert gas, we can do its liquefaction and for the liquefaction instantaneous dipole induced dipole forces are responsible.

Question 2: Kinetic theory of gases proves

(1) Only Boyle's law

(2) Only Charle’s law

(3) Only Avogadro’s law

(4) all of these

Solution: One of the postulates of the kinetic theory of gases is average kinetic energy proportional to T. This theory proves all the above-given laws.

Therefore,  option (4) is the answer.

Trick: Postulates of the kinetic theory of gases gives a clear idea about the gas molecules and proves all the gas laws.

Question 3:  According to the kinetic theory of gases, in an ideal gas, between two successive collisions a gas molecule travels

(1) In a circular path

(2) In a wavy path

(3) In a straight-line path

(4) with an accelerated velocity

Solution: According to the kinetic theory of gases, in an ideal gas, between two successive collisions a gas molecule travels in a straight-line path.

Therefore,  option (3) is the answer

Trick: Postulates of the kinetic theory of gases give a clear idea about the gas molecules and also about their nature.

Practice Questions

1. The temperature at which oxygen molecules have the same root mean square  speed as helium atoms have at 300 K is :

(Atomic masses : He = 4 u, O = 16 u)

(1) 1200 K

(2) 600 K

(3) 300 K

(4) 2400 K

Answer: (4) 2400 K

Question 2: A pressure cooker reduces cooking time for food as-

(1) Heat is more evenly distributed in the cooking space.

(2) Boiling point of water involved in cooking is increased

(3) The higher pressure inside the cooker crushes the food.

(4) Cooking involves chemical changes helped by a rise in temperature.

Answer: (2) Boiling point of water involved in cooking is increased.

JEE Main States of Matter Study Materials

Here, you'll find a comprehensive collection of study resources for States of Matter designed to help you excel in your JEE Main preparation. These materials cover various topics, providing you with a range of valuable content to support your studies. Simply click on the links below to access the study materials of States of Matter and enhance your preparation for this challenging exam.

JEE Main Chemistry Study and Practice Materials

Explore an array of resources in the JEE Main Chemistry Study and Practice Materials section. Our practice materials offer a wide variety of questions, comprehensive solutions, and a realistic test experience to elevate your preparation for the JEE Main exam. These tools are indispensable for self-assessment, boosting confidence, and refining problem-solving abilities, guaranteeing your readiness for the test. Explore the links below to enrich your Chemistry preparation.

Conclusion

Intermolecular forces exist between matter particles. Pure electrostatic forces exist between two oppositely charged ions, but these forces are different. These forces do not include the covalent bonds that hold atoms in a covalent molecule together. The state of matter is determined by the competition between thermal energy and intermolecular interactions. The energy of constituent particles and the sort of interaction between them determine "bulk" qualities of matter such as gas behaviour, solids and liquids characteristics, and state change. The chemical qualities of a substance do not change as a result of its physical state, but reactivity does.

Important Related Links for JEE Main 2023-24