




Stepwise Derivation of De Broglie Equation with Examples
The De Broglie Relationship is a cornerstone topic in JEE Main Chemistry, describing how every moving particle, like an electron, shows both wave-like and particle-like properties. Proposed by Louis de Broglie in 1924, it bridged classical and quantum views by suggesting all matter has an associated wavelength. This concept explains crucial quantum effects seen in atomic structure, electron movement, and the limits of classical physics.
De Broglie Relationship: The Principle of Matter Waves
According to the De Broglie Relationship, any particle with mass and velocity behaves as a wave in certain conditions. The wavelength associated with such a particle is given by the De Broglie equation:
- λ = h / p (where λ is the wavelength, h is Planck’s constant, and p is momentum, p = mv).
- This is known as the De Broglie wavelength formula.
- It unifies Einstein’s and Planck’s approaches to quantum matter.
- JEE Main frequently asks definition, applications, and numericals of this formula.
For the special case of an electron, the De Broglie Relationship reveals its quantum behavior, influencing properties like atomic orbitals and chemical bonding. Because mass of macroscopic objects is large, their λ becomes almost zero, so wave nature is negligible—crucial for exam application and conceptual clarity.
Stepwise Derivation of De Broglie Equation
JEE Main requires a clear, step-by-step De Broglie Relationship derivation, drawing from Einstein’s and Planck’s equations.
- For light (photon): Planck’s relation: E = hν, where E = energy, h = Planck’s constant, ν = frequency.
- For matter: Einstein’s relation: E = mc2, where m = mass, c = speed of light.
- Equating the two energies (using v for velocity of the particle): E = hν = mv2.
- Frequency ν relates to wavelength λ and velocity: ν = v / λ.
- Substitute ν: h(v / λ) = mv2 ⇒ h / λ = mv.
- Rearrange: λ = h / (mv) = h / p.
Where λ is de Broglie wavelength (in metres), h is Planck’s constant (6.626 × 10-34 J·s), m is mass (kg), v is velocity (m/s), and p is momentum (kg·m/s). Ensure SI units for all JEE Main calculations.
Physical Significance and JEE Applications
The major significance of the De Broglie Relationship is that it introduces the wave-particle duality concept for all matter—even electrons, neutrons, atoms, and molecules. This directly supports:
- Quantum models of atom and electron configuration.
- Electron diffraction (evidence for wave nature of electrons).
- The foundation for Heisenberg’s uncertainty principle.
- Key to explaining chemical bonding, periodic properties, and atomic spectra.
- Why macroscopic objects (balls, cars) do NOT show observable wave effects—their de Broglie wavelengths are extremely small.
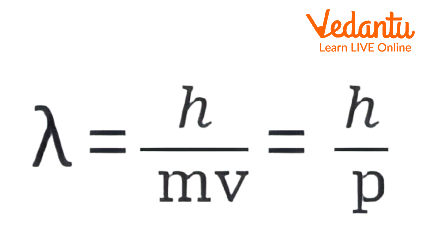
A higher velocity or greater mass yields a smaller wavelength. For atomic-scale particles (like electrons), λ is measurable, but for everyday objects it is negligible. Understanding these distinctions is vital for scoring in atomic structure and quantum theory sections.
Table: De Broglie Equation Details
| Term | Symbol | SI Unit |
|---|---|---|
| De Broglie Wavelength | λ | metre (m) |
| Planck’s Constant | h | Joule-second (J·s) |
| Momentum | p (mv) | kilogram metre per second (kg·m/s) |
Typical exam trap: forgetting mass must be in kg, velocity in m/s, and h in SI for correct λ calculation. Always check your units.
Solved Example: De Broglie Wavelength Calculation
Example: Find the De Broglie wavelength of an electron moving at 2.0 × 106 m/s. (me = 9.11 × 10-31 kg, h = 6.626 × 10-34 J·s)
- λ = h / (mv) = 6.626 × 10-34 / (9.11 × 10-31 × 2.0 × 106)
- = 6.626 × 10-34 / 1.822 × 10-24 = 3.63 × 10-10 m
So the De Broglie wavelength is 3.63 × 10-10 m. This is comparable to inter-atomic spacings, explaining why electron waves can create diffraction patterns, unlike macroscopic bodies.
Key Points, Pitfalls, and Exam Usage
- Only microscopic particles (like electrons) show significant de Broglie wavelengths—the formula supports "wave-particle duality."
- All symbols in λ = h / (mv) must use SI units; otherwise, answers will be numerically incorrect.
- Large objects (football, bus) have λ so small that quantum effects are never seen practically.
- Common JEE question: compare or calculate λ for an electron, proton, neutron, etc. at given velocities.
- Concept directly connects to quantum models, atomic spectra, and chemical bonding questions.
- Atomic structure tests often combine De Broglie theory and wave-particle duality.
Carefully distinguish the De Broglie equation from other wave equations in physics topics. Link it to quantum chemistry sections such as Chemical Bonding and Atomic Structure for revision.
Further Connections and Learning Resources
- Connect to atomic model revision for integrating De Broglie’s contributions with Schrödinger's wave mechanics.
- Practice basic chemistry concepts to strengthen fundamental understanding of mass, velocity, and SI units in context.
- Explore more with atomic structure important questions and JEE Main question answers.
- To see De Broglie in chemical systems, revise bonding theory and molecular orbital theory.
JEE toppers suggest not just memorising the De Broglie Relationship, but understanding its physical relevance and correctly applying it in comparison and calculation-based problems. For more expert notes and practice material, explore Vedantu’s complete JEE Chemistry Topic Library.
FAQs on De Broglie Relationship Explained: Concept, Formula & Uses
1. What is De Broglie relationship?
The De Broglie relationship states that every moving particle has an associated wavelength given by the formula λ = h/p, where λ is wavelength, h is Planck’s constant, and p is the momentum of the particle. This relationship shows that particles like electrons and protons exhibit both wave and particle nature (wave–particle duality). Key points:
- λ = h/p
- Applies to all matter, especially microscopic particles
- Foundation for quantum mechanics and atomic theory
2. What is the De Broglie equation in chemistry?
In chemistry, the De Broglie equation expresses the wavelength (λ) of a particle as λ = h/mv, where m is mass and v is velocity. It explains the wave nature of tiny particles like electrons in atoms.
- λ = h / (mv) for particles with mass m and velocity v
- Used to calculate wavelengths of electrons in shells/subshells
- Essential for understanding orbitals and quantum numbers in class 11 syllabus
3. What is the formula for De Broglie wavelength?
The De Broglie wavelength formula is λ = h/p, where λ is wavelength, h is Planck’s constant (6.626 x 10-34 Js), and p is momentum. For an electron or particle with mass m moving at velocity v, it becomes λ = h/(mv). Main formulae:
- λ = h/p
- λ = h/(mv)
- Units: λ in meters (m), h in Joule·seconds (Js), p in kg·m/s
4. Who gave the De Broglie hypothesis?
The De Broglie hypothesis was proposed by the French physicist Louis de Broglie in 1924. He suggested that all matter has both particle and wave properties. Key facts:
- Name: Louis de Broglie
- Year: 1924
- Awarded the Nobel Prize in Physics in 1929 for this discovery
5. What is the significance of the De Broglie equation?
The De Broglie equation is significant because it explains the dual nature of matter and helped develop modern quantum mechanics. Highlights include:
- Justifies the wave-like properties of electrons in atoms
- Explains observed phenomena like electron diffraction
- Leads to the quantum mechanical model of the atom
- Reveals why macroscopic objects do not show measurable wavelengths
6. How do you derive the De Broglie wavelength?
The De Broglie wavelength is derived by equating the energy expressions for photons and matter waves. Steps:
- For a photon: λ = h/p, where p = momentum
- For a particle: p = mv (mass x velocity)
- Substitute to get: λ = h/(mv)
- This shows the wavelength associated with any moving particle
7. Does the De Broglie wavelength apply to macroscopic (large) objects?
The De Broglie wavelength applies to all matter, but for large objects the wavelength is negligibly small and thus unobservable. For example:
- Microscopic particles (electrons) have measurable wavelengths
- Macroscopic bodies (like a football) have wavelengths too tiny to detect
8. Can the De Broglie relation explain why electrons show diffraction but not footballs?
Yes, the De Broglie relation explains that diffraction patterns are only visible for objects with sufficiently large wavelengths—like electrons—not macroscopic objects like footballs.
- Wavelength inversely depends on mass and velocity (λ = h/mv)
- Electrons have small mass, so their λ is significant
- Large objects have near-zero λ, so no observable diffraction
9. Is the De Broglie equation valid for light (photons)?
The De Broglie equation also applies to photons and all particles, with λ = h/p for photons since they have momentum but zero rest mass. Details:
- Photons: p = h/λ, rearranged as λ = h/p
- This is identical to the De Broglie formula
- Shows wave-particle duality for light as well
10. What mistakes do students make when using the De Broglie formula in numericals?
Common mistakes with the De Broglie formula include using incorrect units or formula selection. To avoid errors:
- Always use SI units (kg for mass, m/s for velocity)
- Ensure Planck’s constant h is in Joule·seconds (Js)
- Check if the particle is at rest (λ not defined) or moving
- Apply the right formula for charged vs. uncharged particles
11. How is De Broglie’s idea related to the quantum mechanical model of the atom?
De Broglie’s idea of matter waves is fundamental to the quantum mechanical model of the atom, explaining electron orbitals as standing waves. Main connections:
- Introduces quantization of angular momentum for electrons
- Predicts stable orbits where electron wavelength fits a whole number of times
- Forms the basis for atomic orbital shapes and quantum numbers

































