Important Questions for CBSE Class 11 Physics Chapter 5 - Work, Energy and Power

Very Short Answer Questions                                                                         1 Mark

1. If two bodies stick together after collision, will the collision be elastic or inelastic?

Ans: If two bodies stick together after the collision the collision will be an inelastic collision.

2. When an air bubble rises in water, what happens to its potential energy?

Ans: When an air bubble rises in water, the potential energy of the air bubble decreases because work is done by upthrust on the bubble.

3. A spring is kept compressed by pressing its ends together lightly. It is then placed in a strong acid, and released. What happens to its stored potential energy?

Ans: When spring is kept compressed by pressing its ends together lightly and further placed in strong acid and released, the loss in potential energy appears as kinetic energy of the molecules of the acid.

4. Define the triple point of water.

Ans: Triple point of water indicates the values of pressure and temperature at which water co-exists in equilibrium in all the three states of matter.

5. State Dulong and Petit law.

Ans: According to Dulong and Petit law, the specific heat of all the solids is constant at room temperature and is equal to \[3R\].

6. Why are the clock pendulums made of invar, a material of low value of coefficient of linear expansion?

Ans: The clock pendulums are made of Inver as it has a low value of α (coefficient of linear expansion) i.e., for a small change in temperature, there won’t be much change in the length of the pendulum.

7. Why is mercury used in making thermometers?

Ans: Mercury is used in making thermometers as it has a wide and useful temperature range and has a uniform rate of expansion.

8. How would a thermometer be different if glass expanded more with increasing temperature than mercury?

Ans: If glass expanded more with increasing temperature than mercury, the scale of the thermometer would be upside down.

9. Show the variation of specific heat at constant pressure with temperature.

Ans: Here is the required variation:

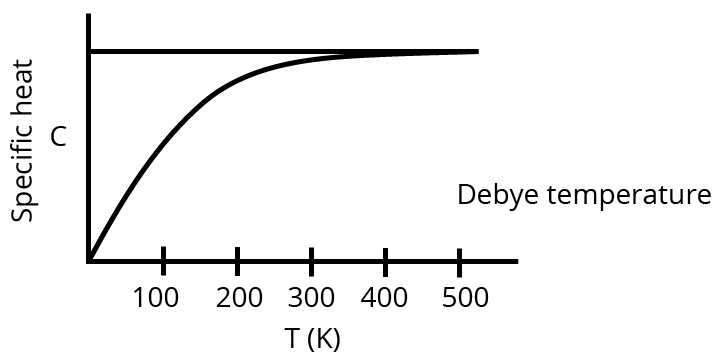
10. Two thermometers are constructed in the same way except that one has a spherical bulb and the other an elongated cylindrical bulb. Which one will respond quickly to temperature change?

Ans: The thermometer with a cylindrical bulb will respond quickly to temperature changes as the surface area of the cylindrical bulb is greater than that of a spherical bulb.

11. A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by \[F=-\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\,N\]. Where \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,,\overset{\wedge }{\mathop{k}}\,\] are unit vectors along the x, y and z axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z axis?

Ans: Force exerted on the body is \[F=-\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\,N\].

Displacement, \[s\text{ }=4\overset{\wedge }{\mathop{k}}\,\text{ }m\]

Work done, \[W\text{ }=F.s\]

\[=\left( -\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\, \right).\left( 4\overset{\wedge }{\mathop{k}}\, \right)\]

$=12\text{ }J$

Thus, \[12\text{ }J\] of work is done by the force on the body.

12. A molecule in a gas container hits a horizontal wall with speed and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?

Ans: Yes; the collision is elastic. The momentum of the gas molecule remains conserved whether the collision is elastic or inelastic. The gas molecule moves with a velocity of \[200\text{ }m/s\] and strikes the stationary wall of the container and rebounds with the same speed. This shows that the rebound velocity of the wall remains zero. Thus, the total kinetic energy of the molecule remains conserved during the collision. The given collision is an example of an elastic collision.

13. The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.15. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

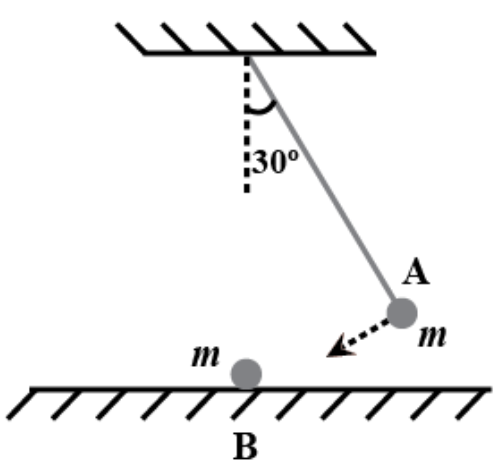
Ans: Bob A won’t rise at all. For an elastic collision between two equal masses in which one is stationary, while the other is moving with some velocity, the stationary mass acquires the same velocity, while the moving mass immediately comes to rest after collision. Here a complete transfer of momentum takes place from the moving mass to the stationary mass. Thus, bob A of mass m, will come to rest after colliding with bob B of equal mass, while bob B will move with the velocity of bob A at the instant of collision.

14. A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg/s. What is the speed of the trolley after the entire sand bag is empty?

Ans: The sand bag is placed on a trolley that is moving with a uniform speed of \[27\text{ }km/h\]. The external forces acting on the system of the sandbag and the trolley is zero. As the leaking action does not produce any external force on the system, the sand starts leaking from the bag with no change in the velocity of the trolley. This is in accordance with Newton's first law of motion. Thus, the speed of the trolley will remain \[27\text{ }km/h\].

15. Which of the following potential energy curves in Fig. 6.18 cannot possibly describe the elastic collision of two billiard balls? Here r is the distance between centres of the balls.

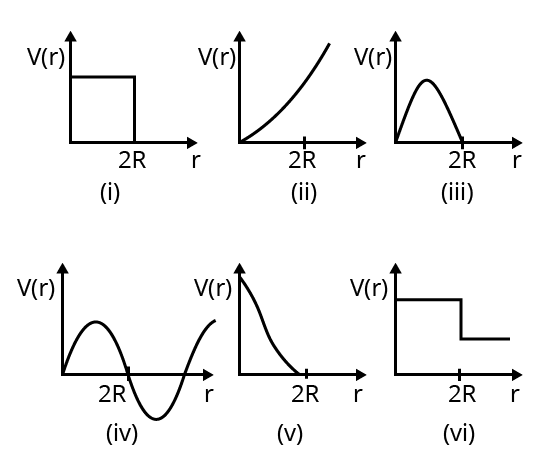
Ans:  From the figure given in the question, (i), (ii), (iii), (iv), and (vi) cannot possibly describe the elastic collision of two billiard balls. We know that the potential energy of a system of two masses is inversely proportional to the separation between them. Here the potential energy of the system of the two balls will decrease as they come closer to each other. It will become zero (i.e., \[V\left( r \right)\text{ }=\text{ }0\]) when the two balls touch each other, i.e., at \[r\text{ }=\text{ }2R\], where R is the radius of each billiard ball. The potential energy curves given in figures (i), (ii), (iii), (iv), and (vi) do not satisfy these two conditions. Thus, they do not describe the elastic collisions between them.

Short Answer Questions                                                                                2 Marks

1. A body is moving along Z – axis of a co – ordinate system is subjected to a constant force F is given by $\overset{\to }{\mathop{F}}\,=-\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\,N$. Where \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,,\overset{\wedge }{\mathop{k}}\,\] are unit vector along the x, y and z – axis of the system respectively. What is the work done by this force in moving the body a distance of 4m along the Z – axis?

Ans: Force exerted on the body is,

 \[F=-\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\,N\].

Displacement, \[s\text{ }=4\overset{\wedge }{\mathop{k}}\,\text{ }m\]

Work done, \[W\text{ }=F.s\]

\[=\left( -\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\, \right).\left( 4\overset{\wedge }{\mathop{k}}\, \right)\]

$=12\text{ }J$

Thus, \[12\text{ }J\] of work is done by the force on the body.

2. A ball is dropped from the height \[{{h}_{1}}\] and if re-bounces to a height \[{{h}_{2}}\]. Find the value of coefficient of restitution.

Ans: As the ball drops from height \[{{h}_{1}}\],

Velocity of approach will be ${{v}_{1}}=\sqrt{2g{{h}_{1}}}$

And the ball rebounds to height \[{{h}_{2}}\].

Therefore, velocity of separation is ${{v}_{2}}=\sqrt{2g{{h}_{2}}}$

Coefficient of restitution is given by:

$e=\frac{{{v}_{2}}}{{{v}_{1}}}=\frac{\sqrt{2g{{h}_{2}}}}{\sqrt{2g{{h}_{1}}}}$

$\Rightarrow e=\sqrt{\frac{{{h}_{2}}}{{{h}_{1}}}}$

3. State and prove work energy theorem analytically.

Ans: The work-energy theorem states that work done by force acting on a body is equal to the change produced in its kinetic energy.

If $\vec{F}$ force is applied to move an object through a distance $d\vec{s}$.

Then $dw=\vec{F}.d\vec{s}$

$F=m\vec{a}$

$dw=m\vec{a}.d\vec{s}$

$dw=m\frac{d\vec{v}}{dt}.d\vec{s}$

\[dw=m\frac{d\vec{s}}{dt}.d\vec{v}\]

\[\Rightarrow dw=mv.d\vec{v}\]

On integrating,

\[\sum{dw}=W=\int\limits_{u}^{v}{mv.d\vec{v}}\]

\[W=m\left| \frac{v}{2} \right|_{u}^{v}\]

\[\Rightarrow W=\frac{m{{v}^{2}}}{2}-\frac{m{{u}^{2}}}{2}\]

Hence \[W\text{ }=\text{ }{{K}_{f}}\text{ }\text{ }{{K}_{i}}\] Where \[{{K}_{f}}\] and \[{{K}_{i}}\] are final and initial kinetic energy.

4. An object of mass 0.4kg moving with a velocity of 4m/s collides with another object of mass 0.6kg moving in the same direction with a velocity of 2m/s. If the collision is perfectly inelastic, what is the loss of K.E. due to impact?

Ans: In the above question it is given that:

\[{{m}_{1\text{ }}}=\text{ }0.4kg\],

\[{{u}_{1}}\text{ }=\text{ }4m/s\], 

\[{{m}_{2\text{ }}}=\text{ }0.6kg\] And

\[{{u}_{2\text{ }}}=\text{ }2m/s\].

Total K.E. before collision is given by:

${{K}_{i}}=\frac{1}{2}{{m}_{1}}{{u}_{1}}^{2}+\frac{1}{2}{{m}_{2}}{{u}_{2}}^{2}$

\[\Rightarrow {{K}_{i}}=\frac{1}{2}\left( 0.4 \right){{\left( 4 \right)}^{2}}+\frac{1}{2}\left( 0.6 \right){{\left( 2 \right)}^{2}}\]

\[\Rightarrow {{K}_{i}}=4.4J\]

Since collision is perfectly inelastic,

$v=\frac{{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}}{{{m}_{1}}+{{m}_{2}}}=2.8m/s$

Total K.E. after collision is given by:

${{K}_{f}}=\frac{1}{2}\left( {{m}_{1}}+{{m}_{2}} \right){{v}^{2}}$

$\Rightarrow {{K}_{f}}=\frac{1}{2}\left( 0.4+0.6 \right){{2.8}^{2}}$

$\Rightarrow {{K}_{f}}=3.92J$

Thus, loss in K.E. will be:

$\Delta K={{K}_{i}}-{{K}_{f}}$

$\Rightarrow \Delta K=4.4-3.92=0.48J$

5. Why does the density of solid/liquid decreases with rise in temperature?

Ans: Consider P to be Density of solid/liquid at temperature T.

\[{{P}_{1}}\text{ }=\text{ }Density\text{ }of\text{ }solid/liquid\text{ }at\text{ }Temperature\text{ }T+\Delta T\].

As, \[Density=\frac{Mass}{Volume}\]

\[P=\frac{M}{V}\] …… (1)

\[{{P}_{1}}=\frac{M}{{{V}_{1}}}\] …… (2)

\[{{V}_{1}}=\text{ }Volume\text{ }of\text{ }solid\text{ }at\text{ }temperature\text{ }T\text{ }+\text{ }\Delta T\]

\[V\text{ }=\text{ }Volume\text{ }of\text{ }solid\text{ }at\text{ }temperature\text{ }T\]

As on increasing the temperature, solids/liquids expand, that is their volume increases, so by equation 1) & 2) Density is inversely proportional to volumes. Therefore, if the volume increases on increasing the temperature, Density will decrease.

6. Two bodies at different temperatures \[{{\mathbf{T}}_{\mathbf{1}}}\], and \[{{\mathbf{T}}_{\mathbf{2}}}\] are brought in thermal contact do not necessarily settle down to the mean temperature of \[{{\mathbf{T}}_{\mathbf{1}}}\] and \[{{\mathbf{T}}_{\mathbf{2}}}\]. Why?

Ans: When two bodies at different temperatures \[{{\mathbf{T}}_{\mathbf{1}}}\] and \[{{\mathbf{T}}_{\mathbf{2}}}\] are in thermal contact. They do not always settle at their mean temperature because the thermal capacities of two bodies may not always be equal.

7. The resistance of certain platinum resistance thermometer is found to be \[2.56\text{ }\Omega \] at ${{0}^{\circ }}C$ and \[3.56\text{ }\Omega \] at \[{{1000}^{\circ }}C\]. When the thermometer is immersed in a given liquid, its resistance is observed to \[5.06\text{ }\Omega \]. Determine the temperature of liquid?

Ans: In the above question it is given that:

\[{{R}_{o}}\text{ }=\text{ }Resistance\]at  ${{0}^{\circ }}C=2.56\Omega $ 

\[{{R}_{t}}\text{ }=\text{ }Resistance\text{ }at\text{ }temperature\text{ }T\text{ }=\text{ }{{1000}^{\circ }}\text{C is 3}.56\text{ }\Omega \]

\[{{R}_{t}}\text{ }=\text{ }Resistance\text{ }at\text{ }unknown\text{ }temperature\text{ }t\];

\[{{R}_{t\text{ }}}=\text{ }5.06\Omega \]

As $t=\frac{{{R}_{t}}-{{R}_{0}}}{{{R}_{100}}-{{R}_{0}}}\times 100$

$\Rightarrow t=\frac{5.06-2.56}{3.56-2.56}\times 100={{250}^{\circ }}C$

8. A ball is dropped on a floor from a height of 2cm. After the collision, it rises up to a height of 1.5m. Assuming that 40% of mechanical energy lost goes to thermal energy into the ball. Calculate the rise in temperature of the ball in the collision. Specific heat capacity of the ball is 800J/k. Take \[g\text{ }=\text{ }10m/{{s}^{2}}\].

Ans: In the above question it is given that:

\[Initial\text{ }height\text{ }=\text{ }{{h}_{1}}=2m\]

\[Final\text{ }height\text{ }=\text{ }{{h}_{2}}=1.5m\]

\[Since\text{ }potential\text{ }energy\text{ }=\text{ }mechanical\text{ }energy\text{ }for\text{ }a\text{ }body\text{ }at\text{ }rest\text{ }as\text{ }K.E\text{ }=0\]

\[Mechanical\text{ }energy\text{ }lost\text{ }=\left| mg\left( {{h}_{1}}-{{h}_{2}} \right) \right|\]

$=\left| 1\times 10\left( 105-2 \right) \right|=5J$

Now \[\left( mechanical\text{ }energy\text{ }lost \right)\text{ }\times \text{ }40%\text{ }=\text{ }heat\text{ }gained\text{ }by\text{ }ball\]

$\frac{40}{100}\times 5=Cm\Delta T$

$\Rightarrow \frac{40}{100}\times 5=800\times 1\times \Delta T$

Therefore, 

\[\Delta T=\frac{100\times 800}{40\times 5}=2.5\times {{10}^{-3}}{{\text{ }}^{o}}C\], which is the required rise in temperature.

9. A thermometer has wrong calibration. It reads the melting point of ice as \[\text{ }\mathbf{1}{{\mathbf{0}}^{\mathbf{0}}}\mathbf{C}\]. It reads \[\mathbf{6}{{\mathbf{0}}^{\mathbf{0}}}\mathbf{C}\] in place of \[\mathbf{5}{{\mathbf{0}}^{\mathbf{0}}}\mathbf{C}\]. What is the temperature of boiling point of water on the scale?

Ans: In the above question it is given that:

Lower fixed point on the wrong scale is \[\text{ }\mathbf{1}{{\mathbf{0}}^{\mathbf{0}}}\mathbf{C}\].

Let \[n\text{ }=\text{ }no.\text{ }divisions\text{ }between\text{ }upper\text{ }and\text{ }lower\text{ }fixed\text{ }points\text{ }on\text{ }this\text{ }scale\]. 

If \[Q\text{ }=\text{ }reading\text{ }on\text{ }this\text{ }scale\], then

$\frac{C-0}{100}=\frac{Q-\left( -10 \right)}{n}$

Now, \[C\text{ }=\text{ }Incorrect\text{ }Reading\text{ }=\text{ }{{60}^{0}}C\]

\[Q\text{ }=\text{ }Correct\text{ }Reading\text{ }=\text{ }{{50}^{0}}C\]

So, 

$\frac{50-0}{100}=\frac{60-\left( -10 \right)}{n}$

$\frac{50}{100}=\frac{70}{n}$

\[n\text{ }=\text{ }140\]

Now,

$\frac{C-0}{100}=\frac{Q-\left( -10 \right)}{n}$

On the Celsius scale, Boiling point of water is \[{{100}^{0}}C\]

So,

$\frac{100-0}{100}=\frac{Q+10}{140}$

\[Q\text{ }=\text{ }{{130}^{0}}C\], which is the temperature of boiling point of water on this scale.

10. Write the advantages and disadvantages of platinum resistance thermometer.

Ans: Advantages of Platinum Resistance thermometer are as follows:

1. High accuracy of measurement

2. Measurements of temperature can be made over a wide range of temperature i.e., from \[{{260}^{0}}C\text{ }to\text{ }{{1200}^{0}}C\].

      Disadvantages of Platinum Resistance thermometer are as follows:

1. High Cost

2. Requires additional equipment such as bridge circuit, Power supply etc.

11. If the volume of block of metal changes by 0.12% when it is heated through 200C. What is the co-efficient of linear expansion of the metal?

Ans:  The co-efficient of cubical expansion y of the metal is given by:

$Y=\frac{1}{V}\times \frac{\Delta V}{\Delta T}$

$\Rightarrow Y=\frac{\Delta V}{V}\times \frac{1}{\Delta T}$

Here, $\frac{\Delta V}{V}=\frac{0.12}{100}$

$\Delta T={{20}^{0}}C$

$Y=\frac{0.12}{100}\times \frac{1}{20}$

$\Rightarrow Y=6\times {{10}^{-5}}{{/}^{0}}C$

$\therefore$ Co-efficient of linear expansion of the metal is:

$\alpha =\frac{Y}{3}=\frac{6\times {{10}^{-5}}}{3}=2\times {{10}^{-5}}{{/}^{0}}C$

12. The density of a solid at00C and 5000C is in the ratio 1.027: 1. Find the co-efficient of linear expansion of the solid?

Ans: In the above question it is given that:

\[Density\text{ }at\text{ }{{0}^{0}}C\text{ }=\text{ }{{S}_{O}}\]

\[Density\text{ }at\text{ }{{500}^{0}}C\text{ }=\text{ }{{S}_{500}}\]

Now, \[{{S}_{O}}\text{ }=\text{ }{{S}_{500}}\left( 1+Y\Delta T \right)\]

Where, \[Y\text{ }=\text{ }Co-efficient\text{ }of\text{ }volume\text{ }expansion\]

\[\Delta T\text{ }=\text{ }Change\text{ }in\text{ }temperature\]

$\frac{{{S}_{O}}}{{{S}_{500}}}=\frac{1.027}{1}$

\[\Delta T\text{ }=\text{ }Change\text{ }in\text{ }temperature\]

\[\Delta T\text{ }=\text{ }Final\text{ }Temperature\text{ }\text{ }Initial\text{ }temperature\]

\[\Delta T\text{ }=\text{ }500\text{ }-\text{ }{{0}^{0}}C\]

\[\Delta T\text{ }=\text{ }{{500}^{0}}C\]

Or $1.027=1\times \left( 1+Y\Delta T \right)$

$1.027=1+Y\Delta T$

$\Rightarrow 1.027-1=Y\Delta T$

$\Rightarrow 0.027=Y\Delta T$

$\Rightarrow \frac{0.027}{500}=Y$

$\Rightarrow Y=54\times {{10}^{-5}}{{/}^{0}}C$

Now, the co-efficient of linear expansion \[\left( \alpha  \right)\] is related to co-efficient of volume expansion (Y) as:

\[\alpha =\frac{Y}{3}=\frac{54\times {{10}^{-5}}}{3}=18\times {{10}^{-5}}{{/}^{0}}C\]

13. If one Mole of a monatomic gas is mixed with 3 moles of a diatomic gas. What is the molecular specific heat of the mixture at constant volume?

Ans: We know that:

For, a monatomic gas, \[Specific\text{ }heat\text{ }at\text{ }consent\text{ }volume\text{ }=\text{ }{{C}_{V1}}\text{ }=\frac{3}{2}R\] ; 

\[R\text{ }=\text{ }Universal\text{ }Gas\text{ }Constant\]

\[No.\text{ }of\text{ }moles\text{ }of\text{ }monatomic\text{ }gas\text{ }=\text{ }{{n}_{1}}\text{ }=\text{ }1\text{ }mole\]

\[No.\text{ }of\text{ }moles\text{ }of\text{ }diatomic\text{ }gas\text{ }=\text{ }{{n}_{2}}\text{ }=\text{ }3\text{ }moles\].

For, diatomic gas, specific heat at constant volume, \[{{C}_{V2}}\text{ }=\frac{5}{2}R\]

Applying, conservation of energy.

Let \[{{C}_{V}}\text{ }=\text{ }Specific\text{ }heat\text{ }of\text{ }the\text{ }mixture\];

${{C}_{V}}=\frac{{{n}_{1}}{{C}_{{{v}_{1}}}}+{{n}_{2}}{{C}_{{{n}_{2}}}}}{{{n}_{1}}+{{n}_{2}}}$

$\Rightarrow {{C}_{V}}=\frac{1\times \frac{3}{2}R+3\times \frac{5}{2}R}{1+3}$

$\Rightarrow {{C}_{V}}=\frac{\frac{3}{2}R+\frac{15}{2}R}{4}$

R = Universal Gas constant

$\Rightarrow {{C}_{V}}=\frac{9R}{4}=\frac{9\times 8.31}{4}=18.7J/mol/K$

14. Calculate the difference between two principal specific heats of 1g of helium gas at N. T. P. Given Molecular weight of Helium = 4 and J = 4.186 J/cal and Universal Gas constant, R = 8.314J / mole / K?

Ans: We know that:

\[Molecular\text{ }weight\text{ }of\text{ }Helium\text{ }=\text{ }M\text{ }=\text{ }4\]

\[Universal\text{ }Gas\text{ }Constant,\text{ }R\text{ }=\text{ }8.31J/mole/K\]

\[{{C}_{P}}\text{ }=\text{ }specific\text{ }heat\text{ }at\text{ }constant\text{ }Pressure\]

\[{{C}_{V}}\text{ }=\text{ }specific\text{ }heat\text{ }at\text{ }constant\text{ }Volume\]

Now, ${{C}_{P}}-{{C}_{V}}=\frac{r}{J}$ for 1 mole of gas.

${{C}_{P}}-{{C}_{V}}=\frac{R}{MJ}$

Where, \[R\text{ }=\text{ }Universal\text{ }Gas\text{ }Constant\text{ }=\text{ }8.31J/mole/K\] 

\[J\text{ }=\text{ }4.186\text{ }J/cal\]

\[M\text{ }=\text{ }Molecular\text{ }weight\text{ }of\text{ }Helium\text{ }=\text{ }4\]

$\Rightarrow {{C}_{P}}-{{C}_{V}}=\frac{8.31}{4\times 4.186}$

$\Rightarrow {{C}_{P}}-{{C}_{V}}=0.496cal/g/K$, which is the required difference.

15. Why does heat flow from a body at higher temperature to a body at lower temperature?

Ans: If a body at a higher temperature is in contact with a body at a lower temperature, molecules with a more kinetic energy that are in contact with less energetic molecules give some of their kinetic energy to the less energetic ones.

16. A one litre flask contains some mercury. IT is found that at different temperatures, then volume of air inside the flask remains the same. What is the volume of mercury in the flask? Given the co-efficient of linear expansion of glass \[=\text{ }9\text{ }\times \text{ }{{10}^{-6}}\text{ }/{{\text{ }}^{0}}C\] and co- efficient of volume expansion of mercury \[=\text{ }1.8\text{ }\times \text{ }{{10}^{-4}}\text{ }/{{\text{ }}^{0}}C\].

Ans: It is given that the volume of air in the flask remains the same at different temperatures. This is possible only when the expansion of glass is exactly equal to the expansion of mercury, Co-efficient of cubical expansion of glass is:-

${{\gamma }_{g}}=3{{\alpha }_{g}}=3\times 9\times {{10}^{-5}}=27\times {{10}^{-5}}{{/}^{0}}C$

The co-efficient of cubical expansion of mercury is:

${{\gamma }_{m}}=1.8\times {{10}^{-4}}{{/}^{0}}C$

Volume of flask, \[V\text{ }=\text{ }1\text{ }liter\text{ }=\text{ }1000\text{ }c{{m}^{3}}\].

Let \[{{V}_{m}}\text{ c}{{m}^{3}}\] be the volume of mercury in the flask.

\[Expansion\text{ }of\text{ }flask\text{ }=\text{ }Expansion\text{ }of\text{ }Mercury\]

$C\times {{\gamma }_{g}}\times t={{V}_{m}}\times {{\gamma }_{m}}\times t$

∴ Volume of Mercury, ${{V}_{m}}=\frac{V\times {{\gamma }_{g}}}{{{\gamma }_{m}}}$

$\Rightarrow {{V}_{m}}=\frac{1000\times 27\times {{10}^{-5}}}{1.8\times {{10}^{-4}}}=150c{{m}^{3}}$

17. The potential energy function for a particle executing linear simple harmonic motion is given by \[\mathbf{V}\left( \mathbf{x} \right)\text{ }=k{{x}^{2}}/\mathbf{2}\], where k is the force constant of the oscillator. For k = 0.5 N/m, the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must 'turn back' when it reaches x = ± 2 m.

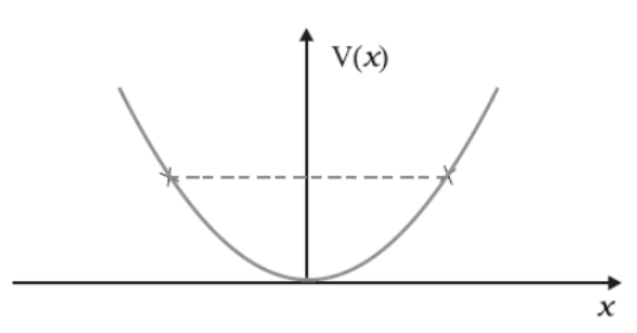
Ans: In the above question it is given that:

Total energy of the particle, \[E=\text{ }1J\].

Force constant, \[k=\text{ }0.5\text{ }N/m\].

Kinetic energy of the particle, \[K\text{ }=\frac{1}{2}m{{v}^{2}}\]

According to the conservation law:

\[E=\text{ }V\text{ }+\text{ }K\]

\[1=\text{ }\frac{1}{2}k{{x}^{2}}\text{ }+\text{ }\frac{1}{2}m{{v}^{2}}\]

At the moment of ‘turn back', velocity (and hence K) becomes zero.

$\therefore 1=\frac{1}{2}k{{x}^{2}}$

$\frac{1}{2}\times 0.5{{x}^{2}}=1$

${{x}^{2}}=4$

$x=\pm 2$

Thus, the particle turns back when it reaches $x=\pm 2$m.

18. State if each of the following statements is true or false. Give reasons for your Answer.

1. In an elastic collision of two bodies, the momentum and energy of each body is conserved.

Ans: The above statement is false. This is because in an elastic collision, the total energy and momentum of both the bodies, and not of each individual body, is conserved.

2. Total energy of a system is always conserved, no matter what internal and external forces on the body are present.

Ans: The above statement is false. This is because although internal forces are balanced, they cause no work to be done on a body. It is the external forces that have the ability to do work. Hence, external forces are able to change the energy of a system.

3. Work done in the motion of a body over a closed loop is zero for every force in nature.

Ans: The above statement is false. This is because the work done in the motion of a body over a closed loop is zero for a conservation force only.

4. In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.

Ans: The above statement is true. This is because in an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system. This is because in such collisions, there is always a loss of energy in the form of heat, sound, etc.

19. A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to

(i) ${{t}^{\frac{1}{2}}}$ 

(ii) t  

(iii) \[{{t}^{\frac{3}{2}}}\] 

(iv) ${{t}^{2}}$

Ans: The power delivered to it at time t is proportional to t i.e., option (ii) t is the correct choice.

\[Mass\text{ }of\text{ }the\text{ }body\text{ }=\text{ }m\]

\[Acceleration\text{ }of\text{ }the\text{ }body\text{ }=\text{ }a\]

Using Newton's second law of motion, the force experienced by the body is given by: \[F\text{ }=\text{ }ma\].

Both m and a are constants. Hence, force F will also be a constant.

\[F\text{ }=\text{ }ma\text{ }=\text{ }Constant\] ..... (i)

For velocity v, acceleration is given as,

$a=\frac{dv}{dt}=c\text{onstant}$

$dv=c\text{onstant}\times \text{dt}$

$v=\alpha t$ …… (ii)

Where, $\alpha $ is another constant.

$v\propto t$ …… (iii)

Power is given by the relation:

\[P\text{ }=\text{ }F.v\]

Using equations (i) and (iii), we have:

$P\propto t$

Hence, power is directly proportional to time.

20. A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to

(i) ${{t}^{\frac{1}{2}}}$ 

(ii) t  

(iii) \[{{t}^{\frac{3}{2}}}\] 

(iv) ${{t}^{2}}$

Ans: Its displacement in time t is proportional to \[{{t}^{\frac{3}{2}}}\], $\therefore$ option (iii) is the right answer.

Power is given by the relation:

\[P\text{ }=\text{ }F.v\]

$=mav=mv\frac{dv}{dt}=\text{constant=k}$

$\Rightarrow vdv=\frac{k}{m}dt$

Integrating both sides:

$\frac{{{v}^{2}}}{2}=\frac{k}{m}t$

$v=\sqrt{\frac{2kt}{m}}$

For displacement of the body, we have:

$v=\frac{dx}{dt}=\sqrt{\frac{2k}{m}}{{t}^{\frac{1}{2}}}$

$dx=k'{{t}^{\frac{1}{2}}}dt$

Where $k'=\sqrt{\frac{2k}{3}}=$ New constant

On integrating both sides, we get:

$x=\frac{2}{3}k'{{t}^{\frac{3}{2}}}$

$\Rightarrow x\propto {{t}^{\frac{3}{2}}}$, which is the required proportionality.

21. A pump on the ground floor of a building can pump up water to fill a tank of volume $30{{m}^{3}}$ in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?

Ans: In the above question it is given that:

Volume of the tank, $V=30{{m}^{3}}$.

Time of operation, \[t=\text{ }15\text{ }min\text{ }=\text{ }15\text{ }\times 60\text{ }=\text{ }900\text{ }s\].

Height of the tank, \[h=\text{ }40\text{ }m\].

Efficiency of the pump, \[\eta =\text{ }30%\]

Density of water, $\rho ={{10}^{3}}kg/{{m}^{3}}$

Mass of water, \[m=\rho V=30\times {{10}^{3}}kg\]

Output power can be obtained as:

${{P}_{0}}=\frac{Wo\text{rk d}one}{Time}=\frac{mgh}{t}$

$\frac{30\times {{10}^{3}}\times 9.8\times 40}{900}=13.067\times {{10}^{3}}W$

For input power, efficiency is given by the relation:

$\eta =\frac{{{P}_{0}}}{{{P}_{1}}}=30%$

$\Rightarrow {{P}_{1}}=\frac{13.067}{30}\times 100\times {{10}^{3}}$

$\Rightarrow {{P}_{1}}=43.6kW$, which is the required power consumption.

22. A body of mass 0.5 kg travels in a straight line with velocity $v=a{{x}^{\frac{3}{2}}}$ where $a=5m/{{s}^{2}}$. What is the work done by the net force during its displacement from x = 0 to x = 2 m?

Ans: In the above question it is given that:

Mass of the body, \[m=\text{ }0.5\text{ }kg\].

Velocity of the body is governed by the equation,

$v=a{{x}^{\frac{3}{2}}}$ where $a=5m/{{s}^{2}}$.

Initial velocity, \[u\text{ }\left( at\text{ }x\text{ }=\text{ }0 \right)\text{ }=\text{ }0\]

Final velocity \[v\text{ }\left( at\text{ }x\text{ }=\text{ }2\text{ }m \right)=10\sqrt{2}m/s\]

Work done, \[W\text{ }=\text{ }Change\text{ }in\text{ }kinetic\text{ }energy\]

$=\frac{1}{2}m\left( {{v}^{2}}-{{u}^{2}} \right)$

$=\frac{1}{2}\times 0.5\times \left( {{\left( 10\sqrt{2} \right)}^{2}}-0 \right)$

$=50J$

23. A family uses 8 kW of power. 

1. Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW? 

Ans: In the above question it is given that:

Power used by the family, \[P\text{ }=\text{ }8\text{ }kW\text{ }=\text{ 8}\times {{10}^{3}}W\]

Solar energy received per square metre \[=\text{ }200\text{ }W\]

Efficiency of conversion from solar to electricity energy \[=\text{ }20\text{ }%\]

Area required to generate the desired electricity \[=\text{ }A\]

As per the information given in the question, 

\[\text{8}\times {{10}^{3}}=20%\times \left( A\times 200 \right)\]$=\frac{20}{100}\times A\times 200$

$\Rightarrow A=200{{m}^{2}}$

2. Compare this area to that of the roof of a typical house.

Ans: The area of a solar plate required to generate \[8\text{ }kW\] of electricity is almost equivalent to the area of the roof of a building having dimensions \[14\text{ }m\times 14\text{ }m\].

24. A bolt of mass 0.3 kg falls from the ceiling of an elevator moving down with a uniform speed of 7m/s. It hits the floor of the elevator (length of the elevator = 3 m) and does not rebound. What is the heat produced by the impact? Would your answer be different if the elevator were stationary?

Ans: In the above question it is given that:

Mass of the bolt, \[m=\text{ }0.3\text{ }kg\].

\[Speed\text{ }of\text{ }the\text{ }elevator\text{ }=\text{ }7\text{ }m/s\].

Height, \[h\text{ }=\text{ }3\text{ }m\].

As the relative velocity of the bolt with respect to the lift is zero, at the time of impact, potential energy gets converted into heat energy.

\[Heat\text{ }produced\text{ }=\text{ }Loss\text{ }of\text{ }potential\text{ }energy\text{ }=\text{ }mgh\text{ }=\text{ }=\text{ }8.82\text{ }J\]

The heat produced will remain the same even if the lift is stationary. This is due to the fact that the relative velocity of the bolt with respect to the lift will remain zero.

25. Consider the decay of a free neutron at rest: \[n\text{ }\to \text{ }p+\text{ }e-\]. Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the $\beta $ decay of a neutron or a nucleus (Fig. 6.19).

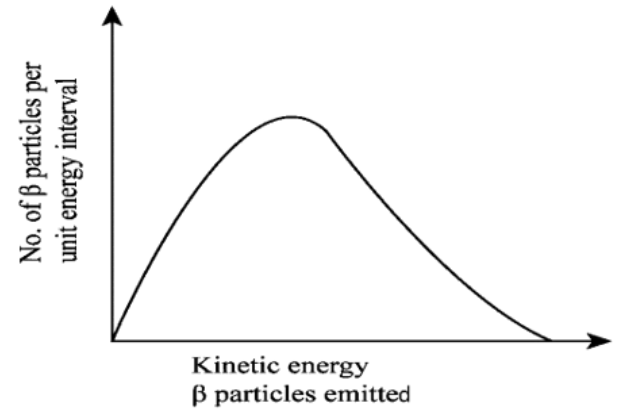
(Note: The simple result of this exercise was one among the several arguments advanced by W. Pauli to predict the existence of a third particle in the decay products of $\beta $ decay. This particle is known as neutrino. We now know that it is a particle of intrinsic spin 1/2 (like e-, p or n), but is neutral, and either massless or having an extremely small mass (compared to the mass of electron) and which interacts very weakly with matter. The correct decay process of neutron is: \[n\text{ }\to \text{ }p+\text{ }e-\])

Ans: The decay process of free neutron at rest is \[n\text{ }\to \text{ }p+\text{ }e-\].

Using Einstein's mass-energy relation, we have the energy of electron as $\Delta m{{c}^{2}}$.

Where,

\[\Delta m=\text{ }Mass\text{ }defect\text{ }=\text{ }Mass\text{ }of\text{ }neutron-\left( Mass\text{ }of\text{ }proton\text{ }+\text{ }Mass\text{ }of\text{ }electron \right)\]

\[c\text{ }=\text{ }Speed\text{ }of\text{ }light\]

\[\Delta m\] and c are constants. Thus, the given two-body decay is unable to explain the continuous energy distribution in the $\beta $ decay of a neutron or a nucleus. The presence of neutrino on the LHS of the decay correctly interprets the continuous energy distribution.

Long Answer Questions                                                                                   3 Marks

1. Prove that in an elastic collision in one dimension the relative velocity of approach before impact is equal to the relative velocity of separation after impact.

Ans: Consider the figure given below:

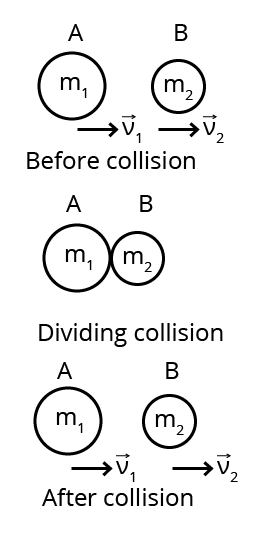
According to law of conservation of linear momentum

${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$

\[{{m}_{1}}\left( {{u}_{1}}-{{v}_{1}} \right)={{m}_{2}}\left( {{v}_{2}}-{{u}_{2}} \right)\] …… (1)

K.E. also remains conserved.

$\frac{1}{2}{{m}_{1}}{{u}_{1}}^{2}+\frac{1}{2}{{m}_{2}}{{u}_{2}}^{2}=\frac{1}{2}{{m}_{1}}{{v}_{1}}^{2}+\frac{1}{2}{{m}_{2}}{{v}_{2}}^{2}$

${{m}_{1}}\left( {{u}_{1}}^{2}-{{v}_{1}}^{2} \right)={{m}_{2}}\left( {{v}_{2}}^{2}-{{u}_{2}}^{2} \right)$ …… (2)

Dividing (2) by (1)

${{u}_{1}}-{{v}_{1}}={{v}_{2}}+{{u}_{2}}$

${{u}_{1}}-{{u}_{2}}={{v}_{2}}-{{v}_{1}}$

i.e., \[Relative\text{ }velocity\text{ }of\text{ }approach\text{ }=\text{ }Relative\text{ }velocity\text{ }of\text{ }separation\].

2. Calculate \[{{C}_{p}}\] for air, given that \[{{C}_{v}}\text{ }=0.162\text{ }cal\text{ }{{g}^{-1}}\text{ }{{k}^{-1}}\] and density air at N.T. P is \[0.001293\text{ }g/c{{m}^{3}}\].

Ans: In the above question it is given that:

\[Specific\text{ }heat\text{ }at\text{ }constant\text{ }volume\text{ }=\text{ }{{C}_{v\text{ }}}=\text{ }0.162\text{ }Cal\text{ }{{g}^{-1\text{ }}}{{k}^{-1}}\]

Specific heat at constant pressure = \[{{C}_{p}}=\text{ }?\]

Now, \[{{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{r}{J}=\frac{PV}{TJ}\left( \because PV=nRT \right)\]

\[{{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{P\times 1}{s\times TJ}\left( s=Density \right)\]

\[\Rightarrow {{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{1.01\times {{10}^{5}}}{273\times 4.2\times {{10}^{7}}\times 1.293\times {{10}^{-3}}}\]

\[\Rightarrow {{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{1.01\times {{10}^{6+3-7}}}{273\times 4.2\times {{10}^{7}}\times 1.293}\]

\[\Rightarrow {{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{1.01\times {{10}^{2}}}{1482.5}=6.8\times {{10}^{-2}}\]

\[\Rightarrow {{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=0.068\]

\[\Rightarrow {{C}_{p}}\text{ }=\text{ }0.162+0.068\]

\[\Rightarrow {{C}_{p}}\text{ }=\text{ }0.23\text{ c}al\text{ }{{g}^{-1}}\text{ }{{k}^{-1}}\], which is the required value asked to determine.

3. Develop a relation between the co-efficient of linear expansion, co-efficient superficial expansion and coefficient of cubical expansion of a solid.

Ans: As the \[co-efficient\text{ }of\text{ }linear\text{ }expansion\text{ }=\text{ }\alpha \text{ }=\frac{\Delta L}{L\Delta T}\]

Where,

\[\Delta L\text{ }=\text{ }change\text{ }in\text{ }length\]

\[L\text{ }=\text{ }length\]

\[\Delta T\text{ }=\text{ }change\text{ }in\text{ }temperature\].

In the same way,

\[Co-efficient\text{ }of\text{ }superficial\text{ }expansion\text{ }=\text{ }\beta \text{ }=\frac{\Delta S}{S\Delta T}\]

\[\Delta S\text{ }=\text{ }change\text{ }in\text{ }area\]

\[S\text{ }=\text{ }original\text{ }area\]

\[\Delta T\text{ }=\text{ }change\text{ }in\text{ }temperature\]

Co-efficient of cubical expansion, \[Y\text{ }=\frac{\Delta V}{V\Delta T}\]

\[\Delta V\text{ }=\text{ }change\text{ }in\text{ }volume\]

\[V\text{ }=\text{ }original\text{ }volume\]

\[\Delta T\text{ }=\text{ }change\text{ }in\text{ }temperature\].

Now, 

\[\Delta L=\alpha L\text{ }\Delta T\]

\[\Rightarrow L\text{ }+\text{ }\Delta L\text{ }=\text{ }L\text{ }+\text{ }\alpha L\text{ }\Delta T\]

\[\Rightarrow L\text{ }+\text{ }\Delta L\text{ }=\text{ }L\text{ }\left( 1+\alpha \Delta T \right)\] …… (1)

Similarly,

\[V+\text{ }\Delta V\text{ }=\text{ }V\text{ }\left( 1+Y\Delta T \right)\] ……. (2)

And 

\[S+\Delta S=S\text{ }\left( 1+\beta \Delta T \right)\] …… (3)

Also, 

\[\left( V+\Delta V \right)\text{ }=\text{ }{{\left( L+\Delta L \right)}^{3}}\]

\[\Rightarrow V+\Delta V={{L}^{3}}\left( 1+3\alpha \Delta T+3{{\alpha }^{2}}\Delta {{T}^{2}}+{{\alpha }^{3}}{{T}^{3}} \right)\]

Since \[{{\alpha }^{2}},\text{ }{{\alpha }^{3}}\] are negligible, so,

\[V+\gamma \text{ }V\Delta T=\text{ }V\left( 1+3\alpha \Delta T \right)\] \[\left[ as\text{ }{{L}^{3\text{ }}}=\text{ }V \right]\]

So, 

\[V+\gamma V\Delta T\text{ }=\text{ }V+V3\alpha \Delta T\]

\[\Rightarrow \gamma V\Delta T\text{ }=\text{ }3\alpha \Delta T\]

\[\Rightarrow \gamma \text{ }=\text{ }3\alpha \]

Similarly, \[\beta \text{ }=\text{ }2\alpha \] (using \[{{L}^{2}}\text{ }=\text{ }S\text{ }\left( Area \right)\])

So,

\[\alpha =\frac{\beta }{2}=\frac{\gamma }{3}\], which is the required relation.

4. Calculate the amount of heat required to convert 1.00kg of ice at \[\text{ }\mathbf{1}{{\mathbf{0}}^{\mathbf{0}}}C\] into steam at \[\mathbf{10}{{\mathbf{0}}^{\mathbf{0}}}C\] at normal pressure. Specific heat of ice = 2100J/kg/k. Latent heat of fusion of ice = 3.36x105 J/kg, specific heat of water = 4200J/kg/k. Latent heat of vaporization of water \[=\text{ }2.25\times {{10}^{6}}J/kg\].

Ans: In the above question it is given that:

Heat is required to raise the temperature of ice from \[\text{ }{{10}^{0}}C\text{ }to\text{ }{{0}^{0}}C.\]

Thus, change in temperature \[=\text{ }\Delta T\text{ }=\text{ }T2-T1\text{ }=\text{ }0-\left( -10 \right)\text{ }=\text{ }{{10}^{0}}C\].

So, \[\Delta Q1=cm\Delta T\]

\[C\text{ }=\text{ }specific\text{ }heat\text{ }of\text{ }ice\]

\[M\text{ }=\text{ }Mass\text{ }of\text{ }ice\]

\[\Delta T\text{ }=\text{ }{{10}^{0}}C\]

\[\Delta {{Q}_{1}}\text{ }=\text{ }2100\times 1\times 10=21000J\]

(2) Heat required to melt the ice to \[{{0}^{0}}C\] water:

\[\Delta {{Q}_{2}}=\text{ }mL\]

\[L\text{ }=\text{ }Latent\text{ }heat\text{ }of\text{ }fusion\text{ }of\text{ }ice\text{ }=\text{ }3.36\times 105\text{ }J/kg\]

\[m\text{ }=\text{ }Mass\text{ }of\text{ }ice\]

\[\Rightarrow \Delta {{Q}_{2}}=1\times 3.36\times 105\text{ }J/kg\]

\[\Rightarrow \Delta {{Q}_{2}}=3.36\times 105\text{ }J\]

\[\Rightarrow \Delta {{Q}_{2}}=336000J\]

(3) Heat required to raise the temperature of water from \[{{0}^{0}}C\] to \[{{100}^{0}}C\]:-

\[\Delta T\text{ }=\text{ }T2-T1\text{ }=\text{ }100-0={{100}^{0}}C\]

\[\Delta {{Q}_{3}}=\text{ }cm\Delta Tc\text{ }=\text{ }specific\text{ }heat\text{ }of\text{ }water\]

\[\Rightarrow \Delta {{Q}_{3}}=4200\times 1\times 100\]

\[\Rightarrow \Delta {{Q}_{3}}=420,000J\]

(4) Heat required to convert 1000C water to steam at 1000C

\[\Delta {{Q}_{4}}=\text{ }mL\]

Where, \[L\text{ }=\text{ }Latent\text{ }heat\text{ }of\text{ }vapourisation\text{ }=\text{ }2.25\times {{10}^{6}}J/kg\]

\[\Rightarrow \Delta {{Q}_{4}}=\text{ }1\times 2.25\times 106J/kg\]

\[\Rightarrow \Delta {{Q}_{4}}=2250000J\]

\[Total\text{ }Heat\text{ }required\text{ }=\Delta {{Q}_{1}}+\Delta {{Q}_{2}}+\Delta {{Q}_{3}}+\Delta {{Q}_{4}}\]

\[\Rightarrow \Delta {{Q}_{total}}=\text{ }21000+336000+420000+2250000\]

\[\Rightarrow \Delta {{Q}_{total}}=\text{ }3027000J\]

\[\Rightarrow \Delta {{Q}_{total}}=\text{ }3.027\times {{10}^{6}}J\]

5. The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:

1. Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.

Ans: The sign of work done is positive. In the given case, force and displacement are in the same direction. Hence, the sign of work done is positive. In this case, the work is done on the bucket.

2. Work done by gravitational force in the above case,

Ans: The sign of work done is negative. In the given case, the direction of force (vertically downward) and displacement (vertically upward) are opposite to each other. Hence, the sign of work done is negative.

3. Work done by friction on a body sliding down an inclined plane,

Ans: The sign of work done is negative. Since the direction of frictional force is opposite to the direction of motion, the work done by the frictional force is negative in this case.

4. Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,

Ans: The sign of work done is positive. Here the body is moving on a rough horizontal plane. Frictional force opposes the motion of the body. Therefore, in order to maintain a uniform velocity, a uniform force must be applied to the body. Since the applied force acts in the direction of motion of the body, the work done is positive.

5. Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.

Ans: The sign of work done is negative. The resistive force of air acts in the direction opposite to the direction of motion of the pendulum. Hence, the work done is negative in this case.

6. Choose the correct alternative:

1. When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.

Ans: Decreases, this is because:

A conservative force does a positive work on a body when it displaces the body in the direction of force. As a result, the body advances toward the centre of force. It decreases the separation between the two, thereby decreasing the potential energy of the body. 

2. Work done by a body against friction always results in a loss of its kinetic/potential energy.

Ans: Kinetic energy, this is because:

The work done against the direction of friction reduces the velocity of a body. Hence, there is a loss of kinetic energy of the body.

3. The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.

Ans: External force, this is because:

Internal forces, irrespective of their direction, cannot produce any change in the total momentum of a body. Hence, the total momentum of a many- particle system is proportional to the external forces acting on the system.

4. In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.

Ans: Total linear momentum, this is because:

The total linear momentum always remains conserved whether it is an elastic collision or an inelastic collision.

7. Answer carefully, with reasons:

1. In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e., when they are in contact)

Ans: No. This is because in an elastic collision, the total initial kinetic energy of the balls will be equal to the total final kinetic energy of the balls. This kinetic energy is not conserved at the instant the two balls are in contact with each other. In fact, at the time of collision, the kinetic energy of the balls will get converted into potential energy.

2. Is the total linear momentum conserved during the short time of an elastic collision of two balls?

Ans: Yes. This is because in an elastic collision, the total linear momentum of the system always remains conserved.

3. What are the answers to (a) and (b) for an inelastic collision?

Ans: No; Yes. This is because in an inelastic collision, there is always a loss of kinetic energy, i.e., the total kinetic energy of the billiard balls before collision will always be greater than that after collision. The total linear momentum of the system of billiards balls will remain conserved even in the case of an inelastic collision.

4. If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).

Ans: Elastic. This is because in the given case, the forces involved are conservation. This is because they depend on the separation between the centres of the billiard balls. Hence, the collision is elastic.

8. A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated. 

1. How much work does she do against the gravitational force?

Ans: In the above question it is given that:

Mass of the weight, \[m\text{ }=\text{ }10\text{ }kg\].

Height to which the person lifts the weight, \[h\text{ }=\text{ }0.5\text{ }m\].

Number of times the weight is lifted, \[n\text{ }=\text{ }1000\]

$\therefore$ Work done against gravitational force is:

$=nmgh$

$=1000\times 10\times 9.8\times 0.5$

$=49kJ$

2. Fat supplies J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?

Ans: We know that:

\[Energy\text{ }equivalent\text{ }of\text{ }1\text{ }kg\text{ }of\text{ }fat\text{ }=\text{ 3}\text{.8}\times \text{1}{{\text{0}}^{7}}J\]

\[Efficiency\text{ }rate\text{ }=\text{ }20%\]

Mechanical energy supplied by the person's body will be:

$=\frac{20}{100}\times 3.8\times {{10}^{7}}$

$=\frac{1}{5}\times 3.8\times {{10}^{7}}$

Equivalent mass of fat lost by the dieter will be:

$=\frac{1}{\frac{1}{5}\times 3.8\times {{10}^{7}}}\times 49\times {{10}^{3}}$

$=6.45\times {{10}^{-3}}kg$

Long Answer Questions                                                                                  4 Marks

1. A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1.

Compute the following:

(a) Work done by the applied force in 10 s,

(b) Work done by friction in 10 s,

(c) Work done by the net force on the body in 10 s,

(d) Change in kinetic energy of the body in 10 s, and interpret your results.

Ans: In the above question it is given that:

Mass of the body, \[m=\text{ }2\text{ }kg\].

Applied force, \[F\text{ }=\text{ }7\text{ }N\].

Coefficient of kinetic friction, \[\mu =\text{ }0.1\]

Initial velocity, \[u=\text{ }0\]

Time, \[t\text{ }=\text{ }10\text{ }s\].

The acceleration produced in the body by the applied force is given by Newton's second law of motion as:

$a'=\frac{F}{m}=\frac{7}{2}=3.5m/{{s}^{2}}$

Frictional force is given as:

$f=\mu mg=0.1\times 2\times 9.8=-1.96N$

The acceleration produced by the frictional force:

$a''=-\frac{1.96}{2}=0.98m/{{s}^{2}}$

Total acceleration of the body:

$a=a'+a''=3.5-0.98=2.52m/{{s}^{2}}$

The distance travelled by the body is given by the equation of motion:

$s=ut+\frac{1}{2}a{{t}^{2}}$$=0+\frac{1}{2}\times 2.52\times {{10}^{2}}=126m$

Thus,

1. Work done by the applied force, ${{W}_{s}}=F\times s=7\times 126=882J$

2. Work done by the frictional force, ${{W}_{f}}=F\times s=-1.96\times 126=-247J$

3. Net force \[~=7-1.96=\text{ }5.04\text{ }N\] 

Work done by the net force, \[{{W}_{net}}=\text{ }5.04\text{ }\times 126\text{ }=\text{ }635\text{ }J\].

4. From the first equation of motion, final velocity can be calculated as:

$v=u+at$$=0+2.52\times 10=25.2m/s$

Change in kinetic energy 

$=\frac{1}{2}m{{v}^{2}}-\frac{1}{2}m{{u}^{2}}$

$=\frac{1}{2} 2\left ( v^{2}-u^{2} \right)=\left ( -25.2 \right )^{2}-0^{2}=635 J$

2. A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4 relative to the trolley in a direction opposite to its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?

Ans: In the above question it is given that:

Mass of the trolley, \[M=\text{ }200\text{ }kg\].

Speed of the trolley, \[v=\text{ }36\text{ }km/h\text{ }=\text{ }10\text{ }m/s\].

Mass of the boy, \[m=\text{ }20\text{ }kg\].

Initial momentum of the system of the boy and the trolley

\[=\text{ }\left( M+\text{ }m \right)v\]

$=\left( 200+20 \right)\times 10$

\[=\text{ }2200\text{ }kg\text{ }m/s\]

Let v' be the final velocity of the trolley with respect to the ground.

Final velocity of the boy with respect to the ground $=v'-4$

Final momentum $=Mv'+m\left( v'-4 \right)$

$=200v'+20v'-80$

$=220v'-80$

As per the law of conservation of momentum:

\[Initial\text{ }momentum\text{ }=\text{ }Final\text{ }momentum\]

\[2200\text{ }=220v'-80\]

$\Rightarrow v'=\frac{2280}{220}=10.36m/s$

Length of the trolley, \[l=\text{ }10\text{ }m\].

Speed of the boy, \[v''\text{ }=\text{ }4\text{ }m/s\].

Time taken by the boy to run, $t=\frac{10}{4}=2.5s$.

Thus, the distance moved by the trolley $=v''\times t=10.36\times 2.5=25.9m$.

3. A 1 kg block situated on a rough incline is connected to a spring of spring constant 100 N/m as shown in Fig. 6.17. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.

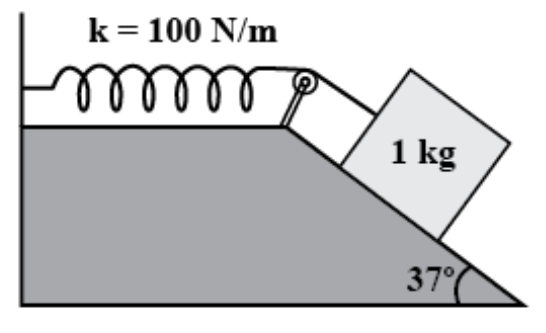
Ans: In the above question it is given that:

Mass of the block, \[m=\text{ }1\text{ }kg\]

Spring constant, \[k=100N/m\]

Displacement in the block, \[x=\text{ }10\text{ }cm\text{ }=\text{ }0.1\text{ }m\]

The given situation can be shown as in the following figure.

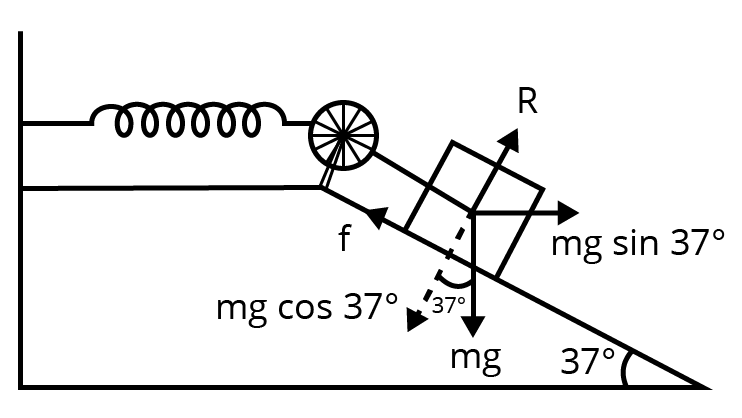
At equilibrium:

Normal reaction, \[R=\text{ }mg\text{ }cos\text{ }37{}^\circ \]

Frictional force, \[f\text{ = }\mu R\text{ }=\text{ }mg\text{ }sin\text{ }37{}^\circ \]

Where, \[\mu \] is the coefficient of friction.

Net force acting on the block \[=mg\sin {{37}^{0}}-f\]

\[=mg\sin {{37}^{0}}-\mu mgco\operatorname{s}{{37}^{0}}\]

\[=mg\left( \sin {{37}^{0}}-\mu co\operatorname{s}{{37}^{0}} \right)\]

At equilibrium, the work done by the block is equal to the potential energy of the spring, i.e.,

\[mg\left( \sin {{37}^{0}}-\mu mgco\operatorname{s}{{37}^{0}} \right)x=\frac{1}{2}k{{x}^{2}}\]

\[\Rightarrow 1\times 9.8\left( \sin {{37}^{0}}-\mu mgco\operatorname{s}{{37}^{0}} \right)x=\frac{1}{2}100\times {{0.1}^{2}}\]

$\Rightarrow 0.602-\mu \times 0.799=0.510$

$\Rightarrow \mu =\frac{0.092}{0.799}=0.115$, which is the required coefficient of friction.

4. Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

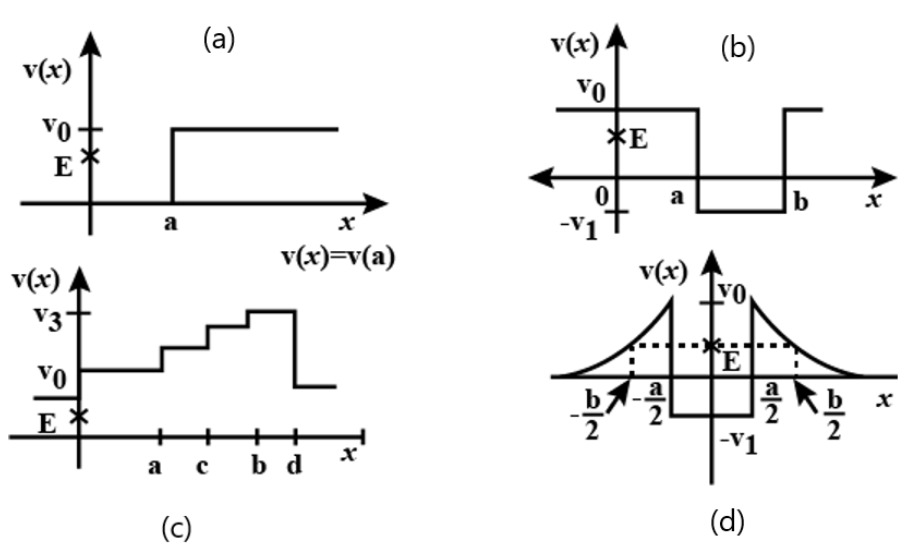
Ans: 

1. From the given figure: \[x\text{ }>\text{ }a;\text{ 0}\]

Total energy of a system is:\[E\text{ }=\text{ }P.E.\text{ }+\text{ }K.\text{ }E.\]

The kinetic energy of a body is a positive quantity. It cannot be negative. Therefore, the particle will not exist in a region where K.E. becomes negative. In this case, the potential energy $\left( {{V}_{0}} \right)$ of the particle becomes greater than total energy (E)  for \[x\text{ }>\text{ }a\]. Hence, kinetic energy becomes negative in this region. Therefore, the particle will not exist in this region. The minimum total energy of the particle is zero.

2. From the given figure, all the regions the particle cannot be found for the given energy. In the given case, the potential energy (PE) is greater than total energy (E) in all regions. Hence, the particle will not exist in this region.

3. From the given figure: $x>a$ and \[x\text{ }<\text{ }b;-{{V}_{1}}\]

In the given case, the condition regarding the positivity of K.E. is satisfied only in the region between $x>a$ and \[x\text{ }<\text{ }b\].The minimum potential energy in this case is \[{{V}_{1}}\]. Therefore, 

\[KE=\text{ }E-\left( -{{V}_{1}} \right)=E+{{V}_{1}}\].

Therefore, for the positivity of the kinetic energy, the total energy of the particle must be greater than \[{{V}_{1}}\]. So, the minimum total energy the particle must have is \[{{V}_{1}}\].

4. From the given figure: $-\frac{b}{2}<x<\frac{a}{2};-\frac{a}{2}<x<\frac{a}{2};-{{V}_{1}}$

In the given case, the potential energy \[\left( \text{ }{{\text{V}}_{0}} \right)\] of the particle becomes greater than the total energy (E) for $-\frac{b}{2}<x<\frac{a}{2}$ and $-\frac{a}{2}<x<\frac{a}{2}$. Therefore, the particle will not exist in these regions.

The minimum potential energy in this case is $-{{V}_{1}}$. Therefore,\[KE=\text{ }E-\left( -{{V}_{1}} \right)=E+{{V}_{1}}\].

Therefore, for the positivity of the kinetic energy, the total energy of the particle must be greater than $-{{V}_{1}}$. So, the minimum total energy the particle must have is $-{{V}_{1}}$.

5. An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton? Obtain the ratio of their speeds. 

(electron mass \[=9.11\times {{10}^{-31}}\text{ }kg\], proton mass \[=1.67\times {{10}^{-27}}\text{ }kg\], \[1\text{ }eV\text{ }=\text{ 1}\text{.60}\times \text{1}{{\text{0}}^{-19}}J\]).

Ans: In the above question it is given that:

Mass of the electron \[=9.11\times {{10}^{-31}}\text{ }kg\]

Mass of the proton \[=1.67\times {{10}^{-27}}\text{ }kg\]

Kinetic energy of the electron, \[{{E}_{Ke}}=\text{ }10\text{ }keV\text{ }=\text{ 1}{{\text{0}}^{4}}eV\]

\[=\text{1}{{\text{0}}^{4}}\times \text{1}\text{.60}\times \text{1}{{\text{0}}^{-19}}\text{=1}\text{.60}\times \text{1}{{\text{0}}^{-15}}J\]

Kinetic energy of the proton, ${{E}_{Kp}}=100keV={{10}^{5}}eV=1.60\times {{10}^{-14}}J$.

For the velocity of an electron ${{v}_{e}}$, its kinetic energy is given by the relation:

${{E}_{Ke}}=\frac{1}{2}m{{v}_{e}}^{2}$

$\Rightarrow {{v}_{e}}=\sqrt{\frac{2\times {{E}_{Ke}}}{m}}$$=\sqrt{\frac{2\times 1.60\times {{10}^{-15}}}{9.11\times {{10}^{-31}}}}=5.93\times {{10}^{7}}m/s$

For the velocity of a proton ${{v}_{p}}$, its kinetic energy is given by the relation:

${{E}_{Kp}}=\frac{1}{2}m{{v}_{p}}^{2}$

$\Rightarrow {{v}_{p}}=\sqrt{\frac{2\times {{E}_{Kp}}}{m}}$$=\sqrt{\frac{2\times 1.60\times {{10}^{-15}}}{1.67\times {{10}^{-27}}}}=4.38\times {{10}^{6}}m/s$

Hence, the electron is moving faster than the proton.

The ratio of their speeds:

$\frac{{{v}_{e}}}{{{v}_{p}}}=\frac{5.93\times {{10}^{7}}}{4.38\times {{10}^{6}}}=13.54:1$

It is clear that electrons are faster; Ratio of speeds is \[13.54:\text{ }1\].

6. The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?

Ans: In the above question it is given that:

Length of the pendulum, \[l\text{ }=\text{ }1.5\text{ }m\]

Mass of the bob \[=\text{ }m\]

Energy dissipated \[=\text{ }5%\]

Using the law of conservation of energy, the total energy of the system remains constant.

At the horizontal position:

Potential energy of the bob, \[EP\text{ }=\text{ }mgl\]

Kinetic energy of the bob, \[EK\text{ }=\text{ }0\]

\[Total\text{ }energy\text{ }=\text{ }mgl\] ... (i)

At the lowermost point (mean position):

Potential energy of the bob, \[EP\text{ }=\text{ }0\]

Kinetic energy of the bob, ${{E}_{k}}=\frac{1}{2}m{{v}^{2}}$.

Total energy, ${{E}_{k}}=\frac{1}{2}m{{v}^{2}}$... (ii)

As the bob moves from the horizontal position to the lowermost point, 5% of its energy gets dissipated. The total energy at the lowermost point is equal to 95% of the total energy at the horizontal point, i.e., 

$\frac{1}{2}m{{v}^{2}}=\frac{95}{100}\times mgl$

$\Rightarrow v=\sqrt{\frac{2\times 95\times 1.5\times 9.8}{100}}=528m/s$, which is the required speed.

7. The blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t? (b) What is the kinetic energy of the air? (c) Assume that the windmill converts 25% of the wind's energy into electrical energy, and that A = $30{{m}^{2}}$ , v = 36 km/h and the density of air is \[\mathbf{1}.\mathbf{2}\text{ }\mathbf{kg}/{{m}^{3}}\]. What is the electrical power produced?

Ans: In the above question it is given that:

\[Area\text{ }of\text{ }the\text{ }circle\text{ }swept\text{ }by\text{ }the\text{ }windmill\text{ }=\text{ }A\]

\[Velocity\text{ }of\text{ }the\text{ }wind\text{ }=\text{ }v\]

\[Density\text{ }of\text{ }air\text{ }=\rho \]

1. Volume of the wind flowing through the windmill per sec \[=\text{ }Av\]

Mass of the wind flowing through the windmill per sec \[=\text{ }\rho Av\]. Mass m, of the wind flowing through the windmill in time \[t=\rho Avt\]

2. Kinetic energy of air $=\frac{1}{2}m{{v}^{2}}=\frac{1}{2}\left( \rho Avt \right){{v}^{2}}=\frac{1}{2}\rho A{{v}^{3}}t$

3. Area of the circle swept by the windmill \[=\text{ }A\text{ }=\text{ }30\text{ }{{m}^{2}}\]

Velocity of the wind \[=\text{ }v=\text{ }36\text{ }km/h\]

Density of air, $\rho =1.2kg/{{m}^{3}}$

\[Electric\text{ }energy\text{ }produced\text{ }=\text{ }25%\text{ }of\text{ }the\text{ }wind\text{ }energy\]

$=\frac{25}{100}\times Kinet\text{ic energy of a}ir$

$=\frac{1}{8}\rho A{{v}^{3}}t$

Also,

\[Electrical\text{ }power=\frac{Electrica\text{l e}nergy}{Time}\]

$=\frac{1}{8}\frac{\rho A{{v}^{3}}t}{t}=\frac{1}{8}\rho A{{v}^{3}}$

$=\frac{1}{8}\times 1.2\times 30\times {{10}^{3}}=4.5kW$

5 Marks Questions

1. 

1. Define potential energy. Give examples.

Ans: Potential energy is defined as the energy possessed by a body by virtue of its position in a field or due to change in its configuration example – A gas compressed in a cylinder, A wound spring of a water, water raised to the overhead tank in a house etc.

2. Draw a graph showing the variation of potential energy, kinetic energy and the total energy of a body freely falling on earth from a height h?

Ans: The graph below shows the variation of potential energy, kinetic energy and the total energy of a body freely falling on earth from a height h:

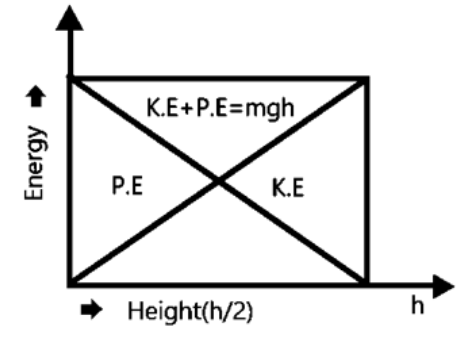
(i) Gravitational potential energy decreases as the body falls downwards and is zero at the earth

(ii) Kinetic energy increases as the body falls downwards and is maximum when the body just strikes the ground.

(iii) According to the law of conservation of energy, total mechanical (KE + PE) energy remains constant.

2. Answer the following:

1. The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?

Ans: At rocket’s expense the heat energy required for burning is obtained. The burning of the casing of a rocket in flight (due to friction) results in the reduction of the mass of the rocket. According to the conservation of energy:

\[Total\text{ }Energy\left( T.E. \right)=\text{ }Potential\text{ }enegry\left( P.E. \right)+Kinetic\text{ }energy\left( K.E. \right)\]

$mgh+\frac{1}{2}m{{v}^{2}}$

The reduction in the rocket's mass causes a drop in the total energy. Therefore, the heat energy required for the burning is obtained from the rocket.

2. Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet's velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?

Ans: Gravitational force is a conservative force. As the work done by a conservative force over a closed path is zero, the work done by the gravitational force over every complete orbit of a comet is zero.

3. An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?

Ans: When an artificial satellite, orbiting around earth, moves closer to earth, its potential energy decreases due to the reduction in the height. As the total energy of the system remains constant, the reduction in P.E. results in an increase in K.E. Hence, the velocity of the satellite increases. However, due to atmospheric friction, the total energy of the satellite decreases by a small amount.

4. In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?

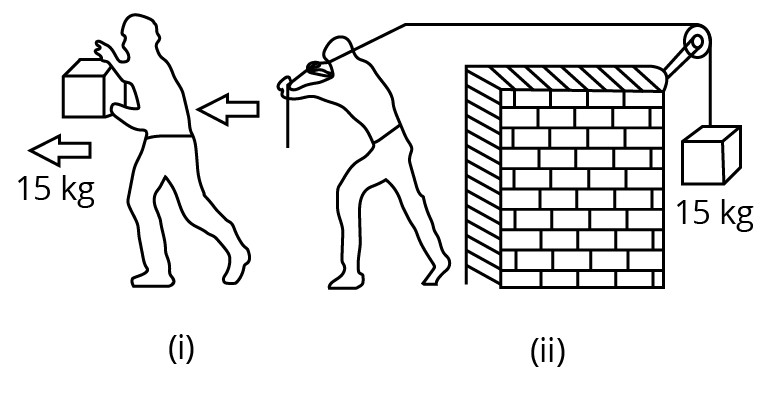
Ans: In the second case, the work done is greater.

Case (i):

Mass, \[m\text{ }=\text{ }15\text{ }kg\]

Displacement, \[s\text{ }=\text{ }2\text{ }m\]

Work done, \[W=Fs\cos \theta \]

Where, \[\theta =Angle\text{ }between\text{ }force\text{ }and\text{ }displacement\]

\[W=mgs\cos \theta =15\times 2\times 9.8\cos {{90}^{0}}=0\]

Case (ii):

Mass, \[m\text{ }=\text{ }15\text{ }kg\]

Displacement, \[s\text{ }=\text{ }2\text{ }m\]

Here, the direction of the force applied on the rope and the direction of the displacement of the rope are the same.

Therefore, the angle between them, $\theta ={{0}^{0}}$

As, $\cos {{0}^{0}}=1$ 

Work done, \[W={{F}_{s}}\cos \theta =mgs\]$=15\times 9.8\times 2=294J$

Thus, work done in the second case is greater.

3. A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is $10m/s$?

Ans: In the above question it is given that:

Radius of the rain drop, \[r=\text{ }2\text{ }mm\text{ }=\text{ 2}\times {{10}^{-3}}m\].

Volume of the rain drop, \[V=\frac{4}{3}\pi {{r}^{3}}\]

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}kg\]

Density of water, $\rho ={{10}^{3}}kg/{{m}^{3}}$

Mass of the rain drop, \[m=\rho V\]

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}kg\]

Gravitational force, \[F\text{ }=\text{ }mg\]

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}\times 9.8N\]

The work done by the gravitational force on the drop in the first half of its journey:

${{W}_{1}}=Fs$

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}\times 9.8\times 250\]

\[=\text{ }0.082\text{ }J\]

This amount of work is equal to the work done by the gravitational force on the drop in the second half of its journey, i.e., \[{{W}_{II}}=\text{ }0.082\text{ }J\]As per the law of conservation of energy, if no resistive force is present, then the total energy of the rain drop will remain the same.

Total energy at the top will be:

${{E}_{T}}=mgh+0$

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}\times 9.8\times 500\times {{10}^{-5}}\]

$=0.164J$

Due to the presence of a resistive force, the drop hits the ground with a velocity of 10 m/s.

Total energy at the ground will be:

${{E}_{G}}=\frac{1}{2}m=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}\times 9.8\times {{10}^{2}}$

$=1.675\times {{10}^{-3}}J$

Clearly,

\[Work\text{ }done\text{ }by\text{ }resistive\text{ }force\text{ }={{E}_{G}}-{{E}_{T}}=-0.162J\]

4. Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figures is a possible result after collision?

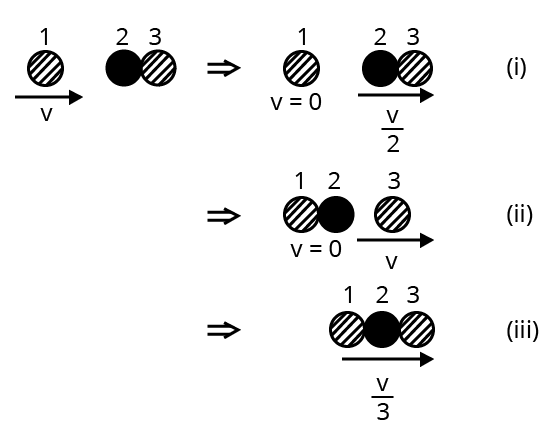
Ans: 

Case (i) result is possible after a collision

It is observed that the total momentum before and after collision in each case is constant. For an elastic collision, the total kinetic energy of a system remains conserved before and after the collision. For the mass of each ball bearing m, 

The total kinetic energy of the system before collision:

$=\frac{1}{2}m{{v}^{2}}-\frac{1}{2}\left( 2m \right)0$

$=\frac{1}{2}m{{v}^{2}}$

Case (ii):Total kinetic energy of the system after collision:

$=\frac{1}{2}\left( m \right)0+\frac{1}{2}\left( 2m \right){{\left( \frac{v}{2} \right)}^{2}}$

$=\frac{1}{4}m{{v}^{2}}$

Hence, the kinetic energy of the system is not conserved in case (i).

Case (iii):Total kinetic energy of the system after collision: 

$=\frac{1}{2}\left( 2m \right)0+\frac{1}{2}m{{v}^{2}}$

$=\frac{1}{2}m{{v}^{2}}$

Thus, the kinetic energy of the system is conserved in case (ii).

Case (vi):Total kinetic energy of the system after collision:

$=\frac{1}{2}\left( 3m \right){{\left( \frac{v}{3} \right)}^{2}}$

$=\frac{1}{6}m{{v}^{2}}$

Thus, the kinetic energy of the system is not conserved in case (iii).

5. A bullet of mass 0.012 kg and horizontal speed of $70m/s$ strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.

Ans: In the above question it is given that:

Mass of the bullet, \[m=\text{ }0.012\text{ }kg\]

Initial speed of the bullet, \[{{u}_{b}}=\text{ }70\text{ }m/s\].

Mass of the wooden block, \[M=\text{ }0.4\text{ }kg\]

Initial speed of the wooden block, \[{{u}_{g}}=\text{ }0\]

Final speed of the system of the bullet and the block \[=\text{ }v\]

Applying the law of conservation of momentum:

$m{{u}_{b}}+M{{u}_{g}}=\left( m+M \right)v$

$0.012\times 70+0.4\times 0=\left( 0.012+0.4 \right)v$

$\Rightarrow v=\frac{0.84}{0.412}=2.041m/s$

For the system of the bullet and the wooden block:

Mass of the system, \[m'\text{ }=\text{ }0.412\text{ }kg\]

Velocity of the system \[=\text{ }2.04\text{ }m/s\]

Height up to which the system rises \[=\text{ }h\]

Applying the law of conservation of energy to this system:

\[Potential\text{ }energy\text{ }at\text{ }the\text{ }highest\text{ }point\text{ }=\text{ }Kinetic\text{ }energy\text{ }at\text{ }the\text{ }lowest\text{ }point\]

$m'gh=\frac{1}{2}m'{{v}^{2}}$

$\Rightarrow h=\frac{1}{2}\left( \frac{{{v}^{2}}}{g} \right)$$=\frac{1}{2}\times \frac{{{\left( 2.04 \right)}^{2}}}{9.8}$$=0.2123m$

The wooden block will rise to a height of \[0.2123\text{ }m\].

\[Heat\text{ }produced\text{ }=\text{ }Kinetic\text{ }energy\text{ }of\text{ }the\text{ }bullet\text{ }-\text{ }Kinetic\text{ }energy\text{ }of\text{ }the\text{ }system\]

$\Rightarrow \frac{1}{2}m{{u}^{2}}-\frac{1}{2}m'{{v}^{2}}$\[=\frac{1}{2}\times 0.012\times {{70}^{2}}-\frac{1}{2}\times 0.412\times {{2.04}^{2}}=28.54J\]

6. Two inclined frictionless tracks, one gradual and the other steep, meet at A from where two stones are allowed to slide down from rest, one on each track (Fig. 6.16). Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain. Given \[{{\theta }_{1}}=\text{ }30{}^\circ ,\text{ }{{\theta }_{2}}=\text{ }60{}^\circ ,\]and h = 10 m, what are the speeds and times taken by the two stones?

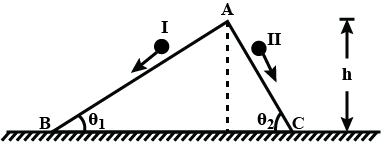
Ans: No, they won’t reach there with the same speed.

The stone moving down the steep plane will reach the bottom first.

Yes; the stones will reach the bottom with the same speed

\[{{v}_{b}}={{v}_{c}}=\text{ }14\text{ }m/s\]

\[{{t}_{1}}=\text{ }2.86\text{ }s;\text{ }{{\text{t}}_{2}}=\text{ }1.65\text{ }s\]

The given situation can be shown as in the following figure:

Here, the initial height (AD) for both stones is the same (h). Hence, both will have the same potential energy at point A.

As per the law of conservation of energy, the kinetic energy of the stones at points B and C will also be the same, i.e.,

$\frac{1}{2}m{{v}_{1}}^{2}=\frac{1}{2}m{{v}_{2}}^{2}$

Consider, ${{v}_{1}}={{v}_{2}}=v$

Where,

\[m\text{ }=\text{ }Mass\text{ }of\text{ }each\text{ }stone\]

\[v=\text{ }Speed\text{ }of\text{ }each\text{ }stone\text{ }at\text{ }points\text{ }B\text{ }and\text{ }C\]

Hence, both stones will reach the bottom with the same speed, v.

For stone I:

Net force acting on this stone is given by:

${{F}_{net}}=m{{a}_{1}}=mg\sin {{\theta }_{1}}$

$\Rightarrow {{a}_{1}}=g\sin {{\theta }_{1}}$

For stone II:

${{a}_{2}}=g\sin {{\theta }_{2}}$

$\Rightarrow {{\theta }_{2}}>{{\theta }_{1}}$

$\Rightarrow {{a}_{2}}>{{a}_{1}}$

Using the first equation of motion, the time of slide can be obtained as:

$v=u+at$

$\Rightarrow t=\frac{v}{a}\left( \because u=0 \right)$

For stone I:

${{t}_{1}}=\frac{v}{{{a}_{1}}}$

For stone II:

${{t}_{2}}=\frac{v}{{{a}_{2}}}$

$\Rightarrow {{a}_{2}}>{{a}_{1}}$

$\Rightarrow {{t}_{2}}<{{t}_{1}}$

Thus, the stone moving down the steep plane will reach the bottom first.

The speed (v) of each stone at points B and C is given by the relation obtained from the law of conservation of energy.

$mgh=\frac{1}{2}m{{v}^{2}}$

$\Rightarrow v=\sqrt{2gh}=\sqrt{2\times 9.8\times 10}=14m/s$

Thus,

${{t}_{1}}=\frac{v}{{{a}_{1}}}=\frac{v}{g\sin {{\theta }_{1}}}=\frac{14}{9.8\times \sin {{30}^{0}}}=2.86s$

And

${{t}_{2}}=\frac{v}{{{a}_{2}}}=\frac{v}{g\sin {{\theta }_{2}}}=\frac{14}{9.8\times \sin {{60}^{0}}}=1.65s$, which are the corresponding times taken by both the stones.

Important Questions from Work, Energy and Power (Short, Long & Practice)

Short Answer Type Questions

1. A spring is stretched. Is the work done by the stretching force positive or negative?

2. What is the work done by the centripetal force? Why?

3. What is the work done by the tension in the string of a simple pendulum?

Long Answer Type Questions

1. Prove that instantaneous power is given, by the dot product of force and velocity i.e. P = F.v.

2. State and prove work-energy theorem or principle.

3. State and prove the law of conservation of energy.

4. A 10 kg block slides without acceleration down a rough inclined plane making an angle of 20° with the horizontal. Calculate the work done over a distance of 1.2 m when the inclination of the plane is increased to 30°.

Practice Questions

1. A bullet of mass 20 g moving with a velocity of 500 ms-1 strikes a tree and goes out from the other end. with a velocity of 400 ms-1. Calculate the work done in passing through the tree.

2. A stone of mass 5 kg falls from the top of a cliff 30 m high and buries itself one metre deep into the sand. Find the average resistance offered and time taken to penetrate into the sand.

3. A wooden ball is dropped from a height of 2 m. What is the height up to which the ball will rebound if the coefficient of restitution is 0.5?

Download Important Questions For Class 11 Physics Chapter 5

Chapter 5 of Class 11 Physics Work, Power, and Energy is an important topic to be covered by the students for securing good scores in the Board exams as well as in the competitive exams. Students find Chapter 5 Work, Power, and Energy as one of the difficult topics to be covered in Physics, but students will be able to tackle this by practising more and more questions with the help of work energy and power Class 11 important questions with answers Pdf available on the Vedantu platform. Class 11 Physics Chapter 5 Important Questions Pdf is prepared for students in such a way that they will be able to solve the questions effortlessly.

Work Energy And Power Class 11 Important Questions With Answers

Students must be familiar with Chapter 5 Work, Power, and Energy for attempting Class 11 Physics Chapter 5 Important Questions. The chapter includes interesting topics like a work-energy theorem, kinetic energy, potential energy, conservation of energy, power, collisions, etc… 

Students must be well versed with Chapter 5 for appearing in the CBSE board exams. The most common difficulty encountered by the students is how to approach the question. The approach of the question is understood by practising questions from related topics. Before starting with the practice of Class 11 Physics work energy and power important questions students should have a brief revision of the chapter which is available on the Vedantu website.

Physics Chapter 5 - Work, Energy, and Power

In NCERT Physics syllabus Work, Energy, and Power chapter is of high importance from an examination point of view. Students must be familiar with the terms of work, energy, and power from their elementary classes. In our everyday life, we use these terms so casually but the Physics behind them is interesting. In order to have a hold on any subject, it is only possible with regular studies and practice. Work, Energy, and Power is a chapter that can be understood with real-life exams. Work energy and power Class 11 important questions with answers covered all the questions with suitable examples students can relate it to quickly. 

Students should start studying by questioning, for example, now we are on Chapter 5 Work, Energy, and Power. The very first question that arises in a student's mind is what is work. Work and energy are two terms that we come across most often, work and energy are interrelated concepts. For solving important questions from work energy and power Class 11, students should understand the complete chapter and remember a few topics such as :

• Work: Work is just energy transferred by force.

• Work Done: Work done is defined as when an external force acts upon a body in steady motion; it will experience some displacement; this action is termed as the work is done.

• Energy: The ability to do work is known as energy. There are several types of energy like electrical energy, solar energy, mechanical energy, etc. In this chapter, we will focus mainly on mechanical energy and its types. There are basically two types of mechanical energy:

1. Kinetic Energy: The energy gained by an object due to its motion is known as the kinetic energy of that object.

2. Potential Energy: The energy gained by an object due to its position is known as the potential energy of that object.

• Power: The rate of doing work is known as power.

• Work Energy Theorem: Work energy theorem states that work done by the external forces on an object is equal to the change in its kinetic energy.

• Conservation of Energy: Conservation of energy can be stated as- energy is a conserved quantity it can neither be created nor be destroyed.

Like these, there are many more interesting concepts included in Chapter 5 of Class 11 Physics. Not only these we will also come across topics like momentum, conservation of momentum, collisions, type of collision, etc… There are high chances of getting numerical type problems in competitive exams from this chapter. Not only numerical type questions we also get to see questions that demand for graphical methods, derivations, and multiple choices type questions. 

The work, energy, and power chapter compiled of many more important topics that can be mastered by practicing Class 11 Physics Chapter 5 Important Questions. The work, Energy and Power chapter mainly focus on bringing the idea of how work is defined, the difference between work and work done, Mechanical energy and its types, etc…  Refer to the material available on the Vedantu for a detailed explanation.

Chapter 5 of Class 11 Physics syllabus as prescribed by CBSE, NCERT board have numerous topics, derivations, diagrams, graphs. Students must focus on derivation parts carefully with clear understanding.  Numerical problems, MCQs, Revision notes of Chapter 5 are available on the Vedantu website and they are prepared by experts after deep research and analysis of CBSE, NEET, JEE exam papers and students find them reliable. Before starting with the preparation of the exams, students should go through the chapters thoroughly without skipping any topic as in Physics every topic will be related to another topic.

Key Features of Important Questions for Class 11 Physics Chapter 5 - Work, Energy and Power

• Important Questions are curated in the right manner to help students in quickly finding solutions.

• Step-by-step explanations for all questions from previous years are included.

• All solutions are easy to understand as they are solved by subject experts to match the syllabus.

• These Important Questions on Work, Energy and Power help students in developing strong conceptual foundations for students, which is important in the final stages of preparation for board and competitive exams.

• These Important Questions are available in PDF format and can be downloaded for free.

Conclusion

Important Questions on Class 11 Physics Work, Energy and Power are a very important material for students preparing for Class XI Examination as well as competitive exams. From the discussion above, students will get an idea about the type of questions in the final examination. Students can rely on these Important Questions as they are curated by experts.

Important Related Links for CBSE Class 11