Important Questions for CBSE Class 11 Physics Chapter 11 - Thermodynamics

1 Marks Questions

1. If an air is a cylinder is suddenly compressed by a piston. What happens to the pressure of air?

Ans: If the piston suddenly compresses then it causes heating and rise in temperature and if the piston is maintained at same Position, then the pressure falls as temperature decreases.

2. What is the ratio of find volume to initial volume if the gas is compressed adiabatically till its temperature is doubled?

Ans: We know that for an adiabatic Process,

${\text{P}}{{\text{V}}^{\text{Y}}} = $ constant

Since, ${\text{PV}} = {\text{RT}}$

${\text{P}} = \dfrac{{RT}}{V}$

So, $\dfrac{{{\text{RT}}{{\text{V}}_Y}}}{{\text{V}}} = {\text{constant}}$

Or $T{V_{{\text{y}} - 1}}$ = constant ${{\text{T}}_1},\;{{\text{V}}_1} = $ Initial temperature and Initial Volume

$\therefore {{\text{T}}_1}\;{{\text{V}}_1}_{\text{y}} - 1 = {{\text{T}}_2}\;{{\text{V}}_{2Y - 1}}{{\text{T}}_2},\;{{\text{V}}_2} = $ Final temperature and Final volume.

$\dfrac{{{V_2}}}{{{V_1}}} = {\left( {\dfrac{{{T_1}}}{{{T_2}}}} \right)^{\dfrac{1}{{1 - 1}}}}$

Since ${{\text{T}}_2} = 2\;{{\text{T}}_1}$ (Given)

$\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{1}{2}$

So, $\dfrac{{{V_2}}}{{{V_1}}} = {\left( {\dfrac{1}{2}} \right)^{\dfrac{1}{{\bar I - 1}}}}$

Since $\dfrac{4}{Y} > 1,\dfrac{{{V_2}}}{{{V_1}}}$ is less than $\dfrac{1}{2}$.

3. What is the ratio of slopes of P-V graphs of adiabatic and isothermal process?

Ans: Let, the slope of P-V graph is $\dfrac{{dP}}{{dV}}$

We know that for an isothermal process, (PV = constant)

So, $\dfrac{{dP}}{{dV}} = \dfrac{P}{V} \to (1)$

For an adiabatic process ( ${\text{P}}{{\text{V}}^{\text{Y}}} = $ constant)

$\dfrac{{{\text{dP}}}}{{{\text{dV}}}} = \dfrac{{{\text{YP}}}}{{\text{V}}} \to (2)$

Divide 2) by 1)

So, the ratio of adiabatic slope to isothermal slope is ${\text{Y}}$.

4. What is the foundation of Thermodynamics?

Ans: The law of conservation of energy and the observation that heat travels from a hot body to a cool body are the foundations of thermodynamics.

5. Differentiate between isothermal and adiabatic process?

Ans: The difference between Isothermal and Adiabatic process is given below:

6. A Carnot engine develops 100 H.P. and operates between ${27^0}{\text{C}}$ and ${227^0}{\text{C}}$. Find:

1. Thermal efficiency

Ans: Here, energy $ = {\text{W}} = 100{\text{H}}.{\text{P}}$.

$ = 100 \times 746\;{\text{W}}$ ( $1{\text{H}}.{{\text{P}}_.} = 746\;{\text{W}}$ )

$ = \dfrac{{(100 \times 746)}}{{4.2}}{\text{cal}}\mid {\text{s}}\left( {1\;{\text{W}} = \dfrac{{{\text{cal}}\mid {\text{s}}}}{{4.2}}} \right)$

High temperature, ${{\text{T}}_{\text{H}}} = {227^0}{\text{C}} = 227 + 273 = 500\;{\text{K}}$

Low temperature, ${{\text{T}}_{\text{h}}} = {27^0}{\text{C}} = 27 + 273 = 300\;{\text{K}}$

Thermal efficiency, $\eta  = 1 - \dfrac{{{T_L}}}{{{T_H}}}$ $\eta  = 1 - \dfrac{{300}}{{500}}$

$\eta  = \dfrac{{200}}{{500}} = 0.4$ or $40\% $

2. Heat supplied

Ans: The heat supplied ${{\text{Q}}_{\text{H}}}$ is given by: -

${Q_H} = \dfrac{W}{\eta } = \dfrac{{100 \times 746}}{{4.2 \times 0.4}} = 4.44 \times {10^4}{\text{cal/s}}$

3. Heat rejected

Ans: The heat rejected ${{\text{Q}}_{\text{L}}}$ is given by: -

${Q_L} = {Q_H}\dfrac{{{T_L}}}{{{T_H}}}$ or $\dfrac{{{Q_L}}}{{{Q_H}}} = \dfrac{{{T_L}}}{{{T_H}}}$

${Q_L} = 4.44 \times {10^4} \times \dfrac{{3\emptyset \phi }}{{5\emptyset {\phi ^\prime }}}$

${Q_L} = 2.66 \times {10^4}{\text{cal/}}\Delta $

7. Draw a ${\mathbf{p}}$ - ${\mathbf{v}}$ diagram for isothermal and adiabatic expansion?

Ans: Diagram of P-V for isothermal and adiabatic expansion.

8. State zeroth law of thermodynamics?

Ans: According to Zeroth law, if the thermodynamic system and are each in thermal equilibrium with a third thermodynamic system C, then the system and are also in thermal equilibrium.

9. Can a gas be liquefied at any temperature by increase of pressure alone?

Ans: No, only when the temperature of the gas is below its critical point can it be liquefied by pressure alone.

10. Can you design heat energy of $100\% $ efficiency?

Ans: Since, efficiency of heat engine $ = 1 - \dfrac{{{T_2}}}{{{T_1}}}$, 

So, efficiency will be $100\% $ or 1 if ${{\text{T}}_2} = {\text{OK}}$ or ${{\text{T}}_1} = $

a. Since both these conditions cannot be practically attained, so heat engine cannot have $100\% $ efficiency.

11. If air is a bad conductor of heat, why do we not feel warm without clothes?

Ans: We do not feel warm without clothes because, when we are without clothes air carries away heat from our body due to convection and we feel cold.

12. A body with large reflectivity is a poor emitter why?

Ans: This is because a body with large reflectivity is a poor absorber of heat and poor absorbers are poor emitters.

13. Animal’s curl into a ball, when they feel very cold?

Ans: When animals curl, their surface area decreases, and because energy radiated varies directly with surface area, heat loss due to radiation is reduced as well.

14. Why is the energy of thermal radiation less than that of visible light?

Ans: The energy of an electromagnetic ware is given by: - ${\text{E}} = {\text{hf}}$

${\text{h}} = $ Planck's constant; ${\text{f}} = $ frequency of wave. Since the frequency of thermal radiation is less than that of visible light, the energy associated with thermal radiation is less than associated with visible light.

15. Two rods A and B are of equal length. Each rod has its ends at temperature ${{\text{T}}_1}$ and ${{\text{T}}_2}$$\left( {{{\text{T}}_1} > {{\text{T}}_2}} \right)$. What is the condition that will ensure equal rates of flow through the rods A and B?

Ans: Heat flow, ${\text{Q}} = \dfrac{{{\text{KA}}\left( {{{\text{T}}_1} - {{\text{T}}_2}} \right)}}{{\text{d}}}$

${\text{K}} = $ Thermal conductivity

${\text{A}} = $ Area

${{\text{T}}_1} = $ Temperature of hot body

${{\text{T}}_2} = $ Temperature of cold body

${\text{d}} = $ distance between hot and cold body.

$Q = $ heat flow

When the rods have the same rate of conduction,

${{\text{Q}}_1} = {{\text{Q}}_2}$

$\dfrac{{{K_1}{A_1}\left( {{T_1} - {T_2}} \right)}}{d} = \dfrac{{{K_2}{A_2}\left( {{T_1} - {T_2}} \right)}}{d}$

${{\text{K}}_1},\;{{\text{K}}_2} \to $ Thermal conductivity of first and second region

${{\text{A}}_1},\;{{\text{A}}_2} \to $ Area of first and second region

or, ${{\text{K}}_1}\;{{\text{A}}_1} = {{\text{K}}_2}\;{{\text{A}}_2}$

or $\dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{K_2}}}{{{K_1}}}$

16.A Sphere is at a temperature of $600{\text{k}}$. Its cooling rate is ${\text{R}}$ in an external environment of 200k. If temperature falls to $400{\text{k}}$. What is the cooling rate ${{\text{R}}_1}$ in terms of ${\mathbf{R}}$ ?

Ans: According to Stefan's law:

${\text{E}} = $ constant ${{\text{T}}^4}$

Also, ${{\text{R}}_1} = $ constant $\left( {{{\text{T}}_2}^4 - {{\text{T}}_1}^4} \right)$

${\text{R}} = $ constant $\left( {{{\text{T}}_3}^4 - {{\text{T}}_1}^4} \right)$

${{\text{T}}_2} = $ heat of hot junction $ = 400\;{\text{K}}$

${{\text{T}}_1} = $ heat of cold junction $ = 200\;{\text{K}}$

${{\text{T}}_3} = $ heat of hot junction $ = 600\;{\text{K}}$

${{\text{R}}_1} = $ constant $\left[ {{{(400)}^4} - {{(200)}^4}} \right]$ ……(1)

${{\text{R}}_1} = $ constant $\left[ {{{(600)}^4} - {{(200)}^4}} \right]$ …….(2)

Divide equation (1) by (2)

$\left. {\dfrac{{{R_1}}}{R} = \dfrac{{\left[ {{{(400)}^4} - {{(200)}^4}} \right]}}{{\left[ {{{(600)}^4} - {{(200)}^4}} \right.}}} \right]$

$\dfrac{{{R_1}}}{R} = \dfrac{{256 \times {{10}^8} - 16 \times {{10}^8}}}{{1296 \times {{10}^8} - 16 \times {{10}^8}}} = \dfrac{{24\phi  \times {{\not \phi }^{\not z}}}}{{128{\phi ^\prime } \times {\gamma ^7}}}$

$\dfrac{{{R_1}}}{R} = \dfrac{{24}}{{128}}$

$\dfrac{{{R_1}}}{R} = \dfrac{3}{{16}}$

Therefore, ${R_1} = \left( {\dfrac{3}{{16}}} \right)R$

17. If the temperature of the sun is doubled, the rate of energy received on each will increases by what factor?

Ans: By Stefan's law: 

Rate of energy radiated $\alpha {{\text{T}}^4}$

Where,

${\text{T}}$ = Temperature

Therefore, initial rate of energy radiated is given by:

${{\text{E}}_1} = $ constant ${{\text{T}}_1}^4$ ….(1)

Where,

${{\text{T}}_1} = $ Initial temperature

Then, the final rate of energy radiated is given by:

${{\text{E}}_2} = $ constant ${\text{T}}_2^4$ …..(2)

Where,

${{\text{T}}_2} = $ Final temperature

Now, if the temperature of the sun is doubled, we get:

${{\text{T}}_2} = 2\;{{\text{T}}_1}$

${{\text{T}}_2}^4 = {(2)^4}\;{{\text{T}}_1}^4$

${{\text{T}}_2}^4 = 16\;{{\text{T}}_1}^4$ …..(3)

Substituting equation (3) in (2), we get:

${{\text{E}}_2} = $ constant $\left( {16\;{\text{T}}_1^4} \right)$

${{\text{E}}_2} = 16$ (Constant ${{\text{T}}_1}^4$ )

${E_2} = 16{E_1}$

Therefore, If the temperature of the sun is doubled, the rate of energy received on each will increases by $16{E_1}$.

18. On a winter night, you feel warmer when clouds cover the sky than when sky is clear. Why?

Ans: We know that earth absorbs heat in day and radiates at night. When sky is covered, with clouds, the heat radiated by earth is reflected back and earth becomes warmer. But if sky is clear the heat radiated by earth escapes into space.

19. If a body is heated from ${27^0}{\text{C}}$ to ${927^0}{\text{C}}$ then what will be the ratio of energies of radiation emitted?

Ans: Since, By Stefan's law: 

${\text{E}} = $ Energy radiated

${\text{T}}$ = Temperature.

${{\text{E}}_1},\;{{\text{T}}_1} \Rightarrow $ Initial energy and temperature

${{\text{E}}_2},\;{{\text{T}}_2} \Rightarrow $ Final energy and temperature.

${{\text{T}}_1} = {27^0}{\text{C}} = 27 + 273 = 300\;{\text{K}}$

${{\text{T}}_2} = {927^0}{\text{C}} = 927 + 273\;{\text{K}} = 1200\;{\text{K}}.$

${\text{E}} = $ constant ${{\text{T}}^4}$

So, ${{\text{E}}_1} = $ constant ${{\text{T}}_1}^4$

$\dfrac{{{E_1}}}{{T_1^4}} = Constant $ …….(1)

Also, $\dfrac{{{E_2}}}{{T_2^4}} = constant$ ……(2)

Equating equation (1) & (2)

$\dfrac{{{E_1}}}{{T_1^4}} = \dfrac{{{E_2}}}{{E_2^4}}$

or $\dfrac{{{E_1}}}{{{E_2}}} = {\left( {\dfrac{{{T_1}}}{{{T_2}}}} \right)^4}$

$\dfrac{{{E_1}}}{{{E_2}}} = {\left( {\dfrac{1}{4}} \right)^4}$

$\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{1}{{256}}$

or ${{\text{E}}_1}:{{\text{E}}_2} = 1:256$

20. 2Which has a higher specific heat; water or sand?

Ans: Water has higher specific heat than sand as

$\Delta T = \dfrac{Q}{{mc}}$, where ${\text{T}} = $ Temperature, ${\text{Q}} = $ Heat, ${\text{m}} = $ Mass,

${\text{C}} = $ Specific heat; Since for water temperature increases less slowly than sand hence the result.

21. Why is latent heat of vaporization of a material greater than that of latent heat of fusion?

Ans: When a liquid turns into a gas, the volume expands dramatically, and a significant amount of work is required against the surrounding atmosphere. The heat connected with the transition from solid to gas is known as latent heat of vaporisation, and therefore the answer.

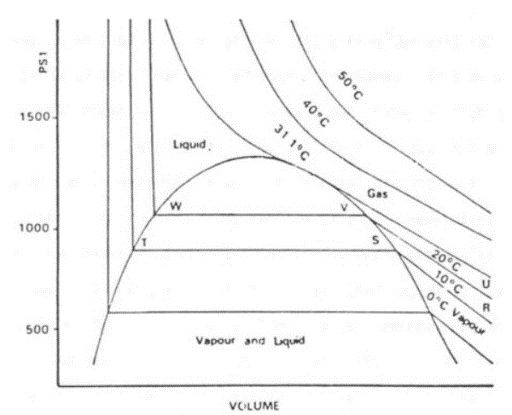
22. Draw a P - V diagram for Liquid and gas at various temperatures showing critical point?

Ans:

23. Why is temperature gradient required for flow of heat from one body to another?

Ans: Temperature gradient is required because, Heat flows from higher temperature to lower temperature. Therefore, temperature gradient (i.e., temperature difference) is required for the heat to flow one part of solid to another.

24. Why are Calorimeters made up of metal only?

Ans: Calorimeters are made of metal because metal is a good conductor of heat and thus allows for quick heat exchange, which is essential for calorimeter operation.

25. If a body has infinite heat capacity? What does it signify?

Ans: The term "infinite heat capacity" refers to a substance's ability to maintain its temperature regardless of how much heat it receives or loses.

26. Define triple point of water?

Ans: In all three states of matter, the triple point of water represents the pressure and temperature values at which water coexists in equilibrium.

27. State Dulong and petit law?

Ans: According to Dulong and petit law, the specific heat of all the solids is constant at room temperature and is equal to $3{\text{R}}$.

28. Why the clock pendulums are made of invar, a material of low value of coefficient of linear expansion?

Ans: Clock pendulums are made of invar Because, the clock pendulums are made of Inver because it has low value of a (co-efficient of linear expansion) i.e., for a small change in temperature, the length of pendulum will not change much.

29. Why does the density of solid / liquid decreases with rise in temperature?

Ans: Let The given, ${\text{P}} = $ Density of solid, liquid at temperature ${\text{T}}$

${{\text{P}}^1} = $ Density of solid, liquid at Temperature ${\text{T}} + \Delta {\text{T}}$

Since Density $ = \dfrac{{{\text{ Mass }}}}{{{\text{ Volume }}}}$

So, ${\text{P}} = \dfrac{M}{V}$ …..(1) 

${{\text{P}}^1} = \dfrac{M}{{{v^1}}}$ …..(2)

${V^1} = $ Volume of solid at temperature ${\text{T}} + \Delta {\text{T}}$

${\text{V}} = $ Volume of solid at temperature ${\text{T}}$

Since on increasing the temperature, solids liquids expand that is their volumes increases, so by equation

(1) & (2) Because density is inversely related to volume, if volume increases as temperature rises, density will fall.

30. Two bodies at different temperatures ${{\text{T}}_1}$, and ${{\text{T}}_2}$ are brought in thermal contact do not necessarily settle down to the mean temperature of ${{\text{T}}_1}$ and ${{\text{T}}_2}$?

Ans: Because the thermal capacity of two bodies may not always be equal, two bodies at different temperatures and in thermal contact do not always settle at their mean temperature equal.

31. The resistance of certain platinum resistance thermometer is found to be $2.56\Omega $ at ${0^0}{\text{c}}$ and $3.56\Omega$ at ${100^0}{\text{c}}$. When the thermometer is immersed in a given liquid, its resistance is observed to $5.06\Omega $. Determine the temperature of liquid?

Ans: Here, The Given:

${{\text{R}}_0} = $ Resistance at ${0^0}{\text{c}} = 2.56\Omega $

${{\text{R}}_{\text{t}}} = $ Resistance at temperature ${\text{T}} = {100^0}{\text{c}} = 3.56\Omega 100$

${{\text{R}}_{\text{t}}} = $ Resistance at unknown temperature t;

${{\text{R}}_{\text{t}}} = 5.06\Omega $

Since,

${\text{t}} = \dfrac{{{R_t} - {R_0}}}{{{R_{100}} - {R_0}}} \times 100$

$ = \dfrac{{(5.06 - 2.56)}}{{(3.56 - 2.56)}} \times 100$

$ = \dfrac{{2.5 \times 100}}{1}$

$ = \dfrac{{25}}{{10}} \times 100$

${\text{t}} = {250^0}{\text{c}}$

32. Calculate ${{\text{C}}_{\text{p}}}$ for air, given that ${{\text{C}}_{\text{v}}} = 0.162{\text{cal}}{{\text{g}}^{ - 1}}{K^{ - 1}}$ and density air at N.T. ${\text{P}}$ is $0.001293\;{\text{g/c}}{{\text{m}}^3}$ ?

Ans: Specific heat at constant pressure $ = {{\text{C}}_{\text{p}}} = $ ?

Specific heat at constant volume $ = {{\text{C}}_{\text{v}}} = 0.162{\text{Cal}}{{\text{g}}^{ - 1}}{K^{ - 1}}$

Now, ${\text{Cp}} - {\text{Cv}} = \dfrac{r}{J} = \dfrac{{PV}}{{TJ}}(\because PV = nRT)$

${\text{Or, CP}} - {\text{Cv}} = \dfrac{{P \times 1}}{{s \times TJ}}(s = $ Density)

${\text{Cp}} - {\text{Cv}} = \dfrac{{1.01 \times {{10}^6}}}{{273 \times 4.2 \times {{10}^7} \times 1.293 \times {{10}^{ - 3}}}}$

$ = \dfrac{{1.01 \times {{10}^{6 + 3 - 7}}}}{{273 \times 4.2 \times 1.293}}$

$ = \dfrac{{1.01 \times {{10}^2}}}{{1482.5}}$

$6.8 \times {10^{ - 4 + 2}}$

$Cp - Cv = 0.068$

${\text{Cp}} = 0.162 + 0.068$

${\text{Cp}} = 0.23{\text{Cal}}{{\text{g}}^{ - 1}}{K^{ - 1}}$

33. Develop a relation between the co-efficient of linear expansion, co-efficient superficial expansion and coefficient of cubical expansion of a solid?

Ans: Since the linear expansion co-efficient is = $\alpha  = \dfrac{{\Delta L}}{{L\Delta T}}$

$\Delta {\text{L}} = $ change in length

$L = $ length

$\Delta {\text{T}} = $ change in temperature

Similarly, co-efficient of superficial expansion $ = \beta  = \dfrac{{\Delta S}}{{S\Delta T}}$

$\Delta {\text{S}} = $ change in area

${\text{S}} = $ original area

$\Delta {\text{T}} = $ change in temperature

Co-efficient of cubical expansion, $ = {\text{Y}} = \dfrac{{\Delta V}}{{V\Delta T}}$

$\Delta {\text{V}} = $ change in volume

${\text{V}} = $ original volume

$\Delta {\text{T}} = $ change in temperature.

Now, $\Delta {\text{L}} = \alpha {\text{L}}\Delta {\text{T}}$

${\text{L}} + \Delta {\text{L}} = {\text{L}} + \alpha {\text{L}}\Delta {\text{T}}$

${\text{L}} + \Delta {\text{L}} = {\text{L}}(1 + \alpha \Delta {\text{T}}) \to (1)$

Similarly, ${\text{V}} + \Delta {\text{V}} = {\text{V}}(1 + {\text{Y}}\Delta {\text{T}}) \to (2)$

And ${\text{S}} + \Delta {\text{S}} = {\text{S}}(1 + \beta \Delta {\text{T}}) \to (3)$

Also, $({\text{V}} + \Delta {\text{V}}) = {({\text{L}} + \Delta {\text{L}})^3}$

${\text{V}} + \Delta {\text{V}} = {[L(1 + \alpha \Delta T)]^3}$

${\text{V}} + \Delta {\text{V}} = {{\text{L}}^3}\left( {1 + 3\alpha \Delta T + 3{\alpha ^2}\Delta {T^2} + {\alpha ^3}{T^3}} \right)$

Since ${\alpha ^2},{a^3}$ are negligible, so,

${\text{V}} + \gamma {\text{V}}\Delta {\text{T}} = {\text{V}}(1 + 3a\Delta {\text{T}})$ [as $\left. {{{\text{L}}^3} = {\text{V}}} \right]$

So, ${\text{V}} + \gamma {\text{V}}\Delta {\text{T}} = {\text{V}} + {\text{V}}3\alpha \Delta {\text{T}}$

$\gamma {\text{V}}\Delta {\text{T}} = 3\alpha \Delta {\text{T}}$

${\text{Y}} = 3{\text{a}}$

Similarly, $\beta  = 2\alpha $ [using ${{\text{L}}^2} = {\text{S}}$ (Area)]

So, $\alpha  = \dfrac{\beta }{2} = \dfrac{\gamma }{3}$

34. Calculate the amount of heat required to convert $1.00\;{\text{kg}}$ of ice at $ - {10^0}{\text{c}}$ into steam at ${100^0}{\text{c}}$ at normal pressure. Specific heat of ice $ = 2100\;{\text{J}}/{\text{kg/K}}$. Latent heat of fusion of ice = $3.36 \times {10^5}\;{\text{J/kg}}$, specific heat of water $ = 4200\;{\text{J/kg/K}}$. Latent heat of vaporization of water = $2.25 \times {10^6}\;{\text{J/kg}}?$

Ans: 

a) To raise the temperature of ice from to, heat is required from $ - {10^0}{\text{c}}$ to ${0^0}{\text{c}}$.

So, change in temperature $ = \Delta {\text{T}} = {{\text{T}}_2} - {{\text{T}}_1} = 0 - ( - 10) = {10^0}{\text{c}}$

So, $\Delta {{\text{Q}}_1} = {\text{cm}}\Delta {\text{T}}$

${\text{C}} = $ specific heat of ice

${\text{M}} = $ Mass of ice

$\Delta {\text{T}} = {10^0}{\text{c}}$

$\Delta {{\text{Q}}_1} = 2100 \times 1 \times 10 = 21000\;{\text{J}}$

b) Heat required to melt the ice to ${0^0}{\text{c}}$ water: -

$\Delta {Q_2} = mL$

${\text{L}} = $ Latent heat of fusion of ice $ = 3.36 \times {10^5}\;{\text{J}}/{\text{kg}}$

${\text{m}} = $ Mass of ice

$\Delta {{\text{Q}}_2} = 1 \times 3.36 \times {10^5}\;{\text{J}}/{\text{kg}}$

$\Delta {{\text{Q}}_2} = 3.36 \times {10^5}\;{\text{J}}$

$\Delta {{\text{Q}}_2} = 336000\;{\text{J}}$

c) Heat required to raise the temperature of water from ${0^0}{\text{c}}$ to ${100^0}{\text{c}}$ :-

$\Delta {\text{T}} = {\text{T}}2 - {\text{T}}1 = 100 - 0 = {100^0}{\text{c}}$

$\Delta {{\text{Q}}_3} = {\text{cm}}\Delta {\text{Tc}} = $ specific heat of water

$ = 4200 \times 1 \times 100$

$ = 420,000\;{\text{J}}$

d) Heat required to convert ${100^0}{\text{c}}$ water to steam at ${100^0}{\text{c}}$

$\Delta {Q_4} = mL\quad L = $ Latent heat of vaporization $ = 2.25 \times {10^6}\;{\text{J}}/{\text{kg}}$

$\Delta {{\text{Q}}_4} = 1 \times 2.25 \times {10^6}\;{\text{J/kg}}$

$\Delta {{\text{Q}}_4} = 2250000\;{\text{J}}$

$\therefore $ Total Heat required $ = \Delta {{\text{Q}}_1} + \Delta {{\text{Q}}_2} + \Delta {{\text{Q}}_3} + \Delta {{\text{Q}}_4}$

$\Delta Q$ total $ = 21000 + 336000 + 420000 + 2250000$

$\Delta Q$ total $ = 3027000\;{\text{J}}$

$\Delta Q$ total $ = 3.027 \times {10^6}\;{\text{J}}$

35. Why is mercury used in making thermometers?

Ans: Mercury are used Because mercury has a wide and useful temperature range and a uniform rate of expansion, so it is utilized to make thermometers.

36. How would a thermometer be different if glass expanded more with increasing temperature than mercury?

Ans: The scale of the thermometer would be upside down if glass expanded more than mercury with increasing temperature.

37. Show the variation of specific heat at constant pressure with temperature?

Ans: Temperature.

38. Two thermometers are constructed in the same way except that one has a spherical bulb and the other an elongated cylindrical bulb. Which one will response quickly to temperature change?

Ans: Because the surface area of the cylindrical bulb is higher than that of the spherical bulb, the thermometer with cylindrical bulb will respond fast to temperature changes.

39. State Carnot's Theorem?

Ans: We know that according to Carnot's Theorem, no engine operating between two temperatures can be more efficient than a Carnot's reversible engine operating between the same temperatures.

2 Marks Questions Part 1

1. A motor car tyre has a Pressure of four atmosphere at a room temperature of ${27^0}{\mathbf{C}}$. If the tyre suddenly bursts, calculate the temperature of escaping gas?

Ans: Since the tyre suddenly bursts, the change taking place is adiabatic, for adiabatic change: -

$\dfrac{{P_1^{Y - 1}}}{{T_1^4}} = \dfrac{{P_2^{Y - 1}}}{{T_2^4}}$

Or $T_2^4 = T_1^4{\left( {\dfrac{{{P_2}}}{{{P_1}}}} \right)^{Y - 1}}$ ……(1)

Hence, ${{\text{T}}_1} = 273 + 27 = 300\;{\text{K}}$

${{\text{P}}_1} = $ Initial Pressure; ${{\text{P}}_2} = $ final Pressure

So, $\dfrac{{{P_1}}}{{{P_2}}} = 4,4 = 1.4$

So, Putting the above values in equation (1)

$T_2^{14} = {(300)^{14}} \times {\left( {\dfrac{1}{4}} \right)^{1.4 - 1}}$

${\left( {{T_2}} \right)^{14}} = {(300)^{1.4}} \times {\left( {\dfrac{1}{4}} \right)^{04}}$

Taking 1.4 Power:

${T_2} = {(300)^{\dfrac{{14}}{{14}}}} \times {\left( {\dfrac{1}{4}} \right)^{\dfrac{{0.4}}{{1.4}}}}$

${{\text{W}}_1} =  - 150\;{\text{J}}$ ….(2)

Work done by the gas in the process ${\text{B}} \to {\text{C}}$ is: 

${W_2} =  - [$ area under the curve BC]

${W_2} =  - [($ area of $\Delta {\text{BCD}}) + $ area of rectangle ${\text{CBDEF}}]$

$ =  - \left( {\left[ {\dfrac{1}{2} \times } \right.} \right.$ Base $ \times $ Height $] + [$ Length $ \times $ Breadth $\left. ] \right)$

$\left( {\left[ {\dfrac{1}{2} \times {\text{CD}} \times {\text{BD}}} \right] + [{\text{CD}} \times {\text{EF}}]} \right)$

$ =  - \left( {\left[ {\dfrac{1}{2} \times \left( {3 \times {{10}^5}} \right) \times 200 \times {{10}^{ - 6}}} \right] + \left[ {2 \times {{10}^5} \times 200 \times {{10}^{ - 5}}} \right]} \right)$

${W_2} =  - 70 J$ …..(3)

Adding equation (2) and (3):

Net work done by the gas in the whole process is 

${\text{W}} = {{\text{W}}_1} + {{\text{W}}_2}$

${T_2} = 300 \times {\left( {\dfrac{1}{4}} \right)^{\dfrac{{0.4}}{{14}}}}$

${\text{W}} = 150 - 70 =  - 22{\text{OJ}}$

${T_2} = 300 \times {\left( {\dfrac{1}{4}} \right)^{\dfrac{{{y^4}}}{{7}}}}$

${{\text{T}}_2} = 201.8\;{\text{K}}$

$\therefore {{\text{T}}_2} = 201.8 - 273 =  - {71.2^0}{\text{C}}$

2. How does Carnot cycle operates?

Ans: A Carnot cycle operates a follow: -

1) It receives thermal energy isothermally from some hot reservoir maintained at a constant high temperature ${{\text{T}}_{\text{H}}}$

2) It rejects thermal energy isothermally to a constant low-temperature reservoir $\left( {{{\text{T}}_2}} \right.$ ).

3) The change in temperature is reversible adiabatic process.

Such a cycle, which consist of two isothermal processes bounded by two adiabatic processes, is called Carnot cycle.

3. Calculate the work done by the gas in going from the ${\text{P}} - {\text{V}}$ graph of the thermodynamic behaviour of a gas from point A to point B to point C?

Ans: Work done by the gas in the process ${\text{A}} \to {\text{B}}$ is

${{\text{W}}_1} =  - $ (Area under curve A B)

$ =  - \left[ {\left( {{P_{AB}}} \right) \times \left( {{V_2} - {V_1}} \right)} \right]$

$ =  - \left[ {5 \times {{10}^5} \times (800 - 500) \times {{10}^{ - 5}}} \right]$

${{\text{P}}_{{\text{AB}}}} = 500\;{\text{Pa}}$

$ = 5 \times {10^5}\;{\text{N/}}{{\text{m}}^2}$

$\left( {{V_2} - {V_1}} \right) = (300){\text{c}}{{\text{m}}^3}$ or $300 \times {10^{ - 6}}\;{{\text{m}}^3}$

4. Why does absolute zero not correspond to zero energy?

Ans: The total energy of a gas is the sum of kinetic and potential energy of its molecules. Since the kinetic energy is a function of the temperature of the gas. Hence at absolute zero, the kinetic energy of the molecules ceases but potential energy is not zero. So, absolute zero temperature is not the temperature of zero energy.

5. State the Second law of thermodynamics and write 2 applications of it?

Ans: According to second law of thermodynamics, when a cold body and a hot body are brought into contact with each other, heat always from hot Body to the cold body. Also, that no heat engine that works in cycle completely converts heat into work. Second law of thermodynamics is used in working of heat engine and of refrigerator.

6. At ${0^0}{\text{C}}$ and normal atmospheric pressure, the volume of $1\;{\text{g}}$ of water increases from $1\;{\text{c}}{{\text{m}}^3}$ to $1.091\;{\text{c}}{{\text{m}}^3}$ on free zing. What will be the change in its internal energy? Normal atmospheric pressure is $1.013 \times {10^5}\;{\text{N}}\mid {{\text{m}}^2}$ and the latent heat of melting of ice is $80{\text{cal}}/{\text{g}}$ ?

Ans: Since, heat is given out by $1\;{\text{g}}$ of water in freezing is

${\text{m}} = $ Mass of water $ = 1\;{\text{g}}$

$Q =  - (mLf)Lf = $ Latent heat of melting of ice $ = 80{\text{cal/}}g$

[Negative sign is assigned to Q because it is given out by water]

During freezing, the water expands against atmospheric pressure. Hence, external work done (W) by water is: - ${\text{W}} = {\text{P}} \times \Delta {\text{V}}$

${\text{P}} = 1.013 \times {10^5}\;{\text{N/}}{{\text{m}}^2};\Delta {\text{V}} = 1.091 - 1 = 0.091\;{\text{c}}{{\text{m}}^3} = 0.091 \times {10^{ - 6}}\;{{\text{m}}^3}$

$\Delta {\text{V}} = {{\text{V}}_2} - {{\text{V}}_1};{{\text{V}}_2} = $ final volume $ = 1.91\;{\text{c}}{{\text{m}}^3}$

${{\text{V}}_1} = $ Initial volume $ = 1\;{\text{c}}{{\text{m}}^3}$

So, ${\text{W}} = \left( {1.013 \times {{10}^5}} \right) \times \left( {0.091 \times {{10}^{ - 5}}} \right)$

${\text{W}} = 0.0092\;{\text{J}}$

Since, $1{\text{cal}} = 4.2\;{\text{J}}$ so,

$\text{W} = \dfrac{{0.0092}}{{4.2}} = 0.0022{\text{cal}}$

Since the work has been done by ice, it will be taken positive.

Acc. to first law of thermodynamics,

${\text{Q}} = \Delta {\text{u}} + {\text{W}}\Delta {\text{u}} = $ change in internal energy

So, $\Delta {\text{u}} = {\text{Q}} - {\text{W}}$

$\Delta u =  - 80.0022 Cal$

The negative sign indicates that the internal energy of water decreases on freezing.

7. Two different adiabatic paths for the same gas intersect two thermals at ${{\text{T}}_1}$ and ${{\text{T}}_2}$ as shown in P-V diagram. How does $\dfrac{{VA}}{{VD}}$ Compare with $\dfrac{{VB}}{{VC}}$ ?

Ans: Now, A B and C D are isothermals at temperature ${{\text{T}}_1}$ and ${{\text{T}}_2}$ respectively and ${\text{BC}}$ and ${\text{AD}}$

are adiabatic.

Since points A and D lie on the same adiabatic.

$\therefore {T_A}V_A^{Y - 1} = {T_D}V_D^{I - 1}$

${{\text{T}}_1}\;{{\text{V}}_{\text{A}}}{\text{Y}} - 1 = {{\text{T}}_2}\;{{\text{V}}_{\text{D}}}{\text{Y}} - 1$

$\dfrac{{{T_1}}}{{{T_2}}} = {\left( {\dfrac{{{V_D}}}{{{V_A}}}} \right)^{Y \cdot 1}}$

Also, points B and C lie on the same adiabatic,

${{\text{T}}_{\text{B}}}{\text{V}}_{\text{B}}^{{\text{Y}} \cdot 1} = {{\text{T}}_{\text{C}}}{{\text{V}}_{\text{C}}}{\text{Y}} \cdot 1$

or ${{\text{T}}_1}\;{{\text{V}}_{\text{B}}}{\text{Y}} - 1 = {{\text{T}}_2}\;{{\text{V}}_{\text{C}}}{\text{Y}} - 1$

$\because \dfrac{{{T_1}}}{{{T_2}}} = {\left( {\dfrac{{{V_C}}}{{{V_B}}}} \right)^{Y \cdot 1}}$From equation 1) & 2)

${\left( {\dfrac{{{\text{VD}}}}{{{\text{VA}}}}} \right)^{{\text{x}} \cdot 1}} = {\left( {\dfrac{{{\text{VC}}}}{{{\text{VB}}}}} \right)^{{\text{Y}} \cdot 1}}$

$\dfrac{{VD}}{{VA}} = \dfrac{{VC}}{{VB}}$

$\dfrac{{VA}}{{VD}} = \dfrac{{VB}}{{VC}}$

8. The internal energy of a compressed gas is less than that of the rarefied gas at the same temperature. Why?

Ans: The internal energy of a compressed gas is less than that of ratified gas at the same temperature because in compressed gas, the mutual attraction between the molecules increases as the molecules comes close. Therefore, potential energy is added to internal energy and since potential energy is negative, total internal energy decreases.

9. Consider the cyclic process A B C A on a sample 2 mol of an ideal gas as shown. The temperature of the gas at A and B are300 K and 500K respected. Total of 1200 J of heat is withdrawn from the sample. Find the work done by the gas in part BC?

Ans: The change in internal energy during the cyclic process is zero. Therefore, heat supplied to the gas is equal to work done by it,

$\therefore {{\text{W}}_{{\text{AB}}}} + {{\text{W}}_{{\text{BC}}}} + {{\text{W}}_{{\text{CA}}}} =  - 1200\;{\text{J}}$ …. (1)

(- ve because the cyclic process is traced anticlockwise the net work done by the system is negative)

The work done during the process ${\text{AB}}$ is

${{\text{W}}_{{\text{AB}}}} = {{\text{P}}_{\text{A}}}\left( {{{\text{V}}_{\text{B}}} - {{\text{V}}_{\text{A}}}} \right) = {\text{nR}}\left( {{{\text{T}}_{\text{B}}} - {{\text{T}}_{\text{A}}}} \right)\left( {{\text{Q}}{{\text{P}}_{\text{V}}} = {\text{nRT}}} \right)$

${\text{WAB}} = 2 \times 8.3(500 - 300) = 3320\;{\text{J}}$ …..(2)

${\text{R}}$ = Universal gas constant

${\text{N}} = $ No. of volume

Since in this process, the volume increases, the work done by the gas is positive.

Now, WCA $ = 0$ ( $\because $ volume of gas remains constant)

$\therefore 3320 + {\text{WBC}} + {\text{O}} =  - 1200$ [Using equation (1) \& (2)]

${\text{WBC}} =  - 1200 - 3320$

${{\text{W}}_{{\text{BC}}}} =  - 4520\;{\text{J}}$

10. A refrigerator placed in a room at $300\;{\text{K}}$ has inside temperature 264K. How many calories of heat shall be delivered to the room for each $1\;{\text{K}}$ Cal of energy consumed by the refrigerator, ideally?

Ans: Given Data:

High temperature, ${{\text{T}}_{\text{H}}} = 300\;{\text{K}}$

Low temperature, ${{\text{T}}_{\text{h}}} = 264\;{\text{K}}$

Energy $ = 1\;{\text{K}}$ cal.

Co - efficient of performance, is given by: -

${\text{COP}} = \dfrac{{{{\text{T}}_{\text{H}}}}}{{{{\text{T}}_{\text{H}}} - {{\text{T}}_{\text{L}}}}} = \dfrac{{264}}{{300 - 264}} = \dfrac{{22}}{3}$

Now, COP $ = \dfrac{{{Q_L}}}{W}$

${{\text{Q}}_{\text{L}}} = $ heat rejected

${{\text{Q}}_{\text{L}}} = {\text{COP}} \times {\text{W}}$

${{\text{Q}}_{\text{L}}} = \dfrac{{22}}{3} \times 1 = \dfrac{{22}}{3}{\text{Cal}}$

The mechanical work done by the compressor of the refrigerator is: -

${\text{W}} = {{\text{Q}}_{\text{H}}} - {{\text{Q}}_{\text{L}}}$

${{\text{Q}}_{\text{H}}} = {\text{W}} + {{\text{Q}}_{\text{L}}}$

${{\text{Q}}_{\text{H}}} = \dfrac{{22}}{3} + 1$

${Q_H} = \dfrac{{25}}{3}Cal$

${{\text{Q}}_{\text{H}}} = 8.33\;{\text{K}}$ Cal

11. If the door of a refrigerator is kept open in a room, will it make the room warm or cool?

Ans: Refrigerator is a heat engine that works in the other manner, extracting heat from a cold body and converting it to heat. Because it emits more heat into the room than it absorbs. As a result, the overall effect is an increase in room temperature.

12. The following figure shows a process A B C A per formed on an ideal gas, find the net heat given to the system during the process?

Ans: The change in internal energy is zero because the process is cyclic. As a result, the system receives the same amount of heat as it does work. In the process, the net work done by the gas.

ABCA is: -

${\text{W}} = {{\text{W}}_{{\text{AB}}}} + {{\text{W}}_{{\text{BC}}}} + {{\text{W}}_{{\text{CA}}}}$

Now ${{\text{W}}_{{\text{AB}}}} = 0(\because $ Volume remains constant)

During the path BC, temperature remains constant. So, it is an isothermal process. So, ${{\text{W}}_{{\text{BC}}}} = $ ${\text{nR}}{{\text{T}}_2}$ Loge $\dfrac{{{V_2}}}{{{V_1}}}$

During the CA, Vα T so that $\dfrac{V}{T}$ is constant.

$P = \dfrac{{nRT}}{V} = $constant

$\therefore $ Work done by the gas during the part CA is:-

${{\text{W}}_{{\text{CA}}}} = {\text{P}}\left( {{{\text{V}}_1} - {{\text{V}}_2}} \right)$

$ = {\text{nR}}\left( {{{\text{T}}_1} - {{\text{T}}_2}} \right)$

$ =  - {\text{nR}}\left( {{{\text{T}}_2} - {{\text{T}}_1}} \right) \to $ Using equation 1)

${\text{W}} = 0 + {\text{nR}}{{\text{T}}_2}$ Loge $\dfrac{{{V_2}}}{{{V_1}}} - {\text{nR}}\left( {{{\text{T}}_2} - {{\text{T}}_1}} \right)$

$W = nR\left[ {{T_2}\log e\dfrac{{{V_2}}}{{{V_1}}} - \left( {{T_2} - {T_1}} \right)} \right]$

13. A certain gas at atmospheric pressure is compressed adiabatically so that its volume becomes half of its original volume. Calculate the resulting pressure?

Ans: Let the Given Data:

original volume, ${{\text{V}}_1} = {\text{V}}$

final volume ${{\text{V}}_2} = \dfrac{V}{2}$  (volume become half)

Initial pressure ${{\text{P}}_1} = 0.76\;{\text{m}}$ of ${\text{Hg}}$ column

Final pressure ${{\text{P}}_2}$ after compression =?

As the change is adiabatic, so

${P_1}V_1^y = {P_2}V_2^y{\text{Y}} = \dfrac{{CP}}{{cv}} = 1.4$ for air

${{\text{P}}_2} = {{\text{P}}_1}{\left( {\dfrac{{{V_1}}}{{{V_2}}}} \right)^4}$

$ = 0.76 \times {\left( {\dfrac{V}{{V/2}}} \right)^{1.4}}$

${{\text{P}}_2} = 0.76 \times {(2)^{1.4}}$

${{\text{P}}_2} = 2\;{\text{m}}$ of ${\text{Hg}}$ column

${{\text{P}}_2} = {\text{hsg}}$

${{\text{P}}_2} = 2.672 \times {10^5}\;{\text{N/}}{{\text{m}}^2}$

${{\text{P}}_2} = 2 \times \left( {13.6 \times {{10}^3}} \right) \times 9.8$

${\text{h}}$ = height of ${\text{Hg}}$ column

${\text{s}} = $ Density of air

${\text{g}} = $ Acceleration due to gravity

14. Why is conversion of heat into work not possible without a sink at lower temperature?

Ans: A portion of the heat energy absorbed from the source must be rejected in order to turn heat energy into work on a continual basis. We need a sink to turn heat into work because heat energy can only be rejected to a body at a lower temperature.

15. Write the sign conventions for the heat and work done during a thermodynamic process?

Ans: The sign conventions for the heat and work done during a thermodynamic process are: 

1) When heat is given to a system, the value of d is positive; however, when heat is supplied by a system, the value of d is negative.

2) When a gas expands, the work done is positive; however, when a gas compresses, the work done is negative.

16. Does the working of an electric refrigerator defy second law of thermodynamics?

Ans: No, it does not violate the second law; this is due to the compressor's or this heat transfer's exterior work.

17. A Carnot engine absorb $6 \times {10^5}$ Cal at ${227^0}{\text{c}}$ calculate work done per cycle by the engine if it sinks is at ${127^0}{\mathbf{c}}$ ?

Ans: Given data:

heat abs or bed $ = {{\text{Q}}_1} = 6 \times {10^5}{\text{Cal}}$.

Initial temperature $ = {{\text{T}}_1} = {227^0}{\text{c}} = 227 + 273 = 500\;{\text{K}}$

Final temperature $ = {{\text{T}}_2} = {127^0}{\text{c}} = 127 + 273 = 400\;{\text{K}}$

As, for Carnot engine;

$\dfrac{{{Q_2}}}{{{Q_1}}} = \dfrac{{{T_2}}}{{{T_1}}}$

${Q_2} = {Q_1}\dfrac{{{T_2}}}{{{T_1}}}$

${{\text{Q}}_2} = \dfrac{{400}}{{500}} \times 6 \times {10^5}$

${{\text{Q}}_2} = 4.8 \times {10^5}{\text{Cal}}$

${{\text{Q}}_2} = $ Final heat emitted

As ${\text{W}} = {{\text{Q}}_1} - {{\text{Q}}_2} = 6 \times {10^5} - 4.8 \times {10^5}$

$ = 1.2 \times {10^5}{\text{cal}}$

Work $ = {\text{w}} = 1.2 \times {10^5} \times 4.2\;{\text{J}}$

Dore $ = 5.04 \times {10^5}\;{\text{J}}$

18. How does second law of thermodynamics explain expansion of gas?

Ans: Since from second law,

${\text{dS}} \geqslant {\text{O}}\quad {\text{dS}} = $ change in entropy

The thermodynamic probability of a gas increases as it expands, and thus its entropy increases as well. Because entropy cannot decrease as a result of the second law, gas molecules move from one partition to the next.

19. Why is it hotter at the same distance over the top of the fire than in front of it?

Ans: Heat is only received by radiation at a position in front of the fire, but heat is received by both radiation and convection at a point above the fire. As a result, the outcome.

20. A metal rod of length $20\;{\text{cm}}$ and diameter $2\;{\text{cm}}$ is covered with a non-conducting substance. One of it ends is maintained at ${100^0}{\text{c}}$ while the other is at ${0^0}{\text{c}}$. It is found that 25 g of ice melts in 5 min calculate coefficient of thermal conductivity of metal?

Ans: Given:

Length of $\operatorname{rod}  = \Delta {\text{x}} = 20\;{\text{cm}} = 2 \times {10^{ - 3}}\;{\text{m}}$

Diameter $ = 2\;{\text{cm}}$

${\text{R}} = {10^{ - 2}}\;{\text{m}}$

Area of cross-section $ = \pi {{\text{r}}^2}$

$ = \pi {\left( {{{10}^{ - 2}}} \right)^2}$

$ = {10^{ - 4}}\pi $ s ${\text{m}}$

$\Delta {\text{T}} = {T_2} - {T_2} = 100 - 0 = {100^0}{\text{c}}$ Mass of ice melted $ = {\text{m}} = 25\;{\text{g}}$ Latent heat office $ = 80{\text{cal}}/{\text{g}}$

Heat conducted, $\Delta {\text{Q}} = {\text{mL}}$ $ = 25 \times 80$

$ = 2000{\text{cal}}$

$ = 2000 \times 4.2\;{\text{J}}$

$\Delta {\text{t}} = 5\;{\text{min}} = 300\;{\text{s}}$

So, $\dfrac{{\Delta Q}}{{\Delta t}} = {\text{KA}}\dfrac{{\Delta T}}{{\Delta x}}$

${\text{K}} = \dfrac{{\Delta Q/\Delta t}}{{A\Delta T/\Delta x}} = \dfrac{{\Delta Q\Delta x}}{{\Delta tA\Delta T}}$

$ = \dfrac{{2000 \times 4.2 \times 20 \times {{10}^{ - 2}}}}{{300 \times {{10}^{ - 4}}\pi  \times 100}}$

 K= 1.78 J/s.

${\text{K}} = $ coefficient of thermal conductivity

21. Calculate the temperature in Kelvin at which a perfectly black body radiates at the rate of $5.67{\text{w}}/{\text{c}}{{\text{m}}^2}?$

Ans: Given Date:

$E = 5.67{\text{w/c}}{{\text{m}}^2};{\text{E}} = $ energy radiated

$ = 5.67 \times {10^7}{\text{erg/s/c}}{{\text{m}}^2}$

$\sigma  = $ Stefan's constant $ = 5.67 \times {10^{ - 5}}$ ergs ${\text{/s/c}}{{\text{m}}^2}{\text{/}}{{\text{K}}^4}$, from Stefan's law

${\text{E}} = \sigma {{\text{T}}^4}$

$T = {\left( {\dfrac{E}{\sigma }} \right)^{\dfrac{1}{4}}}$

${\text{T}} = {\left( {\dfrac{{5.67 \times {{10}^7}}}{{5.67 \times 10{ - ^5}}}} \right)^{\dfrac{1}{4}}}$

${\text{T}} = {\left( {{{10}^{12}}} \right)^{\dfrac{1}{4}}} = {10^3} = 1000\;{\text{K}}$

22. How do you explain the emission of long - wavelength by the object at low temperature?

Ans: According to Wein's law: 

$\lambda m\alpha \dfrac{1}{T}$

$\lambda m = $ constant ${\text{T}}$

i.e., Because temperature and wavelength are inversely proportional, if the temperature is lower, the wavelength will be longer. The wavelength will be short if the temperature is high.

23. If the radiation from the moon gives maxima at $\lambda  = 4700\;{{\text{A}}^0}$  and $\lambda  = 14 \times {10^{ - 6}}\;{\text{m}}$. What conclusion can be drawn from the above information?

Ans: According to Wien’s displacement law,

$\lambda m\;{\text{T}} = {\text{b}}$

Now, according to the question, $2\;{\text{m}} = 4700\;{{\text{A}}^0} = 4700 \times {10^{ - 10}}\;{\text{m}}$

${{\text{T}}_1} = $ Temperature of moon,

${{\text{T}}_1} = \dfrac{b}{{\lambda m}}$

${\text{b}} = 2.9 \times {10^{ - 3}}{\text{mK}}$

${T_1} = \dfrac{{2.9 \times {{10}^{ - 3}}}}{{4700 \times {{10}^{ - 10}}}}$

$ = \dfrac{{29 \times {{10}^{ - 4}} \times {{10}^{10}}}}{{4700}}$

${T_1} = 6170\;{\text{K}}$

Let the temperature corresponding to $\lambda m = 14 \times {10^{ - 6}}m = {T_2}$

So, ${{\text{T}}_2} = \dfrac{b}{{\lambda m}}$

${{\text{T}}_2} = \dfrac{{2.9 \times {{10}^{ - 3}}{\text{mK}}}}{{{{14}^ - } \times {{10}^{ - 6}}\;{\text{m}}}} = \dfrac{{29 \times {{10}^{ - 4 + 6}}}}{{14}}K = 207\;{\text{K}}$

24. Differentiate between conduction, convection and radiation?

Ans: Difference between conduction, convection and radiation:

25.The tile floor feels colder than the wooden floor even though both floor materials are at same temperature. Why?

Ans: This is due to the fact that tile conducts heat better than wood. The heat transferred from our feet to the wood does not dissipate quickly. As a result, the wood quickly heats up to the temperature of our foot on its surface. The tile, on the other hand, transfers heat away quickly and can thus absorb more heat from our foot, lowering its surface temperature.

2 Marks Questions Part 2

26.A room has a $4\;{\text{m}} \times 4\;{\text{m}} \times 10\;{\text{cm}}$ concrete roof $\left( {{{\text{K}}_1} = 1.26{\text{w/m}}{{\text{/}}^0}{\text{C}}} \right).$ At some instant, the temperature outside is ${46^0}{\text{c}}$ and radius ${32^0}{\text{c}}$.

1) Calculate amount of heat flowing per second into the room through the roof.

2) If bricks $\left( {{{\text{K}}_2} - 0.56{\text{w/m}}{{\text{/}}^0}{\text{c}}} \right)$ of thickness $7.5\;{\text{cm}}$ are laid down on roof, calculate the new rate of heat flow under the same temperature conditions?

Ans: Given Data Be:

1) Area of roof $ = 4 \times 4 = 16\;{{\text{m}}^2}$

Thickness of roof, ${{\text{x}}_1} = 10\;{\text{cm}} = 0.1\;{\text{m}}$,

Thermal resistance of the roof is given by: -

${{\text{R}}_1} = \dfrac{{{{\text{x}}_1}}}{{\;{{\text{K}}_1}\;{{\text{A}}_1}}} = \dfrac{{0.1}}{{1.26 \times 16}} = 4.96 \times {10^{ - 3}}{\text{cc}}/{\text{w}}$

$\therefore $ Rate of heat flow through the roof is: -

${{\text{H}}_1} = \dfrac{\theta }{{\text{t}}} = \dfrac{{{\theta _1} - {\theta _2}}}{{\text{R}}} = \dfrac{{46 - 32}}{{4.96 \times {{10}^{ - 3}}}}$

${{\text{H}}_1} = \dfrac{{14 \times {{10}^3}}}{{4.96}}$

${{\text{H}}_1} = 2822{\text{w}}$

2) The thermal resistance of the brick is given by: -

${{\text{R}}_2} = \dfrac{{{{\text{x}}_2}}}{{\;{{\text{K}}_2}\;{{\text{A}}_2}}} = \dfrac{{7.5 \times {{10}^{ - 2}}}}{{0.65 \times 16}} = 7.2 \times {10^{ - 3}}{\text{CC}}/{\text{W}}$

The equivalent thermal resistance of the roof now is: 

$R = {{\text{R}}_1} + {{\text{R}}_2} = (4.96 + 7.2) \times {10^{ - 3}} = 1.216 \times {10^{ - 2}}{\text{oC}}/{\text{W}}$

$\therefore $ Rate of heat through the roof is: 

${{\text{H}}_2} = \dfrac{\theta }{{\text{t}}} = \dfrac{{\theta 1 - \theta 2}}{{\text{R}}} = \dfrac{{46 - 32}}{{1.216 \times {{10}^{ - 2}}}} = 1152\;{\text{W}}$

27.A bar o copper of length $75\;{\text{cm}}$ and a bar of length $125\;{\text{cm}}$ are joined end to end. Both are of circular cross - section with diameters $2\;{\text{cm}}$. The free ends of copper and steel are maintained at ${100^0}{\text{c}}$ and ${0^0}{\text{c}}$ respectively. The surfaces of the bars are thermally insulated. What is the temperature of copper - steel junction? Thermal conductivity of copper $ = 9.2 \times {10^{ - 2}}{\mathbf{k}}$ Cal $/{\mathbf{m}}{/^0}{\mathbf{c}}/$ s and that of steel is $1.1 \times {10^{ - 2}}{\mathbf{kcal}}/{\mathbf{m}}{/^0}{\mathbf{c}}/{\mathbf{s}}?$

Ans: Let the Given data:

${l_1} = $ lengths of copper bars ${\text{AB}}$

${l_2} = $ length of steel bars ${\text{BC}}$.

${\Theta _1} = $ temperature of free ends ${\text{A}}$

${\Theta _2} = $ temperature of free ends ${\text{C}}$.

$\Theta  = $ temperature of copper - steel.

In steady state, the heat flowing per second through two bars is the same i.e

${{\text{H}}_1} = {{\text{H}}_2}$

$\dfrac{{{K_1}A\left( {{\theta _1} - {\theta _2}} \right)}}{{{l_1}}} = \dfrac{{{K_2}A\left( {\theta  - {\theta _2}} \right)}}{{{l_2}}}$

$\dfrac{{{K_1}{\theta _1}}}{{{l_1}}} - \dfrac{{{K_1}{\theta _2}}}{{{l_1}}} = \dfrac{{{K_2}\theta }}{{{l_2}}} - \dfrac{{{K_2}{\theta _2}}}{{{l_2}}}$

or $\dfrac{{{K_1}{\theta _1}}}{{{l_1}}} + \dfrac{{{K_2}{\theta _2}}}{{{l_2}}} = \dfrac{{{K_2}\theta }}{{{l_2}}} + \dfrac{{{K_1}\theta }}{{{l_1}}}$

$\dfrac{{{K_1}}}{{{l_1}}}{\theta _1} + \dfrac{{{K_2}}}{{{l_2}}}{\theta _2} = {\text{O}}\left( {\dfrac{{{K_1}}}{{{l_1}}} + \dfrac{{{K_2}}}{{{l_2}}}} \right)$

$\therefore $ Temperature of junction $ = \theta : \to $

28.Two rods A and B are of equal length. Each rod has its ends at temperatures ${{\text{T}}_1}$ and ${{\text{T}}_2}$. What is the condition that will ensure equal rates of flow of heat through the rods ${\text{A}}$and B?

Ans: Since $\theta  = \dfrac{{{\text{KA}}\left( {{\theta _1} - {\theta _2}} \right)t}}{{\text{x}}}$

$\Theta  = $ heat flow

${\text{K}} = {\text{co}} - $ efficient of thermal conductivity

${\text{A}} = $ Cross - Sectional Area

$\Theta 1 = $ Temperature of hot body

$\Theta 2 = $ Temperature of cold body

${\text{X}} = $ distance between hot and cold faces

${\text{t}} = $ time

For rod A:

$\dfrac{{{\theta _A}}}{t} = \dfrac{{{K_A}\left( {{T_1} - {T_2}} \right){A_A}}}{x}$

And $\dfrac{{{\theta _A}}}{t} = \dfrac{{{K_A}\left( {{T_1} - {T_2}} \right){A_B}}}{x}$

For equal rates of flow, $\dfrac{{{\theta _A}}}{t} = \dfrac{{{\theta _B}}}{t}{K_A}{A_A} = {K_B}{A_B}$

29. A layer of ice $10\;{\text{cm}}$ thick is formed on a pond. The temperature of air is $ - {10^0}{\text{C}}$. Calculate how long it will take for the thickness of ice to increase by $1\;{\text{mm}}$. Density of

ice $ = 1\;{\text{g/c}}{{\text{m}}^3};$ Thermal conductivity of ice =0.005Cal/s/cm/C Latent heat of ice = 80Cal /g?

Ans: Let ${\text{t}} = $ time required to increase the thickness of ice by $1\;{\text{mm}}( = 0.1\;{\text{cm}})$

Mass of ice required to be formed is: -

${\text{m}} = $ Volume ${\text{x}}$ Density

Let ${\text{A}} = $ Area of upper surface

Volume = Area ${\text{x}}$ Thickness

$ = {\text{A}} \times 0.1$

${\text{m}} = ({\text{A}} \times 0.1) \times 1$

${\text{m}} = 0.1\;{\text{A}} gram$ ……(1)

Now, heat must flow from lower surface to the upper surface of ice and finally into atmosphere.

$\Theta  = $ heat that flows out of pond into atmosphere.

$\lambda  = $ Latent heat of ice

${\text{m}} = $ Mass of ice

${\text{k}} = {\text{co}} - $ efficient of thermal conductivity A = Cross - sectional Area${\text{t}} = $ time${\text{x}} = $ Distance between hot and cold surface

${\theta _1} = $ temperature of hot surface

${\theta _2} = $ temperature of cold surface

$\therefore \theta  = {\text{mL}};$

$\Theta  = 0.1 \times {\text{A}} \times 80$ (Using equation 1)

$\Theta  = 8 A cal$ ….(2)

But $\theta  = \dfrac{{{\text{KA}}\left( {{\theta _1} - {\theta _2}} \right)t}}{{\text{x}}}$

Using equation (2)

$8\;{\text{A}} = \dfrac{{{\text{KA}}\left( {{\theta _1} - {\theta _2}} \right)r}}{{\text{x}}}$

${\text{t}} = \dfrac{{8{\text{x}}}}{{{\text{K}}\left( {{\theta _1} - {\theta _2}} \right)}}$

Now, ${\text{x}} = 10\;{\text{cm}}$

K=0.005 Cal/cm/∆/0C

${\theta _1} - {\theta _2} = 0 - ( - 10) = {10^0}{\text{C}}$

${\text{t}} = \dfrac{{8 \times 10}}{{0.005 \times 10}} = 1600{\text{Sec}}$

30. Two conducting slabs of thermal conductivities ${{\text{K}}_1}$ and ${{\text{K}}_2}$ are joined as shown in the figure. The temperature of the ends of slab are ${\theta _1}$ and ${\theta _2}\left( {{\theta _1} > {\theta _2}} \right).$ Find the final temperature of $(\theta {\mathbf{m}})$ ?

Ans: Let the Given Data:

${\theta _1} = $ temperature of hot slab

${\Theta _2} = $ temperature of cold slab

${{\text{K}}_1} = {\text{Co}} - $ efficient of thermal conductivity of hot slab

${{\text{K}}_2} = $ Co - efficient of thermal conductivity of cold slab

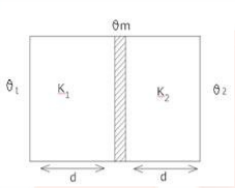
${\Theta _{\text{m}}} = $ final temperature

${\text{d}} = $ Distance ${\text{b}}/{\text{w}}$ hot and cold surface

${\text{A}} = $ Area of cross - section

${\text{t}} = $ time

Now, since is steady state, the rate of heat transfer in both the slabs is same i.

$\dfrac{{{\theta _1}}}{{\text{t}}} = \dfrac{{{\theta _2}}}{{\text{t}}}$

or $\dfrac{{{{\text{K}}_1}A\left( {{\theta _1} - {\theta _{\text{m}}}} \right)}}{{{d^\prime }}} = \dfrac{{{{\text{K}}_2},\;{\text{A}}\left( {{\theta _{\text{m}}} - {\theta _2}} \right)}}{{{d^\prime }}}$

${K_1}\left( {{\theta _1} - {\theta _m}} \right) = {K_2}\left( {{\theta _m} - {\theta _2}} \right)$

${\Theta _1} - {\theta _{\text{m}}} = $ because first heat flows from ${\theta _1}$ to the junction

${\Theta _2} - {\theta _{\text{m}}} = $ then heat flows from junction to second surface

So, ${K_1}\left( {{\theta _1} - {\theta _m}} \right) = {K_2}\left( {{\theta _m} - {\theta _2}} \right)$

${K_1}{\theta _1} - {K_1}{\theta _m} = {K_2}{\theta _m} - {K_2}{\theta _2}$

${K_1}{\theta _1} + {K_2}{\theta _2} = {K_2}{\theta _2} + {K_1}{\theta _m}$

${K_1}{\theta _1} + {K_2}{\theta _2} = {\theta _m}\left( {{K_1} + {K_2}} \right)$

So, ${\theta _m} = \dfrac{{{K_1}{\theta _1} + {K_2}{\theta _2}}}{{{K_1} + {K_2}}}$

31. The ends of the two rods of different materials with their thermal conductivities, radii of cross - section and length in the ratio 1: 2 are maintained at the same temperature difference. If the rate of flow of heat through the larger rod is 4 Cal $\mid $ s, what is the rate of flow through the shorter rod?

Ans: Let Given Data:

${{\text{K}}_1} = $ thermal conductivity of first region

${{\text{K}}_2} = $ thermal conductivity of second region

${{\text{r}}_1} = $ radius of cross section of first region

${{\text{r}}_2} = $ radius of cross - section of second region

${{\text{l}}_1} = $ length of first region

${{\text{l}}_2} = $ length of second region

${\theta_1} = $ heat flow of first region

${theta_2} = $ heat flow of second region

Now, $\dfrac{{{K_1}}}{{{K_2}}} = \dfrac{1}{2}$

Also, $\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{1}{2}$ and $\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{1}{2}($ Given)

and $\dfrac{{{\theta _2}}}{t} = $ rate of flow of heat from second region

$\dfrac{{{\theta _2}}}{{\text{t}}} = 4{\text{cal}}/{\text{sec}}$

${\theta _1} - {\theta _2} = $ Same.

Now, we know, $\dfrac{\theta }{{\text{t}}} = \dfrac{{{\text{KA}}\left( {{\theta _1} - {\theta _2}} \right)}}{{\text{x}}}$

$\dfrac{\theta }{{\text{t}}} = \dfrac{{{\text{K}}\pi {{\text{r}}^2}\left( {{\theta _1} - {\theta _2}} \right)}}{{}}$

So, Let

${\theta _1} = {{\text{T}}_1}$

${\theta _2} = {{\text{T}}_2}$

$\dfrac{{{\theta _1}}}{{{t_1}}} = \dfrac{{{K_1}{\pi _2}^2\left( {{T_1} - {T_2}} \right)}}{{{1_1}}}$  …….(1)

$\dfrac{{{\theta _2}}}{{{{\text{t}}_2}}} = \dfrac{{{{\text{K}}_2}\pi {\text{r}}_2^2\left( {\;{{\text{T}}_1} - {{\text{T}}_2}} \right)}}{{{1_2}}}$ …….(2)

Now, Divide equation (1) by (2)

$\dfrac{{{\theta _1}}}{{{{\text{t}}_1}}}{\text{X}}\dfrac{{{{\text{t}}_2}}}{{{\theta _2}}} = \dfrac{{{{\text{K}}_1}\left( {{\pi _1}^2} \right)\left( {{\theta _1} - {\theta _2}} \right)}}{{{{\text{K}}_2}\left( {\pi {\text{t}}{{\text{r}}_2}^2} \right)\left( {{\theta _1} - {\theta _2}} \right)}}{\text{X}}\dfrac{{{1_2}}}{{{{\text{l}}_1}}}$

Since,

$\dfrac{{{\theta _2}}}{{{t_2}}} = 4,\dfrac{{{t_2}}}{{{\theta _2}}} = \dfrac{1}{4};\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{1}{2}{\left( {\dfrac{{{r_1}}}{{{r_2}}}} \right)^2} = \dfrac{1}{4}$

$\dfrac{{{1_1}}}{{{1_2}}} = \dfrac{1}{2};\dfrac{{{1_2}}}{{{1_1}}} = \dfrac{2}{1}$

$\dfrac{{{\theta _1}}}{{{t_1}}} \times \dfrac{1}{4} = \dfrac{1}{2} \times {\left( {\dfrac{1}{2}} \right)^2} \times \left( {\dfrac{1}{2}} \right)$

$\dfrac{{{\theta _1}}}{{{t_1}}} \times \dfrac{Y}{{{A^\prime }}} = \dfrac{\gamma }{{{2^\prime }}} \times {A^\prime } \times 2$

$\dfrac{{{\theta _1}}}{{{t_1}}} = 1{\text{cal}}/{\text{sec}}$

32. What are thermal radiation? Write its properties of thermal radiation?

Ans: Thermal radiation is the radiant energy emitted by a body purely as a result of its temperature.

Thermal radiation has the following properties:

1) it travels through vacuum

2) it obeys refraction laws

3) it can be refracted

4) it travels at the speed of light

5) it does not heat the medium through which it

6) They exhibit phenomena of interference, diffraction and polarization.

33. An indirectly heated filament is radiating maximum energy of wavelength $2.16 \times {10^ - }$$^7\;{\text{m}}$. Find the net amount of heat energy lost per second per unit area, the temperature of surrounding air is ${13^0}{\mathbf{C}}$. Given ${\mathbf{b}} = 2.88 \times {10^{ - 3}}{\text{mk}},\sigma  = 5.77 \times {10^{ - 8}}\;{\text{J}}|{\mathbf{s}}|{{\mathbf{m}}^2}\mid {{\mathbf{k}}^4}$ ?

Ans: By using Wien's Law: -

The product of wavelength $(\lambda m)$ at which maximum energy is emitted and the absolute temperature (T) of the black body is always constant.

i.e., $\lambda m\;{\text{T}} = $ constant $ = {\text{b}} \to (1)$

${\text{b}} = $ Wien's constant $ = 2.9 \times {10^{ - 3}}{\text{mK}}$

Now, $\lambda {\text{m}} = 2.16 \times {10^{ - 7}}\;{\text{m}}$

${\text{T}} = $ Temperature of filament

So, ${\text{T}} = \dfrac{{\text{b}}}{{\lambda {\text{m}}}}({\text{by}}$ ……(1)

$T = \dfrac{{2.9 \times {{10}^{ - 3}}}}{{2.16 \times {{10}^{ - 7}}}}$

$T = \dfrac{{2.9 \times {{10}^{ - 3 + 7}}}}{{2.16}}$

$T = \dfrac{{29 \times {{10}^5}}}{{216}}$

${\text{T}} = 13333.3\;{\text{K}}$

Now, Temperature of surrounding, To $ = 13 + 273 = 286\;{\text{K}}$.

Net amount of heat energy lost per second per unit area: -

$E = \sigma \left( {{T^4} - T{o^4}} \right) \Rightarrow $ By Stefan’s law:

$E = 5.77 \times {10^{ - 8}}\left[ {{{(13333.3)}^4} - {{(286)}^4}} \right]$

${\text{E}} = 1.824 \times {10^8}\;{\text{J}}/{\text{s}}/{{\text{m}}^2}$

34. Animals in the forest find shelter from cold in holes in the snow. Why?

Ans: Animals in the forest find shelter from cold in holes in the snow Because, snow traps air (whereas ice does not) and acts as a heat insulator, animals in the forest seek refuge from the cold in holes in the snow. As a result, the snow prevents heat from being transferred from the animal's body to the exterior.

35. A brass boiler has a base area of $0.15\;{{\text{m}}^2}$ and thickness $1.0\;{\text{cm}}$. It boils water at the r a t e ~ o f ~ 6 kg/min when placed on a gas stove, Estimate the temperature of the part of flame in contact with the boiler. Thermal conductivity of brass =109J/s/m/0C, heat of vaporization of water $ = 2256\;{\text{J/g}}$ ?

Ans: Given data:

Rate of boiling of water is $ = 6.0{\text{Kg}}/{\text{min}}$

$ = \dfrac{{6 \times {{10}^3}\;{\text{g}}}}{{60{\text{sec}}}}$

$ = 100\;{\text{g}}/{\text{s}}$

$\therefore $ Rate at which heat is supplied by the flame to water is :-

${\text{m}} = $ Rate of boiling of water

${\text{L}}$ = heat of vaporization of water

$\theta  = {\text{mL}}$$ = \dfrac{{100g}}{s} \times \dfrac{{2256J}}{g}$

Θ = 225 600J/s

Now, ${{\text{T}}_2} = $ Temperature of cold junction $ = {100^0}{\text{C}}$

$\theta  = \dfrac{{{\text{KA}}\left( {{{\text{T}}_1} - {{\text{T}}_2}} \right){\text{x}}}}{{\text{t}}}$

$\theta  = $ heat flow

$A = $ Area of cross - section

${{\text{T}}_1} = $ Temperature of hot junction

${{\text{T}}_2} = $ Temperature of cold junction

${\text{t}} = $ time

${\text{x}} = $ Distance ${\text{b}}/{\text{w}}$ hot and cold junction

$225600 = \dfrac{{{\text{KA}}\left( {{{\text{T}}_1} - {{\text{T}}_2}} \right){\text{x}}}}{{\text{t}}}$

$\left( {{{\text{T}}_1} - {{\text{T}}_2}} \right) = \dfrac{{225600 \times {\text{x}}}}{{{\text{KAt}}}}$

Now, ${\text{x}} = 1.0\;{\text{cm}} = 1.0 \times {10^{ - 2}}\;{\text{m}}$

K=109 J/s/m/0C

${\text{A}} = 0.15\;{{\text{m}}^2}$

${\text{t}} = 1\;{\text{s}}$

${{\text{T}}_1} - {{\text{T}}_2} = \dfrac{{225600 \times 1.0 \times {{10}^{ - 2}}}}{{109 \times 0.15 \times 1}}$

${{\text{T}}_1} - {{\text{T}}_2} = {137.98^0}{\text{C}}$

${{\text{T}}_1} = {137.98^0}{\text{C}} + {{\text{T}}_2}$

${{\text{T}}_1} = 137.98 + 100$

${{\text{T}}_1} = {237.98^0}{\text{C}}$

36. How do you explain heating of rooms based on principle of convection?

Ans: The Principle of Convection is the process by which heat is transmitted from one point to another due to the movement of heated particles of the substance. During heating of the room by a heater, the air molecules in immediate contact with heater are heated up, they acquire sufficient energy and rise upward. The cool air particles near to the roof are dense and more down and in turn it is heated and moves upwards.

37. If for a gas, $\dfrac{R}{{{C_V}}} = 0.67$ then which gas is this: - monatomic, diatomic and tri atomic?

Ans: Since for an ideal gas, ${{\text{C}}_{\text{p}}} - {{\text{C}}_{\text{V}}} = {\text{R}} \to 1$ )

${{\text{C}}_{\text{P}}} = $ Specific heat at constant pressure

${{\text{C}}_{\text{V}}} = $ Specific heat at constant volume

${\text{R}} = $ Universal Gas Constant

And given $\dfrac{R}{{{C_V}}} = 0.67$

or $\dfrac{{{C_P} - {C_V}}}{{{C_V}}} = 0.67\quad (\because $ Using equation 1))

$\dfrac{{{C_P}}}{{{C_V}}} - 1 = 0.67$

$\dfrac{{{C_P}}}{{{C_V}}} = 1 + 0.67$

$\dfrac{{{C_P}}}{{{C_V}}} = 1.67$

And we know, that $\dfrac{{{C_P}}}{{{C_V}}} = 1.67$ is for monatomic gas; So, the gas is monatomic in question.

38. A $50\;{\text{g}}$ lead bullet, specific heat 0.02 Cal ${\text{/g}}{{\text{/}}^0}{\text{C}}$ is initially at ${30^0}{\text{C}}$. It is fixed vertically upward with a speed of $840\;{\text{m/s}}$ and on returning to the starting level strikes a cake of ice at ${0^0}{\mathbf{C}}$. How much ice is melted? Assume that all energy is spent in melting ice only?

Ans: Given Data: 

Speed of bullet hitting the ice $ = {\text{V}} = 840\;{\text{m/s}}$

Heat produced due to kinetic energy of the bullet: - $ = \dfrac{1}{2}m{V^2}$

Now, ${\text{m}} = $ Mass of bullet $ = 50\;{\text{g}} = \left( {50 \times {{10}^{ - 3}}} \right){\text{Kg}}$

Hence $ \Rightarrow \dfrac{1}{2}m{V^2} = \dfrac{1}{2} \times \left( {50 \times {{10}^{ - 3}}} \right) \times {(840)^2}$

$ = \dfrac{1}{2} \times 50 \times {10^{ - 3}} \times 705600$

$ = 17640\;{\text{J}}$

$ = \dfrac{{17640}}{{4.2}}{\text{Cal}}[\because $ To convert ${\text{J}} \to {\text{Cal}}$ we divide by 4.2]

$\left. {\dfrac{1}{2}m{V^2} = 4200{\text{Cal}} \to 1} \right)$

Now, heat given by bullet due to temperature difference $ = {\text{m}}$ c $\left( {{Q_2} - {Q_1}} \right)$

$ = 50 \times 0.02(30 - 0)$

$ = 30{\text{Cal}} \to 2$ )

From 1) & 2)

${\text{m}}$ = Mass of bullet

${\text{c}} = $ Specific heat of bullet

${{\text{Q}}_2} = $ Initial Temperature

${{\text{Q}}_1} = $ Final Temperature

Total heat given by bullet $ = 4200 + 30 = 4230{\text{Cal}}$.

Now, entire heat of bullet is used in melting the ice only, let ${\text{M}} = $ Mass of Ice that melted

${\text{L}} = $ Latent heat of ice

Hence $m \times L = 4230$

$m = \dfrac{{4230}}{L} = \dfrac{{4230}}{{80}}$

$m = 52.88g$

39. A gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature ${\text{T}}$. If we neglect all vibration modes, find the total energy of the system?

Ans: Let us consider:

${{\text{N}}_{\text{A}}} = $ Avogadro's Number

No. of degrees of freedom of ${{\text{O}}_2}$ molecule (diatomic) $ = 5$

No. of degrees of freedom of 2 moles of oxygen $ = 2\;{{\text{N}}_{\text{A}}} \times 5 = 10\;{{\text{N}}_{\text{A}}}$

No. of degrees of freedom of 4 moles of argon (monatomic) $ = 4\;{{\text{N}}_{\text{A}}} \times 3$

$ = 12\;{{\text{N}}_{\text{A}}}(\because 3 = $ degrees of freedom

Total degrees of freedom of mixture $ = 10\;{{\text{N}}_{\text{A}}} + 12\;{{\text{N}}_{\text{A}}} = 22\;{{\text{N}}_{\text{A}}} \to 1$ )

Energy associated with each degree of freedom $\mid $ molecule $ = \dfrac{1}{2}KT$

Total energy of mixture $ = 22\;{{\text{N}}_{\text{A}}} \times \dfrac{1}{2}KT$ ( $\because $ Using equation1)

$ = 11K\;{{\text{N}}_{\text{A}}}{\text{T}}$

$ = 11{\text{RT}}\left( {K{N_A} = R} \right)$

40. Show that ${C_P} - {C_V} = R$ Where $\left[ {{C_P} = } \right.$ specific heat at constant pressure; ${C_V} = $ specific heat at constant volume and ${\text{R}} = $ Universal Gas constant] for an ideal gas?

Ans: Let first heat the gas at constant volume and temperature increases by $\Delta T$, So, $\left. {\Delta Q = {C_V}\Delta T \to 1} \right)$

The complete heat given is used to raise the internal energy and hence the temperature of the gas, according to the law of conservation of energy, because the volume remains the same and no work is done to heat the gas. Now, $CV\Delta T = \Delta U$

$\therefore \Delta {\text{U}} = $ increase in the internal energy of the gas Let heat the gas at constant pressure and if the temperature of the gas increases by $\Delta {\text{T}}$ but here external work is done to expand the gas hence

$\Delta {{\text{Q}}^1} = \Delta {\text{U}} + \Delta {\text{W}}$

${{\text{C}}_{\text{p}}}\Delta {\text{T}} = {{\text{C}}_{\text{v}}}\Delta {\text{T}} + \Delta {\text{W}}({\text{Q}}$ from equation 1$\left. ) \right)$

But $\Delta W = P\Delta V,{\text{sO}}$

$\left. {{C_P}\Delta T = {C_V}\Delta T + P\Delta V \to 2} \right)$

Now, form ideal gas equation: 

$PV = RT \to 3)$ or ${\text{P}}(V + \Delta V) = R(T + \Delta T) \to 4)$

Subtracting equation 3) from equation 4)

$P\Delta V = R\Delta T$

Put $P\Delta V = R\Delta T$ in equation 2)

${C_P}\Delta T = {C_V}\Delta T + P\Delta V$

${C_P}\Delta T = {C_V}\Delta T + R\Delta T$

${C_P} = {C_V} + R$

or ${C_P} - {C_V} = R$

41. How do you justify that when a body is being heated at melting point, the temperature remains Constant?

Ans: When a body is heated below the melting point, the heat increases the molecules' potential as well as their kinetic energy. The temperature rises because to an increase in the kinetic energy of the mole clues. However, at melting point, heat is lost and only the potential energy of molecules is increased, therefore the temperature remains constant.

42. Draw and explain a P - T diagram for water showing different phases?

Ans: P - T diagram for water showing different phases is shown below:

P- Pressure

T- Temperature

1) The $1 - {\text{V}}$ curve represent those points where the liquid and vapour phases are in equilibrium.

2) The s - l curve represent the points where the solid and liquid phases exist in equilibrium.

3) The ${\text{s}} - {\text{v}}$ is the sublimation curve where a solid changes into vapour phase without passing through the liquid stage

4) Triple point  Intersection of three curves is the triple point. It represents a unique temperature and pressure and it is only at this point that the three phases can exist together in equilibrium.

43. From what height should a piece of ice fall so that it completely melts? Only one quarter of heat produced is absorbed by the ice. Given latent heat of ice is $3.4 \times {10^5}\;{\text{J}}\mid $ ${\text{Kg}}$ and acceleration due to gravity, ${\text{g}} = 10\;{\text{m}}\mid {{\text{s}}^2}$ ?

Ans: Let the Given,

${\text{m}} = $ Mass of piece of ice

${\text{h}}$ = height from which it falls.

$\therefore $ Loss of Potential energy $ = {\text{mgh}}$

The Potential energy of ice is converted into heat.

Since the ice absorbs only one - quarter of this,

$\therefore $ Heat absorbed by ice, $Q = \dfrac{1}{4}mgh \to 1$ )

If L Joules / Kg is the latent heat of ice, then

$Q = mL \to 2)$

Equating 1) & 2) for Q

$\dfrac{1}{4}pgh = m2$

$h = \dfrac{{4L}}{g}$

$h = \dfrac{{4 \times \left( {3.4 \times {{10}^5}} \right)}}{{10}}$

$h = 136 \times {10^3}\;{\text{m}}$

$h = 136{\text{Km}}$

44. A gas can have any value of specific heat depending upon how heating is carried out. Explain?

Ans: Let us consider, ${\text{m}}$ = Mass of gas

$Q = $ heat supplied

$\Delta T = $ Change in temperature

then specific heat of gas, $C = \dfrac{Q}{{m\Delta T}}$

1) Let gas is compressed suddenly, so no heat is supplied from outside (i.e., $Q = 0$ ) but the temperature of the gas in the gas increases due to compression,

$C = \dfrac{Q}{{m\Delta T}} = 0$

2) Let the gas is heated in a way that the temperature is constant $(\Delta {\text{T}} = 0)$ then,

$C = \dfrac{Q}{{m\Delta T}} = \dfrac{Q}{{mXo}} = \alpha $

Hence, depending upon conditions of heating. The value of ${\text{C}}$ will be different.

45. A $0.20{\text{Kg}}$ aluminium block at ${80^0}{\text{C}}$ is dropped in a copper calorimeter of mass $0.05{\text{Kg}}$ containing $200\;{\text{c}}{{\text{m}}^3}$ of ethyl alcohol at ${20^0}{\text{C}}$. What is the final temperature of the mixture? Given Density of ethyl alcohol $ = 0.81\;{\text{g/c}}{{\text{m}}^3};$ specific heat of ethyl alcohol = 0.6 Cal ${\text{/g}}{{\text{/}}^0}{\text{C}};$ specific heat of copper $ = 0.094{\text{cal/g}}{{\text{/}}^0}{\text{C}}$, specific heat of ${\text{Al}} = 0.22{\text{cal/g}}$$^0{\text{C}}?$

Ans: Let ${\theta ^0}{\text{C}} = $ final temperature of the mixture.

Mass of ethyl alcohol = volume $ \times $ Density

$ = 200 \times 0.81$

$ = 162\;{\text{g}}$

Heat lost by Aluminium block = Mass ${\text{X}}$ specific heat ${\text{X}}$ fall in temperature

$ = \left( {0.20 \times {{10}^3}} \right) \times 0.22 \times (80 - \theta )$

$ = 20 \times 22 \times {10^{ - 4}} \times {10^3}(80 - \theta )$

$ = 440 \times {10^{ - 1}}(80 - \theta )$

$ = 44(80 - \theta ) \to 1)$

Heat gained by the ethyl alcohol and calorimeter = (Mass of ethyl alcohol $ \times $ specific heat x change in Temperature) + Mass of copper calorimeter $ \times $ specific heat ${\text{X}}$ change in

Temperature

$ = [162 \times 0.6 \times (\theta  - 20)] + \left[ {0.05 \times {{10}^3} \times 0.094 \times (\theta  - 20)} \right]$

$ = 101.9(\theta  - 20) \to 2)$

But Heat gained =Heat Lost

So, from equation 1) & 2)

44(80-θ) =101.9(θ-20)

$ \Rightarrow 3520 - 44\theta  = 101.9\theta  - 2038$

$3520 + 2038 = 101.9\theta  + 44\theta $

$5558 = 145.9\theta $

$\theta  = \dfrac{{5558}}{{145.9}}$

$\theta  = {38.1^0}{\text{C}}$

46. Why is there a difference in the specific heat curve as given belongs petit law and the experimental result at low temperatures?

Ans: Now, from Dulong & Petit law, the specific heat is independent of temperature but it is experimentally seen that specific heat at lower temperatures is directly proportional to the cube of temperatures. The above dependence is because of the fact that the particles in the crystal oscillate as if they are coupled Quantum Harmonic

47. Specific heat of Argon at constant Pressure is $0.125{\text{cal/g/K}}$ and at constant volume is 0.075 Cal /g/ K. Calculate the density of argon at N.T.P. Given that ${\mathbf{J}} = 4.2\;{\text{J}}$ Cal?

Ans: Given Data:

Specific heat at constant and Pressure, ${{\text{C}}_{\text{P}}} = 0.125{\text{cal}}|{\text{g}}|{\text{K}}$${{\text{C}}_{\text{P}}} = 0.125 \times 4.2 \times 1000\;{\text{J/Kg/K}}$

$\left. {{{\text{C}}_{\text{P}}} = 525\;{\text{J/Kg/K}} \to 1} \right)$

Specific heat at constant volume, ${{\text{C}}_{\text{V}}} = 0.075{\text{cal/g/K}}$

${C_V} = 0.075 \times 4.2 \times 1000$

${C_V} = 315J/Kg/K$

The gas constant, ${\text{r}}$ for ${\text{Ikg}}$ of gas is given by: -

$r = {C_P} - {C_V} = 525 - 315 = 210J/Kg/K$

Normal pressure $ = {\text{P}} = {\text{hPg}} = 0.76 \times 13600 \times 9.8 = 101292.8\;{\text{N/}}{{\text{m}}^2}$

Normal Temperature $ = {\text{T}} = 273\;{\text{K}}$.

Suppose ${\text{V}} = $ Volume of argon in ${{\text{m}}^3}$ at N. T. P.

$PV = {\text{nrT}}$

for ${\text{n}} = 1$ mole

$\dfrac{{PV}}{T} = r$${\text{V}} = \dfrac{{rT}}{P} = \dfrac{{210X273}}{{101292.8}} = 0.566\;{{\text{m}}^3}$

$\therefore $ Density of Argon, $P = \dfrac{{{\text{ Mass }}}}{{{\text{ Volume }}}} = \dfrac{1}{{0.566}} = 1.8{\text{Kg/}}{{\text{m}}^3}$.

48. How is heat loss reduced in Calorimeter?

Ans:1) The Calorimeter's inner and outer surfaces are polished to prevent heat loss owing to radiation.

2) By covering the area between the calorimeter and the insulating jacket with a poor heat conductor, heat loss owing to conduction is decreased.

3) To prevent heat loss due to convection, an insulating lid is used.

49. What is critical temperature? How will you differentiate between a gas and a vapour depending on critical temperature?

Ans: The temperature above which a gas cannot liquefy, regardless of pressure, is referred to as critical temperature. If the temperature of a substance is higher than the critical temperature, it is said to be in the gaseous state. The substance is in the vapour stage if it is below the critical temperature.

50. If for hydrogen ${\text{CP}} - {\text{CV}} = {\text{a}}$ and for oxygen ${\text{CP}} - {\text{CV}} = {\mathbf{b}}$ where CP & CV refer to specific heat at constant pressure and volume then what is the relation between a and ${\mathbf{b}}$ ?

Ans: For ${{\text{H}}_2},{{\text{C}}_{\text{P}}} - {{\text{C}}_{\text{V}}} = {\text{a}}$

${{\text{C}}_{\text{p}}} = $ Specific heat at constant pressure

${{\text{C}}_{\text{V}}} = $ Specific heat at constant Volume

For ${{\text{O}}_2} = {{\text{C}}_{\text{P}}} - {{\text{C}}_{\text{V}}} = {\text{b}}$

And ${\text{r}} = \dfrac{R}{{MJ}}$

${\text{M}} = $ Molecular weight

I = Mechanic Cal equivalent of heat

Now, we know that, ${{\text{C}}_{\text{P}}} - {{\text{C}}_{\text{V}}} = {\text{r}}$

${C_P} - {C_V} = \dfrac{R}{{MJ}}$

So, for ${H_2} \Rightarrow {C_P} - {C_V} = a = \dfrac{R}{{2J}}$

$\left. {{M_{H2}} = 2\mid {C_P} - {C_V} = a = \dfrac{R}{{2J}} \to 1} \right)$

For ${{\text{O}}_2} \Rightarrow {{\text{C}}_{\text{p}}} - {{\text{C}}_{\text{V}}} = {\text{b}} = \dfrac{R}{{32\;{\text{J}}}} \to 2$ )

from equation 1)

$2{\text{a}} = \dfrac{R}{J}$

from equation 2)

$32\;{\text{b}} = \dfrac{R}{J}$

Equating above equations for $\dfrac{R}{J}: \to $

$2a = 32b$

$a = 16b$

51. A ball is dropped on a floor from a height of $2\;{\text{cm}}$. After the collision, it rises up to a height of $1.5\;{\text{m}}$. Assuming that $40\% $ of mechanical energy lost goes to thermal energy into the ball. Calculate the rise in temperature of the ball in the collision. Specific heat capacity of the ball is $800\;{\text{J}}/{\text{k}}$. Take ${\text{g}} = {\mathbf{10}}{\text{m}}/{{\text{s}}^2}$

Ans: Given Data:

Initial height $ = {{\text{h}}_1} = 2\;{\text{m}}$

Final height $ = {{\text{h}}_2} = 1.5\;{\text{m}}$

Since potential energy = mechanical energy for a body at rest as ${\text{K}}.{\text{E}} = 0$

Mechanical energy lost $ = \left| {mg\left( {{h_1} - {h_2}} \right)} \right|$

$ = |1 \times 10(105 - 2)|$

$ = |10 \times (.5)|$

$ = 5\;{\text{J}}$

Now (mechanical energy lost) $ \times 40\%  = $ heat gained by ball

$\dfrac{{40}}{{100}} \times 5 = {\text{cm}}\Delta T\quad {\text{C}} = $ specific heat of ball

$\dfrac{{40}}{{100}} \times 5 = 800 \times 1 \times \Delta T\;{\text{m}} = $ Mass of ball $ = 1\;{\text{kg}}$

$\dfrac{1}{{400}} = \Delta T\Delta {\text{T}} = 2.5 \times {10^{ - 3}}{\text{CC}}$

Marks Questions Part 3

52. A thermometer has wrong calibration. It reads the melting point of ice as $ - {10^0}{\text{C}}$. It reads ${60^0}{\text{C}}$ in place of ${50^0}{\text{C}}$. What is the temperature of boiling point of water on the scale?

Ans: Given Data:

Lower fixed point on the wrong scale $ =  - {10^0}{\text{C}}$.

Let ' $^\prime n$ ' = no. divisions between upper and lower fixed points on this scale. If $Q = $ reading on his scale, then $\dfrac{{C - O}}{{100}} = \dfrac{{Q - ( - 10)}}{n}$

Now, ${\text{C}} = $ Incorrect Reading $ = {60^0}{\text{C}}$

2 = Correct Reading $ = {50^0}{\text{C}}$

so, $\dfrac{{50 - 0}}{{100}} = \dfrac{{60 - ( - 10)}}{n}$

$\dfrac{{50}}{{100}} = \dfrac{{70}}{n}$

$n = 70 \times \dfrac{{100}}{{50}}$

$1 = 140$

Now, $\dfrac{{C - O}}{{100}} = \dfrac{{Q - ( - 10)}}{{140}}$

On, the Celsius scale, Boiling point of water is ${100^0}{\text{C}}$

So, $\dfrac{{100 - 0}}{{100}} = \dfrac{{Q + 10}}{{140}}$

$Q = 140 - 10$

${\text{Q}} = {130^0 }{\text{C}}$

53. Write the advantages and disadvantages of platinum resistance thermometer?

Ans:
Advantages of Platinum Resistance thermometer: -

1) High accuracy of measurement

2) Measurements of temperature can be made over a wide range of temperature i.e., from ${260^0}{\text{C}}$ to ${1200^0}{\text{C}}$.

Disadvantages of Platinum Resistance thermometer: -

1) High Cost

2) Requires additional equipment such as bridge circuit, Power supply etc.

54. If the volume of block of metal changes by $0.12\% $ when it is heated through 200C. What is the co-efficient of linear expansion of the metal?

Ans: The co-efficient of cubical expansion y of the metal is given by: -

$Y = \dfrac{{\Delta V}}{V} \times \dfrac{1}{{\Delta T}}$

Here, $\dfrac{{\Delta V}}{V} = \dfrac{{0.12}}{{100}}$

$\Delta T = {20^0}{\text{C}}$

$Y = \dfrac{{0.12}}{{100}} \times \dfrac{1}{{20}}$

$Y = 6 \times {10^{ - 5}}{\text{C}}$

Co-efficient of linear expansion of the metal is: -

$\alpha  = \dfrac{Y}{3} = \dfrac{{6.0 \times {{10}^{ - 5}}}}{3}$

$\alpha  = 2.0 \times {10^{ - 3}}{\text{C}}$

55. The density of a solid at ${0^0}{\text{C}}$ and ${500^0}{\text{C}}$ is in the ratio 1.027: 1. Find the co-efficient of linear expansion of the solid?

Ans: Given Data:

Density at ${500^0}{\text{C}} = {{\text{S}}_{500}}$

Now, ${{\text{S}}_0} = {{\text{S}}_{500}}(1 + Y\Delta T)$

Were, ${\text{Y}} = $ Co-efficient of volume expansion

$\Delta {\text{T}} = $ Change in temperature

$\because \dfrac{{SO}}{{{S_{500}}}} = \dfrac{{1.027}}{1}$

$\Delta {\text{T}} = $ Change in temperature

$\Delta {\text{T}} = $ Final Temperature - Initial temperature

$\Delta {\text{T}} = 500 - {0^0}{\text{C}}$

$\Delta {\text{T}} = {500^0}{\text{C}}$

Or $1.027 = 1 \times (1 + Y\Delta T)$

$1.027 = 1 + Y\Delta T$

$1.027 - 1 = Y\Delta T$

$0.027 = Y\Delta T$

$\dfrac{{0.027}}{{500}} = Y$

$Y = 54 \times {10^{ - 5}}{\text{C}}$

Now, Co-efficient of linear expansion (a) is related to co-efficient of volume expansion (Y) as

$\alpha  = \dfrac{Y}{3}$

$\alpha  = \dfrac{{54 \times {{10}^{ - 6}}}}{3}$

$\alpha  = 18 \times {10^{ - 6}}{\text{C}}$

56. If one Mole of a monatomic gas is mixed with 3 moles of a diatomic gas. What is the molecular specific heat of the mixture at constant volume?

Ans: For, a monatomic gas, Specific heat at consent volume $ = {{\text{C}}_{{\text{V}}1}} = \dfrac{3}{2}R;{\text{R}} = $ Universal Gas Constant

No. of moles of monatomic gas $ = {{\text{n}}_1} = 1\;{\text{mole}}$

No. of moles of diatomic gas $ = {{\text{n}}_2} = 3$ moles.

For, diatomic gas, specific heat at constant volume ${C_{V2}} = \dfrac{5}{2}R$.

Applying, conservation of energy.

Let ${{\text{C}}_{\text{V}}} = $ Specific heat of the mixture;

${C_V} = \dfrac{{{n_1}C{v_1} + {n_2}C{v_2}}}{{{n_1} + {n_2}}}$

${C_V} = \dfrac{{1 \times \dfrac{3}{2}R + 3 \times \dfrac{5}{2}R}}{{1 + 3}}$

${C_V} = \dfrac{{\dfrac{3}{2}R + \dfrac{{15}}{2}R}}{4}$

${\text{R}} = $ Universal Gas constant

${C_V} = \dfrac{{18R}}{{2 \times 4}}$

${C_V} = \dfrac{{9R}}{4}$

${C_V} = \dfrac{9}{4} \times 8.31$

${C_V} = 18.7J/\operatorname{mol} {/^0}K$

Q57. Calculate the difference between two principal specific heats of 1g of helium gas at N. T. P. Given Molecular weight of Helium = 4 and J = 4.186 J/Cal and Universal Gas constant, R = 8.314J mole/K?

Ans: Given Data:

Molecular weight of Helium $ = {\text{M}} = 4$

Universal Gas Constant, ${\text{R}} = 8.31\;{\text{J}}\mid $ mole $\mid {\text{K}}$

${{\text{C}}_{\text{P}}} = $ specific heat at constant Pressure

${{\text{C}}_{\text{V}}} = $ specific heat at constant Volume

Now, ${C_P} - {C_V} = \dfrac{r}{J}$ for 1 mole of gas.

${C_P} - {C_V} = \dfrac{R}{{MJ}}$

Where ${\text{R}} = $ Universal Gas Constant $ = 8.31\;{\text{J/mole/k}}$

${\text{J}} = 4.186\;{\text{J/cal}}$

${\text{M}} = $ Molecular weight of Helium $ = 4$

${C_P} - {C_V} = \dfrac{{8.31}}{{4 \times 4.186}}$

${C_P} - {C_V} = 0.496{\text{cal/}}g/K$

58. Why does heat flow from a body at higher temperature to a body at lower temperature?

Ans: When a body with a higher temperature comes into touch with a body with a lower temperature, molecules with a greater kinetic energy that come into contact with less energetic molecules give up some of their kinetic energy to the less energetic molecules.

59. A one litre flask contains some mercury. IT is found that at different temperatures, then volume of air inside the flask remains the same. What is the volume of mercury in the flask? Given the co-efficient of linear expansion of glass $ = 9 \times {10^{ - 6}}{/^0}{\text{C}}$ and coefficient of volume expansion of mercury $ = 1.8 \times {10^{ - 4}}/$$^0{\text{C}}$

Ans: It is assumed that the volume of air in the flask remains constant regardless of temperature. Only when the expansion of glass equals the expansion of mercury is this possible.

Co-efficient of cubical expansion of glass is: -

${\gamma _g} = 3{\alpha _g} = 3 \times 9 \times {10^{ - 6}}$

$ = 27 \times {10^{ - 6}}{/^0}{\text{C}}$

Co-efficient of cubical expansion of mercury is:

γm=1.8×10-4/C (Given)

Volume of flask, ${\text{V}} = 1$ litre $ = 1000\;{\text{c}}{{\text{m}}^3}$.

Let ${{\text{V}}_{\text{m}}}{\text{C}}{{\text{m}}^3}$ be the volume of mercury in the flask.

Expansion of flask = Expansion of Mercury

$CX{\gamma _g} \times t = {V_m}X{\gamma _m} \times t$

$\therefore $ Volume of Mercury, ${V_m} = \dfrac{{V \times \gamma g}}{{{\gamma _m}}}$

${V_m} = \dfrac{{1000 \times 27 \times {{10}^{ - 5}}}}{{1.8 \times {{10}^{ - 4}}}} = 150\;{\text{c}}{{\text{m}}^3}$

60. A refrigerator is to maintain eatables kept inside at ${9^0}{\text{C}}$. If room temperature is ${36^0}$ C, calculate the coefficient of performance.

Ans: Given Data:

Temperature inside the refrigerator, ${T_1} = {9^0}{\text{C}} = 282\;{\text{K}}$

Room temperature, ${T_2} = {36^0}{\text{C}} = 309\;{\text{K}}$

Coefficient of performance $ = \dfrac{{{T_1}}}{{{T_2} - {T_1}}}$

$ = \dfrac{{282}}{{309 - 282}}$

$ = 10.44$

Therefore, the coefficient of performance of the given refrigerator is 10.44.

61. A steam engine delivers $5.4 \times {10^8}\;{\text{J}}$ of work per minute and services $3.6 \times {10^9}\;{\text{J}}$ of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?

Ans: Given data:

Work done by the steam engine per minute, $W = 5.4 \times {10^8}\;{\text{J}}$

Heat supplied from the boiler, $H = 3.6 \times {10^9}{\mathbf{J}}$

Efficiency of the engine $ = \dfrac{{{\text{ Outputenergy }}}}{{{\text{ Input energy }}}}$

$\therefore \eta  = \dfrac{W}{H} = \dfrac{{5.4 \times {{10}^8}}}{{3.6 \times {{10}^9}}} = 0.15$

Hence, the percentage efficiency of the engine is $15\% $.

Amount of heat wasted $ = 3.6 \times {10^9} - 5.4 \times {10^8}$

$ = 30.6 \times {10^8} = 3.6 \times {10^9}\;{\text{J}}$

Therefore, the amount of heat wasted per minute is $3.6 \times {10^9}{\mathbf{J}}$.

62. A thermodynamic system is taken from an original state to an intermediate state by the linear process shown in Fig. (12.13)

Its volume is then reduced to the original value from ${\mathbf{E}}$ to ${\mathbf{F}}$ by an isobaric process. Calculate the total work done by the gas from ${\text{D}}$ to ${\text{E}}$ to ${\text{F}}$

Ans: Total work done by the gas from ${\text{D}}$ to ${\text{E}}$ to ${\text{F}} = $ Area of $\vartriangle {\text{DEF}}$

Area of $\Delta {\text{DEF}} = \dfrac{1}{2}DE \times EF$

Were,

${\text{DF}} = $ Change in pressure

$ = 600\;{\text{N}}/{{\text{m}}^2} - 300\;{\text{N}}/{{\text{m}}^2}$

$ = 300\;{\text{N}}/{{\text{m}}^2}$

${\text{FE}} = $ Change in volume

$ = 5.0\;{{\text{m}}^3} - 2.0\;{{\text{m}}^3} = 3.0\;{\text{m}}3$

Area of $\vartriangle {\text{DEF}} = \dfrac{1}{2} \times 300 \times 3 = 450\;{\text{J}}$

Therefore, the total work done by the gas from $D$ to $E$ to $F$ is $450\;{\text{J}}$.

3 Marks Questions

1. Calculate the work done during the isothermal Process?

Ans: Let an ideal gas is allowed to expand very slowly at constant temperature. Let the expands from state ${\text{A}}\left( {{{\text{P}}_1},{{\text{v}}_1}} \right)$ to state B $\left( {{{\text{P}}_2},{{\text{v}}_2}} \right)$

The work by the gas in expanding from state ${\text{A}}$ to ${\text{B}}$ is

${\text{P}} = $ Pressure ${\text{V}} = $ Volume

$n = $ No. of moles ${\text{R}} = $ Universal Gas constant ${\text{T}} = $ Temperature

$W =  + \int_{{V_1}}^{{v_2}} P dV \to (1)$

For ideal gas, ${\text{PV}} = {\text{NRT}}$

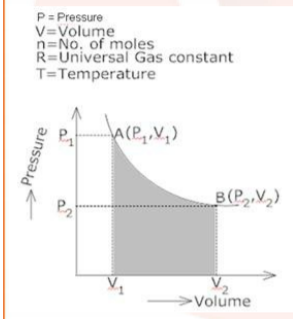
or ${\text{P}} = \dfrac{{nRT}}{V} \to (2)$

Use 2) in i)

${\text{W}} = \int_{{V_{\text{i}}}}^{{V_2}} {\dfrac{{nRT}}{V}} dV$

Since ${\text{n}},{\text{R}}$ and ${\text{T}}$ are constant so,

${\text{W}} = nRT\int_{{V_{\text{L}}}}^{{V_2}} {\dfrac{{dV}}{V}} \quad \left( {\because \int {\dfrac{{dn}}{n}}  = } \right.$ Logem)

W isothermal = nRT Loge V

${\text{W}}$ isothermal $ = nRT\left[ {{{\operatorname{LogeV} }_2} - {{\operatorname{LogeV} }_1}} \right]\left( {\because \operatorname{Logm}  - \log n = \log \dfrac{m}{n}} \right)$

W isothermal - nRT Loge $\dfrac{{{V_2}}}{{{V_1}}}$

W isothermal $ = 2.303$ nRT $\log 10\dfrac{{{V_2}}}{{{V_1}}}$ (Loge $ = 2.303$ Log10)

If ${\text{M}} = $ Molecular Mass of gas then for 1 gram of ideal gas,

W isothermal $ = 2.303\dfrac{{RT}}{M}\log 10\dfrac{{{V_2}}}{{{V_1}}}$

W isothermal $2.303{\text{rT}}\log 10\dfrac{{{V_2}}}{{{V_1}}}$

${\text{r}} = $ Gas constant for $1{\text{gm}}$ of an ideal gas,

Since ${{\text{P}}_1}\;{{\text{V}}_1} = {{\text{P}}_2}\;{{\text{V}}_2} \Rightarrow \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{{P_1}}}{{{P_2}}}$

So ${\text{W}}$ isothermal $ = 2.303{\text{rT}}\log 10\dfrac{{{P_1}}}{{{P_2}}}$

2. Five moles of an ideal gas are taken in a Carnot engine working between ${100^0}{\text{C}}$ and ${30^0}{\text{C}}$. The useful work done in 1 cycle is $420\;{\text{J}}$. Calculate the ratio of the volume of the gas at the end and beginning of the isothermal expansion?

Ans: Let be a given data:

High temperature, ${{\text{T}}_{\text{H}}} = {100^0}{\text{C}} = 100 + 273 = 373\;{\text{K}}$

Low temperature, ${{\text{T}}_{\text{L}}} = {30^0}{\text{C}}, = 30 + 273 = 303\;{\text{K}}$

Amount of the gas, ${\text{n}} = 5$ moles

Useful work done per cycle, ${\text{W}} = {{\text{Q}}_{\text{H}}} - {{\text{Q}}_{\text{L}}}$

Now, ${\text{W}} = 420\;{\text{J}}$

So, $\left. {{{\text{Q}}_{\text{H}}} - {{\text{Q}}_{\text{L}}} = 420\;{\text{J}} \to 1} \right)$

Now, $\dfrac{{{Q_H}}}{{{Q_L}}} = \dfrac{{{T_H}}}{{{T_L}}}$

$\dfrac{{{Q_H}}}{{{Q_L}}} = \dfrac{{373}}{{303}}$

Or ${{\text{Q}}_{\text{H}}} = \dfrac{{373}}{{303}}{{\text{Q}}_{\text{L}}}$ in equation 1)

$\dfrac{{373}}{{303}}{Q_L} - {Q_L} = 420\;{\text{J}}$

$\dfrac{{373{Q_L} - 303{Q_L}}}{{303}} = 420\;{\text{J}}$

$\dfrac{{70{Q_L}}}{{303}} = 420$

${Q_L} = \dfrac{{420X303}}{{70}}$

${\text{QL}} = 1818\;{\text{J}}$

or, ${{\text{Q}}_{\text{H}}} - {{\text{Q}}_{\text{L}}} = 420\;{\text{J}}$

${{\text{Q}}_{\text{H}}} - 1818 = 420\;{\text{J}}$

${{\text{Q}}_{\text{H}}} = 420 + 1818 = 2238\;{\text{J}}$

When the gas is carried through Carnot cycle, the heat absorbed ${{\text{Q}}_{\text{H}}}$ during isothermal

expansion is equal to the work done by gas.

${{\text{V}}_1}$ - Initial Volume

${{\text{V}}_2} = $ Final Volume,

In isothermal expansion,

${\text{QH}} = 2.303{\text{nR}}{{\text{T}}_{\text{H}}}\log 10\dfrac{{{V_2}}}{{{V_1}}}$

$2238 = 2.303 \times 5 \times 8.4 \times 373\log 10\dfrac{{{V_2}}}{{{V_1}}}$

$\log 10\dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{2238}}{{2.303 \times 5 \times 8.4 \times 373}}$

$\log 10\dfrac{{{V_2}}}{{{V_1}}} = 0.0620$

$\dfrac{{{V_2}}}{{{V_1}}} = 1.153$

3. Deduce the work done in the following complete cycle?

Ans:
1) Work done during the process from ${\text{A}}$ to ${\text{B}} = {{\text{W}}_{{\text{AB}}}}$

${{\text{w}}_{{\text{AB}}}} = $ area ABKLA ( $\therefore $ because area under ${\text{p}}$ -v curve gives work done)

= area of $\vartriangle {\text{ABC}} + $ area of rectangle

$ = \left( {\dfrac{1}{2} \times BC \times AC} \right) + (KL \times LC)$

${\text{BC}} = {\text{KL}} = 4 - 1 = 3{\text{l}} = 3{\text{x}}{10^{ - 3}}\;{{\text{m}}^3}$

${\text{AC}} = 4 - 2 = 2\;{\text{N/}}{{\text{m}}^2}$

LC $ = 2 - 0 = 2\;{\text{N/}}{{\text{m}}^2}$

${{\text{W}}_{{\text{AB}}}} = \left( {\dfrac{1}{2} \times 3 \times {{10}^{ - 3}} \times 2} \right) + \left( {3 \times {{10}^{ - 3}} \times 2} \right)$

$ = 3 \times {10^{ - 3}} + 6 \times {10^{ - 3}}$

${{\text{W}}_{{\text{AB}}}} = 9 \times {10^{ - 3}}\;{\text{J}}$

Since gas expands during this process, hence ${{\text{W}}_{{\text{AB}}}} = 9 \times {10^{ - 3}}\;{\text{J}}$

2) Work done during the process from B to C(compression) is ${{\text{W}}_{{\text{BC}}}} = $ -area BCLK

(- ve because gas compresses during BC)

$ =  - {\text{KL}} \times {\text{LC}}$

${{\text{W}}_{{\text{BC}}}} =  - 3 \times {10^{ - 3}} \times 2$

$ =  - 6 \times {10^{ - 3}}\;{\text{J}}$

3) Work done during the process from ${\text{C}}$ to ${\text{A}}: - $As there is no change in volume of gas in this process, ${{\text{W}}_{{\text{CA}}}} = 0$

So, net work done during the complete cycle $ = {{\text{W}}_{{\text{AB}}}} + {{\text{W}}_{{\text{BC}}}} + {{\text{W}}_{{\text{CA}}}}$

$ = 9 \times {10^{ - 3}} - 6 \times {10^{ - 3}} + 0$

Net work done $ = 3 \times {10^{ - 3}}\;{\text{J}}$

4. One kilogram molecule of a gas at 400k expands isothermally until its volume is doubled. Find the amount of work done and heat produced?

Ans: Let us consider,

Initial volume, ${{\text{V}}_1} = {\text{V}}$

Final volume, ${{\text{V}}_2} = 2\;{\text{V}}$

Initial temperature ${\text{T}} = 400{\text{k}}$

Find temperature $ = 400{\text{k}}(\therefore $ process is isothermal)

Gas constant, R=8.3kj/mole/K =8.3 × 10-3 J/mole/k done during is thermal process - ${\text{w}} = 2.3026{\text{RT}}\log 10\left( {\dfrac{{{V_2}}}{{{V_1}}}} \right)$

${\text{W}} = 2.3026 \times 8.3 \times {10^{ - 3}} \times 400 \times \log 10\left( {\dfrac{{2V}}{V}} \right)$

${\text{W}} = 2.3026 \times 8.3 \times {10^{ - 3}} \times 400 \times \log 10(2)$

${\text{W}} = 2.3016\;{\text{J}}$

If ${\text{H}}$ is the amount of heat produced than,

${\text{H}} = \dfrac{{\text{W}}}{{\text{J}}} = \dfrac{{2.3016}}{{4.2}} = 0.548C{\text{al}}$

5. Calculate difference in efficiency of a Carnot energy working between: -

1) 400K and 350K

2) 350K and 300K

Ans: Efficiency of heat engine $ = {\text{n}} = 1 - \dfrac{{{T_2}}}{{{T_1}}}$

${{\text{T}}_2} = $ final temperature

${{\text{T}}_1} = $ Initial temperature

1) 400K and 350K:

${{\text{T}}_2} = 350,\;{{\text{T}}_1} = 400$

${\text{n}} = 1 - \dfrac{{350}}{{400}}$

$ = \dfrac{{50}}{{400}}$

${{\text{n}}_1} = \dfrac{1}{8}$ or $\dfrac{{100\% }}{8} = 12.5\% $

2) 350K and 300K:

${{\text{T}}_2} = 300\;{\text{K}};{{\text{T}}_1} = 350\;{\text{K}}$

${{\text{n}}_1} = 1 - \dfrac{{{T_2}}}{{{T_1}}}$

$ = 1 - \dfrac{{300}}{{350}}$

$ = \dfrac{{50}}{{350}}$

${{\text{n}}_1} = \dfrac{1}{7} = \dfrac{{100\% }}{7} = 14.3\% $

Change in efficiency $ = {{\text{n}}_2} - {{\text{n}}_1} = 14.3\%  - 12.5\%  = 1.8\% $

6. How do you derive Newton's law of cooling from Stefan's law?

Ans: According to Newton's rule of cooling, the rate of heat loss of a liquid is exactly proportional to the temperature difference between the liquid and the surrounding, as long as the temperature difference is modest.

$E\alpha \left( {T - {T_0}} \right)$

Let a body be maintained at ${\text{TK}}$. Let ${{\text{T}}_0}$ be the temperature of the surroundings. Let ${\text{T}} \gg $ To. There will be loss of heat be the body

Acc. to Stefan's law, amount of heat energy lost per second per unit area of the body is:

$\sigma  = $ Stefan's constant

$\varepsilon  = $ Emissivity of the body and surroundings

${\text{E}} = \varepsilon \sigma \left( {{T^2} - T{o^2}} \right)\left( {{T^2} + T{o^2}} \right)$

$\left( {\because \left( {{a^4} - {b^4}} \right) = \left( {{a^2} - {b^2}} \right)\left( {{a^2} + {b^2}} \right)} \right.$

In case of Newton's cooling, ${\text{T}}$

${\text{E}} = \varepsilon \sigma \left( {T - {T_0}} \right)\left( {{T_0} + T} \right)\left( {T{O^2} + T{O^2}} \right)$

${\text{E}} = \varepsilon \sigma ({\text{T}} - {\text{T}}^\circ )4\;{\text{T}}_0^3$

$E = K\left( {T - {T_0}} \right)$

$K = 4\varepsilon \sigma T{o^3}$

Hence,  Hence the Newton's law of cooling

${\text{E}}\alpha \left( {T - {T_0}} \right)$

7. Define the terms reflectance, absorptance and transmittance. How are they related?

Ans:
1) Reflectance - Ratio of number of thermal radiations reflected by the body in a given time to total amount of thermal radiations incident on body It is represented by ${\text{r}},$

2) Absorptance - is the ratio of the amount of thermal to the total amount of thermal radiations incident on it.

3) Transmittance - This is the ratio of the total amount of thermal radiations incident on the body in a particular time to the total amount of thermal radiations transmitted by the body in that time. It is symbolised by the letter t. Let Amount of the radiation’s incident by the body in a given time.

${{\text{Q}}_1} = $ Number of thermal radiations reflected by the body in a given time.

${{\text{Q}}_2}$ - Number of thermal radiations absorbed by the body in a given time.

${{\text{Q}}_3} = $ Number of thermal radiations transmitted by the body in a given time,

$\therefore $ By definition,

$r = \dfrac{{{Q_1}}}{Q}$

$a = \dfrac{{{Q_2}}}{Q}$

$t = \dfrac{{{Q_3}}}{Q}$

New, $r + a + t = \dfrac{{{Q_1}}}{Q} + \dfrac{{{Q_2}}}{Q} + \dfrac{{{Q_3}}}{Q}$

${\text{R}} + {\text{a}} + {\text{t}} = \dfrac{{{Q_1} + {Q_2} + {Q_3}}}{Q}$

${\text{R}} + {\text{a}} + {\text{t}} = 1$

$\left( {\because {Q^1} + {Q_2} + {Q_3} = Q} \right)$

If ${\text{t}} = 0$

${\text{A}} = 1 - {\text{r}}$

that is good reflectors are bad absorbers.

8. If half mole of helium is contained in a container at S. T. P. How much heat energy is needed to double the pressure of the gas, keeping the volume of the gas constant? Given specific heat of gas $ = 3\;{\text{J}}/{\text{g/K}}$.

Ans: Number of moles of Helium gas $ = n = \dfrac{1}{2}$.

Specific heat of Helium gas $ = {C_V} = 3J/g/K$

Molecular weight $ = {\text{M}} = 4$

Temperature, ${{\text{T}}_1} = 273\;{\text{K}}$.

$\therefore $ Molar specific heat at constant volume $ = {{\text{C}}_{\text{V}}} = {{\text{M}}_{{\text{CV}}}}$

${{\text{C}}_{\text{V}}} = 4 \times 3$

${{\text{C}}_{\text{V}}} = 12\;{\text{J/mol/K}}$

Since, Volume is constant, ${\text{Pa}}$ T or $\dfrac{P}{T} = $ Constant

$\therefore \dfrac{{{P_2}}}{{{T_2}}} = \dfrac{{{P_1}}}{{{T_1}}}\quad {\text{P}} = $ Pressure; ${\text{T}} = $ Temperature

Or $\dfrac{{{P_2}}}{{{P_1}}} = \dfrac{{{T_2}}}{{{T_1}}}$

${{\text{P}}_2} = $ Final Pressure $ = 2{\text{P}}$

${{\text{P}}_1} = $ Initial Pressure $ = {\text{P}}$

$\dfrac{{2P}}{P} = \dfrac{{{T_2}}}{{{T_1}}}$

$\dfrac{{{T_2}}}{{{T_1}}} = 2$

${T_2} = 2{T_1}$

${T_2} = 2X273$

${T_2} = 546K$

$\Delta T = {T_2} - {T_1} = 546 - 273 = 273K$

Now, Heat required, $ = Q = n{C_V}\Delta T$

$ = \dfrac{1}{2} \times 12 \times 273$

Heat required $ = 1638\;{\text{J}}$

9. Calculate the amount of heat necessary to raise the temperature of 2 moles of HE gasses from ${20^0}{\text{C}}$ to ${50^0}{\text{C}}$ using: -

1) Constant - Volume Process 2) Constant Pressure Process

Here for, He; ${{\text{C}}_{\text{V}}} = 1.5{\text{R}}$ and ${{\text{C}}_{\text{P}}} = 2.49{\text{R}}$

Ans .1) The amount of heat required for constant - volume process is: - ${Q_V} = n{C_V}\Delta T$

Here, ${\text{n}} = 2$ moles, ${{\text{C}}_{\text{V}}} = 1.5{\text{R}} = 1.5{\text{X}}8.314\;{\text{J}}/{\text{mol}}{{\text{/}}^0}{\text{C}}$

${{\text{T}}_2} = $ final Temperature

${{\text{T}}_1} = $ Initial Temperature

$\Delta T = {T_2} - {T_1}$

$ = 50 - 20$

$ = {30^0}{\text{C}}$

${{\text{Q}}_{\text{V}}} = 2 \times 1.5 \times 8.314 \times 30$

${{\text{Q}}_{\text{V}}} = 748\;{\text{J}}$

2) The amount of heat required for constant - Pressure process is :-

${Q_p} = n{C_P}\Delta T$

Here, ${\text{n}} = 2$ moles, ${C_P} = 2.49R = 2.49 \times 8.314$

$\Delta T = 30$

${Q_P} = 2 \times 2.49 \times 8.314 \times 30{Q_P} = 1242J$

The change in internal energy is the same in both circumstances since the temperature rise is the same, i.e., 748J. In the constant-pressure process, however, extra heat is delivered, which is employed in the gas expansion.

10. An electric heater supplies heat to a system at a rate of 100W. If system performs work at a rate of 75 Joules per second. At what rate is the internal energy increasing?

Ans: Given Data:

Heat is supplied to the system at a rate of $100\;{\text{W}}$.

$\therefore $ Heat supplied, $Q = 100\;{\text{J}}/{\text{s}}$

The system performs at a rate of $75\;{\text{J}}/{\text{s}}$.

$\therefore $ Work done, $W = 75\;{\text{J}}/{\text{s}}$

From the first law of thermodynamics, we have:

$Q = U + W$

Were,

$U = $ Internal energy

$\therefore U = {\text{Q}} - W$

$ = 100 - 75$

$ = 25\;{\text{J}}/{\text{s}}$

$ = 25\;{\text{W}}$

Therefore, the internal energy of the given electric heater increases at a rate of $25\;{\text{W}}$.

4 Marks Questions

1. A geyser heats water flowing at the rate of 3.0 litres per minute from ${27^0}{\text{C}}$ to ${77^0}{\text{C}}$. If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is $4.0 \times {10^4}\;{\text{J}}/{\text{g}}$ ?

Ans: Given data:

Water is flowing at a rate of 3.0

The geyser heats the water, raising the temperature from 27°C to 77°C

Initial temperature, ${T_1} = {27^0}{\text{C}}$

Final temperature, ${T_2} = {77^0}{\text{C}}$

$\therefore $ Rise in temperature, $\Delta T = {T_2} - {T_1}$

$ = 77 - 27 = {50^0}{\text{C}}$

Heat of combustion $ = 4 \times {10^4}J/g$

Specific heat of water, $c = 4.2\;{\text{J}}\;{{\text{g}}^{ - 1}}^0 {{\text{C}}^{ - 1}}$

Mass of flowing water, $m = 3.0$ litre/min $ = 3000\;{\text{g}}/{\text{min}}$

Total heat used, $\Delta Q = mc\Delta T$

$ = 3000 \times 4.2 \times 50$

$ = 6.3 \times {10^5}\;{\text{J}}/{\text{min}}$

$\therefore $ Rate of consumption $ = \dfrac{{6.3 \times {{10}^5}}}{{4 \times {{10}^4}}} = 15.75\;{\text{g}}/{\text{min}}$

2. What amount of heat must be supplied to $2.0 \times {10^{ - 2}}\;{\text{kg}}$ of nitrogen (at room temperature) to raise its temperature by ${45^0}{\text{C}}$ at constant pressure? (Molecular mass of ${{\mathbf{N}}_2} = {\mathbf{28}};R = 8.3{\mathbf{J}}\;{\mathbf{mo}}{{\mathbf{l}}^{ - 1}}\;{{\text{K}}^{ - 1}}$.)

Ans: Given Data:

Mass of nitrogen, $m = 2.0 \times {10^{ - 2}}\;{\text{kg}} = 20\;{\text{g}}$

Rise in temperature, $\Delta T = {45^0}{\text{C}}$

Molecular mass of ${N_2},M = 28$

Universal gas constant, $R = 8.3\;{\text{J}}\;{\text{mo}}{{\text{l}}^{ - 1}}\;{{\text{K}}^{ - 1}}$

Number of moles, $n = \dfrac{m}{M}$

$ = \dfrac{{2.0 \times {{10}^{ - 2}} \times {{10}^3}}}{{28}} = 0.714$

Molar specific heat at constant pressure for nitrogen, ${C_P} = \dfrac{7}{2}R$

$ = \dfrac{7}{2} \times 8.3$

$ = 29.05{\text{Jmo}}{{\text{l}}^{ - 1}}\;{{\text{K}}^{ - 1}}$

The total amount of heat to be supplied is given by the relation:

$\Delta Q = n{C_P}\Delta T$

$ = 0.714 \times 29.05 \times 45$

$ = 933.38\;{\text{J}}$

Therefore, the amount of heat to be supplied is $933.38\;{\text{J}}$.

3. Explain why.

(a) Two bodies at different temperatures ${T_1}$ and ${T_2}$ if brought in thermal contact do not necessarily settle to the mean temperature $\left( {{T_1} + {T_2}} \right)/2$.

Ans: When two bodies with different temperatures come into thermal contact, heat flows from the higher temperature body to the lower temperature body until equilibrium is reached, i.e., the temperatures of both bodies are equal. When the thermal capacity of both bodies is equal, the equilibrium temperature equals the mean temperature.

(b) The coolant in a chemical or a nuclear plant (i.e., the liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat.

Ans: A chemical or nuclear plant's coolant should have a high specific heat. This is because the coolant's heat-absorbing capability is proportional to its specific heat, and vice versa. As a result, the optimum coolant for a nuclear or chemical plant is a liquid with a high specific heat.

(c) Air pressure in a car tyre increases during driving.

Ans:  When a car is moving, the air temperature within the automobile rises as the air molecules move around. Temperature and pressure are directly related, according to Charles' law. As a result, as the temperature inside a tyre rises, the air pressure inside it rises as well.

(d) The climate of a harbour town is more temperate than that of a town in a desert at the same latitude.

Ans:  A port town has a more temperate environment (i.e., one without extremes of heat or cold) than a town at the same latitude located in a desert. Because the relative humidity in a port town is higher than in a desert town, this is the case.

4. A cylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure. The walls of the cylinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increase if the gas is compressed to half its original volume?

Ans: The cylinder is fully sealed off from the rest of the world. As a result, there is no heat transfer between the system (cylinder) and the environment. Thus, the process is adiabatic.

Initial pressure inside the cylinder $ = {P_1}$

Final pressure inside the cylinder $ = {P_2}$

Initial volume inside the cylinder $ = {V_1}$

Final volume inside the cylinder $ = {V_2}$

Ratio of specific heats, ${\text{Y}} = 1.4$

For an adiabatic process, we have:

${P_1}V_1^y = {P_2}V_2^y$

The final volume is compressed to half of its initial volume.

$\therefore {V_2} = \dfrac{{{V_1}}}{2}$

${P_1}{\left( {{V_1}} \right)^y} = {P_2}{\left( {\dfrac{{{V_1}}}{2}} \right)^y}$

$\dfrac{{{P_2}}}{{{P_1}}} = \dfrac{{{{\left( {{V_1}} \right)}^y}}}{{{{\left( {\dfrac{{{V_1}}}{2}} \right)}^y}}} = {(2)^y} = {(2)^{1.4}} = 2.639$

Hence, the pressure increases by a factor of 2.639.

5. In changing the state of a gas adiabatically from an equilibrium state $A$ to another equilibrium state $B$, an amount of work equal to $22.3\;{\text{J}}$ is done on the system. If the gas is taken from state $A$ to $B$ via a process in which the net heat absorbed by the system is 9.35 Cal, how much is the net work done by the system in the latter case? (Take 1 Cal = 4.19 J)

Ans: The work done ( $W$ ) on the system while the gas changes from state $A$ to state $B$ is $22.3\;{\text{J}}$.

This is an adiabatic process. Hence, change in heat is zero.

$\therefore \Delta Q = 0$

$\Delta W =  - 22.3\;{\text{J}}$ (Since the work is done on the system)

From the first law of thermodynamics, we have:

$\Delta Q = \Delta U + \Delta W$

Were,

$\Delta U = $ Change in the internal energy of the gas

$\therefore \Delta U = \Delta Q - \Delta W =  - ( - 22.3\;{\text{J}})$

$\Delta U =  + 22.3\;{\text{J}}$

When the gas goes from state $A$ to state $B$ via a process, the net heat absorbed by the system is:

$\Delta Q = 9.35{\text{cal}} = 9.35 \times 4.19 = 39.1765\;{\text{J}}$

Heat absorbed, $\Delta Q = \Delta U + \Delta Q$

$\therefore \Delta W = \Delta Q - \Delta U$$ = 39.1765 - 22.3$

$ = 16.8765\;{\text{J}}$Therefore, $16.88\;{\text{J}}$ of work is done by the system.

6. Two cylinders $A$ and $B$ of equal capacity are connected to each other via a stopcock. $A$ contains a gas at standard temperature and pressure. $B$ is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:

(a) What is the final pressure of the gas in ${\mathbf{A}}$ and ${\mathbf{B}}$ ?

Ans: $0.5\;{\text{atm}}$

(b) What is the change in internal energy of the gas?

Ans:  Zero

(c) What is the change in the temperature of the gas?

Ans:  Zero

(d) Do the intermediate states of the system (before settling to the final equilibrium state) lie on its ${\mathbf{P}} - {\mathbf{V}} - {\mathbf{T}}$ surface?

Ans:  No

Explanation:

(a) What is the final pressure of the gas in ${\mathbf{A}}$ and ${\mathbf{B}}$ ?

Ans: As soon as the stopcock between the cylinders is opened, the volume available to the gas is doubled. Because volume and pressure are inversely related, the pressure will drop to one-half of its original value. Because the gas's initial pressure is, each cylinder's pressure will be 0.5 atm.

(b) What is the change in internal energy of the gas?

Ans: The energy released is not evenly distributed across all wavelengths. The energy emitted at its peak, which corresponds to a specific wavelength, and the energy that falls on either side of it. As the temperature of the black body rises. For every given wavelength, the total energy emitted rapidly increases.

(c) What is the change in the temperature of the gas?

Ans: The wavelength at which the most energy is emitted is pushed towards shorter wavelengths.

(d) Do the intermediate states of the system (before settling to the final equilibrium state) lie on its ${\mathbf{P}} - {\mathbf{V}} - {\mathbf{T}}$ surface?

Ans: The given process is a case of free expansion. It is rapid and cannot be controlled. The intermediate states do not satisfy the gas equation and since they are in non-equilibrium states, they do not lie on the $P - V - T$ surface of the system.

5 Marks Questions

1. Derive the equation of state for adiabatic change?

Ans: Let us consider

${\text{P}} = $ pressure, ${\text{V}} = $ volume and ${\text{T}} = $ Temperature of the gas in a cylinder fitted with a perfectly frictionless piston. Suppose a small amount of heat ${\text{dQ}}$ is given to the system. The heat is spent in two ways: -

1) In increasing the temperature of the gas by la small range d ${\text{T}}$, at constant volume

2) In expansion of gas by a small volume ${\text{dv}}$

So, $dQ = {C_V}dT + PdV$

In adiabatic change, no heat is supplied from outside

So, $dQ = 0$

${{\text{C}}_{\text{V}}}{\text{dt}} + {\text{PdV}} = 0 \to (1)$

Acc. to standard gas equation

${\text{PV}} = {\text{RT}}$

Diff both sides

${\text{PdV}} + {\text{VdP}} = {\text{RdR}}$

${\text{RdT}} = {\text{PdV}} + {\text{VdP}}({\text{dR}} = {\text{O}}$ as ${\text{R}}$ is a constant)

${\text{dT}} = \dfrac{{PdV + VdP}}{R}$

Using this in equation i)

${\text{Cv}}\left( {\dfrac{{PdV + VdP}}{R}} \right) + {\text{PdV}} = {\text{O}}$

${{\text{C}}_{\text{V}}}{\text{PdV}} + {{\text{C}}_{\text{V}}}{\text{VdP}} + {\text{RPdV}} = {\text{O}}$

$\left. {\left( {{C_V} + R} \right)PdV + {C_V}VdP = 0 \to 2} \right)$

As, ${{\text{C}}_{\text{P}}} - {{\text{C}}_{\text{V}}} = {\text{R}}$or ${C_p} = R + {C_V}$So equation 2) becomes${{\text{C}}_{\text{P}}}{\text{PdV}} + {{\text{C}}_{\text{V}}}{\text{VdP}} = {\text{O}}$

Dividing above equation by ${{\text{C}}_{\text{V}}}{{\text{P}}_{\text{V}}}$

$\dfrac{{{C_P}PdV}}{{{C_V}PV}} + \dfrac{{{C_V}VdP}}{{{C_V}PV}} = O\left( {\because \dfrac{{{C_P}}}{{{C_V}}} = 4} \right)$

$\gamma \dfrac{{dV}}{V} + \dfrac{{dP}}{P} = O$

Integrating both sides

$\gamma \int {\dfrac{{{\text{dV}}}}{{\text{V}}}}  + \int {\dfrac{{{\text{dP}}}}{{\text{P}}}}  = \int {\text{O}} $

$\gamma $ Loge ${\text{V}} + $ Loge ${\text{P}} = $ constant

Loge ${V^\gamma } + $ Loge ${\text{P}} = $ constant $\left( {\because a\log {\text{b}} = \log {{({\text{b}})}^{\text{a}}}} \right)$

Loge ${\text{P}}{V^y} = $ constant $(\because \log a + \log b = \log ab)$

${\text{P}}{{\text{V}}^\gamma } = $ antilog (constant)

$P{V^\gamma } = K$

${\text{K}} = $ another constant

2. Derive an expression for the work done during isothermal expansion?

Ans: Assume that one gramme mole of ideal gas has the following properties: pressure, volume, and temperature. Allow the gas to expand to a volume of while the pressure drops to and the temperature remains constant.

If ${\text{A}} = $ Area of cross - section of piston

Force = Pressure $ \times $ Area

${\text{F}} = {\text{P}} \times {\text{A}}$

If we assume that piston moves a displacement d ${\text{x}}$,

the work done $: \to {\text{dw}} = {\text{Fdx}}$

${\text{dw}} = {\text{P}} \times {\text{A}} \times {\text{dx}}$${\text{dw}} = {\text{p}} \times {\text{dv}}$ 

Total work done in increasing the volume from ${{\text{V}}_1}$ to ${{\text{V}}_2}$.

So ${\text{W}} = 2.3026{\text{RT}}\log 10\left( {\dfrac{{{P_1}}}{{{P_2}}}} \right)$

3. Briefly describe a Carnot cycle and derive an expression for the efficiency of Carnot cycle?

Ans:
The following are the components of a Carnot cycle heat engine:

1) Source of heat: It is kept at a higher temperature

2) Heat sink - It is kept at a lower temperature.

3) Working material: The working substance is a perfect ideal gas.

Theorem

The Carnot cycle has four stages:

1) thermal expansion.

2)Adiabatic expansion is a type of adiabatic expansion.

3) thermal compression.

4) Compression adiabatic.

4. Discuss briefly energy distribution of a black body radiation. Hence deduce Wien’s displacement law?

Ans: For a black body, the monochromatic emittance $(E\pi )$ of the black body and the

wavelength $(\lambda )$ of the radiation emitted.

So, at a given temperature of black body:

a) The energy released is not evenly distributed across all wavelengths.

b) The energy emitted at its peak, which corresponds to a specific wavelength, and the energy that falls on either side of it.

As the temperature of the black body rises.

a) For every given wavelength, the total energy emitted rapidly increases.

b) The wavelength at which the most energy is emitted is pushed towards shorter wavelengths.

$ \Rightarrow $ This is the Wein’s displacement law.

Important Related Links for CBSE Class 11