Important Questions for CBSE Class 11 Physics Chapter 6 - Systems of Particles and Rotational Motion

Very short answer questions (1 Mark)

1. A wheel $ 0.5m$ in radius is moving with a speed of $ 12m/s$ . Find its angular speed.

Ans: Angular speed can be given as $ v=r\omega $ 

$ \Rightarrow \omega =\dfrac{v}{r}=\dfrac{12}{0.5}$ 

$ \Rightarrow \omega =24rad/s$ 

2. State the condition for translational equilibrium of a body.

Ans: For a body to be in a translational equilibrium, the vector sum of all the forces acting on the body must be equal to zero.

3. How is angular momentum related to linear momentum?

Ans: Angular momentum can be related as $ \vec{L}=\vec{r}\times \vec{p}$ 

Or $ L=rp\sin \theta $ 

Where $ \theta $ is the angle between $ \vec{r}$ and $ \vec{p}$ .

4. What is the position of the centre of mass of a uniform triangular lamina?

Ans: The centre of mass of a uniform triangular lamina is at the centroid of the triangular lamina.

5. What is the moment of inertia of a sphere of mass $ 20kg$ and radius $ \dfrac{1}{4}m$ about its diameter?

Ans: $ I=\dfrac{2}{5}M{{R}^{2}}$ 

$ I=\dfrac{2}{5}\times 20\times {{\left( \dfrac{1}{4} \right)}^{2}}$ 

$ I=0.5kg{{m}^{2}}$ 

6. What are the factors on which moment of inertia of a body depends?

Ans: Moment of inertia of a body depends on: 

• Mass of the body

• Shape and size of the body

• Position of the axis of rotation

7. Two particles in an isolated system undergo head on collision. What is the acceleration of the centre of mass of the system?

Ans: Acceleration of the centre of mass of the system is zero.

8. Which component of a force does not contribute towards torque?

Ans: The component of a force that does not contribute towards torque is the radial component.

9. What is the position of centre of mass of a rectangular lamina?

Ans: The point of intersection of diagonal is the position of the centre of mass of a rectangular lamina.

10. Give the location of the centre of mass of a 

1. sphere, 

2. cylinder, 

3. ring, and 

4. cube, each of uniform mass density.

Does the centre of mass of a body necessarily lie inside the body?

Ans: The centre of mass (C.M.) can be defined as a point where the mass of a body is supposed to be concentrated.

For the above listed geometric shapes having a uniform mass density, the centre of mass lies at their respective geometric centres.

The centre of mass of a specific body need not necessarily lie inside of the body. For example, the centre of mass of bodies such as a ring, a hollow sphere, etc., lies outside the respective body.

11. A child sits stationary at one end of a long trolley moving uniformly with a speed $ v$ on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?

Ans: There will not be any change in the speed of the centre of mass of the given system. The child is running arbitrarily on a trolley that is moving forward with velocity $ v$ . However, the running of the child will have no effect on the velocity of the centre of mass of the trolley. This happens because of the force due to the motion of child is purely internal. 

Internal forces in a body produce no effect on the motion of the bodies on which they are acting. Because there is no external force involved in the (child + trolley) system, the child’s motion will not produce any change in the speed of the centre of mass of the trolley.

12. To maintain a rotor at a uniform angular speed of $ 200rad\,\,{{s}^{-1}}$ an engine needs to transmit a torque of $ 180Nm$ . What is the power required by the engine? (Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is $ 100%$ efficient.

Ans: Angular speed of the rotor is given as, $ 200rad/s$ .

Torque required by the rotor of the engine is given as $ 180Nm$ .

The power of the rotor $ \left( P \right)$ can be expressed in the relation of torque and angular speed by the formula $ P=\tau \omega $ 

$ \Rightarrow P=180\times 200=30\times {{10}^{3}}$ 

$ \Rightarrow P=36kW$ 

Therefore, the power required by the engine is $ 36kW$ .

Short Answer Questions (2 Marks)

1. A planet revolves around on massive star in a highly elliptical orbit is its angular momentum constant over the entire orbit. Give reason?

Ans: When a planet revolves around the star, it takes place under the effect of gravitational force. The force is radial and does not contribute towards torque. Hence, in the absence of an external torque angular momentum of the planet remains constant.

2. Obtain the equation $ \omega ={{\omega }_{0}}+\alpha t$ .

Ans: We know the relation,

$ \alpha =\dfrac{d\omega }{dt}$ 

$ d\omega =\alpha dt$ 

Integrating within the limits

$ \int_{{{\omega }_{0}}}^{\omega }{d\omega =\int_{0}^{t}{\alpha dt}}$ 

$ \Rightarrow \omega -{{\omega }_{0}}=\alpha t$ 

$ \Rightarrow \omega ={{\omega }_{0}}+\alpha t$ 

Hence, proved.

3. What is the torque of the force $ \vec{F}=2\hat{i}-5\hat{j}+4\hat{k}$ acting at the point $ \vec{r}=\left( 3\hat{i}+3\hat{j}+3\hat{k} \right)m$ about the origin?

Ans: Torque is given by

$ \vec{\tau }=\vec{r}\times \vec{F}$ 

$ \Rightarrow \vec{\tau } = \left[\begin{array}{ccc} {\hat{i}} & {\hat{j}} & {\hat{k}} \\ 2 & -3 & 4 \\ 3 & 2 & 3 \end{array}\right]$ 

$ \Rightarrow \vec{\tau }=\left( 17\hat{i}-6\hat{j}-13\hat{k} \right)Nm$ 

4. What is the value of linear velocity if $ \vec{\omega }=\left( 3\hat{i}-4\hat{j}+\hat{k} \right)$ and $ \vec{r}=\left( 5\hat{i}-6\hat{j}+6\hat{k} \right)$ .

Ans: Linear velocity is given by

$ \vec{\upsilon }=\vec{\omega }\times \vec{r}$ 

$ \Rightarrow \vec{\upsilon }=\left( 3\hat{i}-4\hat{j}+\hat{k} \right)\times \left( 5\hat{i}-6\hat{j}+6\hat{k} \right)$ 

$ \Rightarrow \vec{\upsilon }=-18\hat{i}-13\hat{j}+2\hat{k}$ 

5. Establish the third equation of rotational motion $ {{\omega }^{2}}-{{\omega }_{0}}^{2}=2\alpha \theta $ .

Ans: We have the relation, $ \alpha =\dfrac{d\omega }{dt}$ 

Multiply and divide by $ d\theta $ 

$ \alpha =\dfrac{d\omega }{dt}\times \dfrac{d\theta }{d\theta }$ 

$ \Rightarrow \alpha =\dfrac{d\omega }{d\theta }\times \dfrac{d\theta }{dt}$ 

$ \Rightarrow \alpha d\theta =\omega d\omega $ 

Integrating we get

$ \int_{0}^{\theta }{\alpha d\theta }=\int_{{{\omega }_{0}}}^{\omega }{\omega d\omega }$ 

$ \Rightarrow \alpha \left[ \theta \right]_{0}^{\theta }=\left[ \dfrac{{{\omega }^{2}}}{2} \right]_{{{\omega }_{0}}}^{\omega }$ 

$ \Rightarrow \alpha \theta =\dfrac{{{\omega }^{2}}}{2}-\dfrac{{{\omega }_{0}}^{2}}{2}$ 

$ \Rightarrow {{\omega }^{2}}-{{\omega }_{0}}^{2}=2\alpha \theta $ 

Hence, proved.

6. Find the expression for radius of gyration of a solid sphere about one of its diameters.

Ans: Moment of inertia of a solid sphere about its diameter can be given as,

$ =\dfrac{2}{5}M{{R}^{2}}$ 

$ K=$ Radius of Gyration

$ I={M}{{K}^{2}}=\dfrac{2}{5}{M}{{R}^{2}}$ 

$ \Rightarrow {{K}^{2}}=\dfrac{2}{5}{{R}^{2}}$ 

$ \Rightarrow K=\sqrt{\dfrac{2}{5}}R$ 

7. Prove that the centre of mass of two particles divides the line joining the particles in the inverse ratio of their masses?

Ans: We can express the relation as $ {{\vec{r}}_{cm}}=\dfrac{{{m}_{1}}{{{\vec{r}}}_{1}}+{{m}_{2}}{{{\vec{r}}}_{2}}}{{{m}_{1}}+{{m}_{2}}}$ 

If centre of mass is at the origin,

$ \Rightarrow {{\vec{r}}_{cm}}=0$ 

$ \Rightarrow {{m}_{1}}{{\vec{r}}_{1}}+{{m}_{2}}{{\vec{r}}_{2}}=0$ 

$ {{m}_{1}}{{\vec{r}}_{1}}=-{{m}_{2}}{{\vec{r}}_{2}}$ 

In terms of magnitude, it can be expressed as,

$ {{m}_{1}}\left| {{{\vec{r}}}_{1}} \right|={{m}_{2}}\left| {{{\vec{r}}}_{2}} \right|$ 

$ \Rightarrow \dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{{{r}_{2}}}{{{r}_{1}}}$ 

8. Show that cross product of two parallel vectors is zero.

Ans: $ \vec{A}\times \vec{B}=AB\sin \theta \hat{x}$ 

 If $ \vec{A}$ and $ \vec{B}$ are parallel to each other,

Then, $ \theta ={{0}^{\circ }}$ 

$ \Rightarrow \vec{A}\times \vec{B}=0$ 

9. Prove the relation $ \overrightarrow{\tau }=\dfrac{d\overrightarrow{L}}{dt}$ .

Ans: We are aware of the relation, $ \overrightarrow{L}=I\overrightarrow{\omega }$ 

Differentiating on both sides with respect to time

$ \dfrac{d\vec{L}}{dt}=\dfrac{d}{dt}\left( I\vec{\omega } \right)=I\dfrac{d\vec{\omega }}{dt}=I\vec{\alpha }$ …… (1)

Where, $ \vec{L}=$ Angular Momentum

$ \vec{\tau }=$ Torque

And $ \dfrac{d\vec{\omega }}{dt}=\vec{\alpha }$ 

$ \Rightarrow \vec{\tau }=I\vec{\alpha }$ …… (2)

From (1) and (2)

$ \vec{\tau }=\dfrac{d\vec{L}}{dt}$ 

Hence, proved.

10. Show that for an isolated system the centre of mass moves with uniform velocity along a straight line path.

Ans: For the given conditions let $ \vec{M}$ be the total mass concentrated at centre of mass whose position vector is $ \overrightarrow{r}$ .

$ \vec{F}=\dfrac{M{{d}^{2}}\vec{r}}{d{{t}^{2}}}$ 

$ \Rightarrow \vec{F}=\dfrac{Md}{dt}\left( \dfrac{d\vec{r}}{dt} \right)=\dfrac{Md}{dt}\left( {{{\vec{V}}}_{cm}} \right)$ 

For an isolated system it can be given as, $ \overrightarrow{F}=0$ 

$ \Rightarrow \dfrac{Md}{dt}\left( {{{\vec{V}}}_{cm}} \right)=0$ 

Or $ \dfrac{d}{dt}\left( {{{\vec{V}}}_{cm}} \right)=0$ since $ M\ne 0$ 

$ \Rightarrow \left( {{{\vec{V}}}_{cm}} \right)=constant$ 

11. The angle $ \theta $ covered by a body in rotational motion is given by the equation $ \theta =6t+5{{t}^{2}}+2{{t}^{3}}$ . Determine the value of instantaneous angular velocity and angular acceleration.

at time $ t=2s$ .

Ans: In the question it is given that $ \theta =6t+5{{t}^{2}}+2{{t}^{3}}$ .

Now, Angular velocity $ \omega =\dfrac{d\theta }{dt}=6+10t+6{{t}^{2}}$ 

At $ t=2s$ 

$ \omega =6+10\left( 2 \right)+6{{\left( 2 \right)}^{2}}$ 

$ \Rightarrow \omega =50rad/\sec $ 

Again, angular acceleration can be given as,

$ \alpha =\dfrac{d\omega }{dt}=\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}=10+12t$ 

At $ t=2s$ 

$ \alpha =10+12\left( 2 \right)$ 

$ \alpha =34rad/{{s}^{2}}$ 

12. A solid cylinder of mass $ 20kg$ rotates about its axis with angular speed $ 100rad/\sec $ . The radius of the cylinder is $ 0.25m$ . What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?

Ans: Mass of the cylinder is given as, $ m=20kg$ 

Angular speed is given as, $ \omega =100rad/s$ 

Radius of the cylinder, $ r=0.25m$ 

The moment of inertia of the solid cylinder can be given as:

$ I=\dfrac{m{{r}^{2}}}{2}$ 

Now,

$ \Rightarrow I=\dfrac{1}{2}\times 20\times {{\left( 0.25 \right)}^{2}}$ 

$ \Rightarrow I=0.625kg{{m}^{2}}$ 

Kinetic energy can be given as: $ K.E.=\dfrac{1}{2}I{{\omega }^{2}}$ 

$ \Rightarrow K.E.=\dfrac{1}{2}\times 6.25\times {{\left( 100 \right)}^{2}}=3125J$ 

Angular momentum can be given as, 

$ L=I\omega $ 

$ \Rightarrow L=6.25\times 100$ 

$ \Rightarrow L=62.5Js$ 

13. A rope of negligible mass is wound round a hollow cylinder of mass $ 3kg$ and radius $ 40cm$ . What is the angular acceleration of the cylinder if the rope is pulled with a force of $ 30N$ ? What is the linear acceleration of the rope? Assume that there is no slipping.

Ans: Given that,

Mass of the hollow cylinder is given as, $ m=3kg$ 

Radius of the hollow cylinder is given as, $ r=40cm=0.4m$ 

Applied force on the given rope is given as, $ F=30N$ 

The moment of inertia of the hollow cylinder about its geometric axis can be given as:

$ I=m{{r}^{2}}$ 

$ \Rightarrow I=3\times {{\left( 0.4 \right)}^{2}}$ 

$ \Rightarrow I=0.48kg{{m}^{2}}$ 

Torque acting on the rope,

$ \tau =F\times r$ 

$ \Rightarrow \tau =30\times 0.4$ 

$ \Rightarrow \tau =12Nm$ 

For angular acceleration $ \alpha $ , torque can also be given by the expression:

$ \tau =I\alpha $ 

$ \Rightarrow \alpha =\dfrac{\tau }{I}=\dfrac{12}{0.48}$ 

$ \Rightarrow \alpha =25rad\,{{s}^{-2}}$ 

Linear acceleration of the rope can be stated as $ =ra=0.4\times 25=10m{{s}^{-2}}$ .

14. A bullet of mass $ 10g$ and speed $ 500m/s$ is fired into a door and gets embedded exactly at the centre of the door. The door is $ 1.0m$ wide and weighs $ 12kg$ . It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it. (Hint: The moment of inertia of the door about the vertical axis at one end is $ \dfrac{M{{L}^{2}}}{3}$ .) 

Ans: Given that,

Mass of the bullet is given as, $ m=10g=10\times {{10}^{-3}}kg$ 

Velocity of the bullet is given as, $ v=500m/s$ 

Width of the door, $ L=1.0m$ 

Radius of the door, $ r=\dfrac{1}{2}m$ 

Mass of the door is given, $ M=12kg$ 

Angular momentum transmitted by the bullet on the door:

$ \alpha =mvr$ 

$ \Rightarrow \alpha =\left( 100\times {{10}^{-3}} \right)\times \left( 500 \right)\times \dfrac{1}{2}=2.5kg{{m}^{2}}{{s}^{-1}}$ 

Moment of inertia of the door can be given as:

$ I=\dfrac{M{{L}^{2}}}{3}$ 

$ \Rightarrow I=\dfrac{1}{3}\times 12\times {{\left( 1 \right)}^{2}}=4kg{{m}^{2}}$ 

But we have the relation,

$ \alpha =I\omega $ 

$ \Rightarrow \omega =\dfrac{\alpha }{I}=\dfrac{2.5}{4}=0.625rad{{s}^{-1}}$ , which is the required angular speed.

15. Explain why friction is necessary to make the disc in Fig. 7.41 roll in the direction indicated.

(a). Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins. 

Ans: To roll the given disc, some torque is necessary. As per the definition of torque, the rotating force must be tangential to the disc. Since the frictional force at point $ B$ is along the tangential force at point $ A$ , a frictional force is necessary for making the disc roll.

Force of friction will act in the opposite direction to the direction of velocity at point $ B$ . The direction of linear velocity at point $ B$ can be pointed tangentially leftward. Therefore, frictional force will act tangentially rightward. The frictional torque before the start of perfect rolling is perpendicular to the plane of the disc in the outward direction.

(b). What is the force of friction after perfect rolling begins?

Ans: Since frictional force will act opposite to the direction of velocity at point $ B$ , perfect rolling will start when the velocity at that point becomes equal to zero. This will make the frictional force that acts on the disc as zero.

Long Answer Questions (3 Marks)

1. The moment of inertia of a solid sphere about a tangent is $ \dfrac{7}{5}M{{R}^{2}}$ . Find the moment of inertia about a diameter.

Ans: From the diagram we can infer that a tangent $ KCL$ is drawn at point $ C$ of a solid sphere of mass $ M$ and radius $ R$ . Now, draw a diameter $ AOB\parallel KCL$ .

Then according to Theorem of parallel axis, $ {{I}_{1}}=I+M{{\left( OC \right)}^{2}}$ 

M.I about the tangent can be given as $ {{I}_{1}}=\dfrac{7}{5}M{{R}^{2}}$ 

$ I={{I}_{1}}-M{{\left( OC \right)}^{2}}$ 

$ \Rightarrow I=\dfrac{7}{5}M{{R}^{2}}-M{{R}^{2}}$ 

$ \Rightarrow I=\dfrac{2}{5}M{{R}^{2}}$ , which is the moment of inertia about a diameter.

2. Four particles of mass $ 1kg$ , $ 2kg$ , $ 3kg$ and $ 4kg$ are placed at the four vertices $ A$ , $ B$ , $ C$ and $ D$ of square of side $ 1m$ . Find the position of centre of mass of the particle.

Ans: From the given data we can infer,

$ {{m}_{1}}=1kg$ at $ \left( {{x}_{1}},{{y}_{1}} \right)=\left( 0,0 \right)$ 

$ {{m}_{2}}=2kg$ at $ \left( {{x}_{2}},{{y}_{2}} \right)=\left( 1,0 \right)$ 

$ {{m}_{3}}=3kg$ at $ \left( {{x}_{3}},{{y}_{3}} \right)=\left( 1,1 \right)$ 

$ {{m}_{4}}=4kg$ at $ \left( {{x}_{4}},{{y}_{4}} \right)=\left( 0,1 \right)$ 

Now, 

$ {{X}_{cm}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}+{{m}_{4}}{{x}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$ 

$ \Rightarrow {{X}_{cm}}=0.5m$ 

$ {{Y}_{cm}}=\dfrac{{{m}_{1}}{{y}_{1}}+{{m}_{2}}{{y}_{2}}+{{m}_{3}}{{y}_{3}}+{{m}_{4}}{{y}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$ 

$ \Rightarrow {{Y}_{cm}}=0.7m$ 

Therefore, the centre of mass is located at $ \left( 0.5m,0.7m \right)$ .

3. A circular ring of diameter $ 40cm$ and mass $ 1kg$ is rotating about an axis normal to its plane and passing through the centre with a frequency of $ 10$ rotations per second. Calculate the angular momentum about its axis of rotation.

Ans: From the question we can write,

$ R=\dfrac{40}{2}cm=20cm=0.2m$ 

$ M=1kg$ 

$ v=10 rotations/\sec $ 

Now, Moment of inertia can be calculated as,

$ M.I.=M{{R}^{2}}=1\times {{\left( 0.2 \right)}^{2}}=0.04kg{{m}^{2}}$ 

$ \omega =2\pi v=2\pi \times 10=20\pi rad/s$ 

Angular momentum can be calculated as,

$ \Rightarrow L=0.04\times 20\pi $ 

$ \Rightarrow L=2.51kg{{m}^{2}}/s$ 

4. 

(a). Which physical quantities are represented by the

(i) Rate of change of angular momentum?

Ans: Torque i.e., $ \tau =\dfrac{d\vec{L}}{dt}$ 

(ii) Product of $ I$ and $ \vec{\omega }$ ?

Ans: Angular momentum i.e., $ L=I\omega $ 

(b). Show that angular momentum of a satellite of mass $ {{M}_{s}}$ revolving around the earth having mass $ {{M}_{e}}$ in an orbit of radius $ r$ is equal to

Ans: Given that

Mass of satellite is given as $ ={{M}_{s}}$ 

Mass of earth is given as $ ={{M}_{e}}$ 

Radius of satellite is given as $ =r$ 

Required centripetal force can be given as $ =\dfrac{{{M}_{s}}{{v}^{2}}}{r}$ …… (1)

Where $ v$ is the orbital velocity with which the satellite revolves around the earth.

Now, Gravitational force between the satellite and the earth can be given as:

$ =\dfrac{G{{M}_{e}}{{M}_{s}}}{{{r}^{2}}}$ …… (2)

Equating equations (1) and (2)

$ \dfrac{{{M}_{s}}{{v}^{2}}}{r}=\dfrac{G{{M}_{e}}{{M}_{s}}}{{{r}^{2}}}$ 

$ \Rightarrow v=\sqrt{\dfrac{G{{M}_{e}}}{r}}$ 

Now angular momentum of the satellite can be given as,

$ L={{M}_{s}}vr$ 

$ \Rightarrow L={{M}_{s}}\times \sqrt{\dfrac{G{{M}_{e}}}{r}}\times r$ 

$ \Rightarrow L=\sqrt{G{{M}_{e}}{{M}_{s}}^{2}r}$ 

Hence, proved

5. In the $ HCl$ molecule, the separation between the nuclei of the two atoms is about $1.27 {\overset{o}{A}}$ $20kg$ . Find the approximate location of the CM of the molecule, given that a chlorine atom is about $ 35.5$ times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.

Ans: The provided situation can be expressed as:

Distance between $ H$ and $ Cl $ atoms $ =1.27 \overset{o}{A}$ 

Mass of $ H$ atom $ =m$ 

Mass of $ Cl$ atom $ =35.5m$ 

Let the centre of mass of the given system be at a distance $ x$ from the $ Cl$ atom.

Distance between the centre of mass and the $ H$ atom $ =\left( 1.27-x \right)$ 

Let us suppose that the centre of mass of the given molecule lies at the origin. Therefore, it can be written as:

$ \dfrac{m\left( 1.27-x \right)+35.5mx}{m+35.5m}=0$ 

$ \Rightarrow m\left( 1.27-x \right)+35.5mx=0$ 

$ \Rightarrow 1.27-x=-35.5x$ 

$ \Rightarrow x=\dfrac{-1.27}{\left( 35.5-1 \right)} = -0.037 {\overset{o}{A}}$ 

Here, the negative sign gives an indication that the centre of mass lies at the left side of the molecule.

Therefore, the centre of mass of the $ HCl$ molecule lies $ 0.037 \overset{o}{A}$ from the $ Cl$ atom.

6. Show that the area of the triangle contained between the vectors $ a$ and $ b$ is one half of the magnitude of $ a\times b$ .

Ans: Let us consider two vectors $ \overrightarrow{OK}=\left| \overrightarrow{a} \right|$ and $ \overrightarrow{OM}=\left| \overrightarrow{b} \right|$ , which are inclined at an angle $ \theta $ , as shown in the following figure.

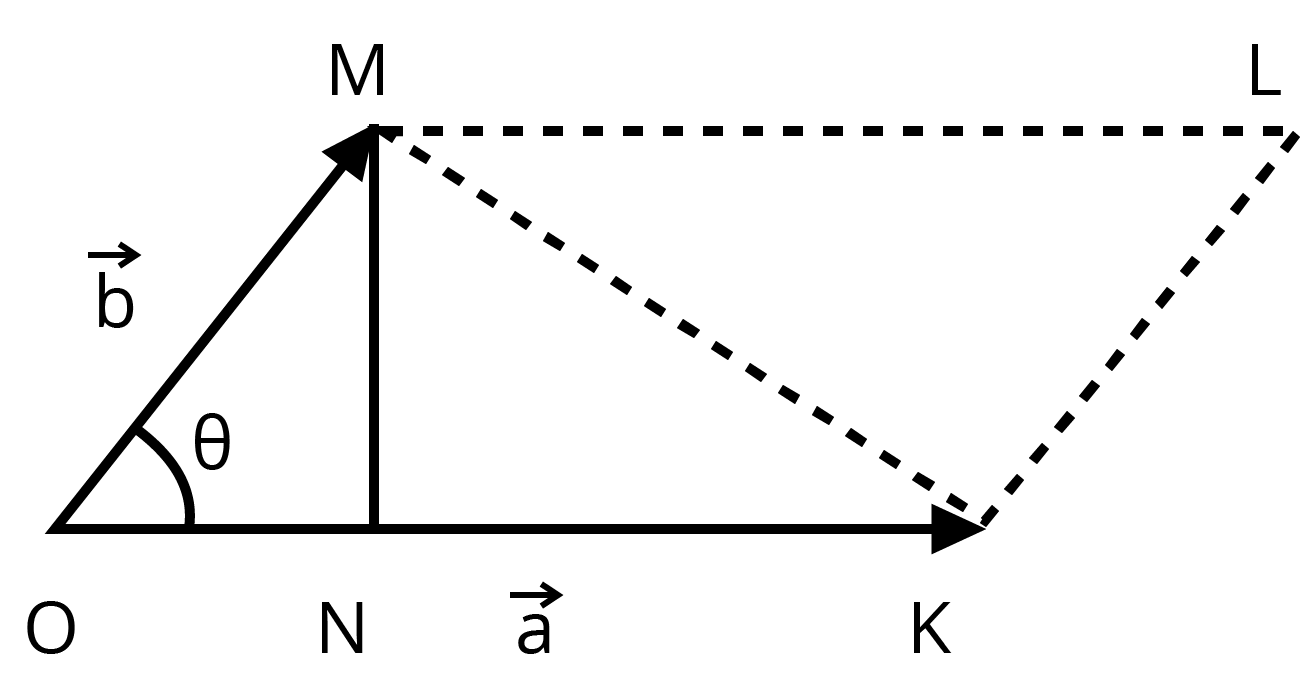
In $ \Delta OMN$ , we can express the relation:

$ \sin \theta =\dfrac{MN}{OM}=\dfrac{MN}{\left| \overrightarrow{b} \right|}$ 

$ \Rightarrow MN=\left| \overrightarrow{b} \right|\sin \theta $ 

Now, 

$ \left| \overrightarrow{a}\times \overrightarrow{b} \right|=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\sin \theta $ 

$ \Rightarrow \left| \overrightarrow{a}\times \overrightarrow{b} \right|=OK\cdot MN\times \dfrac{2}{2}$ 

$ \Rightarrow \left| \overrightarrow{a}\times \overrightarrow{b} \right|=2\times Area\,of\,\Delta OMK$ 

$ \Rightarrow Area\,of\,\Delta OMK=\dfrac{1}{2}\left| \overrightarrow{a}\times \overrightarrow{b} \right|$ 

7. A meter stick is balanced on a knife edge at its centre. When two coins, each of mass $ 5g$ are put one on top of the other at the $ 12cm$ mark, the stick is found to be balanced at $ 45cm$ . What is the mass of the meter stick?

Ans: Let us assume that $ W$ and $ {W}'$ be the respective weights of the meter stick and the coin.

The mass of the meter stick is supposed to be concentrated at its mid-point, i.e., at the $ 50cm$ mark.

Mass of the meter stick is $ {m}'$ 

Mass of each coin is $ m=5g$ 

When the coins are placed $ 12cm$ away from the end $ P$ , the centre of mass gets shifted by $ 5cm$ from point $ R$ toward the end $ P$ . The centre of mass is located at a distance of $ 45cm$ from point $ P$ .

The net torque will be thus conserved for rotational equilibrium about point $ R$ .

This can be expressed by the equation,

$ 10\times g\left( 45-12 \right)-{m}'g\left( 50-45 \right)=0$ 

$ \Rightarrow {m}'=\dfrac{10\times 33}{5}=66g$ 

Therefore, the mass of the meter stick is $ 66g$ .

Long Answer Questions (4 Marks)

1. Show that $ a\cdot \left( b\times c \right)$ is equal in magnitude to the volume of the parallelepiped formed on the three vectors, $ a$ , $ b$ and $ c$ .

Ans: A parallelepiped with origin $ O$ and sides $ a$ , $ b$ , and $ c$ is depicted in the following figure.

Volume of the given parallelepiped $ =abc$ 

And 

$ \overrightarrow{OA}=\vec{a}$ 

$ \overrightarrow{OB}=\vec{b}$ 

$ \overrightarrow{OC}=\vec{c}$ 

Let us suppose that $ n$ be a unit vector perpendicular to both $ b$ and $ c$ . Therefore,

$ n$ and $ a$ have the same direction.

$ \vec{b}\times \vec{c}=bc\sin \theta n$ 

$ \Rightarrow \vec{b}\times \vec{c}=bc\sin {{90}^{\circ }}n$ 

$ \Rightarrow \vec{b}\times \vec{c}=bcn$ 

Now,

$ \vec{a}\left( \vec{b}\times \vec{c} \right)=a\cdot \left( bcn \right)$ 

$ \Rightarrow \vec{a}\left( \vec{b}\times \vec{c} \right)=abc\cos \theta \hat{n}$ 

$ \Rightarrow \vec{a}\left( \vec{b}\times \vec{c} \right)=abc\cos {{0}^{\circ }}\hat{n}$ 

$ \Rightarrow \vec{a}\left( \vec{b}\times \vec{c} \right)=abc\cos {{0}^{\circ }}$ 

$ \Rightarrow \vec{a}\left( \vec{b}\times \vec{c} \right)=abc$ 

$ \Rightarrow \vec{a}\left( \vec{b}\times \vec{c} \right)=abc=Volume\,of\,the\,parallelepiped$ 

2. A hoop of radius $ 2m$ weighs $ 100kg$ . It rolls along a horizontal floor so that its centre of mass has a speed of $ 20cm/s$ . How much work has to be done to stop it?

Ans: Given that,

Radius of the hoop is given as, $ r=2m$ 

Mass of the hoop is, $ m=100kg$ 

Velocity of the hoop is,

$ v=20cm/s=0.2m/s$ 

Total energy of the hoop $ =$ Translational KE $ +$ Rotational KE

$ {{E}_{r}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}}$ 

Moment of inertia of the hoop about its centre can be given as $ I=m{{r}^{2}}$ 

$ {{E}_{r}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}\left( m{{r}^{2}} \right){{\omega }^{2}}$ 

But we have the formula, $ v=r\omega $ 

$ \Rightarrow {{E}_{1}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}m{{r}^{2}}{{\omega }^{2}}$ 

$ \Rightarrow {{E}_{1}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}m{{v}^{2}}=m{{v}^{2}}$ 

The work needed to be done for halting the hoop is same to the total energy of the hoop.

Hence, required work to be done can be given as,

$ W=m{{v}^{2}}=100\times {{\left( 0.2 \right)}^{2}}=4J$ 

3. The oxygen molecule has a mass of $ 5.30\times {{10}^{26}}kg$ and a moment of inertia of $ 1.94\times {{10}^{-46}}kg{{m}^{2}}$ about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is $ 500m/s$ and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.

Ans: Given that,

Mass of an oxygen molecule is given as, $ m=5.30\times {{10}^{26}}kg$ 

Moment of inertia of oxygen molecule is given as, $ I=1.94\times {{10}^{-46}}kg{{m}^{2}}$ 

Velocity of the oxygen molecule is given as, $ v=500m/s$ 

Let the separation between the two atoms of the oxygen molecule be $ 2r$ 

Mass of each oxygen atom in the oxygen molecule $ =\dfrac{m}{2}$ 

Therefore, moment of inertia $ I$ , can be calculated as:

$ \left( \dfrac{m}{2} \right){{r}^{2}}+\left( \dfrac{m}{2} \right){{r}^{2}}=m{{r}^{2}}$ 

$ r=\sqrt{\dfrac{l}{m}}$ 

$ \Rightarrow \sqrt{\dfrac{1.94\times {{10}^{-46}}}{5.36\times {{10}^{26}}}}=0.60\times {{10}^{-10}}m$ 

It is provided that:

$ K{{E}_{rot}}=\dfrac{2}{3}K{{E}_{trans}}$ 

$ \Rightarrow \dfrac{1}{2}I{{\omega }^{2}}=\dfrac{2}{3}\times \dfrac{1}{2}m{{v}^{2}}$ 

$ \Rightarrow m{{r}^{2}}{{\omega }^{2}}=\dfrac{2}{3}m{{v}^{2}}$ 

$ \Rightarrow \omega =\sqrt{\dfrac{2}{3}}\times \dfrac{v}{r}$ 

$ \Rightarrow \omega =\sqrt{\dfrac{2}{3}}\times \dfrac{500}{0.6\times {{10}^{-10}}}$ 

$ \Rightarrow \omega =6.80\times {{10}^{12}}rad/s$ , which is the required average angular velocity of the molecule.

4. A man stands on a rotating platform, with his arms stretched horizontally holding a $ 5kg$ weight in each hand. The angular speed of the platform is $ 30$ revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from $ 90cm$ to $ 20cm$ . The moment of inertia of the man together with the platform may be taken to be constant and equal to $ 7.6kg{{m}^{2}}$ .

(a). What is his new angular speed? (Neglect friction.)

Ans: Moment of inertia of the man-platform system is given as, 

$ 7.6kg{{m}^{2}}$ 

Moment of inertia when the man stretches his hands to a distance of 90 cm:

$ M{{I}_{Hands\,Stretched}}=2\times m{{r}^{2}}$ 

$ \Rightarrow {M{I}_{Hands\,Stretched}} = 2\times 5\times {{\left( 0.9 \right)}^{2}}$ 

$ \Rightarrow {M{I}_{Hands\,Stretched}} = 8.1kg{{m}^{2}}$ 

Initial moment of inertia of the system can be given as,

$ {{I}_{i}} = 7.6+8.1=15.7kg{{m}^{2}}$ 

Angular speed can be expressed as,

$ {{\omega }_{1}}=300rev/ \min $ 

Angular momentum can be given as,

$ {{L}_{i}} = {{I}_{i}}{{\omega }_{i}}=15.7\times 30$ …… (1)

Moment of inertia when the man folds his hands to a distance of 20 cm becomes:

$ M{{I}_{Hands\,at\,20cm}}=2m{{r}^{2}}$ 

$ \Rightarrow {M{I}_{Hands\,at\,20cm}}=2\times 5{{\left( 0.2 \right)}^{2}}=0.4kg{{m}^{2}}$ 

Final moment of inertia is given as,

$ {{I}_{f}} = 7.6 + 0.4 = 8kg{{m}^{2}}$ 

Final angular speed can be given as, $ {{\omega }_{f}}$ 

Final angular momentum can be expressed as,

$ {{L}_{f}} = {{I}_{f}}{{\omega }_{f}} = 0.79\omega $ …… (2)

From the conservation of angular momentum, we can write:

$ {{I}_{i}}{{\omega }_{i}} = {{I}_{f}}{{\omega }_{f}}$ 

$ {{\omega }_{f}}=\dfrac{15.7\times 30}{8} = 58.88rev/\min $ 

(b). Is kinetic energy conserved in the process? If not, from where does the change come about?

Ans: Kinetic energy is not conserved in the mentioned process. With the decrease in the moment of inertia, there is an increase in kinetic energy. The additional kinetic energy is generated from the work done by the man to fold his hands toward himself.

5. Read each statement below carefully, and state, with reasons, if it is true or false;

(a). During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.

Ans: False

Frictional force acts in the opposite direction of motion of the centre of mass of a body. In the case of rolling, the direct point of motion of the centre of mass is in backward direction. Therefore, frictional force acts in the forward direction.

(b). The instantaneous speed of the point of contact during rolling is zero.

Ans: True

Rolling can be considered as the rotation of a body about an axis that passes through the point of contact of the body with the ground. Therefore, its instantaneous speed is zero.

(c). The instantaneous acceleration of the point of contact during rolling is zero.

Ans: False

When a body is rolling, its instantaneous acceleration is not equal to zero. It has some value.

(d). For perfect rolling motion, work done against friction is zero.

Ans: True

When perfect rolling begins, the frictional force that acts at the lowermost point becomes zero. Therefore, the work done against friction is also zero.

(e). A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion.

Ans: True.

The rolling of a body occurs when a frictional force will act between the body and the surface. This frictional force will give the torque necessary for rolling. When the frictional force is not present, the body slips from the inclined plane under the effect of its own weight.

6. Two particles, each of mass $ m$ and speed $ v$ , travel in opposite directions along parallel lines separated by a distance $ d$ . Show that the vector angular momentum of the two-particle system is the same whatever be the point about which the angular momentum is taken.

Ans: Let us suppose that at a certain instant two particles be at points $ P$ and $ Q$ , as shown in the given figure.

Angular momentum of the system about point $ P$ can be given as:

$ \overrightarrow{{{L}_{P}}}=mv\times 0+mv\times d$ 

$ \Rightarrow \overrightarrow{{{L}_{P}}}=mvd$ …… (1)

Angular momentum of the system about point Q can be given as:

$ \overrightarrow{{{L}_{Q}}}=mv\times d+mv\times 0$ 

$ \Rightarrow \overrightarrow{{{L}_{Q}}}=mvd$ …… (2)

Let us consider a point $ R$ , which is at a distance $ y$ from point $ Q$ , i.e.,

$ QR=y$ 

$ \Rightarrow PR=d-y$ 

Angular momentum of the system about point $ R$ can be given as:

$ \overrightarrow{{{L}_{R}}}=mv\times \left( d-y \right)+mv\times y$ 

$ \Rightarrow \overrightarrow{{{L}_{R}}}=mvd-mvy+mvy$ 

$ \Rightarrow \overrightarrow{{{L}_{R}}}=mvd$ …… (3)

On comparing equations (1), (2), and (3), we get:

$ {{\overrightarrow{L}}_{P}}={{\overrightarrow{L}}_{Q}}={{\overrightarrow{L}}_{R}}$ …… (4)

We can hence infer from equation (4) that the angular momentum of a system is independent on the point about which it is taken.

Very Long Answer Questions (5 Marks)

1.

(a). Why is moment of inertia called rotational inertia?

Ans: Rotational inertia measures the moment of inertia during its rotational motion. Clearly, the moment of inertia is called rotational inertia.

(b). Calculate M.I of a uniform circular disc of mass $ 500gm$ and radius $ 10cm$ about 

(i) Diameter 

Ans: Moment of inertia can be given as:

$ {{I}_{d}}=\dfrac{1}{4}M{{R}^{2}}$ 

$ \Rightarrow {{I}_{d}}=\dfrac{1}{4}\times 500\times {{10}^{2}}=12500gmc{{m}^{2}}$ 

(ii) axis tangent to the disc and parallel to diameter

Ans: Moment of inertia can be given as:

$ {{I}_{d}}^{\prime }={{I}_{d}}+M{{R}^{2}}$ 

$ \Rightarrow {{I}_{d}}^{\prime }=\dfrac{1}{4}M{{R}^{2}}+M{{R}^{2}}$ 

$ \Rightarrow {{I}_{d}}^{\prime }=\dfrac{5}{4}M{{R}^{2}}$ 

$ \Rightarrow {{I}_{d}}^{\prime }=\dfrac{5}{4}\times 500\times {{10}^{2}}$ 

$ \Rightarrow {{I}_{d}}^{\prime }=62500gmc{{m}^{2}}$ 

(c). Axis passing through centre and perpendicular to its plane?

Ans: Moment of inertia can be calculated:

$ I=\dfrac{1}{2}M{{R}^{2}}$ 

$ \Rightarrow I=\dfrac{1}{2}\times 500\times {{\left( 10 \right)}^{2}}$ 

$ \Rightarrow I=25000gmc{{m}^{2}}$ 

2.

(a). A cat is able to land on its feet after a fall. Why?

Ans: When cat lands to the ground, it stretches its tail as a result of which, the moment of inertia increases.

Also, $ I\omega =cons\tan t$ 

Angular speed will be small because increase in moment of inertia and thus, the cat is able to land on its feet without any harm.

(b). If angular momentum moment of inertia is decreased, will its rotational be also conserved? Explain.

Ans: The moment of inertia of a system decreases from $ I$ to $ {I}'$ .

Then the angular speed will increase from $ \omega $ to $ {\omega }'$ .

We can write,

$ \Rightarrow I\omega ={I}'{\omega }'$ 

Since, $ \left( I\omega =constant \right)$ 

$ {\omega }'=\dfrac{I\omega }{{{I}'}}$ 

K.E. of rotation of the system can be given as

$ K.E.=\dfrac{1}{2}{I}'{{{\omega }'}^{2}}$ 

$ \Rightarrow K.E.=\dfrac{1}{2}{I}'{{\left( \dfrac{I\omega }{{{I}'}} \right)}^{2}}$ 

$ \Rightarrow K.E.=\dfrac{1}{2}\dfrac{{{I}^{2}}{{\omega }^{2}}}{{{I}'}}$ 

Therefore, because $ {I}'<I$ the K.E of the system will increase. Hence, the kinetic energy will not be conserved.

3. Find the components along the $ x$ , $ y$ , $ z$ axes of the angular momentum $ l$ of a particle, whose position vector is $ r$ with components $ x$ , $ y$ , $ z$ and momentum is $ p$ with components $ {{p}_{x}}$ , $ {{p}_{y}}$ and $ {{p}_{z}}$ . Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.

Ans: Linear momentum of the particle, $ \vec{p}={{p}_{x}}\hat{i}+{{p}_{y}}\hat{j}+{{p}_{z}}\hat{k}$ 

Position vector of the particle, $ \vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$ 

Angular momentum,

$ \vec{l}=\vec{r}\times \vec{p}$ 

$ \Rightarrow \vec{l}=\left( x\hat{i}+y\hat{j}+z\hat{k} \right)\times \left( {{p}_{x}}\hat{i}+{{p}_{y}}\hat{j}+{{p}_{z}}\hat{k} \right)$ 

$ \Rightarrow \vec{l}=\left( \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\ x & y & z \\ {{p}_{x}} & {{p}_{y}} & {{p}_{z}} \\ \end{matrix} \right)$

Now, 

$ {{l}_{x}}\hat{i}+{{l}_{y}}\hat{j}+{{l}_{z}}\hat{k}=\hat{i}\left( y{{p}_{z}}-z{{p}_{y}} \right)-\hat{j}\left( x{{p}_{z}}-z{{p}_{x}} \right)+k\left( x{{p}_{y}}-z{{p}_{x}} \right)$ 

On comparing the coefficients of $ \hat{i}$ , $ \hat{j}$ and $ \hat{k}$ , we can write:

$ {{l}_{x}}=y{{p}_{z}}-z{{p}_{y}}$ ,

$ {{l}_{y}}=z{{p}_{x}}-x{{p}_{z}}$ ,

$ {{l}_{z}}=x{{p}_{y}}-y{{p}_{x}}$ …… (1)

The particle is moving in the x-y plane. Therefore, the z-component of the position vector and linear momentum vector is becoming zero, i.e., $ z={{p}_{z}}=0$ 

Thus, equation (1) reduces to:

$ {{l}_{x}}=0$ 

$ {{l}_{y}}=0$ 

$ {{l}_{z}}=x{{p}_{y}}-y{{p}_{x}}$ 

Hence, when the particle is subject to move in the x-y plane, the direction of angular momentum will be along the z-direction. 

4. A non-uniform bar of weight $ W$ is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are $ 36.9{}^\circ $ and $ 53.1{}^\circ $ respectively. The bar is $ 2m$ long. Calculate the distance $ d$ of the centre of gravity of the bar from its left end.

Ans: The free body diagram of the bar can be drawn as shown in the given figure.

Length of the bar is given, $ l=2m$ 

$ {{T}_{1}}$ and $ {{T}_{2}}$ are the tensions generated in the left and right strings respectively.

At translational equilibrium, we can express:

$ {{T}_{1}}\sin 36.9{}^\circ ={{T}_{2}}\sin 53.1{}^\circ $ 

$ \Rightarrow \dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{\sin 53.1{}^\circ }{\sin 36.9{}^\circ }$ 

$ \Rightarrow \dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{0.800}{0.600}=\dfrac{4}{3}$ 

$ \Rightarrow {{T}_{1}}=\dfrac{4}{3}{{T}_{2}}$ 

On taking the torque about the centre of gravity, for rotational equilibrium, we can write:

$ {{T}_{1}}\cos 36.9{}^\circ \times d={{T}_{2}}\cos 53.1{}^\circ \left( 2-d \right)$ 

$ \Rightarrow {{T}_{1}}\times 0.800\times d={{T}_{2}}0.600\left( 2-d \right)$ 

$ \Rightarrow \dfrac{4}{3}\times {{T}_{2}}\times 0.800\times d={{T}_{2}}\left( 0.600\times 2-0.600d \right)$ 

$ \Rightarrow 1.067d+0.6d=1.2$ 

$ \Rightarrow d=\dfrac{1.2}{1.67}$ 

$ \Rightarrow d=0.72m$ 

Therefore, the centre of gravity of the given bar lies $ 0.72m$ from the left end of the bar.

5. A car weighs $ 1800kg$ . The distance between its front and back axles is $ 1.8m$. Its centre of gravity is $ 1.05m$ behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.

Ans: Given that,

Mass of the car is given as, $ m=1800kg$ 

Distance between the front and back axles, $ d=1.8m$ 

Distance between the centre of gravity and the back axle $ =1.05m$ 

The different forces acting on the car are shown in the given figure:

The forces in the figure, $ {{R}_{f}}$ and $ {{R}_{b}}$ are the forces exerted by the level ground on the front wheels and back wheels respectively.

At translational equilibrium we can write:

$ {{R}_{f}}+{{R}_{b}}=mg$ 

$ \Rightarrow {{R}_{f}}+{{R}_{b}}=1800\times 9.8$ 

$ \Rightarrow {{R}_{f}}+{{R}_{b}}=17640N$ …... (1)

For rotational equilibrium, on taking the torque about the centre of gravity, we can write:

$ {{R}_{f}}\left( 1.05 \right)={{R}_{b}}\left( 1.8-1.05 \right)$ 

$ \Rightarrow {{R}_{f}}\times \left( 1.05 \right)={{R}_{b}}\times \left( 0.75 \right)$ 

$ \Rightarrow \dfrac{{{R}_{f}}}{{{R}_{b}}}=\dfrac{0.75}{1.05}=\dfrac{5}{7}$ 

$ \Rightarrow \dfrac{{{R}_{b}}}{{{R}_{f}}}=\dfrac{7}{5}$ 

$ \Rightarrow {{R}_{b}}=1.4{{R}_{f}}$ …… (2)

Solving equations (1) and (2), we obtain:

$ 1.4{{R}_{f}}+{{R}_{f}}=17640N$ 

$ \Rightarrow {{R}_{f}}=\dfrac{17640}{2.4}N=7350N$ 

$ \Rightarrow {{R}_{b}}=\left( 17640-7350 \right)N=10290N$ 

Therefore, the force exerted on each front wheel can be given as $ \dfrac{7350}{2}N=3675N$ and 

the force exerted on each back wheel can be given as $ \dfrac{10290}{2}N=5145N$ .

6.

(a). Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be $ \dfrac{2M{{R}^{2}}}{5}$ where $ M$ is the mass of the sphere and $ R$ is the radius of the sphere.

Ans: The moment of inertia (M.I.) of a sphere about its diameter can be given as: $ \dfrac{2M{{R}^{2}}}{5}$ 

According to the theorem of parallel axes, the moment of inertia of a body about any axis is same as the sum of the moment of inertia of a certain body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.

The moment of inertia about a tangent of the sphere can be expressed as:

$ \dfrac{2M{{R}^{2}}}{5}+M{{R}^{2}}=\dfrac{7}{5}M{{R}^{2}}$ 

(b). Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be $ \dfrac{1}{4}M{{R}^{2}}$ , find its moment of inertia about an axis normal to the disc and passing through a point on its edge.

Ans: The moment of inertia of a disc about its diameter can be given as:$ \dfrac{1}{4}M{{R}^{2}}$ .

We can infer that, according to the theorem of perpendicular axis, the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is same as the sum of its moments of inertia about two perpendicular axes concurrent with perpendicular axis and lying in the plane of the body.

The moment of inertia of the disc about its centre is $ \dfrac{1}{4}M{{R}^{2}}+\dfrac{1}{4}M{{R}^{2}}=\dfrac{1}{2}M{{R}^{2}}$ 

The position of the perpendicular axis is shown in the following figure.

On application of the theorem of parallel axes:

The moment of inertia about an axis normal to the disc and passing through a point on its edge is $ \dfrac{1}{2}M{{R}^{2}}+M{{R}^{2}}=\dfrac{3}{2}M{{R}^{2}}$ .

7. Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?

Ans: Let us assume that $ m$ and $ r$ be the respective mass and radius of the hollow cylinder and the solid sphere. The moment of inertia of the hollow cylinder about its standard axis can be given as,

$ {{I}_{1}}=m{{r}^{2}}$ 

The moment of inertia of the solid sphere about an axis that passes through its centre can be given as,

$ {{I}_{2}}=\dfrac{2}{5}m{{r}^{2}}$ 

The formula for torque in terms of angular acceleration and moment of inertia can be expressed as:

$ \tau =I\alpha $ 

Where,

$ \tau =$ Torque

$ \alpha =$ Angular acceleration

$ I=$ Moment of inertia

For the hollow cylinder the expression can be given as,

$ {{\tau }_{1}}={{I}_{1}}{{\alpha }_{1}}$ 

For the solid sphere the expression can be given as,

$ {{\tau }_{2}}={{I}_{2}}{{\alpha }_{2}}$ 

As an equal amount of torque is applied to both the bodies it can be stated as, $ \dfrac{{{\alpha }_{2}}}{{{\alpha }_{1}}}=\dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{m{{r}^{2}}}{\dfrac{2}{5}m{{r}^{2}}}=\dfrac{2}{5}$ 

$ {{\alpha }_{2}}>{{\alpha }_{1}}$ …… (1)

Using the relation $ \omega ={{\omega }_{0}}+\alpha t$ 

Where,

$ \alpha =$ Angular acceleration 

$ t=$ Time of rotation

$ {{\omega }_{0}}=$ Initial angular velocity

$ \omega =$ Final angular velocity

For equal $ {{\omega }_{0}}$ and $ t$ , we have:

$ \omega =\alpha $ …... (2)

From equations (1) and (2), we can conclude:

$ {{\omega }_{2}}>{{\omega }_{1}}$ 

Therefore, the angular velocity ($ \omega $ ) of the solid sphere will be greater than that of the hollow cylinder.

8.

(a). A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of $ 40rev/\min $ . How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to $ \dfrac{2}{5}$ times the initial value? Assume that the turntable rotates without friction.

Ans: Given that,

Initial angular velocity of turntable, $ {{\omega }_{1}}=40rev/\min $ 

Final angular velocity of the given turntable is $ {{\omega }_{2}}$ 

The moment of inertia of the child with stretched hands can be given as $ {{I}_{1}}$ 

The moment of inertia of the child with folded hands can be given as $ {{I}_{2}}$ 

The two moments of inertia are related to each other as follows:

$ {{I}_{2}}=\dfrac{2}{5}{{I}_{1}}$ 

Since no external force acts on the child, the angular momentum $ L$ is not varying.

Therefore, for the two circumstances, we can write:

$ {{I}_{1}}{{\omega }_{1}}={{I}_{2}}{{\omega }_{2}}$ 

$ \Rightarrow {{\omega }_{2}}=\dfrac{{{I}_{1}}}{{{I}_{2}}}{{\omega }_{1}}$ 

$ \Rightarrow {{\omega }_{2}}=\dfrac{{{I}_{1}}}{\dfrac{2}{5}{{I}_{1}}}\times 40=\dfrac{5}{2}\times 40$ 

$ \Rightarrow {{\omega }_{2}}=100rev/\min $ 

(b). Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?

Ans: Given that,

Initial Kinetic energy of rotation of the turntable, $ {{E}_{i}}=\dfrac{1}{2}{{I}_{1}}{{\omega }^{2}}_{1}$ 

Final kinetic energy of rotation of the turntable, $ {{E}_{f}}=\dfrac{1}{2}{{I}_{2}}{{\omega }^{2}}_{2}$ 

$ \dfrac{{{E}_{f}}}{{{E}_{i}}}=\dfrac{\dfrac{1}{2}{{I}_{2}}{{\omega }^{2}}_{2}}{\dfrac{1}{2}{{I}_{1}}{{\omega }^{2}}_{1}}$ 

$ \Rightarrow \dfrac{{{E}_{f}}}{{{E}_{i}}}=\dfrac{\dfrac{1}{2}\times \dfrac{2}{5}\times {{I}_{1}}{{\omega }^{2}}_{2}}{\dfrac{1}{2}{{I}_{1}}{{\omega }^{2}}_{1}}$ 

$ \Rightarrow \dfrac{{{E}_{f}}}{{{E}_{i}}}=\dfrac{2}{5}\times \dfrac{{{\omega }^{2}}_{2}}{{{\omega }^{2}}_{1}}$ 

$ \Rightarrow \dfrac{{{E}_{f}}}{{{E}_{i}}}=\dfrac{2}{5}\times \dfrac{{{\left( 100 \right)}^{2}}}{{{\left( 40 \right)}^{2}}}$ 

$ \Rightarrow \dfrac{{{E}_{f}}}{{{E}_{i}}}=2.5$ 

$ \Rightarrow {{E}_{f}}=2.5\times {{E}_{i}}$ 

The increase in the rotational kinetic energy is related to the internal energy of the boy on the turntable.

9. From a uniform disc of radius $ R$ , a circular hole of radius $ \dfrac{R}{2}$ is cut out. The centre of the hole is at $ \dfrac{R}{2}$ from the centre of the original disc. Locate the centre of gravity of the resulting flat body.

Ans: Mass per unit area of the original disc can be given as $ \sigma $ .

Radius of the original disc $ =R$ 

Mass of the original disc,

$ M=\pi {{R}^{2}}\sigma $ 

The disc with the cut portion is shown in the given figure:

Radius of the smaller disc is given $ =\dfrac{R}{2}$ 

Mass of the smaller disc is given as $ {M}'=\pi {{\left( \dfrac{R}{2} \right)}^{2}}\sigma =\dfrac{1}{4}\pi {{R}^{2}}\sigma =\dfrac{M}{4}$ 

Let us suppose that $ O$ and $ {O}'$ be the respective centres of the original disc and the disc cut off from the original. As per definition of the centre of mass, the centre of mass of the original disc is assumed to be concentrated at $ O$ , while that of the smaller disc is assumed to be concentrated at $ {O}'$ .

It is provided that:

$ O{O}'=\dfrac{R}{2}$ 

After the smaller disc has been cut from the original disc, the remaining portion left over after cutting is considered to be a system of two masses. The two masses can be expressed as:

$ M\left( concentrated\,at\,O \right)-{M}'=\left( \dfrac{M}{4} \right)concentrated\,at\,{O}'$ 

(The negative sign in the above statement indicates that this portion has been removed from the original disc.)

Let us suppose that $ x$ be the distance through which the centre of mass of the remaining portion shifts from point $ O$ .

The relation between the centres of masses of two masses is given as:

$ x=\dfrac{{{m}_{1}}{{r}_{1}}+{{m}_{2}}{{r}_{2}}}{{{m}_{1}}+{{m}_{2}}}$ 

For the given system, it can be written as:

$ \Rightarrow x=\dfrac{M\times 0-{M}'\times \left( \dfrac{R}{2} \right)}{M+\left( -{M}' \right)}$ 

$ \Rightarrow x=\dfrac{\dfrac{-M}{4}\times \dfrac{R}{2}}{M-\dfrac{M}{4}}=\dfrac{-MR}{8}\times \dfrac{4}{3M}=\dfrac{-R}{6}$ 

(The negative sign in the above statement indicates that the centre of mass gets shifted toward the left of point $ O$ .)

The centre of gravity of the resulting flat body can be located from the original centre of the body and opposite to the centre of the cut portion.

10. A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. 

(a). Will it reach the bottom with the same speed in each case? 

Ans: Mass of the sphere $ =m$ 

Height of the plane $ =h$ 

Velocity of the sphere at the bottom of the plane is given as $ =v$ 

At the top of the plane, the total energy of the sphere i.e., Potential energy $ \left( P.E. \right)=mgh$ 

At the bottom of the plane, the sphere has both translational and rotational kinetic energies which can be expressed as,

Therefore, total energy $ T.E.=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}}$ 

Using the law of conservation of energy, we can state that:

$ \dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}}=mgh$ …… (1)

For a solid sphere, the moment of inertia about its centre can be given as,

$ I=\dfrac{2}{5}m{{r}^{2}}$ 

Therefore, equation (1) becomes:

$ \dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}\left( \dfrac{2}{5}m{{r}^{2}} \right){{\omega }^{2}}=mgh$ 

$ \Rightarrow \dfrac{1}{2}{{v}^{2}}+\left( \dfrac{1}{5}{{r}^{2}} \right){{\omega }^{2}}=gh$ 

But we have the formula,

$ v=r\omega $ 

$ \dfrac{1}{2}{{v}^{2}}+\dfrac{1}{5}{{v}^{2}}=gh$ 

$ \Rightarrow {{v}^{2}}\left( \dfrac{7}{10} \right)=gh$ 

$ \Rightarrow v=\sqrt{\dfrac{10}{7}gh}$ 

Therefore, the velocity of the sphere at the bottom depends only on height (h) and acceleration due to gravity (g). Both values are constants and do not change. Therefore, the velocity at the bottom remains the same from whichever inclined plane the sphere is rolled.

(b). Will it take longer to roll down one plane than the other? 

Ans: Let us consider two inclined planes with inclinations $ {{\theta }_{1}}$ and $ {{\theta }_{2}}$ respectively related as:

$ {{\theta }_{1}}<{{\theta }_{2}}$ 

The acceleration generated in the sphere when it rolls down the plane inclined at $ {{\theta }_{1}}$ is:

$ g\sin {{\theta }_{1}}$ 

The different forces acting on the sphere are shown in the given figure.

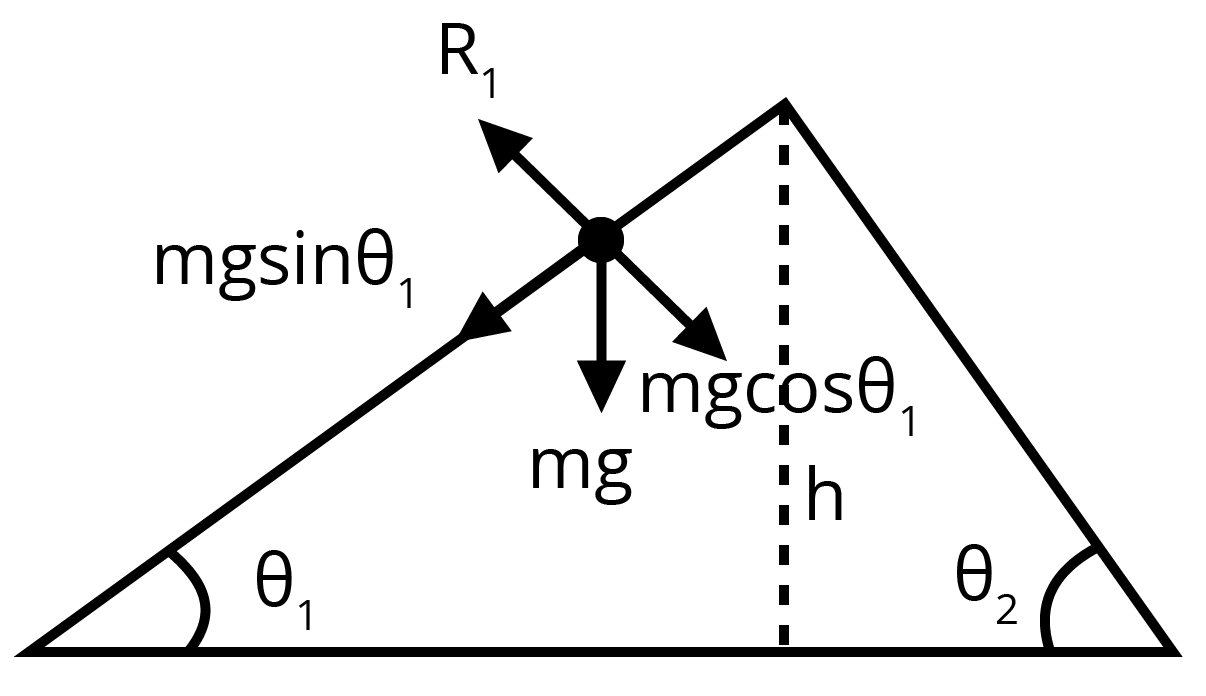
Here, $ R$ is the normal reaction to the sphere as shown in the above figure.

Similarly, the acceleration generated in the sphere when it rolls down the plane inclined at $ {{\theta }_{2}}$ is:

$ g\sin {{\theta }_{2}}$ 

The different forces that act on the sphere are shown in the given figure.

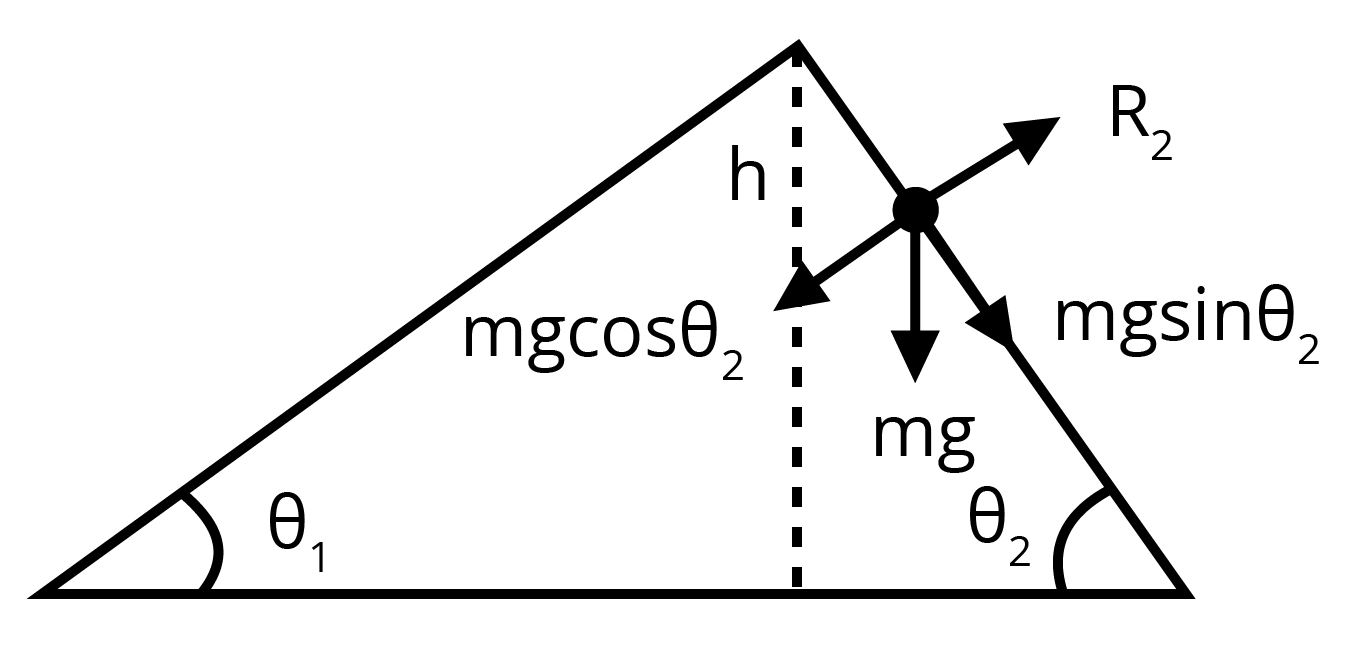
$ {{R}_{2}}$ is the normal reaction to the sphere as given in the figure.

$ {{\theta }_{1}}<{{\theta }_{2}}$ , $ \sin {{\theta }_{2}}>\sin {{\theta }_{1}}$ …… (1)

$ {{a}_{2}}>{{a}_{1}}$ …… (2)

Initial velocity of sphere, $ u=0$ 

Final velocity of sphere, $ v=$ constant

Now, by using the first equation of motion, we can obtain the time of roll as:

$ v=u+at$ 

$ t\propto \dfrac{1}{a}$ 

For inclination of angle $ {{\theta }_{1}}$ :

$ {{t}_{1}}\propto \dfrac{1}{{{a}_{1}}}$ 

For inclination of angle $ {{\theta }_{2}}$ :

$ {{t}_{2}}\propto \dfrac{1}{{{a}_{2}}}$ …… (3)

(c). If so, which one and why?

Ans: From equations (2) and (3), we obtain:

$ {{t}_{2}}<{{t}_{1}}$ 

Therefore, conclude that the sphere will take a longer time to reach the bottom of the inclined plane having the smaller inclination.

11. A solid cylinder rolls up an inclined plane of angle of inclination

$ 30{}^\circ $ . At the bottom of the inclined plane the centre of mass of the cylinder has a speed of $ 5m/s$ . How far will the cylinder go up the plane?

How long will it take to return to the bottom?

Ans: A solid cylinder rolling up an inclination is pictured in the following figure.

Initial velocity of the solid cylinder on the inclined plane, $ v=5m/s$ 

Angle of inclination is $ 30{}^\circ $ 

Height reached by the cylinder on the inclined plane $ =h$ 

Energy of the cylinder on the inclined plane at point $ A$ :

$ K{{E}_{rot}}=K{{E}_{trans}}$ 

$ \Rightarrow \dfrac{1}{2}I{{\omega }^{2}}=\dfrac{1}{2}m{{v}^{2}}$ 

Energy of the cylinder at point $ B$ $ =mgh$ 

Let us use the law of conservation of energy, we can express:

$ \dfrac{1}{2}I{{\omega }^{2}}=\dfrac{1}{2}m{{v}^{2}}=mgh$ 

Moment of inertia of the solid cylinder is $ I=\dfrac{1}{2}m{{r}^{2}}$ 

$ \Rightarrow \dfrac{1}{2}\left( \dfrac{1}{2}m{{r}^{2}} \right){{\omega }^{2}}+\dfrac{1}{2}m{{v}^{2}}=mgh$ 

$ \Rightarrow \dfrac{1}{4}m{{r}^{2}}{{\omega }^{2}}+\dfrac{1}{2}m{{v}^{2}}=mgh$ 

$ \Rightarrow \dfrac{1}{4}{{r}^{2}}{{\omega }^{2}}+\dfrac{1}{2}{{v}^{2}}=gh$ 

But we have the expression, $ v=r\omega $ 

$ \Rightarrow \dfrac{1}{4}{{v}^{2}}+\dfrac{1}{2}{{v}^{2}}=gh$ 

$ \Rightarrow \dfrac{3}{4}{{v}^{2}}=gh$ 

$ \Rightarrow h=\dfrac{3}{4}\times \dfrac{{{v}^{2}}}{g}$ 

$ \Rightarrow h=\dfrac{3}{4}\times \dfrac{5\times 5}{9.8}=1.91m$ 

In $ \Delta ABC$ , 

$ \sin \theta =\dfrac{BC}{AB}$ 

$ \Rightarrow \sin 30{}^\circ =\dfrac{h}{AB}$ 

$ AB=\dfrac{1.91}{0.5}=3.82m$ 

Therefore, the cylinder will move $ 3.82m$ up the inclined plane.

For radius of gyration $ K$ , the velocity of the cylinder at the instance when it rolls back to the bottom is given by the formula:

$ v={{\left( \dfrac{2gh}{1+\dfrac{{{K}^{2}}}{{{R}^{2}}}} \right)}^{\dfrac{1}{2}}}$ 

$ \Rightarrow v={{\left( \dfrac{2gAB\sin \theta }{1+\dfrac{{{K}^{2}}}{{{R}^{2}}}} \right)}^{\dfrac{1}{2}}}$ 

For the solid cylinder we can write $ {{K}^{2}}=\dfrac{{{R}^{2}}}{2}$ 

$ \Rightarrow v={{\left( \dfrac{2gAB\sin \theta }{1+\dfrac{1}{2}} \right)}^{\dfrac{1}{2}}}$ 

$ \Rightarrow v={{\left( \dfrac{4}{3}gAB\sin \theta \right)}^{\dfrac{1}{2}}}$ 

The time taken to return to the bottom can be given as:

$ t=\dfrac{AB}{v}$ 

$ \Rightarrow t=\dfrac{AB}{{{\left( \dfrac{4}{3}gAB\sin \theta \right)}^{\dfrac{1}{2}}}}$ 

$ \Rightarrow t={{\left( \dfrac{3AB}{4g\sin \theta } \right)}^{\dfrac{1}{2}}}$ 

$ \Rightarrow t={{\left( \dfrac{11.46}{19.6} \right)}^{\dfrac{1}{2}}}=0.764s$ 

Therefore, the total time taken by the cylinder to return to the bottom is $ \left( 2\times 0.764 \right)=1.53s$ 

12. As shown in figure, the two sides of a step ladder $ BA$ and $ CA$ are $ 1.6m$ long and hinged at $ A$ . A rope $ DE$ , $ 0.5m$ is tied halfway up. A weight $ 40kg$ is suspended from a point $ F$ , $ 1.2m$ from $ B$ along the ladder $ BA$ . Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take $ g=9.8m/{{s}^{2}}$ )

(Hint: Consider the equilibrium of each side of the ladder separately.)

Ans: The given situation can be depicted as follows:

$ {{N}_{B}}=$ Force exerted on the ladder by the floor point $ B$ 

$ {{N}_{C}}=$ Force exerted on the ladder by the floor point $ C$ 

$ T=$ Tension in the given rope 

$ BA=CA=1.6m$ 

$ DE=0.5m$ 

$ BF=1.2m$ 

Mass of the given weight, $ m=40kg$ 

Draw a perpendicular line from $ A$ on the floor $ BC$ . This line intersects $ DE$ at mid-point $ H$ .

In $ \Delta ABI$ and $ \Delta AIC$ are similar

$ BI=IC$ 

Therefore, $ I$ is the mid-point of $ BC$ .

$ DE\parallel BC$ 

$ BC=2\times DE=1m$ 

$ AF=BA-BF=0.4m$ …… (1)

It can be said that $ D$ is the mid-point of AB.

Therefore, we can express:

$ AD=\dfrac{1}{2}\times BA=0.8m$ ……. (2)

Using equations (1) and (2), we get:

$ FE=0.4m$ 

Therefore, $ F$ is the mid-point of $ AD$ .

$ FG\parallel DH$ and $ F$ is the mid-point of $ AD$ . Therefore, $ G$ will also be the mid-point of $ AH$ .

$ \Delta AFG$ and $ \Delta ADH$ are similar triangles.

$ \dfrac{FG}{DH}=\dfrac{AF}{AD}$ 

$ \Rightarrow \dfrac{FG}{DH}=\dfrac{0.4}{0.8}=\dfrac{1}{2}$ 

$ \Rightarrow FG=\dfrac{1}{2}DH$ 

$ \Rightarrow FG=\dfrac{1}{2}\times 0.25=0.125m$ 

In $ \Delta ADH$ we can state,

$ AH=\sqrt{A{{D}^{2}}-D{{H}^{2}}}$ 

$ \Rightarrow AH=\sqrt{{{0.8}^{2}}-{{0.25}^{2}}}=0.75m$ 

For translational equilibrium of the ladder, the upward force should be the same as the downward force.

$ {{N}_{C}}+{{N}_{B}}=mg=392$ …… (3)

For rotational equilibrium of the ladder, the net moment about A can be given as:

$ \Rightarrow -{{N}_{B}}\times 0.5+40\times 9.8\times 0.125+{{N}_{C}}\times 0.5=0$ 

$ \Rightarrow \left( {{N}_{C}}-{{N}_{B}} \right)\times 0.5=49$ 

$ \Rightarrow {{N}_{C}}-{{N}_{B}}=98$ …… (4)

Solving equations (3) and (4), we can write:

$ {{N}_{C}}=245N$ 

$ {{N}_{B}}=147N$ 

For rotational equilibrium of the side AB, let us consider the moment about A.

$ -{{N}_{B}}\times BI+mg\times FG+T\times AG=0$ 

$ \Rightarrow -245\times 0.5+40+9.8\times 0.125+T\times 0.76=0$ 

$ \Rightarrow 0.76T=122.5-49$ 

$ \Rightarrow T=96.7N$ , which is the required tension.

13. Two discs of moments of inertia $ {{I}_{1}}$ and $ {{I}_{2}}$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds $ {{\omega }_{1}}$ and $ {{\omega }_{2}}$ are brought into contact face to face with their axes of rotation coincident.

(a). What is the angular speed of the two-disc system? 

Ans: Given that,

Moment of inertia of disc 1 is $ {{I}_{1}}$ 

Angular speed of disc 1 is $ {{\omega }_{1}}$ 

Moment of inertia of disc 2 is $ {{I}_{2}}$ 

Angular speed of disc 2 is $ {{\omega }_{2}}$ 

Angular momentum of disc 1 is $ {{L}_{1}}={{I}_{1}}{{\omega }_{1}}$ 

Angular momentum of disc 2 is $ {{L}_{2}}={{I}_{2}}{{\omega }_{2}}$ 

Total initial angular momentum is $ {{L}_{i}}={{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}}$ 

When the two discs are joined together, their moments of inertia get summed up.

Moment of inertia of the system of two discs can be given as,

$ I={{I}_{1}}+{{I}_{2}}$ 

Let $ \omega $ be the angular speed of the system.

Total final angular momentum is given as, $ {{L}_{f}}=\left( {{I}_{1}}+{{I}_{2}} \right)\omega $ 

Let us use the law of conservation of angular momentum,

$ {{L}_{i}}={{L}_{f}}$ 

$ \Rightarrow {{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}}=\left( {{I}_{1}}+{{I}_{2}} \right)\omega $ 

$ \Rightarrow \omega =\dfrac{{{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}}}{{{I}_{1}}+{{I}_{2}}}$ , which is the required angular speed.

(b). Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take $ {{\omega }_{1}}\ne {{\omega }_{2}}$ .

Ans: Given that,

Kinetic energy of disc 1 is given as, $ {{E}_{1}}=\dfrac{1}{2}{{I}_{1}}{{\omega }^{2}}_{1}$ 

Kinetic energy of disc 2, $ {{E}_{2}}=\dfrac{1}{2}{{I}_{2}}{{\omega }^{2}}_{2}$ 

Total initial kinetic energy can be given as, $ {{E}_{i}}=\dfrac{1}{2}\left( {{I}_{1}}{{\omega }^{2}}_{1}+{{I}_{2}}{{\omega }^{2}}_{2} \right)$ 

When the discs are joined, their moments of inertia get summed up.

Moment of inertia of the system can be given as, $ I={{I}_{1}}+{{I}_{2}}$ 

Angular speed of the system can be given as: $ \omega $ 

Final kinetic energy $ {{E}_{f}}=\dfrac{1}{2}\left( {{I}_{1}}+{{I}_{2}} \right){{\omega }^{2}}$ 

$ \Rightarrow {{E}_{f}}=\dfrac{1}{2}\left( {{I}_{1}}+{{I}_{2}} \right){{\left( \dfrac{{{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}}}{{{I}_{1}}+{{I}_{2}}} \right)}^{2}}=\dfrac{1}{2}\times \dfrac{{{\left( {{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}} \right)}^{2}}}{{{I}_{1}}+{{I}_{2}}}$ 

And $ {{E}_{i}}={{E}_{f}}$ 

$ \Rightarrow {{E}_{i}}=\dfrac{1}{2}\left( {{I}_{1}}{{\omega }^{2}}_{1}+{{I}_{2}}{{\omega }^{2}}_{2} \right)-\dfrac{{{\left( {{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}} \right)}^{2}}}{2\left( {{I}_{1}}+{{I}_{2}} \right)}$ 

$ \Rightarrow {{E}_{i}}=\dfrac{1}{2}{{I}_{1}}{{\omega }^{2}}_{1}+\dfrac{1}{2}{{I}_{2}}{{\omega }^{2}}_{2}-\dfrac{1}{2}\dfrac{{{I}^{2}}_{1}{{\omega }^{2}}_{1}}{\left( {{I}_{1}}+{{I}_{2}} \right)}-\dfrac{1}{2}\dfrac{{{I}^{2}}_{2}{{\omega }^{2}}_{2}}{\left( {{I}_{1}}+{{I}_{2}} \right)}-\dfrac{1}{2}\dfrac{2{{I}_{1}}{{I}_{2}}{{\omega }_{1}}{{\omega }_{2}}}{\left( {{I}_{1}}+{{I}_{2}} \right)}$ 

$ \Rightarrow {{E}_{i}}=\dfrac{1}{\left( {{I}_{1}}+{{I}_{2}} \right)}\left[ \dfrac{1}{2}{{I}_{2}}{{\omega }^{2}}_{1}+\dfrac{1}{2}{{I}_{1}}{{I}_{2}}{{\omega }^{2}}_{1}+\dfrac{1}{2}{{I}_{1}}{{I}_{2}}{{\omega }^{2}}_{2}+\dfrac{1}{2}{{I}_{2}}{{\omega }^{2}}_{2}-\dfrac{1}{2}{{I}_{1}}{{\omega }^{2}}_{1}-\dfrac{1}{2}{{I}_{2}}{{\omega }^{2}}_{2}-{{I}_{1}}{{I}_{2}}{{\omega }_{1}}{{\omega }_{1}} \right]$ 

$ \Rightarrow {{E}_{i}}=\dfrac{{{I}_{1}}{{I}_{2}}}{2\left( {{I}_{1}}+{{I}_{2}} \right)}\left( {{\omega }_{1}}^{2}+{{\omega }^{2}}_{2}-2{{\omega }_{1}}{{\omega }_{2}} \right)$ 

$ \Rightarrow {{E}_{i}}=\dfrac{{{I}_{1}}{{I}_{2}}{{\left( {{\omega }_{1}}-{{\omega }_{2}} \right)}^{2}}}{2\left( {{I}_{1}}+{{I}_{2}} \right)}$ 

All the quantities on right hand side are positive

$ {{E}_{i}}-{{E}_{f}}>0$ 

$ {{E}_{i}}>{{E}_{f}}$ 

The loss of K.E. can be attributed to the frictional force that comes into play when the two discs come in contact with each other.

14. 

(a). Prove the theorem of perpendicular axes. (Hint: Square of the distance of a point $ \left( x,y \right)$ in the x–y plane from an axis through the origin perpendicular to the plane is $ {{x}^{2}}+{{y}^{2}}$ ) 

Ans: It is stated by the theorem of perpendicular axes states that the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with perpendicular axis and lying in the plane of the body.

A physical body with centre $ O$ and a point mass $ m$ , in the x–y plane at (x, y) is shown in the following figure.

Moment of inertia about x-axis can be given as, $ {{I}_{x}}=m{{x}^{2}}$ 

Moment of inertia about y-axis can be given as, $ {{I}_{y}}=m{{y}^{2}}$ 

Moment of inertia about z-axis can be given as, $ {{I}_{z}}=m{{\left( \sqrt{{{x}^{2}}+{{y}^{2}}} \right)}^{2}}$ 

$ {{I}_{x}}+{{I}_{y}}=m{{x}^{2}}+m{{y}^{2}}=m\left( {{x}^{2}}+{{y}^{2}} \right)$ 

$ \Rightarrow {{I}_{x}}+{{I}_{y}}=m{{\left( \sqrt{{{x}^{2}}+{{y}^{2}}} \right)}^{2}}$ 

$ \Rightarrow {{I}_{x}}+{{I}_{y}}={{I}_{z}}$ 

Therefore, the theorem is proved.

(b). Prove the theorem of parallel axes.

(Hint: If the centre of mass is chosen to be the origin $ \sum{{{m}_{i}}{{r}_{i}}=0}$ )

Ans: The theorem of parallel axes states that the moment of inertia of a body about any axis is same as the sum of the moment of inertia of the body about a parallel axis that passes through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.

Let us suppose that a rigid body is made up of $ n$ particles, having masses at $ {{m}_{1}},{{m}_{2}},{{m}_{3}},...,{{m}_{n}}$ perpendicular distances $ {{r}_{1}},{{r}_{2}},{{r}_{3}},...,{{r}_{n}}$ respectively from the centre of mass $ O$ of the rigid body.

The moment of inertia about axis $ RS$ passing through the point $ O$ can be given as:

$ {{I}_{RS}}=\sum_{i=1}^{n}{{{m}_{i}}{{r}_{i}}^{2}}$ 

The perpendicular distance of mass $ {{m}_{i}}$ , from the axis

$ QP=a+{{r}_{i}}$ 

Therefore, the moment of inertia about axis $ QP$ can be given as:

$ {{I}_{QP}}=\sum\limits_{i=1}^{n}{{{m}_{i}}{{\left( a+{{r}_{i}} \right)}^{2}}}$ 

$ \Rightarrow {{I}_{QP}}=\sum\limits_{i=1}^{n}{{{m}_{i}}\left( {{a}^{2}}+{{r}^{2}}_{i}+2a{{r}_{i}} \right)}$ 

$ \Rightarrow {{I}_{QP}}=\sum\limits_{i=1}^{n}{{{m}_{i}}\left( {{a}^{2}} \right)+}\sum\limits_{i=1}^{n}{{{m}_{i}}{{r}^{2}}_{i}+}\sum\limits_{i=1}^{n}{{{m}_{i}}2a{{r}_{i}}}$ 

$ \Rightarrow {{I}_{QP}}={{I}_{RS}}+\sum\limits_{i=1}^{n}{{{m}_{i}}\left( {{a}^{2}} \right)+}2\sum\limits_{i=1}^{n}{{{m}_{i}}a{{r}_{i}}}$ 

Now, at the centre of mass, the moment of inertia of all the particles about the axis that passes through the centre of mass is zero, that is,

$ 2\sum\limits_{i=1}^{n}{{{m}_{i}}a{{r}_{i}}}=0$ 

Where, $ a\ne 0$ 

$ \sum{{{m}_{i}}{{r}_{i}}=0}$ 

$ \sum\limits_{i=1}^{n}{{{m}_{i}}}=M$ 

$ M=$ Total mass of the rigid body

$ {{I}_{QP}}={{I}_{RS}}+M{{a}^{2}}$ 

Therefore, the theorem is proved.

15. Prove the result that the velocity $ v$ of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height $ h$ is given by $ {{v}^{2}}=\dfrac{2gh}{\left( 1+\dfrac{{{k}^{2}}}{{{R}^{2}}} \right)}$ using dynamical consideration (i.e., by consideration of forces and torques). Note $ k$ is the radius of gyration of the body about its symmetry axis, and $ R$ is the radius of the body. The body starts from rest at the top of the plane.

Ans: A body rolling on an inclined plane of height h, is depicted in the given figure:

$ m=$ Mass of the body

$ R=$ Radius of the body

$ K=$ Radius of gyration of the body

$ v=$ Translational velocity of the body

$ h=$ Height of the inclined plane

$ g=$ Acceleration due to gravity

Total energy at the top of the plane is given as,

$ {{E}_{1}}=mgh$ 

Total energy at the bottom of the plane can be given as,

$ {{E}_{b}}=K{{E}_{rot}}+K{{E}_{trans}}$ 

$ \Rightarrow {{E}_{b}}=\dfrac{1}{2}I{{\omega }^{2}}+\dfrac{1}{2}m{{v}^{2}}$ 

But $ I=m{{k}^{2}}$ and $ \omega =\dfrac{v}{R}$ 

$ \Rightarrow {{E}_{b}}=\dfrac{1}{2}m{{k}^{2}}\left( \dfrac{{{v}^{2}}}{{{R}^{2}}} \right)+\dfrac{1}{2}m{{v}^{2}}$ 

$ \Rightarrow {{E}_{b}}=\dfrac{1}{2}m{{v}^{2}}\dfrac{{{k}^{2}}}{{{R}^{2}}}+\dfrac{1}{2}m{{v}^{2}}$ 

$ \Rightarrow {{E}_{b}}=\dfrac{1}{2}m{{v}^{2}}\left( 1+\dfrac{{{k}^{2}}}{{{R}^{2}}} \right)$ 

From the law of conservation of energy, we can write:

$ {{E}_{T}}={{E}_{B}}$ 

$ \Rightarrow mgh=\dfrac{1}{2}m{{v}^{2}}\left( 1+\dfrac{{{k}^{2}}}{{{R}^{2}}} \right)$ 

$ \Rightarrow v=\dfrac{2gh}{\left( 1+\dfrac{{{k}^{2}}}{{{R}^{2}}} \right)}$ 

Therefore, the given result is proved.

16. A disc rotating about its axis with angular speed $ {{\omega }_{0}}$ is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is $ R$ . What are the linear velocities of the points $ A$ , $ B$ and $ C$ on the disc shown in figure? Will the disc roll in the direction indicated?

Ans: From the question we can infer that:

$ {{v}_{A}}=R{{\omega }_{0}}$ ,

$ {{v}_{B}}=R{{\omega }_{0}}$ ,

$ {{v}_{C}}=\left( \dfrac{R}{2} \right){{\omega }_{0}}$ 

The rolling of the disc will not take place.

Angular speed of the disc is given $ ={{\omega }_{0}}$ 

Radius of the disc is given $ =R$ 

Let us use the relation for linear velocity, $ v={{\omega }_{0}}R$ 

For point A we can write:

$ {{v}_{A}}=R{{\omega }_{0}}$ in the direction tangential to the right

For point B we can write:

$ {{v}_{B}}=R{{\omega }_{0}}$ in the direction tangential to the left

For point C it can be written as:

$ {{v}_{C}}=\left( \dfrac{R}{2} \right){{\omega }_{0}}$ in the direction same as that of $ {{v}_{A}}$ .

The directions of motion of points $ A$ , $ B$ , and $ C$ on the disc are depicted in the following figure:

Because the disc is placed on a frictionless table, the disc will not roll. This is due to the presence of friction, which is essential for the rolling of a body.

17. A solid disc and a ring, both of radius $ 10cm$ are placed on a horizontal table simultaneously, with initial angular speed equal to $ 10\pi \,rad\,{{s}^{-1}}$ . Which of the two will start to roll earlier? The co-efficient of kinetic friction is

$ {{\mu }_{k}}=0.2$ .

Ans: Given that,

Radii of the ring and the disc are given as, r = 10 cm = 0.1 m

Initial angular speed is given, $ u=0$ 

Coefficient of kinetic friction is, $ {{\mu }_{k}}=0.2$ 

Initial velocity of both the objects, $ u=0$ 

Motion of the two objects is a result of frictional force. As per Newton’s second law of motion,

we have frictional force, $ f=ma$ 

$ {{\mu }_{k}}mg=ma$ 

Where,

$ a=$ Acceleration produced in the objects

$ m=$ Mass

$ a={{\mu }_{k}}g$ …… (1)

From the first equation of motion, the final velocity of the objects can be obtained as:

$ v=u+at$ 

$ \Rightarrow v=0+{{\mu }_{k}}gt$ 

$ v={{\mu }_{k}}gt$ …... (2)

The torque applied by the frictional force will act in perpendicularly outward direction and cause reduction in the initial angular speed.

Torque, $ \tau =-I\alpha $ 

$ \alpha =$ Angular acceleration

$ {{\mu }_{k}}mgr=-I\alpha $ 

$ \Rightarrow \alpha =\dfrac{-{{\mu }_{k}}mgr}{I}$ …… (3)

Let us use the first equation of rotational motion to obtain the final angular speed:

$ \omega ={{\omega }_{0}}+\alpha t$ 

$ \Rightarrow \omega ={{\omega }_{0}}+\dfrac{-{{\mu }_{k}}mgr}{I}t$ …… (4)

Rolling starts when linear velocity, $ v=r\omega $ 

$ v=r\left( {{\omega }_{0}}-\dfrac{{{\mu }_{k}}mgrt}{I} \right)$ …… (5)

Equating equations (2) and (5), we can write:

$ {{\mu }_{k}}gt=r\left( {{\omega }_{0}}-\dfrac{{{\mu }_{k}}mgrt}{I} \right)$ 

$ \Rightarrow {{\mu }_{k}}gt=r\left( {{\omega }_{0}}-\dfrac{{{\mu }_{k}}mgrt}{I} \right)$ …… (6)

For the ring:

$ I=m{{r}^{2}}$ 

$ {{\mu }_{k}}gt=r\left( {{\omega }_{0}}-\dfrac{{{\mu }_{k}}mgrt}{m{{r}^{2}}} \right)$ 

$ {{\mu }_{k}}gt=r{{\omega }_{0}}-{{\mu }_{k}}gt$ 

$ \Rightarrow 2{{\mu }_{k}}gt=r{{\omega }_{0}}$ 

$ \Rightarrow {{t}_{r}}=\dfrac{r{{\omega }_{0}}}{2{{\mu }_{k}}g}$ 

$ \Rightarrow {{t}_{r}}=\dfrac{0.1\times 10\times 3.14}{2\times 0.2\times 9.8}=0.80s$ …… (7)

For the disc:

$ I=\dfrac{1}{2}m{{r}^{2}}$ 

$ {{\mu }_{k}}g{{t}_{d}}=r{{\omega }_{0}}-\dfrac{{{\mu }_{k}}gm{{r}^{2}}{{t}_{d}}}{\dfrac{1}{2}m{{r}^{2}}}$ 

$ \Rightarrow {{\mu }_{k}}g{{t}_{d}}=r{{\omega }_{0}}-\dfrac{{{\mu }_{k}}g{{t}_{d}}}{\dfrac{1}{2}}$ 

$ \Rightarrow {{\mu }_{k}}g{{t}_{d}}=r{{\omega }_{0}}-2{{\mu }_{k}}g{{t}_{d}}$ 

$ \Rightarrow 3{{\mu }_{k}}g{{t}_{d}}=r{{\omega }_{0}}$ 

$ {{t}_{d}}=\dfrac{r{{\omega }_{0}}}{3{{\mu }_{k}}g}$ 

$ \Rightarrow {{t}_{d}}=\dfrac{0.1\times 10\times 3.14}{3\times 0.2\times 9.8}=0.53s$ …… (8)

Since, $ {{t}_{d}}>{{t}_{r}}$ the disc will start rolling before the ring.

18. A cylinder of mass $ 10kg$ and radius $ 15cm$ is rolling perfectly on a plane of inclination $ 30{}^\circ $ . The coefficient of static friction $ {{\mu }_{k}}=0.25$ 

(a). How much is the force of friction acting on the cylinder?

Ans: Given that,

Mass of the cylinder is given as, $ m=10kg$ 

Radius of the cylinder is given as, $ r=15cm=0.15m$ 

Co-efficient of kinetic friction $ {{\mu }_{k}}=0.25$ 

Angle of inclination is given as, $ \theta =30{}^\circ $ 

Moment of inertia of a solid cylinder about its geometric axis is,

$ I=\dfrac{1}{2}m{{r}^{2}}$ 

The various forces acting on the cylinder are depicted in the given figure:

The acceleration of the cylinder is given as:

$ a=\dfrac{mg\sin \theta }{m+\dfrac{I}{{{r}^{2}}}}$ 

$ \Rightarrow a=\dfrac{mg\sin \theta }{m+\dfrac{m{{r}^{2}}}{2{{r}^{2}}}}=\dfrac{2}{3}g\sin 30{}^\circ $ 

$ \Rightarrow a=\dfrac{2}{3}\times 9.8\times 0.5=3.27m/{{s}^{2}}$ 

Let us use Newton’s second law of motion, we can express net force as:

$ {{f}_{net}}=ma$ 

$ mg\sin 30{}^\circ -f=ma$ 

$ \Rightarrow f=mg\sin 30{}^\circ -ma$ 

$ \Rightarrow f=10\times 9.8\times 0.5-10\times 3.27$ 

$ \Rightarrow f=49-32.7=16.3N$ 

(b). What is the work done against friction during rolling?

Ans: During rolling, the instantaneous point of contact with the plane will come to rest. Therefore, the work done against frictional force will be zero.

(c). If the inclination of the plane is increased, at what value of does the cylinder begin to skid, and not roll perfectly?

Ans: For rolling without skidding, we have the formula:

$ \mu =\dfrac{1}{3}\tan \theta $ 

$ \Rightarrow \tan \theta =3\mu =3\times 0.25=0.75$ 

$ \Rightarrow {{\tan }^{-1}}0.75=36.87{}^\circ $ 

19. Separation of motion of a system of particles into motion of the centre of mass and motion about the centre of mass:

(a). Show $ {{p}_{i}}={{p}_{i}}^{\prime }+{{m}_{i}}V$ Where $ {{p}_{i}}$ is the momentum of the $ {{i}^{th}}$ particle (of mass$ {{m}_{i}}$ ) and $ {{p}_{i}}^{\prime }={{m}_{i}}{{v}_{i}}^{\prime }$ . Note $ {{v}_{i}}^{\prime }$ is the velocity of the $ {{i}^{th}}$ particle relative to the centre of mass. Also, prove using the definition of the centre of mass $ \sum\limits_{i}{{{p}_{i}}^{\prime }}=0$ . 

Ans: Let us take a system of $ i$ moving particles.

Mass of the $ {{i}^{th}}$ particle $ ={{m}_{i}}$ 

Velocity of the $ {{i}^{th}}$ particle $ ={{v}_{i}}$ 

Therefore, momentum of the $ {{i}^{th}}$ particle, $ {{p}_{i}}={{m}_{i}}{{v}_{i}}$ 

Velocity of the centre of mass is $ V$ 

The velocity of the $ {{i}^{th}}$ particle with respect to the centre of mass of the system is given as: $ {{v}_{i}}^{\prime }={{v}_{i}}-V$ …… (1)

Multiplying $ {{m}_{i}}$ throughout equation (1),

we can write: 

$ {{m}_{i}}{{v}_{i}}^{\prime }={{m}_{i}}{{v}_{i}}-{{m}_{i}}V$ 

$ {{p}_{i}}^{\prime }={{p}_{i}}-{{m}_{i}}V$ 

Where,

$ {{p}_{i}}^{\prime }={{m}_{i}}{{v}_{i}}^{\prime }$ is the Momentum of the $ {{i}^{th}}$ particle with respect to the centre of mass of the system.

Hence, $ {{p}_{i}}={{p}_{i}}^{\prime }+{{m}_{i}}V$ 

We have the formula: $ {{p}_{i}}^{\prime }={{m}_{i}}{{v}_{i}}^{\prime }$ 

Taking the summation of momentum of all the particles with respect to the centre of mass of the system, we can write:

$ \sum\limits_{i}{{{p}_{r}}^{\prime }}=\sum\limits_{i}{{{m}_{i}}}{{v}_{i}}^{\prime }=\sum\limits_{i}{{{m}_{i}}}\dfrac{d{{r}_{i}}^{\prime }}{dt}$ 

Where

$ {{r}_{i}}^{\prime }$ is the position vector of $ {{i}^{th}}$ particle with respect to the centre of mass

$ {{v}_{i}}^{\prime }=\dfrac{d{{r}_{i}}^{\prime }}{dt}$ 

As per the definition of the centre of mass, we have:

$ \sum\limits_{i}{{{m}_{i}}}{{v}_{i}}^{\prime }=0$ 

$ \Rightarrow \sum\limits_{i}{{{m}_{i}}}\dfrac{d{{r}_{i}}^{\prime }}{dt}=0$ 

$ \Rightarrow \sum\limits_{i}{{{p}_{i}}^{\prime }}=0$ 

(b). Show $ K={K}'+\dfrac{1}{2}M{{V}^{2}}$ , where $ K$ is the total kinetic energy of the system of particles, $ {K}'$ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and $ \dfrac{1}{2}M{{V}^{2}}$ is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.

Ans: We have the formula for velocity of the $ {{i}^{th}}$ particle as:

$ {{v}_{i}}={{v}_{i}}^{\prime }+V$ 

$ \sum{{{m}_{i}}{{v}_{i}}=\sum{{{m}_{i}}{{v}_{i}}^{\prime }}}+\sum{{{m}_{i}}V}$ 

Taking the dot product of equation (2) with itself, we can write:

$ \sum\limits_{i}{{{m}_{i}}{{v}_{f}}}\sum\limits_{i}{{{m}_{i}}{{v}_{i}}^{\prime }}+\sum\limits_{i}{{{m}_{i}}\left( {{v}_{f}}^{\prime }+V \right)}\sum\limits_{i}{{{m}_{i}}\left( {{v}_{i}}^{\prime }+v \right)}$ 

$ {{M}^{2}}\sum\limits_{i}{{{v}_{i}}^{2}={{M}^{2}}}\sum\limits_{i}{{{v}_{i}}^{2}}+{{M}^{2}}\sum\limits_{i}{{{v}_{i}}{{v}_{i}}^{\prime }+{{M}^{2}}}\sum\limits_{i}{{{v}_{i}}^{\prime }{{v}_{i}}+{{M}^{2}}{{V}^{2}}}$ 

Now, for the centre of mass of the system of particles, $ \sum\limits_{i}{{{v}_{i}}^{\prime }{{v}_{i}}}=-\sum\limits_{i}{{{v}_{i}}^{\prime }{{v}_{i}}}$ ,

$ {{M}^{2}}\sum\limits_{i}{{{v}_{1}}^{2}={{M}^{2}}\sum\limits_{i}{{{v}_{1}}^{2}}+{{M}^{2}}{{V}^{2}}}$ 

$ \dfrac{1}{2}M\sum\limits_{i}{{{v}_{1}}^{2}=\dfrac{1}{2}M\sum\limits_{i}{{{{{v}'}}_{1}}^{2}}+\dfrac{1}{2}M{{V}^{2}}}$ 

$ K={K}'+\dfrac{1}{2}M{{V}^{2}}$ 

Where,

$ K=\dfrac{1}{2}M\sum\limits_{i}{{{v}_{1}}^{2}}$ is the total kinetic energy of the system of particles

$ {K}'=\dfrac{1}{2}M\sum\limits_{i}{{{{{v}'}}_{1}}^{2}}$ is the total kinetic energy of the system of particles with respect to the centre of mass

$ \dfrac{1}{2}M{{V}^{2}}$ is the Kinetic energy of the translation of the system as a whole.

(c). Show $ L={L}'+R\times MV$ Where $ {L}'=\sum{{{r}_{i}}^{\prime }}\times {{p}_{i}}^{\prime }$ is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember $ {{r}_{i}}^{\prime }={{r}_{i}}-R$ rest of the notation is the standard notation used in the chapter. Note $ {L}'$ and $ R\times MV$ can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.

Ans: Position vector of the $ {{i}^{th}}$ particle with respect to origin can be given $ ={{r}_{i}}$ 

Position vector of the $ {{i}^{th}}$ particle with respect to the centre of mass is given $ ={{{r}'}_{i}}$ 

With respect to the origin the position vector of the centre of mass $ =R$ 

It is provided that:

$ {{{r}'}_{i}}={{r}_{i}}-R$ 

$ {{r}_{i}}={{{r}'}_{i}}+R$ 

We have the following relation from part (a),

$ {{p}_{i}}={{{p}'}_{i}}+{{m}_{i}}V$ 

Taking the cross product of this relation by $ {{r}_{i}}$ we can write:

$ \sum\limits_{i}{{{r}_{i}}\times {{p}_{i}}}=\sum\limits_{i}{{{r}_{i}}\times {{{{p}'}}_{i}}}=\sum\limits_{i}{{{r}_{i}}\times {{m}_{i}}V}$ 

$ L=\sum\limits_{i}{\left( {{r}_{i}}\times R \right)\times {{{{p}'}}_{i}}}+\sum\limits_{i}{\left( {{{{r}'}}_{i}}\times R \right)\times {{m}_{i}}V}$ 

$ \Rightarrow L=\sum\limits_{i}{{{{{r}'}}_{i}}\times {{{{p}'}}_{i}}}+\sum\limits_{i}{R\times {{{{p}'}}_{i}}+\sum\limits_{i}{{{{{r}'}}_{i}}\times {{m}_{i}}V}+\sum\limits_{i}{R\times {{m}_{i}}V}}$ 

$ \Rightarrow L={L}'+\sum\limits_{i}{{{R}_{i}}\times {{{{p}'}}_{i}}}+\sum\limits_{i}{{{{{r}'}}_{i}}\times {{m}_{i}}V}+\sum\limits_{i}{R\times {{m}_{i}}V}$ 

where,

$ R\times \sum\limits_{i}{{{{{p}'}}_{i}}}=0$ and $ \left( \sum\limits_{i}{{{{{r}'}}_{i}}} \right)\times MV=0$ 

Hence, $ \sum\limits_{i}{{{m}_{i}}}=M$ 

$ \Rightarrow L={L}'+R\times MV$ 

(c). Show $ \dfrac{d{L}'}{dt}=\sum\limits_{i}{{{r}_{i}}^{\prime }\times }\dfrac{d}{dt}\left( {{P}_{i}}^{\prime } \right)$ . Further, show that $ \dfrac{d{L}'}{dt}={{{\tau }'}_{ext}}$ where $ {{{\tau }'}_{ext}}$ is the sum of all external torques acting on the system about the centre of mass. (Hint: Use the definition of centre of mass and Newton’s Third Law. Assume the internal forces between any two particles act along the line joining the particles.)

Ans: We have the following relation:

$ {L}'={{\sum\limits_{i}{{{r}_{i}}}}^{\prime }}\times {{p}_{i}}^{\prime }$ 

$ \dfrac{d{L}'}{dt}=\dfrac{d}{dt}\left( \sum\limits_{i}{{{r}_{i}}^{\prime }\times {{p}_{i}}^{\prime }} \right)$ 

$ \Rightarrow \dfrac{d{L}'}{dt}=\dfrac{d}{dt}\left( \sum\limits_{i}{{{r}_{i}}^{\prime }} \right)\times {{p}_{i}}^{\prime }+\sum\limits_{i}{{{r}_{i}}^{\prime }}\times \dfrac{d}{dt}\left( {{p}_{i}}^{\prime } \right)$ 

$ \Rightarrow \dfrac{d{L}'}{dt}=\dfrac{d}{dt}\left( \sum\limits_{i}{{{m}_{i}}{{r}_{i}}^{\prime }} \right)\times {{v}_{i}}^{\prime }+\sum\limits_{i}{{{r}_{i}}^{\prime }}\times \dfrac{d}{dt}\left( {{p}_{i}}^{\prime } \right)$ 

Where,

$ {{r}_{i}}^{\prime }$ is the position vector with respect to the centre of mass of system of particles.

$ \sum\limits_{i}{{{m}_{i}}{{r}_{i}}^{\prime }}=0$ 

$ \dfrac{d{L}'}{dt}=\sum\limits_{i}{{{r}_{i}}^{\prime }}\times \dfrac{d}{dt}\left( {{p}_{i}}^{\prime } \right)$ 

We have the following relation:

$ \Rightarrow \dfrac{d{L}'}{dt}=\sum\limits_{i}{{{r}_{i}}^{\prime }}\times {{m}_{i}}\dfrac{d}{dt}\left( {{v}_{i}}^{\prime } \right)$ 

Where, 

$ \dfrac{d}{dt}\left( {{v}_{i}}^{\prime } \right)$ is the rate of change of velocity of the $ {{i}^{th}}$ particle with respect to the centre of mass of the system.

Therefore, according to Newton’s third law of motion, we can express:

$ {{m}_{i}}\dfrac{d}{dt}\left( {{v}_{i}}^{\prime } \right)$ is the external force acting on the $ {{i}^{th}}$ particle.

$ {{\sum\limits_{i}{\left( {{\tau }_{i}}^{\prime } \right)}}_{ext}}$ i.e., $ \sum\limits_{i}{{{r}_{i}}^{\prime }}\times {{m}_{i}}\dfrac{d}{dt}\left( {{v}_{i}}^{\prime } \right)={{{\tau }'}_{ext}}$ is the external torque acting on the system as a whole.

Hence, $ \dfrac{d{L}'}{dt}={{{\tau }'}_{ext}}$.

Download Important Questions For Class 11 Physics Chapter 6 PDF

Physics Class 11 Chapter 6 Important Questions

Chapter 6 system of particles and rotational motion is one of the important concepts to be learned in Class 11 Physics. The system of particles and rotational motion is one of those chapters where it requires a lot of imagination for understanding the concepts. Before starting with Physics Class 11 Chapter 6 important questions, students must have a great hold on the chapter. By now students must be well versed with concepts like the definition of rotational motion, rigid bodies, centre of mass system, etc. 

Students can boost their preparation with Class 11 Physics Chapter 6 extra questions which will enable them to solve maximum questions and with answers. The system of particles and rotational motion chapter includes various important topics that will enhance the knowledge of rigid body motion with illustrations from the objects we witness to observe in our everyday life. 

Class 11 Physics Rotational Motion Important Questions

Every object we see in our life has a finite structure, we know that rigid bodies are those in which the distance between the particles will remain constant. A rigid body fixed at the point will be only allowed to execute the rotational motion. A free rigid body will be either having a translational motion or both translational and rotational motion.

There are some important topics that will lead to earning good grades in the board exams or in any entrance examinations. Some of the key points of the chapter are as follows:

• Determining the motion of rigid bodies, the centre of mass of the system.

• Finding the density of the body depending upon the type of distribution of particles. The distribution of the particles will be either discrete or continuous systems.

• Introducing the concept of torque. Explanation and effect of torque on the rigid bodies.

• Rotational motion visualization, explaining conservation laws, etc.

Like these, we come across several interesting topics under Chapter 6 of Class 11 Physics. For a detailed understanding of the concepts, students must practice Chapter 6 Physics Class 11 important questions. The only key to master any subject is constant determination and practising every day. The detailed revision notes, chapter-wise materials, important questions, etc. are available on the Vedantu website in the PDF form and students can download them anytime.

Conclusion

Vedantu’s Important Questions for CBSE Class 11 Physics Chapter 6 - "Systems of Particles and Rotational Motion" serves as a crucial asset for students. These questions are strategically designed to cover vital concepts and fundamental principles related to rotational dynamics. They offer students a targeted approach to exam preparation, helping them identify key areas of focus and providing an opportunity for self-assessment. By mirroring the examination pattern and difficulty level, these important questions enable students to build confidence and proficiency in the subject. Overall, they are an invaluable resource that empowers Class 11 Physics students to excel in their studies and perform exceptionally well in their exams.

Important Related Links for CBSE Class 11