Maths Notes for Chapter 14 Probability Class 11 - FREE PDF Download
FAQs on Probability Class 11 Maths Chapter 14 CBSE Notes - 2025-26
1. What are the most important concepts students should focus on while revising Probability for Class 11 Maths as per the CBSE 2025–26 syllabus?
When revising Probability for Class 11 Maths, focus on the following concepts:
- Definitions: random experiments, sample space, outcome, event.
- Types of events: simple, compound, mutually exclusive, exhaustive, complementary.
- Approaches to probability: statistical, classical, and axiomatic.
- Key formulas: P(E) = Number of favourable outcomes / Total number of outcomes, addition and multiplication rules.
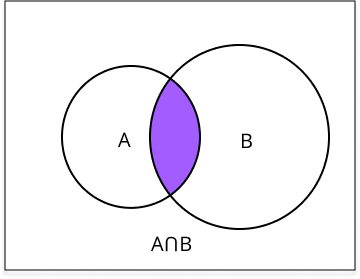
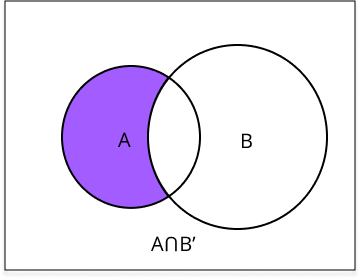
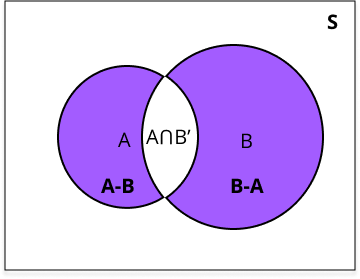
- Algebra of events: union, intersection, complement.
2. How should students structure their quick revision for the Probability chapter to maximise their score in Class 11 Maths?
Organise your quick revision using this sequence:
- Review key terms and their definitions.
- Memorise essential formulas and theorem statements.
- Revisit different event types and their properties.
- Work through core CBSE-style example problems.
- Create a visual summary with concept maps or tables for last-minute recall.
3. What is the key difference between the classical, statistical, and axiomatic approaches of probability as explained in the Class 11 revision notes?
The classical approach applies when all outcomes are equally likely, like tossing a coin. The statistical approach is based on observed frequencies from experiments or data, making it useful for real-world situations. The axiomatic approach generalises probability using set theory and three main axioms, allowing application to both simple and complex cases. Understanding these helps students select the right method for any CBSE probability problem.
4. Which topics and concepts should have the highest priority during last-minute revision of Probability in Class 11 Maths?
Prioritise these during last-minute revision:
- Main definitions and event types (mutually exclusive, exhaustive, complementary).
- Core probability formulas and rules (addition, multiplication, complement).
- Common CBSE exam patterns and HOTS questions based on real-life application and calculation.
- Summary tables and concept charts for visual memory.
5. How can the concept of complementary events be used to speed up problem-solving during revision and exams?
Complementary events often make it faster to solve probability questions. Instead of calculating P(A) directly, sometimes it's simpler to find P(not A), and then use P(A) = 1 − P(not A). This approach is especially helpful when the complement has fewer outcomes or is easier to enumerate, saving time and reducing errors in exam situations.
6. Why do all probability values fall between 0 and 1 according to the CBSE Class 11 syllabus?
Probability indicates the likelihood of an event. A value of 0 means the event is impossible; a value of 1 means the event is certain. By definition, all probabilities must satisfy 0 ≤ P(E) ≤ 1, as per the axiomatic approach in the CBSE syllabus. This ensures consistency and logical correctness in all probability calculations.
7. What are some common misconceptions students should avoid while revising Probability for board exams?
Avoid these misconceptions:
- Assuming outcomes are always equally likely without checking conditions.
- Confusing mutually exclusive with independent events.
- Overlooking overlap in compound events when applying the addition rule.
- Failing to list all possible outcomes before calculating probability.
8. How are mutually exclusive and exhaustive events different, and why does this matter in Class 11 Probability revision?
Mutually exclusive events cannot happen at the same time (their intersection is empty), while exhaustive events together cover all possible outcomes of the experiment (their union equals the sample space). Understanding this distinction is essential because many probability rules, such as addition and subtraction, depend on the event types in a question.
9. What strategies can help students tackle calculation-heavy or tricky probability questions in exams?
Use these strategies:
- Systematically list the sample space to avoid missed outcomes.
- Identify favourable outcomes precisely.
- Apply the complement rule when direct calculation is complex.
- Break compound events into simpler events for clarity.
- Double-check for overlapping cases before using addition or subtraction formulas.
10. How does understanding the algebra of events help improve revision and performance in Probability?
Algebra of events involves combining events through union, intersection, and complement. Mastering this lets students approach varied probability questions methodically, especially those that present unfamiliar or compound situations. This makes revision more effective and deepens conceptual clarity, as required by the CBSE curriculum.
11. What is the most efficient order to revise the Probability chapter for the Class 11 board exam?
Follow this order for efficient revision:
- Start with essential definitions (experiment, outcome, event, sample space).
- Review event types and their distinguishing features.
- Study the three approaches to probability and related formulas.
- Practice mixed examples, moving from basic to advanced.
- Recap everything using a concept map or summary chart for quick recall.
12. How do the three approaches to probability relate to real-world examples in the Class 11 curriculum?
The statistical approach uses real-life data, like survey results or frequency of events. The classical approach is applied to theoretical experiments (e.g., cards, dice) with equally likely outcomes. The axiomatic approach is useful for proving general results or solving problems where specific outcomes are complex. Recognising which approach to use is critical for both understanding and accurately answering CBSE exam questions.
13. In what ways does set theory help in understanding and applying probability concepts in Class 11 revision notes?
Set theory provides the language for describing events and sample spaces in probability. Operations like union (for ‘or’ events), intersection (for ‘and’ events), and complement (for ‘not’ events) correspond directly to probability rules, making problem-solving clearer and less error-prone in board-level questions.
14. How can concept maps and summary tables help students during last-minute revision of Probability?
Concept maps and summary tables allow students to see relationships between event types, rules, and formulas at a glance. This helps with quick recall, efficient self-checking, and ensures major topics are covered—boosting confidence before the exam.
15. Which types of practice problems ensure balanced revision of theory and problem-solving in Probability for Class 11 Maths?
Balance your revision by practising:
- Theoretical problems on event definitions and identifying approaches.
- Calculation-based questions involving equally likely outcomes.
- Problems that apply addition, multiplication, and complement rules.
- Higher Order Thinking Skills (HOTS) questions similar to those in CBSE pattern.