Class 11 Maths Chapter 2 Summary Notes PDF Download
FAQs on CBSE Notes Class 11 Maths Chapter 2 - Relations and Functions - 2025-26
1. What core topics should be prioritised for quick revision in Class 11 Maths Chapter 2: Relations and Functions?
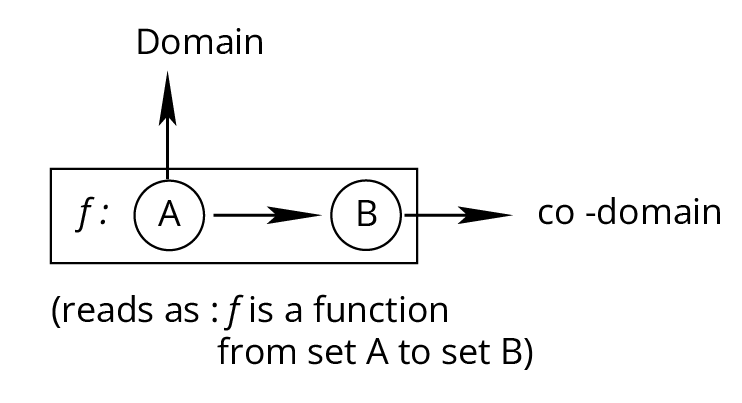
Focus first on foundational definitions such as relation, function, domain, range, and co-domain. Then review types of functions (one-one, onto, bijective, identity, constant, modulus, signum, greatest integer, exponential, logarithmic functions) and the properties of relations (reflexive, symmetric, transitive, equivalence). Finish with the algebra of real functions and basic graph interpretations, ensuring all examples and solved problems are understood.
2. How should students structure their revision for Relations and Functions to optimise exam performance?
Begin revision with definitions and properties of relations and functions. Next, focus on computing domain and range for various functions. Move on to types of functions and key formulas. End by practising algebra of functions (addition, subtraction, multiplication, division) and reviewing solved examples for typical problems seen in CBSE exams. This sequential flow helps build conceptual clarity efficiently.
3. Why is understanding the difference between domain and range essential during revision?
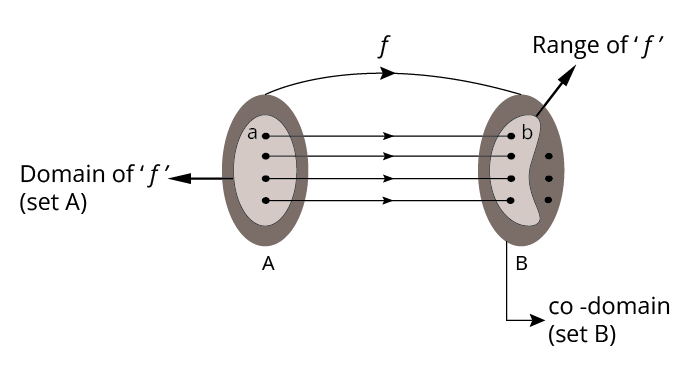
The domain is the set of all valid input values for a function, while the range is the set of possible output values. Knowing how to correctly find each is vital because most exam questions require determining where a function is defined and what outputs can result, ensuring you avoid invalid steps in problem-solving and strengthen answer accuracy.
4. What strategies help in memorising critical formulas for Relations and Functions during fast revision?
Use concept maps to visually link key formulas and definitions. Practice each formula with a solved example to reinforce understanding. Create flashcards for identities such as inverses and types of function mappings. Self-testing and recall drills are also highly effective for long-term retention.
5. What is the best way to distinguish one-one, onto, and bijective functions in revision notes?
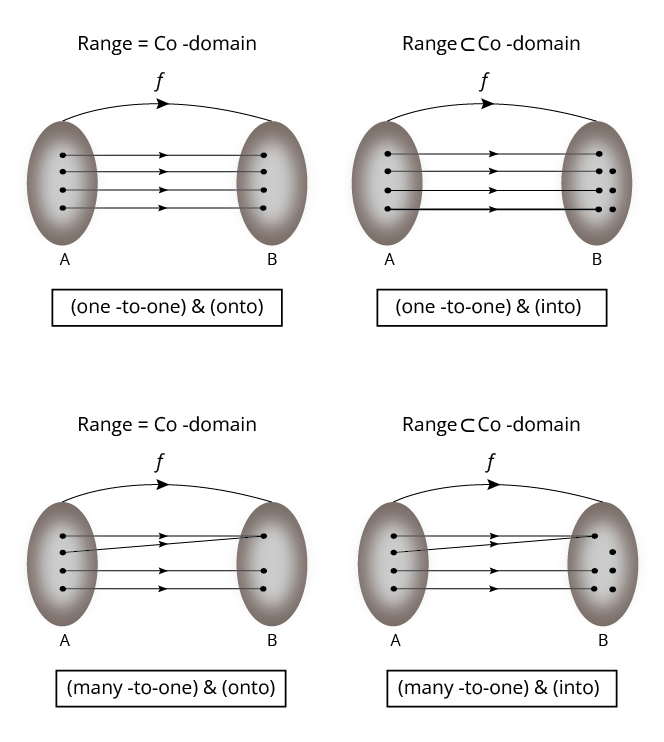
Remember that a one-one (injective) function maps each input to a unique output, onto (surjective) ensures all outputs in the co-domain are achieved, and bijective satisfies both conditions. Use mapping diagrams or solved example sets to practise quick identification, as often required in conceptual exam questions.
6. How does understanding the algebra of real functions support overall mastery in this chapter?
Mastery of algebra of real functions—adding, subtracting, multiplying, dividing, and scalar multiplication—helps in solving composite problems, graph transformations, and linking concepts across questions. This is frequently tested through questions involving operations between two or more given functions and requires understanding interval domains where the operations are valid.
7. Which types of functions should students memorise the graphs and properties of for effective exam revision?
Make sure to memorise standard graphs and properties of these functions: identity, constant, modulus, signum, greatest integer, exponential, and logarithmic. Understanding their domains, ranges, and graphical behaviour enables rapid response to related questions and assists in quickly analysing function transformations under algebraic operations.
8. How can concept maps improve preparation for Relations and Functions revision?
Concept maps visually organise the hierarchy and connections between definitions, properties, examples, and formulas. This helps quickly recall details, see links between seemingly different concepts, and strengthens structural memory—especially useful for theory-based or comprehensive revision questions.
9. What are some common misconceptions students should watch out for when revising relations versus functions?
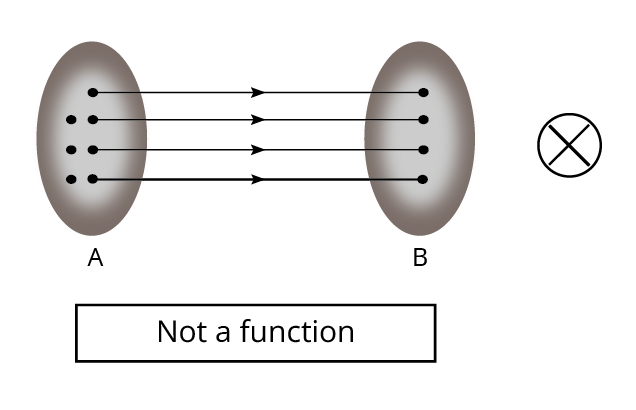
A common misconception is treating any relation as a function. A function requires every input to be associated with exactly one output, while a relation does not. Regularly practise identifying sets that fail or satisfy this property, as exam questions often test this distinction.
10. How should students work through solved examples in revision notes to handle new and unfamiliar questions in exams?
Study solved examples not just for the answer, but to understand each step and the reasoning involved in selecting formulas or theorems. Try to solve the examples independently first, then cross-check with the solution. This builds confidence to approach unfamiliar questions and establishes patterns for applying concepts under exam pressure.
11. In what way does using well-structured revision notes for Relations and Functions benefit exam preparation over re-reading the full textbook?
Well-structured revision notes condense fundamental concepts, definitions, key formulas, and solved examples into a focused format, facilitating faster recall and efficient practice. This targeted approach saves time, ensures comprehensive coverage, and supports effective last-minute revision, compared to the more time-consuming and broader reading of textbooks.
12. How can students clarify confusion between even, odd, and periodic functions during revision?
Use the following checks in your notes:
- Even function: f(-x) = f(x); graph is symmetric about the y-axis
- Odd function: f(-x) = -f(x); graph is symmetric about the origin
- Periodic function: f(x+T) = f(x) for some period T; graph repeats at interval T
13. How does knowledge of Relations and Functions apply to other chapters in Class 11 Maths?
Understanding core ideas from Relations and Functions, such as function properties and compositions, is essential for topics in calculus, sets, and trigonometry. Recognising these links aids in building a holistic understanding and helps solve integrated problems found in advanced chapters.
14. What is the significance of inverse functions during last-minute revision for this chapter?
Inverse functions allow the reversal of an original function’s mapping, so outputs become inputs. Only bijective functions have inverses. It's crucial to practise switching variables and verifying that composing a function with its inverse returns the starting value, as this is a popular question type in CBSE exams.
15. How should students approach revision for topics removed or updated in the recent CBSE 2025–26 syllabus changes for Relations and Functions?
Refer only to the latest CBSE syllabus and exclude topics marked as deleted (such as certain composite function details). Focus on the official list of prescribed concepts and types, using up-to-date summary tables and practising only relevant question types for optimal exam alignment.