Maths Notes for Chapter 3 Trigonometric Functions Class 11 - FREE PDF Download
FAQs on CBSE Notes Class 11 Maths Chapter 3 - Trigonometric Functions - 2025-26
1. What are the key concepts summarised in the Class 11 trigonometric functions revision notes?
The Class 11 trigonometric functions revision notes focus on trigonometric identities, formulae for angle sum and difference, double and triple angle formulas, functions’ domains and ranges, and methods to solve trigonometric equations. They also summarise the key relationships between trigonometric ratios and cover principal and general solutions, as per the CBSE 2025–26 syllabus.
2. How can students use these revision notes for quick and effective exam revision?
Students can use the revision notes by reviewing summarised formulas and identities, studying the concept map for interconnections between topics, and practising the example problems provided. The notes are designed to help with last-minute revision by consolidating complex concepts into easy-to-remember points, ensuring coverage of all key areas before exams.
3. What is the best revision order for trigonometric functions in Class 11 to maximise understanding?
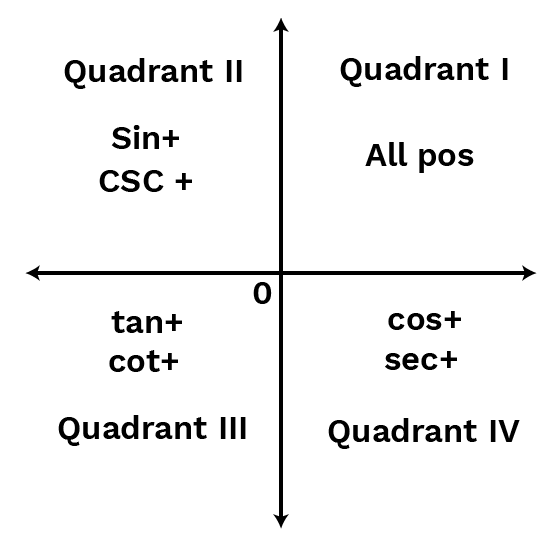
For efficient revision, start with basic trigonometric ratios and their signs in different quadrants, then move to key identities and formulas, followed by angle transformations (sums, differences, multiples). Next, revise solving trigonometric equations and finally practice applied problems connecting different topics for comprehensive understanding.
4. Why is it important to master trigonometric identities and formulas during revision?
Mastering trigonometric identities and formulas is crucial because they form the foundation for solving a wide range of problems in both school exams and competitive tests. Proficiency in these allows students to quickly recognise patterns, choose the right method, and avoid common calculation errors, greatly improving problem-solving speed and accuracy in assessments.
5. How do concept maps help in revising trigonometric functions for Class 11 exams?
Concept maps visually organise the relationships between identities, formulas, and problem types, making it easier to recall connections during exams. Using a concept map during revision can help students review all key ideas at a glance, identify knowledge gaps, and strengthen their ability to link concepts quickly in unfamiliar questions.
6. What types of problems should be prioritised during last-minute revision for trigonometric functions?
During last-minute revision, prioritise formula-based questions, identity verifications, and standard value calculations. Also, focus on solving different types of trigonometric equations and practical applications such as finding the lengths or angles in geometric problems, all aligned with the CBSE Class 11 syllabus.
7. How are domains and ranges of trigonometric functions vital for solving textbook and board problems?
Understanding the domains and ranges of trigonometric functions helps students avoid invalid solutions and correctly identify the principal and general solutions for equations. This knowledge is tested frequently in exams through questions that ask for possible values of variables or constraints on angle measures.
8. What are some common misconceptions students have about trigonometric functions during revision, and how can notes help address them?
Common misconceptions include incorrect quadrant sign assignment, misusing identities, and confusing the domains of different functions. Well-structured revision notes address these by offering stepwise explanations, highlighting exceptions, and providing comparison tables of values and identities to reinforce correct usage.
9. How does revising with formula sheets and value tables benefit trigonometry preparation?
Revising with formula sheets and trigonometric value tables enables students to quickly recall standard results during exams, saving valuable time. These tools also support error-checking and reinforce memory, which is essential for solving multi-step problems efficiently.
10. Which key trigonometric formulas are most essential to memorise for Class 11 exams and why?
Students must memorise:
- Basic identities: (e.g., sin2θ + cos2θ = 1)
- Angle sum & difference formulas
- Double and triple angle formulas
- Product-to-sum and sum-to-product identities
- Standard function values at common angles