Question

What is a position vector?

Answer 1

Hint: One end of the position vector is always fixed and the other end of the position vector kept on moving either on clockwise or in anti-clockwise so use this concept to reach the solution of the question.

Complete step-by-step solution -

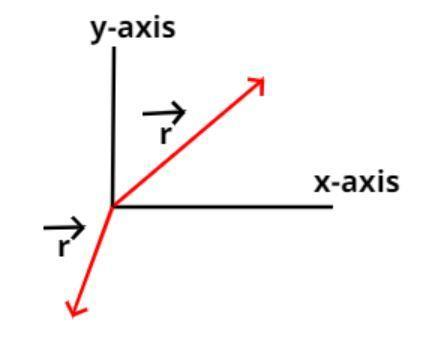
Position vector, straight line having one end fixed to a body and the other end attached to a moving point and used to describe the position of the point relative to the body. As the point moves, the position vector will change in length or in direction or in both length and direction, as shown in the figure.
Here we show the position vector (r) in two dimensional space (i.e. in x and y-axis).
The coordinates of r is
$\left( {r\cos \theta ,r\sin \theta } \right)$ general polar coordinates of position vector (r) where $\theta $ is taken from the positive direction of the x-axis moving anti-clockwise.
So the position vector r is written as,
$ \Rightarrow \vec r = r\cos \theta \hat i + r\sin \theta \hat j$, where $\hat i,\hat j$ are the direction of x and y axis respectively.
So as we see that the position vector has magnitude as well as direction so position vector is a vector quantity not a scalar quantity as in scalar quantity there is only magnitude.
For different points the position vector is different so as the magnitude as well as the direction as shown in the figure.
In three dimensional the position vector $\left( {\vec r} \right)$ is given as
$ \Rightarrow \vec r = x\hat i + y\hat j + z\hat k$
Where, $\hat i$ = unit vector along x direction, $\hat j$ = unit vector along y direction and $\hat k$ = unit vector along z direction.
So, this is the required answer.

Note – Whenever we face such types of questions the key concept is position vector is nothing but a moving point w.r.t. the fixed point or the body either in clockwise or in anti-clockwise position vector can be 2-D or 3-D.