
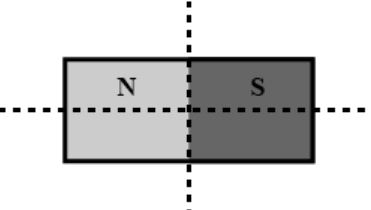
Time period for a magnet is T. If it is divided in four equal parts along its axis and perpendicular to its axis as shown then time period for each part will be
A. $4T$
B. $\dfrac{T}{4} \\ $
C. $\dfrac{T}{2} \\ $
D. $T$
Answer
233.1k+ views
Hint: The length bar magnet must be divided into four equal parts, each of which must have the same length and width. The bar magnet can only be divided into four equal parts by first cutting it parallel to its length and then perpendicular to it, so that each piece is half as long as it originally was and half as wide.
Formula used:
The expression of time period of a magnet is,
$T = 2\pi \sqrt {\dfrac{I}{{MB}}} $
Here, $M$ is the magnetic moment, $B$ is the magnetic field and $I$ is the moment of inertia.
Complete step by step solution:
The term "bar magnet" refers to a magnetic bar. The poles are the ends of the bar magnet. A dipole is the bar magnet. Pole strength is the name of the physical property that describes the magnetization of the poles.
The magnet has been divided into four equal pieces by cutting it equally along its length and width, as shown in the diagram. To accomplish this, one must cut the magnets parallel to their length such that the length stays the same and the breadth is cut in half. The length must now also be cut in half because the magnet must once more be cut perpendicular to the length. The four pieces will therefore be equal. Time period of original magnet is given by
$T = 2\pi \sqrt {\dfrac{I}{{MB}}} $
Where $I$ is the inertia which is equal to $\dfrac{{m{L^2}}}{{12}}$ and $M = qL$
Since it is cut into 4 pieces the inertia will change. The new inertia is
${I^1} = \dfrac{{\dfrac{m}{4}{{(\dfrac{L}{2})}^2}}}{{12}} \\
\Rightarrow {I^1} = \dfrac{{m{L^2}}}{{16 \times 12}} \\
\Rightarrow {I^1} = \dfrac{I}{{16}}$
New dipole will be $ = \dfrac{q}{2} \times \dfrac{L}{2} = \dfrac{M}{4}$
So we can say that new time period
${T^1} = 2\pi \sqrt {\dfrac{{\dfrac{I}{{16}}}}{{\dfrac{{MB}}{4}}}} \\$
$\Rightarrow {T^1} = \dfrac{1}{2} \times 2\pi \sqrt {\dfrac{I}{{MB}}} \\ $
$\therefore {T^1} = \dfrac{T}{2}$
Hence option C is correct.
Note: The pole strengths alter depending on the length and area of the magnet after it has been cut, but the north and south poles stay the same. Each slice of the magnet is four times weaker than the original magnet due to reductions in the magnetization and magnetic moments.
Formula used:
The expression of time period of a magnet is,
$T = 2\pi \sqrt {\dfrac{I}{{MB}}} $
Here, $M$ is the magnetic moment, $B$ is the magnetic field and $I$ is the moment of inertia.
Complete step by step solution:
The term "bar magnet" refers to a magnetic bar. The poles are the ends of the bar magnet. A dipole is the bar magnet. Pole strength is the name of the physical property that describes the magnetization of the poles.
The magnet has been divided into four equal pieces by cutting it equally along its length and width, as shown in the diagram. To accomplish this, one must cut the magnets parallel to their length such that the length stays the same and the breadth is cut in half. The length must now also be cut in half because the magnet must once more be cut perpendicular to the length. The four pieces will therefore be equal. Time period of original magnet is given by
$T = 2\pi \sqrt {\dfrac{I}{{MB}}} $
Where $I$ is the inertia which is equal to $\dfrac{{m{L^2}}}{{12}}$ and $M = qL$
Since it is cut into 4 pieces the inertia will change. The new inertia is
${I^1} = \dfrac{{\dfrac{m}{4}{{(\dfrac{L}{2})}^2}}}{{12}} \\
\Rightarrow {I^1} = \dfrac{{m{L^2}}}{{16 \times 12}} \\
\Rightarrow {I^1} = \dfrac{I}{{16}}$
New dipole will be $ = \dfrac{q}{2} \times \dfrac{L}{2} = \dfrac{M}{4}$
So we can say that new time period
${T^1} = 2\pi \sqrt {\dfrac{{\dfrac{I}{{16}}}}{{\dfrac{{MB}}{4}}}} \\$
$\Rightarrow {T^1} = \dfrac{1}{2} \times 2\pi \sqrt {\dfrac{I}{{MB}}} \\ $
$\therefore {T^1} = \dfrac{T}{2}$
Hence option C is correct.
Note: The pole strengths alter depending on the length and area of the magnet after it has been cut, but the north and south poles stay the same. Each slice of the magnet is four times weaker than the original magnet due to reductions in the magnetization and magnetic moments.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding the Electric Field of a Uniformly Charged Ring

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance




