Question

The maximum value of \[Z{\text{ = }}4x + 2y\] subject to constraints \[2x + 3y \leqslant 18\] , \[x + y \geqslant 10\] and \[x,y \geqslant 0\] is
(A) \[20\]
(B) \[36\]
(C) \[40\]
(D) None of these

Answer 1

Hint: On converting the given inequalities into equations we get the points to be plotted on the graph. From the graph, we can obtain a feasible point by determining a common point that satisfies all the inequalities simultaneously.

Complete step by step Solution:
Given,
\[Z = 4x + 2y\] subject to constraints \[2x + 3y \leqslant 18\] and \[x + y \geqslant 10\] where \[x \geqslant 0\] and \[y \geqslant 0\]
Let us consider the inequalities as equalities for some time,
\[2x + 3y = 18\] … \[(1)\]
\[x + y = 10\]… \[(2)\]
From \[(1)\] we get \[x = 0 \Rightarrow y = 6\] and \[y = 0 \Rightarrow x = 9\]
So, the points (0,6) and (9,0) lie on the line given in \[(1)\].
From \[(2)\] we get \[x = 0 \Rightarrow y = 10\] and \[y = 0 \Rightarrow x = 10\]
So, the points (0,10) and (10,0) lie on the line given in \[(2)\].
On plotting these points considering the inequalities, we get the graph in which the shaded part shows the feasible region.

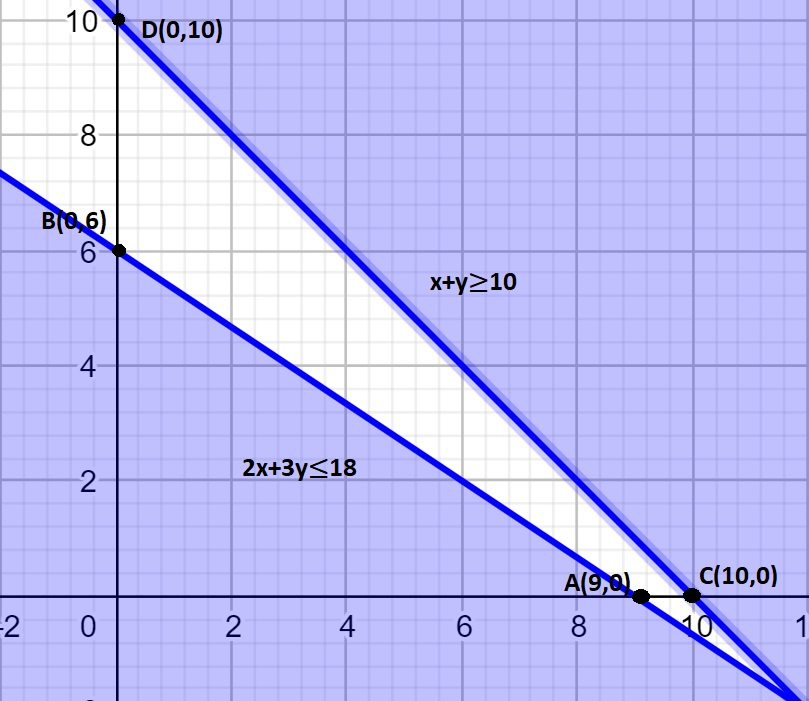
We can clearly see that there is no area in the 1st quadrant where the two inequalities meet.
Hence there is no solution for the LPP with the given constraints and Z cannot be maximized
Hence, the correct option is (D).

Note: The solutions of the LPP are obtained from the point where the inequalities meet. If there is no point in satisfying all the inequations simultaneously then there is no feasible point and the solution is said to be infeasible.