
The function arctan(sinx + cosx) is increasing in the interval
[a] $\left( \dfrac{\pi }{4},\dfrac{\pi }{2} \right)$
[b] $\left( -\dfrac{\pi }{2},\dfrac{\pi }{4} \right)$
[c] $\left( 0,\dfrac{\pi }{2} \right)$
[d] $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$
Answer
232.8k+ views
Hint: Use the fact that if f(x) is an increasing function, then $f'\left( x \right)\ge 0$. Alternatively, use the fact that if f(x) is an increasing function, then $fog\left( x \right)$ is an increasing function whenever g(x) is increasing and $fog\left( x \right)$ is a decreasing function whenever g(x) is a decreasing function.
Complete step-by-step solution -
We have f(x) = arctan(sinx+cosx)
Differentiating both sides, we get
$f'\left( x \right)=\dfrac{d}{dx}\left( \arctan \left( \sin x+\cos x \right) \right)$
We know from chain rule of differentiation that $\dfrac{d}{dx}\left( f\left( g\left( x \right) \right) \right)=\dfrac{d}{d\left( g\left( x \right) \right)}f\left( g\left( x \right) \right)\dfrac{d}{dx}\left( g\left( x \right) \right)$
Hence $f'\left( x \right)=\dfrac{d}{d\left( \sin x+\cos x \right)}\arctan \left( \sin x+\cos x \right)\dfrac{d}{dx}\left( \sin x+\cos x \right)$
We know that $\dfrac{d}{dx}\arctan x=\dfrac{1}{1+{{x}^{2}}}$
Hence we have
$f'\left( x \right)=\dfrac{1}{{{\left( \sin x+\cos x \right)}^{2}}+1}\dfrac{d}{dx}\left( \sin x+\cos x \right)$
We know that $\dfrac{d}{dx}\left( f\left( x \right)+g\left( x \right) \right)=\dfrac{d}{dx}\left( f\left( x \right) \right)+\dfrac{d}{dx}\left( g\left( x \right) \right)$
Using , we get
$f'\left( x \right)=\dfrac{1}{1+{{\left( \sin x+\cos x \right)}^{2}}}\left( \dfrac{d}{dx}\sin x+\dfrac{d}{dx}\cos x \right)$
Since $\dfrac{d}{dx}\sin x=\cos x$ and $\dfrac{d}{dx}\cos x=-\sin x$, we have
$f'\left( x \right)=\dfrac{1}{1+{{\left( \sin x+\cos x \right)}^{2}}}\left( \cos x-\sin x \right)$
Now for f(x) to be increasing, we have
$f'\left( x \right)\ge 0$
Hence, we have
$\dfrac{1}{1+{{\left( \sin x+\cos x \right)}^{2}}}\left( \cos x-\sin x \right)\ge 0$
Since $\dfrac{1}{1+{{\left( \sin x+\cos x \right)}^{2}}}>0$ , we have
$\left( \cos x-\sin x \right)\ge 0$
Hence $\cos x>\sin x$
In the interval $\left( -\dfrac{\pi }{2},\dfrac{\pi }{4} \right)$ cosx>sinx.
Hence we have
In the interval $\left( -\dfrac{\pi }{2},\dfrac{\pi }{4} \right)$ f(x) is increasing.
Hence option [b] is correct.
Note: Alternatively, we have,
arc tanx is an increasing function. Hence arctan(cosx+sinx) is increasing whenever sinx+cosx is increasing.
Now sinx +cosx $=\dfrac{1}{\sqrt{2}}\left( \sin \left( x-\dfrac{\pi }{4} \right) \right)$
Now we know that sinx is an increasing function in the interval $\left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$
Hence $\sin x+\cos x$ is increasing in the interval $\left( \dfrac{-\pi }{2}-\dfrac{\pi }{4},\dfrac{\pi }{2}-\dfrac{\pi }{4} \right)=\left( \dfrac{-3\pi }{4},\dfrac{\pi }{4} \right)$
Hence sinx + cosx is increasing in the interval $\left( \dfrac{-\pi }{2},\dfrac{\pi }{4} \right)$
Hence option [b] is correct.
Graph of arctan(sinx+cosx)
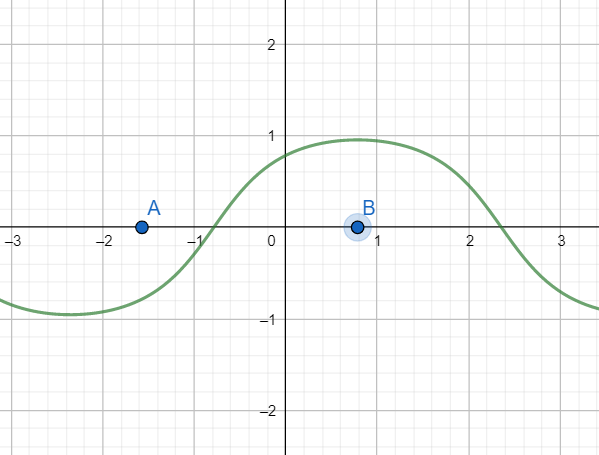
As is evident from the graph that f(x) is increasing in interval [A,B], where $\text{A=}\dfrac{-\pi }{2}$ and $\text{B=}\dfrac{\pi }{4}$.
Complete step-by-step solution -
We have f(x) = arctan(sinx+cosx)
Differentiating both sides, we get
$f'\left( x \right)=\dfrac{d}{dx}\left( \arctan \left( \sin x+\cos x \right) \right)$
We know from chain rule of differentiation that $\dfrac{d}{dx}\left( f\left( g\left( x \right) \right) \right)=\dfrac{d}{d\left( g\left( x \right) \right)}f\left( g\left( x \right) \right)\dfrac{d}{dx}\left( g\left( x \right) \right)$
Hence $f'\left( x \right)=\dfrac{d}{d\left( \sin x+\cos x \right)}\arctan \left( \sin x+\cos x \right)\dfrac{d}{dx}\left( \sin x+\cos x \right)$
We know that $\dfrac{d}{dx}\arctan x=\dfrac{1}{1+{{x}^{2}}}$
Hence we have
$f'\left( x \right)=\dfrac{1}{{{\left( \sin x+\cos x \right)}^{2}}+1}\dfrac{d}{dx}\left( \sin x+\cos x \right)$
We know that $\dfrac{d}{dx}\left( f\left( x \right)+g\left( x \right) \right)=\dfrac{d}{dx}\left( f\left( x \right) \right)+\dfrac{d}{dx}\left( g\left( x \right) \right)$
Using , we get
$f'\left( x \right)=\dfrac{1}{1+{{\left( \sin x+\cos x \right)}^{2}}}\left( \dfrac{d}{dx}\sin x+\dfrac{d}{dx}\cos x \right)$
Since $\dfrac{d}{dx}\sin x=\cos x$ and $\dfrac{d}{dx}\cos x=-\sin x$, we have
$f'\left( x \right)=\dfrac{1}{1+{{\left( \sin x+\cos x \right)}^{2}}}\left( \cos x-\sin x \right)$
Now for f(x) to be increasing, we have
$f'\left( x \right)\ge 0$
Hence, we have
$\dfrac{1}{1+{{\left( \sin x+\cos x \right)}^{2}}}\left( \cos x-\sin x \right)\ge 0$
Since $\dfrac{1}{1+{{\left( \sin x+\cos x \right)}^{2}}}>0$ , we have
$\left( \cos x-\sin x \right)\ge 0$
Hence $\cos x>\sin x$
In the interval $\left( -\dfrac{\pi }{2},\dfrac{\pi }{4} \right)$ cosx>sinx.
Hence we have
In the interval $\left( -\dfrac{\pi }{2},\dfrac{\pi }{4} \right)$ f(x) is increasing.
Hence option [b] is correct.
Note: Alternatively, we have,
arc tanx is an increasing function. Hence arctan(cosx+sinx) is increasing whenever sinx+cosx is increasing.
Now sinx +cosx $=\dfrac{1}{\sqrt{2}}\left( \sin \left( x-\dfrac{\pi }{4} \right) \right)$
Now we know that sinx is an increasing function in the interval $\left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$
Hence $\sin x+\cos x$ is increasing in the interval $\left( \dfrac{-\pi }{2}-\dfrac{\pi }{4},\dfrac{\pi }{2}-\dfrac{\pi }{4} \right)=\left( \dfrac{-3\pi }{4},\dfrac{\pi }{4} \right)$
Hence sinx + cosx is increasing in the interval $\left( \dfrac{-\pi }{2},\dfrac{\pi }{4} \right)$
Hence option [b] is correct.
Graph of arctan(sinx+cosx)

As is evident from the graph that f(x) is increasing in interval [A,B], where $\text{A=}\dfrac{-\pi }{2}$ and $\text{B=}\dfrac{\pi }{4}$.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding the Electric Field of a Uniformly Charged Ring

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance

Understanding How a Current Loop Acts as a Magnetic Dipole

Understanding Average and RMS Value in Electrical Circuits




