Question

The area bounded by the parabola (${y^2} = 4ax$), latus rectum and x-axis.
$\left( a \right)0$
$\left( b \right)\dfrac{4}{3}{a^2}$
$\left( c \right)\dfrac{8}{3}{a^2}$
$\left( d \right)\dfrac{{{a^2}}}{3}$

Answer 1

Hint: In this particular question first draw the pictorial representation of all the given curves and highlight the area and mark all the intersection points it will give us a clear idea of what we have to calculate then apply the concept of symmetry then apply the integration formula to calculate the area bounded by the curves.

Complete step-by-step answer:

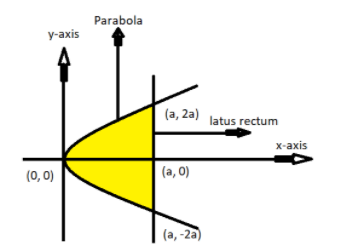
Given equation of parabola is ${y^2} = 4ax$
As we know this is the standard equation of parabola opening horizontally in the positive side of the x-axis and passing from origin as shown in the above figure.
Now as we know that the coordinates of the focus of this parabola is lying on the x-axis having coordinates (a, 0).
And the latus rectum of the parabola is passing from the focus having length 4a, i.e. 2a upwards and 2a downwards.
So the intersection point of the latus rectum and the parabola is (a, 2a) and (a, -2a) as shown in the above figure.
Now the area bounded by the curves is highlighted by the yellow color.
As we see that the upward area is similar to the downward area so the area bounded by the curves is twice the upward area.
Now the area bounded by the curve is given as $A = \int_{{x_1}}^{{x_2}} {\left( {{y_1} - {y_2}} \right)dx} $ now for the upward area ${y_1}$ is the upper graph of parabola (i.e. positive part of parabola) so, ${y_1} = \sqrt {4ax} $ and ${y_2}$ is the lower part of the area i.e. x-axis, so ${y_2} = 0$ (as on x-axis y = 0).
And the integration limit is from, x = 0 to x = a.
$ \Rightarrow A = \int_{x = 0}^{x = a} {\left( {\sqrt {4ax} - 0} \right)dx} $
So the total area bounded by the curves is twice of this area.
\[ \Rightarrow {A_{Total}} = 2\int_{x = 0}^{x = a} {\left( {\sqrt {4ax} - 0} \right)dx} \]
Now first simplify we have,
\[ \Rightarrow {A_{Total}} = 2\sqrt {4a} \int_{x = 0}^{x = a} {\left( {{x^{\dfrac{1}{2}}}} \right)dx} \]
Now as we know that $\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C} $, where C is some arbitrary integration constant, so use these properties in the above integral we have,
\[ \Rightarrow {A_{Total}} = 2\sqrt {4a} \left( {\dfrac{{{x^{\dfrac{1}{2} + 1}}}}{{\dfrac{1}{2} + 1}}} \right)_0^a\]
Now apply integration limits we have,
\[ \Rightarrow {A_{Total}} = 2\sqrt {4a} \left( {\dfrac{{{a^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}} - 0} \right)\]
\[ \Rightarrow {A_{Total}} = \dfrac{4}{3}\sqrt {4a} \left( {a\sqrt a } \right) = \dfrac{8}{3}{a^2}\] Sq. units.
So this is the required area.
Hence option (C) is the correct answer.

Note:Whenever we face such types of questions the key concept is the integration formula to calculate the area bounded by the curves which is given as, $A = \int_{{x_1}}^{{x_2}} {\left( {{y_1} - {y_2}} \right)dx} $, where ${y_1}$ is the upper curve and ${y_2}$ is the lower curve and ${x_1}{\text{ and }}{x_2}$ are the lower and upper limits, and always recall the basic integration formula i.e. $\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C} $, where C is some arbitrary integration constant.