
Reading of the voltmeter is ${V_1} = 40V$, ${V_2} = 40V$ and ${V_3} = 10V$. Find:
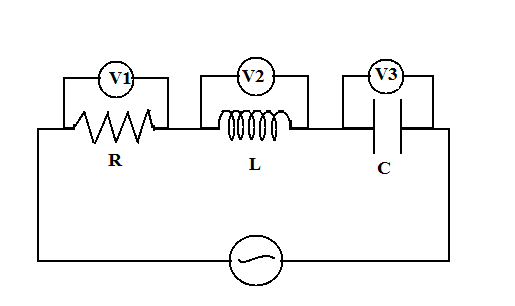
1. ${i_0}, {i_{rms}}, i(t)$
2. ${\varepsilon _0}$
3. $L$ and $C$
Answer
233.1k+ views
Hint: All three are in series and the current in series is the same. This means the value of current should be the same through all the three elements. However the voltage across the capacitor lags from the voltage across the resistor and the voltage across the resistor lags from voltage across the inductor.
Complete step by step solution:
Although the speed of gaseous particles is continuously changing, the velocity distribution does not change. It is difficult to calculate the speed of each single particle, but often we reason for the average behaviour of the particles. Particles that travel in comparison have opposite sign speeds. Since a gas' particles are in random motion, it is plausible that there will be about as many moving in one direction as in the opposite direction, meaning that the average velocity for a collection of gas particles equals zero; as this value is unhelpful, the average of velocities can be determined using an alternative method.
${i_ {rms}} = \dfrac{{{V_1}}}{R}$
Where, ${i_ {rms}} $ is root mean square velocity
$ \Rightarrow {i_ {rms}} = \dfrac{{40}}{4} = 10A$
Formula for ${i_0} $ which is the current produced by the voltage source.
${i_0} = \sqrt 2 {i_ {rms}} $
$ \Rightarrow {i_0} = 10\sqrt 2 A$
${\varepsilon _0} $ is the voltage.
${\varepsilon _0} = \dfrac{{{E_0}}}{{\sqrt 2}}\sqrt {{V^2} _1 + {{({V_2} - {V_1})} ^2}} $
$ \Rightarrow {\varepsilon _0} = \dfrac{{{E_0}}}{{\sqrt 2}}\sqrt {{{40} ^2} + {{(40 - 10)} ^2}} $
$ \Rightarrow {\varepsilon _0} = 50V$
Now,
${X_L} = (\omega L) = \dfrac{{{V_2}}}{{{i_{rms}}}}$
Where, ${X_L} $ is Inductive Reactance
$ \Rightarrow {X_L} = 4\Omega $
$L = \dfrac{4}{\omega} = \dfrac{4}{{100\pi}}H $
$ \Rightarrow L = \dfrac{1}{{25\pi}}$
Where, ${X_C} $ is Capacitive Reactance
${X_C} = \omega C = \dfrac{{{V_1}}}{{{i_{rms}}}}$
$ \Rightarrow {X_C} = 1\Omega $
$ \Rightarrow C = \dfrac{1}{\omega} = \dfrac{1}{{100\pi}}F $
Note: By squaring speeds and taking the square root, we conquer the 'directional' component of speed and at the same time achieve the average speed of the particles. As the value lacks the trajectory of the particles, the average speed is now referred to as the value. Root-medium-square velocity is the calculation of particle speed in a gas described by the square root of the average molecular velocity square of a gas.
Complete step by step solution:
Although the speed of gaseous particles is continuously changing, the velocity distribution does not change. It is difficult to calculate the speed of each single particle, but often we reason for the average behaviour of the particles. Particles that travel in comparison have opposite sign speeds. Since a gas' particles are in random motion, it is plausible that there will be about as many moving in one direction as in the opposite direction, meaning that the average velocity for a collection of gas particles equals zero; as this value is unhelpful, the average of velocities can be determined using an alternative method.
${i_ {rms}} = \dfrac{{{V_1}}}{R}$
Where, ${i_ {rms}} $ is root mean square velocity
$ \Rightarrow {i_ {rms}} = \dfrac{{40}}{4} = 10A$
Formula for ${i_0} $ which is the current produced by the voltage source.
${i_0} = \sqrt 2 {i_ {rms}} $
$ \Rightarrow {i_0} = 10\sqrt 2 A$
${\varepsilon _0} $ is the voltage.
${\varepsilon _0} = \dfrac{{{E_0}}}{{\sqrt 2}}\sqrt {{V^2} _1 + {{({V_2} - {V_1})} ^2}} $
$ \Rightarrow {\varepsilon _0} = \dfrac{{{E_0}}}{{\sqrt 2}}\sqrt {{{40} ^2} + {{(40 - 10)} ^2}} $
$ \Rightarrow {\varepsilon _0} = 50V$
Now,
${X_L} = (\omega L) = \dfrac{{{V_2}}}{{{i_{rms}}}}$
Where, ${X_L} $ is Inductive Reactance
$ \Rightarrow {X_L} = 4\Omega $
$L = \dfrac{4}{\omega} = \dfrac{4}{{100\pi}}H $
$ \Rightarrow L = \dfrac{1}{{25\pi}}$
Where, ${X_C} $ is Capacitive Reactance
${X_C} = \omega C = \dfrac{{{V_1}}}{{{i_{rms}}}}$
$ \Rightarrow {X_C} = 1\Omega $
$ \Rightarrow C = \dfrac{1}{\omega} = \dfrac{1}{{100\pi}}F $
Note: By squaring speeds and taking the square root, we conquer the 'directional' component of speed and at the same time achieve the average speed of the particles. As the value lacks the trajectory of the particles, the average speed is now referred to as the value. Root-medium-square velocity is the calculation of particle speed in a gas described by the square root of the average molecular velocity square of a gas.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding Uniform Acceleration in Physics

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding Electromagnetic Waves and Their Importance

Understanding the Electric Field of a Uniformly Charged Ring

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry




