
Prove the following expression:
\[\underset{n\to \infty }{\mathop{\lim \text{it}}}\,\dfrac{1}{n}\left[ {{\cos }^{2p}}\dfrac{\pi }{2n}+{{\cos }^{2p}}\dfrac{2\pi }{2n}+{{\cos }^{2p}}\dfrac{3\pi }{2n}+{{\cos }^{2p}}\dfrac{\pi }{2} \right]=\underset{r=1}{\overset{p}{\mathop{\prod }}}\,\dfrac{p+r}{4r}\]
Answer
506k+ views
Hint: Apply reverse of limit as a sum means converting any infinite series to integral form. Find $\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx}$ using integration by parts by splitting ${{\cos }^{n}}x$ to $\cos x\ and\ {{\cos }^{n-1}}x$.
Here, we have the limit given to calculate is
\[\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{\cos }^{2p}}\dfrac{\pi }{2n}+{{\cos }^{2p}}\dfrac{2\pi }{2n}+{{\cos }^{2p}}\dfrac{3\pi }{2n}+......{{\cos }^{2p}}\dfrac{n\pi }{2n} \right]\]which should be equal to given result \[\underset{r=1}{\overset{p}{\mathop{\prod }}}\,\dfrac{p+r}{4r}\]i.e.,
$\left( \dfrac{p+1}{4} \right)\left( \dfrac{p+2}{4.2} \right)\left( \dfrac{p+3}{4.3} \right)......\left( \dfrac{2p}{4.p} \right)$
Let us first calculate LHS part of the given equation;
\[\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{\cos }^{2p}}\dfrac{\pi }{2n}+{{\cos }^{2p}}\dfrac{2\pi }{2n}+{{\cos }^{2p}}\dfrac{3\pi }{2n}+......{{\cos }^{2p}}\dfrac{n\pi }{2n} \right]..........\left( 1 \right)\]
Here, we can put a direct limit to the function, and we cannot find summation of the given series (very complex). We cannot put a limit because the number of times is not defined.
So, here we need to apply limits as a sum rule of integration.
Basic definition of limit as a sum that if we want to find integration of any function then we can break that function into infinite sums;
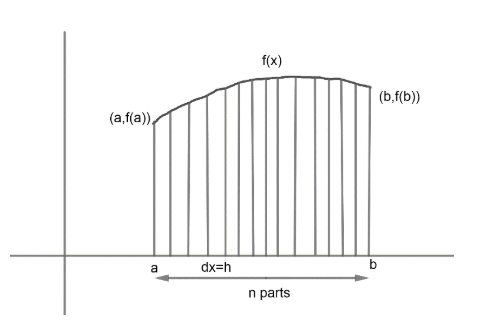
$\left( h=\dfrac{b-a}{n} \right)$
We can write $\int_{a}^{b}{f\left( x \right)}dx$ to sum of area of very short intervals of length ‘h’, and can be expressed
$\int_{a}^{b}{f\left( x \right)}dx=hf\left( a \right)+hf\left( a+h \right)+hf\left( a+2h \right)+....hf\left( a+\left( n-1 \right)h \right)$
Where h(f(a)), hf(a+h)………hf(a+(n-1)h) are areas of rectangles formed.
$\int_{a}^{b}{f\left( x \right)dx=\left( b-a \right)\underset{n\to \infty }{\mathop{\lim }}\,}\dfrac{1}{n}\left( f\left( a \right)+f\left( a+h \right)+.......f\left( a+\left( n-1 \right)d \right) \right)$
We can observe that reverse of the limit as a sum of integration should also be true and expressed as follows;
Above given series can be written as;
$\int_{a}^{b}{f\left( x \right)dx=\underset{n\to \infty }{\mathop{\lim }}\,}\dfrac{b-a}{n}\sum\limits_{r=0}^{n}{f\left( a+rh \right)}$
We have, $h=\dfrac{b-a}{n}$
$\int_{a}^{b}{f\left( x \right)dx=\underset{h\to 0}{\mathop{\lim }}\,}h\sum\limits_{r=0}^{n=\dfrac{\left( b-a \right)}{h}}{f\left( a+rh \right)}$
By comparison, of the above equation, we can get the reverse of the above as well.
Let us suppose we have series given as;
\[\begin{align}
& \underset{n\to \infty }{\mathop{\dfrac{b-a}{n}}}\,\sum\limits_{r=0}^{n}{f\left( a+\left( b-a \right)\dfrac{r}{n} \right)}=\underset{n\to \infty }{\mathop{\dfrac{b-a}{n}}}\,\left[ f\left( a \right)+f\left( a+\dfrac{\left( b-a \right)}{n} \right)+.......f\left( a+\dfrac{\left( b-a \right)n}{n} \right) \right] \\
& \int_{a}^{b}{f\left( x \right)dx} \\
\end{align}\]
Let we have \[\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\sum\limits_{r=1}^{n}{f\left( a+\dfrac{r}{h} \right)}\]
Hence, we need to convert given series to integral form by changing
\[\begin{align}
& \dfrac{1}{n}\to dx \\
& \dfrac{r}{n}\to x \\
\end{align}\]
Lower limit \[=\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{r}{n}\]
Upper limit = put r = n in $\left( \dfrac{r}{n} \right)$ i.e. maximum value of r.
Now, coming to the question, we have
\[\begin{align}
& \underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{\cos }^{2p}}\dfrac{\pi }{2n}+{{\cos }^{2p}}\dfrac{2\pi }{2n}+{{\cos }^{2p}}\dfrac{3\pi }{2n}+......{{\cos }^{2p}}\dfrac{n\pi }{2n} \right] \\
& \underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\sum\limits_{r=1}^{n}{{{\cos }^{2p}}\dfrac{r\pi }{2n}} \\
\end{align}\]
Here, we need to replace $\dfrac{1}{n}$ by dx, \[\dfrac{r}{n}\]by x,
Lower limit \[=n\to \infty \dfrac{r}{n}=0\]
Upper limit = r = n in $\dfrac{r}{n}=1$
Hence, we can write the given series in integral form;
$\int_{0}^{1}{{{\cos }^{2p}}\left( \dfrac{\pi x}{2} \right)dx}$
Now, we need to solve above integration as;
$I=\int_{0}^{1}{{{\cos }^{2p}}\dfrac{\pi x}{2}}dx$
Let \[\dfrac{\pi x}{2}=t\]
Differentiating both sides;
\[\begin{align}
& \dfrac{\pi }{2}\dfrac{dx}{dt}=1 \\
& dx=\dfrac{2}{\pi }dt \\
\end{align}\]
Lower limit w.r.t. t is =0
Upper limit w.r.t. t is \[\dfrac{\pi }{2}\]
$I=\dfrac{2}{\pi }\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2p}}t}dt$
Taking n = 2p, we get
$I=\dfrac{2}{\pi }\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}t}dt$………………… (2)
Now, we have to find $\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}t}dt$, so that we can put it to equation (2) to get answer.
\[\begin{align}
& {{I}_{n}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}x}dx................\left( 3 \right) \\
& =\int_{0}^{\dfrac{\pi }{2}}{\cos x}{{\cos }^{n-1}}xdx \\
\end{align}\]
Apply integration by parts as;
If we have two functions in multiplication then we have,
$\int{f\left( x \right)g\left( x \right)=f\left( x \right)\int{g\left( x \right)-\int{f'\left( x \right)}}}\int{g\left( x \right)}$
Here $f\left( x \right)={{\cos }^{n-1}}x\And g\left( x \right)=\cos x$
Hence,
\[\begin{align}
& {{I}_{n}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx=}\int_{0}^{\dfrac{\pi }{2}}{\cos x{{\cos }^{n-1}}xdx} \\
& {{I}_{n}}=\int_{0}^{\dfrac{\pi }{2}}{\cos x{{\cos }^{n-1}}xdx} \\
\end{align}\]
\[\begin{align}
& {{I}_{n}}={{\cos }^{n-1}}x\int_{0}^{\dfrac{\pi }{2}}{\cos xdx-}\int_{0}^{\dfrac{\pi }{2}}{\dfrac{d }{dx}{{\cos }^{n-1}}x}\int{\cos xdx.dx} \\
& {{I}_{n}}={{\cos }^{n-1}}x\sin x\left| \begin{matrix}
\dfrac{\pi }{2} \\
0 \\
\end{matrix} \right.+\int_{0}^{\dfrac{\pi }{2}}{\left( n-1 \right)}{{\cos }^{n-2}}x\sin x.\sin xdx \\
& {{I}_{n}}=0+\left( n-1 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}{{\sin }^{2}}xdx \\
& {{I}_{n}}=\left( n-1 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}\left( 1-{{\cos }^{2}}x \right)dx \\
& {{I}_{n}}=\left( n-1 \right)\left( \int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx-\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx} \right) \\
\end{align}\]
We have \[In=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx}\]from equation (3)
\[\begin{align}
& {{I}_{n}}=\left( n-1 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx-{{I}_{n}}\left( n-1 \right) \\
& {{I}_{n}}=\left( \dfrac{n-1}{n} \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx \\
& {{I}_{n}}=\left( \dfrac{n-1}{n} \right){{I}_{n-2}}..............\left( 4 \right) \\
\end{align}\]
Let us calculate ${{I}_{n-2}}$ in similar way;
\[\begin{align}
& {{I}_{n-2}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx..............\left( 5 \right) \\
& {{I}_{n-2}}=\int_{0}^{\dfrac{\pi }{2}}{\cos x}{{\cos }^{n-3}}xdx \\
\end{align}\]
Applying integration by parts here as well, we get;
\[\begin{align}
& {{I}_{n-2}}={{\cos }^{n-3}}x\int_{0}^{\dfrac{\pi }{2}}{\cos x}dx-\int{\dfrac{d}{dx}}\left( {{\cos }^{n-3}}x \right).\int{\cos xdx.dx} \\
& {{I}_{n-2}}={{\cos }^{n-3}}x\sin x\left| \begin{matrix}
\dfrac{\pi }{2} \\
0 \\
\end{matrix} \right.\int_{0}^{\dfrac{\pi }{2}}{\left( n-3 \right){{\cos }^{n-4}}x}{{\sin }^{2}}xdx \\
& {{I}_{n-2}}=0+\left( n-3 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-4}}x}{{\sin }^{2}}xdx \\
& {{I}_{n-2}}=\left( n-3 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-4}}x}\left( 1-{{\cos }^{2}}x \right)dx \\
& {{I}_{n-2}}=\left( n-3 \right)\left[ \int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-4}}x}dx-\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx \right] \\
\end{align}\]
Since,\[{{I}_{n-2}}\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx\] from equation (5)
\[\begin{align}
& {{I}_{n-2}}=\left( n-3 \right)\left[ \int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-4}}x}dx-{{I}_{n-4}} \right] \\
& {{I}_{n-2}}=\left( \dfrac{n-3}{n-2} \right){{I}_{n-4}}.............\left( 6 \right) \\
\end{align}\]
Now, from equation (4), (5), (6) we have
${{I}_{n}}=\left( \dfrac{n-1}{n} \right)\left( \dfrac{n-3}{n-2} \right){{I}_{n-4}}$
Similarly,
${{I}_{n-4}}=\left( \dfrac{n-5}{n-4} \right){{I}_{n}}=6$
Hence, we can generalize the above integration as
${{I}_{n}}=\left( \dfrac{n-1}{n} \right)\left( \dfrac{n-3}{n-2} \right)\left( \dfrac{n-5}{n-4} \right)..........$
Now, we can observe that answer will depend if n is odd or even.
If n is odd then at last stage we get ${{I}_{3}}\And {{I}_{1}}$ and if n is even then at last stage we get ${{I}_{2}}$
$\begin{align}
& {{I}_{1}}=\int_{0}^{\dfrac{\pi }{2}}{\cos xdx=\sin x}\int_{0}^{\dfrac{\pi }{2}}{=1} \\
& {{I}_{2}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2}}xdx=}\int_{0}^{\dfrac{\pi }{2}}{\dfrac{1-{{\cos }^{2}}x}{2}} \\
& =\left( \dfrac{x}{2}-\dfrac{1}{2}\dfrac{{{\sin }^{2}}x}{2} \right)\begin{matrix}
\dfrac{\pi }{2} \\
0 \\
\end{matrix} \\
& {{I}_{2}}=\dfrac{\pi }{4}-\dfrac{1}{2}\times \left( 0 \right)=\dfrac{\pi }{4} \\
\end{align}$
Hence, the above relation can be written as;
${{I}_{n}}=\left( \dfrac{n-1}{n} \right)\left( \dfrac{n-3}{n-2} \right).........\dfrac{2}{3}\left( 1 \right)$ if n is odd
${{I}_{n}}=\left( \dfrac{n-1}{n} \right)\left( \dfrac{n-3}{n-2} \right).........\dfrac{7}{8}\dfrac{5}{6}\dfrac{\pi }{4}$ if n is even
Now, coming back to the integration
$\dfrac{2}{\pi }\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2p}}+dt}$, here n = 2p is an even number.
Hence, we can write the above integral as
\[I=\dfrac{2}{\pi }\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2p}}tdt=}\dfrac{2}{\pi }\left( \left( \dfrac{2p-1}{2p} \right)\left( \dfrac{2p-3}{2p-2} \right)\left( \dfrac{2p-5}{2p-4} \right).....\dfrac{7}{8}.\dfrac{5}{6}.\dfrac{3}{4}.\dfrac{\pi }{4} \right)\]
Using the integral ${{I}_{2}}=\dfrac{\pi }{4}$ as calculated in equation,
\[I=\left( \dfrac{2p-1}{2p} \right)\left( \dfrac{2p-3}{2p-2} \right)\left( \dfrac{2p-5}{2p-4} \right).....\left( \dfrac{5}{6} \right)\left( \dfrac{3}{4} \right)\left( \dfrac{1}{2} \right)\]
Multiply by (2p) (2p-2) (2p-4) …..6.4.2 in numerator and denominator as
\[\begin{align}
& I=\dfrac{\left( 2p \right)\left( 2p-1 \right)\left( 2p-2 \right)\left( 2p-3 \right).....5.4.3.2.1}{{{\left( 2p.\left( 2p-2 \right)\left( 2p-4 \right)......6.4.2 \right)}^{2}}} \\
& I=\dfrac{\left( 2p \right)!}{{{\left( {{2}^{p}}.p\left( p-1 \right)\left( p-2 \right).....3.2.1 \right)}^{2}}} \\
& I=\dfrac{\left( 2p \right)!}{{{2}^{2p}}.{{\left( p! \right)}^{2}}}=\dfrac{2p!}{{{4}^{p}}p!p!} \\
\end{align}\]
Now, let us calculated $\left( 2p \right)!$ as below;
$\begin{align}
& \left( 2p \right)!=\left( 2p \right)\left( 2p-1 \right).......\left( 2p-p \right)\left( 2p-p-1 \right).......3.2.1 \\
& Or \\
& \left( 2p \right)!=\left( 2p \right)\left( 2p-1 \right).......\left( p \right)\left( p-1 \right).......3.2.1 \\
\end{align}$
Let us write the above series in reverse order;
$\begin{align}
& \left( 2p \right)!=1.2.3.4.....\left( p-1 \right)p\left( p+1 \right)\left( p+2 \right)\left( p+p \right) \\
& \left( 2p \right)!=\left( 1.2.3.4....p \right)\left( p+1 \right)\left( p+2 \right)\left( p+p \right) \\
\end{align}$
Let us substitute the above value of $\left( 2p \right)!$ in equation
$\begin{align}
& I=\dfrac{\left( 1.2.3.4....p \right)\left( p+1 \right)\left( p+2 \right)\left( p+p \right)}{{{4}^{p}}.p!p!} \\
& Or \\
& I=\dfrac{p!\left( p+1 \right)\left( p+2 \right)\left( p+3 \right)...........\left( p+p \right)}{{{4}^{p}}.p!p!} \\
& I=\dfrac{\left( p+1 \right)\left( p+2 \right)\left( p+3 \right)...........\left( p+p \right)}{{{4}^{p}}.p!} \\
\end{align}$
We can write the above expression as
$\begin{align}
& I=\left( \dfrac{p+1}{4.1} \right)\left( \dfrac{p+2}{4.2} \right)\left( \dfrac{p+3}{4.3} \right)......\left( \dfrac{p+p}{4.p} \right) \\
& I=\underset{r=1}{\overset{p}{\mathop{\prod }}}\,\dfrac{p+r}{4r}=RHS \\
\end{align}$
Hence Proved.
Note: Calculation plays an important role in these types of subjective problems.
One can go wrong while changing the given series to integral. Limits of integral will be a key point of further solution.
In limit as a sum, we need to replace
\[\begin{align}
& \dfrac{1}{n}\to dx \\
& \dfrac{r}{n}\to x \\
\end{align}\]
Lower limit \[=n\to \infty \text{ to }\left( \dfrac{r}{n} \right)\text{ part}\]
Upper limit = put r = maximum value of n in $\left( \dfrac{r}{n} \right)$.
One can waste his/her time when even thinking that this is a problem of limit and differentiability chapter.
Integration of $\int_{0}^{\dfrac{\pi }{2}}{\cos xdx\And }\int_{0}^{\dfrac{\pi }{2}}{{{\sin }^{n}}x}dx$need to remember as
${{I}_{n}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx}=\left( \dfrac{n-1}{n} \right){{I}_{n-2}}$
Here, we have the limit given to calculate is
\[\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{\cos }^{2p}}\dfrac{\pi }{2n}+{{\cos }^{2p}}\dfrac{2\pi }{2n}+{{\cos }^{2p}}\dfrac{3\pi }{2n}+......{{\cos }^{2p}}\dfrac{n\pi }{2n} \right]\]which should be equal to given result \[\underset{r=1}{\overset{p}{\mathop{\prod }}}\,\dfrac{p+r}{4r}\]i.e.,
$\left( \dfrac{p+1}{4} \right)\left( \dfrac{p+2}{4.2} \right)\left( \dfrac{p+3}{4.3} \right)......\left( \dfrac{2p}{4.p} \right)$
Let us first calculate LHS part of the given equation;
\[\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{\cos }^{2p}}\dfrac{\pi }{2n}+{{\cos }^{2p}}\dfrac{2\pi }{2n}+{{\cos }^{2p}}\dfrac{3\pi }{2n}+......{{\cos }^{2p}}\dfrac{n\pi }{2n} \right]..........\left( 1 \right)\]
Here, we can put a direct limit to the function, and we cannot find summation of the given series (very complex). We cannot put a limit because the number of times is not defined.
So, here we need to apply limits as a sum rule of integration.
Basic definition of limit as a sum that if we want to find integration of any function then we can break that function into infinite sums;

$\left( h=\dfrac{b-a}{n} \right)$
We can write $\int_{a}^{b}{f\left( x \right)}dx$ to sum of area of very short intervals of length ‘h’, and can be expressed
$\int_{a}^{b}{f\left( x \right)}dx=hf\left( a \right)+hf\left( a+h \right)+hf\left( a+2h \right)+....hf\left( a+\left( n-1 \right)h \right)$
Where h(f(a)), hf(a+h)………hf(a+(n-1)h) are areas of rectangles formed.
$\int_{a}^{b}{f\left( x \right)dx=\left( b-a \right)\underset{n\to \infty }{\mathop{\lim }}\,}\dfrac{1}{n}\left( f\left( a \right)+f\left( a+h \right)+.......f\left( a+\left( n-1 \right)d \right) \right)$
We can observe that reverse of the limit as a sum of integration should also be true and expressed as follows;
Above given series can be written as;
$\int_{a}^{b}{f\left( x \right)dx=\underset{n\to \infty }{\mathop{\lim }}\,}\dfrac{b-a}{n}\sum\limits_{r=0}^{n}{f\left( a+rh \right)}$
We have, $h=\dfrac{b-a}{n}$
$\int_{a}^{b}{f\left( x \right)dx=\underset{h\to 0}{\mathop{\lim }}\,}h\sum\limits_{r=0}^{n=\dfrac{\left( b-a \right)}{h}}{f\left( a+rh \right)}$
By comparison, of the above equation, we can get the reverse of the above as well.
Let us suppose we have series given as;
\[\begin{align}
& \underset{n\to \infty }{\mathop{\dfrac{b-a}{n}}}\,\sum\limits_{r=0}^{n}{f\left( a+\left( b-a \right)\dfrac{r}{n} \right)}=\underset{n\to \infty }{\mathop{\dfrac{b-a}{n}}}\,\left[ f\left( a \right)+f\left( a+\dfrac{\left( b-a \right)}{n} \right)+.......f\left( a+\dfrac{\left( b-a \right)n}{n} \right) \right] \\
& \int_{a}^{b}{f\left( x \right)dx} \\
\end{align}\]
Let we have \[\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\sum\limits_{r=1}^{n}{f\left( a+\dfrac{r}{h} \right)}\]
Hence, we need to convert given series to integral form by changing
\[\begin{align}
& \dfrac{1}{n}\to dx \\
& \dfrac{r}{n}\to x \\
\end{align}\]
Lower limit \[=\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{r}{n}\]
Upper limit = put r = n in $\left( \dfrac{r}{n} \right)$ i.e. maximum value of r.
Now, coming to the question, we have
\[\begin{align}
& \underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{\cos }^{2p}}\dfrac{\pi }{2n}+{{\cos }^{2p}}\dfrac{2\pi }{2n}+{{\cos }^{2p}}\dfrac{3\pi }{2n}+......{{\cos }^{2p}}\dfrac{n\pi }{2n} \right] \\
& \underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\sum\limits_{r=1}^{n}{{{\cos }^{2p}}\dfrac{r\pi }{2n}} \\
\end{align}\]
Here, we need to replace $\dfrac{1}{n}$ by dx, \[\dfrac{r}{n}\]by x,
Lower limit \[=n\to \infty \dfrac{r}{n}=0\]
Upper limit = r = n in $\dfrac{r}{n}=1$
Hence, we can write the given series in integral form;
$\int_{0}^{1}{{{\cos }^{2p}}\left( \dfrac{\pi x}{2} \right)dx}$
Now, we need to solve above integration as;
$I=\int_{0}^{1}{{{\cos }^{2p}}\dfrac{\pi x}{2}}dx$
Let \[\dfrac{\pi x}{2}=t\]
Differentiating both sides;
\[\begin{align}
& \dfrac{\pi }{2}\dfrac{dx}{dt}=1 \\
& dx=\dfrac{2}{\pi }dt \\
\end{align}\]
Lower limit w.r.t. t is =0
Upper limit w.r.t. t is \[\dfrac{\pi }{2}\]
$I=\dfrac{2}{\pi }\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2p}}t}dt$
Taking n = 2p, we get
$I=\dfrac{2}{\pi }\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}t}dt$………………… (2)
Now, we have to find $\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}t}dt$, so that we can put it to equation (2) to get answer.
\[\begin{align}
& {{I}_{n}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}x}dx................\left( 3 \right) \\
& =\int_{0}^{\dfrac{\pi }{2}}{\cos x}{{\cos }^{n-1}}xdx \\
\end{align}\]
Apply integration by parts as;
If we have two functions in multiplication then we have,
$\int{f\left( x \right)g\left( x \right)=f\left( x \right)\int{g\left( x \right)-\int{f'\left( x \right)}}}\int{g\left( x \right)}$
Here $f\left( x \right)={{\cos }^{n-1}}x\And g\left( x \right)=\cos x$
Hence,
\[\begin{align}
& {{I}_{n}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx=}\int_{0}^{\dfrac{\pi }{2}}{\cos x{{\cos }^{n-1}}xdx} \\
& {{I}_{n}}=\int_{0}^{\dfrac{\pi }{2}}{\cos x{{\cos }^{n-1}}xdx} \\
\end{align}\]
\[\begin{align}
& {{I}_{n}}={{\cos }^{n-1}}x\int_{0}^{\dfrac{\pi }{2}}{\cos xdx-}\int_{0}^{\dfrac{\pi }{2}}{\dfrac{d }{dx}{{\cos }^{n-1}}x}\int{\cos xdx.dx} \\
& {{I}_{n}}={{\cos }^{n-1}}x\sin x\left| \begin{matrix}
\dfrac{\pi }{2} \\
0 \\
\end{matrix} \right.+\int_{0}^{\dfrac{\pi }{2}}{\left( n-1 \right)}{{\cos }^{n-2}}x\sin x.\sin xdx \\
& {{I}_{n}}=0+\left( n-1 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}{{\sin }^{2}}xdx \\
& {{I}_{n}}=\left( n-1 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}\left( 1-{{\cos }^{2}}x \right)dx \\
& {{I}_{n}}=\left( n-1 \right)\left( \int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx-\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx} \right) \\
\end{align}\]
We have \[In=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx}\]from equation (3)
\[\begin{align}
& {{I}_{n}}=\left( n-1 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx-{{I}_{n}}\left( n-1 \right) \\
& {{I}_{n}}=\left( \dfrac{n-1}{n} \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx \\
& {{I}_{n}}=\left( \dfrac{n-1}{n} \right){{I}_{n-2}}..............\left( 4 \right) \\
\end{align}\]
Let us calculate ${{I}_{n-2}}$ in similar way;
\[\begin{align}
& {{I}_{n-2}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx..............\left( 5 \right) \\
& {{I}_{n-2}}=\int_{0}^{\dfrac{\pi }{2}}{\cos x}{{\cos }^{n-3}}xdx \\
\end{align}\]
Applying integration by parts here as well, we get;
\[\begin{align}
& {{I}_{n-2}}={{\cos }^{n-3}}x\int_{0}^{\dfrac{\pi }{2}}{\cos x}dx-\int{\dfrac{d}{dx}}\left( {{\cos }^{n-3}}x \right).\int{\cos xdx.dx} \\
& {{I}_{n-2}}={{\cos }^{n-3}}x\sin x\left| \begin{matrix}
\dfrac{\pi }{2} \\
0 \\
\end{matrix} \right.\int_{0}^{\dfrac{\pi }{2}}{\left( n-3 \right){{\cos }^{n-4}}x}{{\sin }^{2}}xdx \\
& {{I}_{n-2}}=0+\left( n-3 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-4}}x}{{\sin }^{2}}xdx \\
& {{I}_{n-2}}=\left( n-3 \right)\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-4}}x}\left( 1-{{\cos }^{2}}x \right)dx \\
& {{I}_{n-2}}=\left( n-3 \right)\left[ \int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-4}}x}dx-\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx \right] \\
\end{align}\]
Since,\[{{I}_{n-2}}\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-2}}x}dx\] from equation (5)
\[\begin{align}
& {{I}_{n-2}}=\left( n-3 \right)\left[ \int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n-4}}x}dx-{{I}_{n-4}} \right] \\
& {{I}_{n-2}}=\left( \dfrac{n-3}{n-2} \right){{I}_{n-4}}.............\left( 6 \right) \\
\end{align}\]
Now, from equation (4), (5), (6) we have
${{I}_{n}}=\left( \dfrac{n-1}{n} \right)\left( \dfrac{n-3}{n-2} \right){{I}_{n-4}}$
Similarly,
${{I}_{n-4}}=\left( \dfrac{n-5}{n-4} \right){{I}_{n}}=6$
Hence, we can generalize the above integration as
${{I}_{n}}=\left( \dfrac{n-1}{n} \right)\left( \dfrac{n-3}{n-2} \right)\left( \dfrac{n-5}{n-4} \right)..........$
Now, we can observe that answer will depend if n is odd or even.
If n is odd then at last stage we get ${{I}_{3}}\And {{I}_{1}}$ and if n is even then at last stage we get ${{I}_{2}}$
$\begin{align}
& {{I}_{1}}=\int_{0}^{\dfrac{\pi }{2}}{\cos xdx=\sin x}\int_{0}^{\dfrac{\pi }{2}}{=1} \\
& {{I}_{2}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2}}xdx=}\int_{0}^{\dfrac{\pi }{2}}{\dfrac{1-{{\cos }^{2}}x}{2}} \\
& =\left( \dfrac{x}{2}-\dfrac{1}{2}\dfrac{{{\sin }^{2}}x}{2} \right)\begin{matrix}
\dfrac{\pi }{2} \\
0 \\
\end{matrix} \\
& {{I}_{2}}=\dfrac{\pi }{4}-\dfrac{1}{2}\times \left( 0 \right)=\dfrac{\pi }{4} \\
\end{align}$
Hence, the above relation can be written as;
${{I}_{n}}=\left( \dfrac{n-1}{n} \right)\left( \dfrac{n-3}{n-2} \right).........\dfrac{2}{3}\left( 1 \right)$ if n is odd
${{I}_{n}}=\left( \dfrac{n-1}{n} \right)\left( \dfrac{n-3}{n-2} \right).........\dfrac{7}{8}\dfrac{5}{6}\dfrac{\pi }{4}$ if n is even
Now, coming back to the integration
$\dfrac{2}{\pi }\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2p}}+dt}$, here n = 2p is an even number.
Hence, we can write the above integral as
\[I=\dfrac{2}{\pi }\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2p}}tdt=}\dfrac{2}{\pi }\left( \left( \dfrac{2p-1}{2p} \right)\left( \dfrac{2p-3}{2p-2} \right)\left( \dfrac{2p-5}{2p-4} \right).....\dfrac{7}{8}.\dfrac{5}{6}.\dfrac{3}{4}.\dfrac{\pi }{4} \right)\]
Using the integral ${{I}_{2}}=\dfrac{\pi }{4}$ as calculated in equation,
\[I=\left( \dfrac{2p-1}{2p} \right)\left( \dfrac{2p-3}{2p-2} \right)\left( \dfrac{2p-5}{2p-4} \right).....\left( \dfrac{5}{6} \right)\left( \dfrac{3}{4} \right)\left( \dfrac{1}{2} \right)\]
Multiply by (2p) (2p-2) (2p-4) …..6.4.2 in numerator and denominator as
\[\begin{align}
& I=\dfrac{\left( 2p \right)\left( 2p-1 \right)\left( 2p-2 \right)\left( 2p-3 \right).....5.4.3.2.1}{{{\left( 2p.\left( 2p-2 \right)\left( 2p-4 \right)......6.4.2 \right)}^{2}}} \\
& I=\dfrac{\left( 2p \right)!}{{{\left( {{2}^{p}}.p\left( p-1 \right)\left( p-2 \right).....3.2.1 \right)}^{2}}} \\
& I=\dfrac{\left( 2p \right)!}{{{2}^{2p}}.{{\left( p! \right)}^{2}}}=\dfrac{2p!}{{{4}^{p}}p!p!} \\
\end{align}\]
Now, let us calculated $\left( 2p \right)!$ as below;
$\begin{align}
& \left( 2p \right)!=\left( 2p \right)\left( 2p-1 \right).......\left( 2p-p \right)\left( 2p-p-1 \right).......3.2.1 \\
& Or \\
& \left( 2p \right)!=\left( 2p \right)\left( 2p-1 \right).......\left( p \right)\left( p-1 \right).......3.2.1 \\
\end{align}$
Let us write the above series in reverse order;
$\begin{align}
& \left( 2p \right)!=1.2.3.4.....\left( p-1 \right)p\left( p+1 \right)\left( p+2 \right)\left( p+p \right) \\
& \left( 2p \right)!=\left( 1.2.3.4....p \right)\left( p+1 \right)\left( p+2 \right)\left( p+p \right) \\
\end{align}$
Let us substitute the above value of $\left( 2p \right)!$ in equation
$\begin{align}
& I=\dfrac{\left( 1.2.3.4....p \right)\left( p+1 \right)\left( p+2 \right)\left( p+p \right)}{{{4}^{p}}.p!p!} \\
& Or \\
& I=\dfrac{p!\left( p+1 \right)\left( p+2 \right)\left( p+3 \right)...........\left( p+p \right)}{{{4}^{p}}.p!p!} \\
& I=\dfrac{\left( p+1 \right)\left( p+2 \right)\left( p+3 \right)...........\left( p+p \right)}{{{4}^{p}}.p!} \\
\end{align}$
We can write the above expression as
$\begin{align}
& I=\left( \dfrac{p+1}{4.1} \right)\left( \dfrac{p+2}{4.2} \right)\left( \dfrac{p+3}{4.3} \right)......\left( \dfrac{p+p}{4.p} \right) \\
& I=\underset{r=1}{\overset{p}{\mathop{\prod }}}\,\dfrac{p+r}{4r}=RHS \\
\end{align}$
Hence Proved.
Note: Calculation plays an important role in these types of subjective problems.
One can go wrong while changing the given series to integral. Limits of integral will be a key point of further solution.
In limit as a sum, we need to replace
\[\begin{align}
& \dfrac{1}{n}\to dx \\
& \dfrac{r}{n}\to x \\
\end{align}\]
Lower limit \[=n\to \infty \text{ to }\left( \dfrac{r}{n} \right)\text{ part}\]
Upper limit = put r = maximum value of n in $\left( \dfrac{r}{n} \right)$.
One can waste his/her time when even thinking that this is a problem of limit and differentiability chapter.
Integration of $\int_{0}^{\dfrac{\pi }{2}}{\cos xdx\And }\int_{0}^{\dfrac{\pi }{2}}{{{\sin }^{n}}x}dx$need to remember as
${{I}_{n}}=\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{n}}xdx}=\left( \dfrac{n-1}{n} \right){{I}_{n-2}}$
Recently Updated Pages
Alpha, Beta, and Gamma Decay Explained

Alpha Particle Scattering and Rutherford Model Explained

Angular Momentum of a Rotating Body: Definition & Formula

Apparent Frequency Explained: Formula, Uses & Examples

Applications of Echo in Daily Life and Science

Block and Tackle System: Definition, Types & Examples

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Correction Window 2026 Session 1 Dates Announced - Edit Form Details, Dates and Link

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Atomic Structure: Definition, Models, and Examples

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Average and RMS Value in Physics: Formula, Comparison & Application

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry




