Question

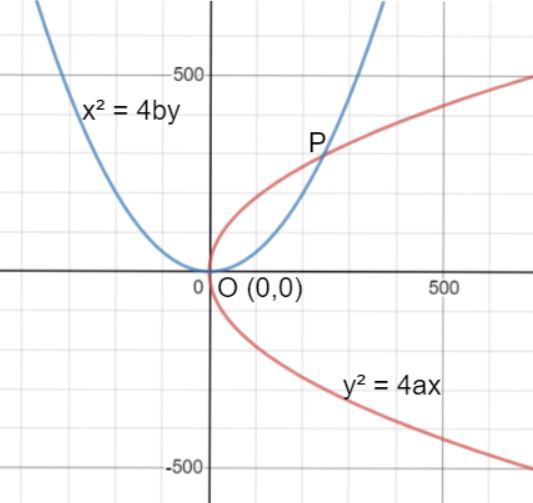
Prove that the two parabolas $ {y^2} = 4ax $ and $ {x^2} = 4by $ intersect (other than the origin) at an angle of \[{\tan ^{ - 1}}\left[ {\dfrac{{3{a^{\dfrac{1}{3}}}{b^{\dfrac{1}{3}}}}}{{2\left( {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} \right)}}} \right]\].

Answer 1

Hint: Here, we will proceed by firstly finding the points of intersection of the given parabolas and then we will find the slopes of tangent of these two curves at the intersection point other than origin and then apply the formula $ \tan \theta = \dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}} $ .

Complete step-by-step answer:
Equations of the given parabolas are $ {y^2} = 4ax{\text{ }} \to (1) $ and $ {x^2} = 4by{\text{ }} \to {\text{(2)}} $
Equation (2) can be rewritten as $ y = \dfrac{{{x^2}}}{{4b}}{\text{ }} \to {\text{(3)}} $
By substituting the value of y from equation (3) in equation (1), we get
 $
   \Rightarrow {\left( {\dfrac{{{x^2}}}{{4b}}} \right)^2} = 4ax \\
   \Rightarrow \dfrac{{{x^4}}}{{16{b^2}}} = 4ax \\
  $
By cross multiplying the above equation, we get
 $
   \Rightarrow {x^4} = \left( {4ax} \right)\left( {16{b^2}} \right) \\
   \Rightarrow {x^4} = 64a{b^2}x \\
   \Rightarrow {x^4} - 64a{b^2}x = 0 \\
  $
By taking x common from the LHS of the above equation, we get
 $ \Rightarrow x\left( {{x^3} - 64a{b^2}} \right) = 0 $
Either $ x = 0 $ or $
  {x^3} - 64a{b^2} = 0 \\
   \Rightarrow {x^3} = 64a{b^2} \\
   \Rightarrow x = {\left( {64a{b^2}} \right)^{\dfrac{1}{3}}} = {\left( {64} \right)^{\dfrac{1}{3}}}{\left( a \right)^{\dfrac{1}{3}}}{\left( {{b^2}} \right)^{\dfrac{1}{3}}} \\
   \Rightarrow x = 4{a^{\dfrac{1}{3}}}{b^{\dfrac{2}{3}}} \\
  $
By putting x = 0 in equation (3), we get
 $ y = \dfrac{0}{{4b}} = 0 $
By putting $ x = 4{a^{\dfrac{1}{3}}}{b^{\dfrac{2}{3}}} $ in equation (3), we get
\[
   \Rightarrow y = \dfrac{{{{\left( {4{a^{\dfrac{1}{3}}}{b^{\dfrac{2}{3}}}} \right)}^2}}}{{4b}} = \dfrac{{16{a^{\dfrac{2}{3}}}{b^{\dfrac{4}{3}}}}}{{4b}} = 4{a^{\dfrac{2}{3}}}{b^{\dfrac{4}{3} - 1}} = 4{a^{\dfrac{2}{3}}}{b^{\dfrac{{4 - 3}}{3}}} \\
   \Rightarrow y = 4{a^{\dfrac{2}{3}}}{b^{\dfrac{1}{3}}} \\
 \]
So, the points of intersection of the given parabolas are O(0,0) and P $ \left( {4{a^{\dfrac{1}{3}}}{b^{\dfrac{2}{3}}},4{a^{\dfrac{2}{3}}}{b^{\dfrac{1}{3}}}} \right) $ .
As we know that the slope of the tangent to any curve is given by $ \dfrac{{dy}}{{dx}} $
By differentiating equation (1) on both sides with respect to x, we have
 $
   \Rightarrow \dfrac{d}{{dx}}\left( {{y^2}} \right) = \dfrac{d}{{dx}}\left( {4ax} \right) \\
   \Rightarrow 2y\dfrac{{dy}}{{dx}} = 4a\dfrac{{dx}}{{dx}} \\
  $
By taking 2y from the LHS to the RHS of the above equation, we get
 $
   \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{4a}}{{2y}} \\
   \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{2a}}{y} \\
  $
Slope of the tangent to the parabola $ {y^2} = 4ax $ at point P $ \left( {4{a^{\dfrac{1}{3}}}{b^{\dfrac{2}{3}}},4{a^{\dfrac{2}{3}}}{b^{\dfrac{1}{3}}}} \right) $ is given by
 $
   \Rightarrow {m_1} = \dfrac{{2a}}{{4{a^{\dfrac{2}{3}}}{b^{\dfrac{1}{3}}}}} = \dfrac{{{a^{1 - \dfrac{2}{3}}}}}{{2{b^{\dfrac{1}{3}}}}} = \dfrac{{{a^{\dfrac{{3 - 2}}{3}}}}}{{2{b^{\dfrac{1}{3}}}}} \\
   \Rightarrow {m_1} = \dfrac{{{a^{\dfrac{1}{3}}}}}{{2{b^{\dfrac{1}{3}}}}} \\
  $
By differentiating equation (2) on both sides with respect to x, we have
 $
   \Rightarrow \dfrac{d}{{dx}}\left( {{x^2}} \right) = \dfrac{d}{{dx}}\left( {4by} \right) \\
   \Rightarrow 2x\dfrac{{dx}}{{dx}} = 4b\dfrac{{dy}}{{dx}} \\
   \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{2x}}{{4b}} \\
   \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{x}{{2b}} \\
  $
Slope of the tangent to the parabola $ {x^2} = 4by $ at point P $ \left( {4{a^{\dfrac{1}{3}}}{b^{\dfrac{2}{3}}},4{a^{\dfrac{2}{3}}}{b^{\dfrac{1}{3}}}} \right) $ is given by
\[
   \Rightarrow {m_2} = \dfrac{x}{{2b}} = \dfrac{{4{a^{\dfrac{1}{3}}}{b^{\dfrac{2}{3}}}}}{{2b}} = \dfrac{{2{a^{\dfrac{1}{3}}}}}{{{b^{1 - \dfrac{2}{3}}}}} = \dfrac{{2{a^{\dfrac{1}{3}}}}}{{{b^{\dfrac{{3 - 2}}{3}}}}} \\
   \Rightarrow {m_2} = \dfrac{{2{a^{\dfrac{1}{3}}}}}{{{b^{\dfrac{1}{3}}}}} \\
 \]
Also, we know that the angle between any two curves having slopes of their tangents as \[{m_1}\] and \[{m_2}\] respectively at a point is given by
 $ \tan \theta = \dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}} $ where $ \theta $ is the angle between the curves
By putting $ {m_1} = \dfrac{{{a^{\dfrac{1}{3}}}}}{{2{b^{\dfrac{1}{3}}}}} $ and \[{m_2} = \dfrac{{2{a^{\dfrac{1}{3}}}}}{{{b^{\dfrac{1}{3}}}}}\] in the above formula, we get
 $ \Rightarrow \tan \theta = \dfrac{{\dfrac{{2{a^{\dfrac{1}{3}}}}}{{{b^{\dfrac{1}{3}}}}} - \dfrac{{{a^{\dfrac{1}{3}}}}}{{2{b^{\dfrac{1}{3}}}}}}}{{1 + \left( {\dfrac{{{a^{\dfrac{1}{3}}}}}{{2{b^{\dfrac{1}{3}}}}}} \right)\left( {\dfrac{{2{a^{\dfrac{1}{3}}}}}{{{b^{\dfrac{1}{3}}}}}} \right)}} $
By taking $ 2{b^{\dfrac{1}{3}}} $ as the LCM of the terms given in the numerator of the RHS of the above equation, we get
 $
   \Rightarrow \tan \theta = \dfrac{{\dfrac{{4{a^{\dfrac{1}{3}}} - {a^{\dfrac{1}{3}}}}}{{2{b^{\dfrac{1}{3}}}}}}}{{1 + \left( {\dfrac{{2{a^{\dfrac{1}{3}}}{a^{\dfrac{1}{3}}}}}{{2{b^{\dfrac{1}{3}}}{b^{\dfrac{1}{3}}}}}} \right)}} \\
   \Rightarrow \tan \theta = \dfrac{{\dfrac{{3{a^{\dfrac{1}{3}}}}}{{2{b^{\dfrac{1}{3}}}}}}}{{1 + \left( {\dfrac{{{a^{\dfrac{2}{3}}}}}{{{b^{\dfrac{2}{3}}}}}} \right)}} \\
  $
By taking $ {b^{\dfrac{2}{3}}} $ as the LCM of the terms given in the denominator of the RHS of the above equation, we get
 $
   \Rightarrow \tan \theta = \dfrac{{\dfrac{{3{a^{\dfrac{1}{3}}}}}{{2{b^{\dfrac{1}{3}}}}}}}{{\dfrac{{{b^{\dfrac{2}{3}}} + {a^{\dfrac{2}{3}}}}}{{{b^{\dfrac{2}{3}}}}}}} \\
   \Rightarrow \tan \theta = \dfrac{{{b^{\dfrac{2}{3}}}\left( {3{a^{\dfrac{1}{3}}}} \right)}}{{2{b^{\dfrac{1}{3}}}\left( {{b^{\dfrac{2}{3}}} + {a^{\dfrac{2}{3}}}} \right)}} \\
   \Rightarrow \tan \theta = \dfrac{{3{b^{\dfrac{2}{3}}}{b^{\dfrac{{ - 1}}{3}}}\left( {{a^{\dfrac{1}{3}}}} \right)}}{{2\left( {{b^{\dfrac{2}{3}}} + {a^{\dfrac{2}{3}}}} \right)}} \\
   \Rightarrow \tan \theta = \dfrac{{3{b^{\dfrac{2}{3} - \dfrac{1}{3}}}\left( {{a^{\dfrac{1}{3}}}} \right)}}{{2\left( {{b^{\dfrac{2}{3}}} + {a^{\dfrac{2}{3}}}} \right)}} \\
   \Rightarrow \tan \theta = \dfrac{{3{a^{\dfrac{1}{3}}}{b^{\dfrac{1}{3}}}}}{{2\left( {{b^{\dfrac{2}{3}}} + {a^{\dfrac{2}{3}}}} \right)}} \\
  $
Taking inverse tangent trigonometric function on both sides of the above equation, we get
\[ \Rightarrow {\tan ^{ - 1}}\left( {\tan \theta } \right) = {\tan ^{ - 1}}\left[ {\dfrac{{3{a^{\dfrac{1}{3}}}{b^{\dfrac{1}{3}}}}}{{2\left( {{b^{\dfrac{2}{3}}} + {a^{\dfrac{2}{3}}}} \right)}}} \right]\]
Using the formula \[{\tan ^{ - 1}}\left( {\tan \theta } \right) = \theta \] in the above equation, we get
 \[ \Rightarrow \theta = {\tan ^{ - 1}}\left[ {\dfrac{{3{a^{\dfrac{1}{3}}}{b^{\dfrac{1}{3}}}}}{{2\left( {{b^{\dfrac{2}{3}}} + {a^{\dfrac{2}{3}}}} \right)}}} \right]\] where \[\theta \] represents the angle between the given parabolas $ {y^2} = 4ax $ and $ {x^2} = 4by $ at a point P $ \left( {4{a^{\dfrac{1}{3}}}{b^{\dfrac{2}{3}}},4{a^{\dfrac{2}{3}}}{b^{\dfrac{1}{3}}}} \right) $ where these two intersect (other than the origin).

Note- The point of intersection between any two curves can be found easily by solving for the values of x and y which will satisfy the equations of both the curves. Also, the slope of the tangent to any curve at a point P ( $ {x_1},{y_1} $ ) is evaluated by simply finding out $ \dfrac{{dy}}{{dx}} $ and then putting x = $ {x_1} $ and y = $ {y_1} $ in the expression obtained.