Questions & Answers
Question
Answers
Related Questions
Prove that the locus of the middle point of a portion of a normal intersected between the curve and the axis is a parabola whose vertex is the focus and whose latus rectum is one quarter of the original parabola.
Answer
![Verified]()
Verified
Verified
Hint: The equation of normal in parametric form is given as \[y=-tx+2at+a{{t}^{3}}\], where the normal is drawn at a point \[P\] with parameter \[t\].
First of all , let’s take the equation of the parabola to be \[{{y}^{2}}=4ax\].
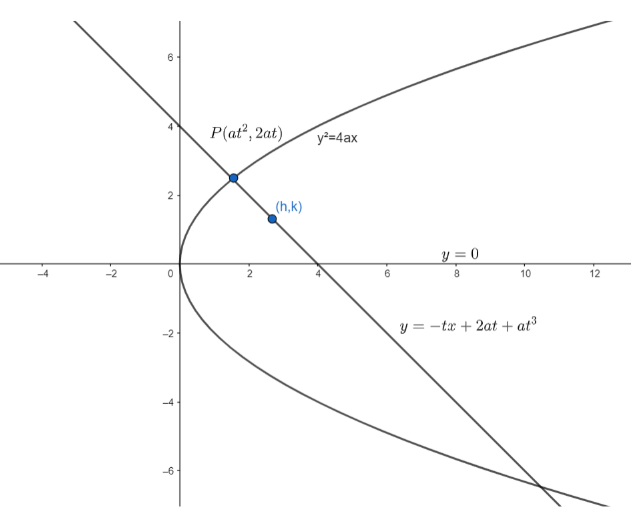
Coordinates of any point on the parabola in parametric form is given as \[P\left( a{{t}^{2}},2at \right)\].
We know, equation of normal in parametric form , where the normal is drawn at a point \[P\] with parameter \[t\], is given as
\[y=-tx+2at+a{{t}^{3}}....\left( i \right)\]
Also, the equation of axis of the parabola is
\[y=0.....\left( ii \right)\]
To find the points of intersection of \[\left( i \right)\]and\[\left( ii \right)\], we substitute \[y=0\] in \[\left( i \right)\].
So, \[0=-tx+2at+{{t}^{3}}\]
\[\Rightarrow x=2a+a{{t}^{2}}\]
So , the point of intersection of the axis and the normal is \[\left( 2a+a{{t}^{2}},0 \right)\].
Now , let the midpoint of intercepted portion be \[\left( h,k \right).....\left( iii \right)\]
But we also know that the extremities of the intercepted portion are \[\left( a{{t}^{2}},2at \right)\] and \[\left( 2a+a{{t}^{2}},0 \right)\].
Now, we know that the coordinates of the midpoint of the line joining two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given as: \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
So, the coordinates of the midpoint are
\[\left( \dfrac{a{{t}^{2}}+2a+a{{t}^{2}}}{2},\dfrac{2at+0}{2} \right)\]
\[=\left( a{{t}^{2}}+a,at \right)...\left( iv \right)\]
So, from \[\left( iii \right)\]and \[\left( iv \right)\], we can say
\[h=a{{t}^{2}}+a....\left( v \right)\], \[k=at\]
Now, \[k=at\]\[\Rightarrow t=\dfrac{k}{a}...\left( vi \right)\]
Substituting \[t=\dfrac{k}{a}\]in \[\left( v \right)\], we get
\[h=a{{\left( \dfrac{k}{a} \right)}^{2}}+a\]
\[\Rightarrow h=\dfrac{{{k}^{2}}}{a}+a\]
\[\Rightarrow {{k}^{2}}=ah-{{a}^{2}}........\] equation\[(vii)\]
Now , to get the equation of the locus of \[\left( h,k \right)\], we will substitute \[(x,y)\] in place of \[\left( h,k \right)\] in equation\[(vii)\].
Or, \[{{y}^{2}}=a\left( x-a \right)....\left( viii \right)\] is the equation of the locus.
Now , we know the length of the latus rectum of \[{{y}^{2}}=4ax\] is \[4a\].
Now , the length of latus rectum of parabola given by equation \[\left( vii \right)\]is \[4\times \dfrac{a}{4}=a\]
Also, the vertex of \[\left( viii \right)\] is \[\left( a,0 \right)\] which is the focus of \[{{y}^{2}}=4ax\]
Hence , the length of the latus rectum of the locus is one quarter of the original parabola and the vertex of the locus is the focus of the original parabola .
Note: Length of latus rectum of parabola \[{{y}^{2}}=4ax\] is equal to \[4a\] and not \[a\].
Focus of parabola \[{{y}^{2}}=4ax\] is \[\left( a,0 \right)\] and not \[(4a,0)\].
Students generally get confused and make mistakes which results in wrong answers. So , such mistakes should be avoided .
First of all , let’s take the equation of the parabola to be \[{{y}^{2}}=4ax\].
Coordinates of any point on the parabola in parametric form is given as \[P\left( a{{t}^{2}},2at \right)\].
We know, equation of normal in parametric form , where the normal is drawn at a point \[P\] with parameter \[t\], is given as
\[y=-tx+2at+a{{t}^{3}}....\left( i \right)\]
Also, the equation of axis of the parabola is
\[y=0.....\left( ii \right)\]
To find the points of intersection of \[\left( i \right)\]and\[\left( ii \right)\], we substitute \[y=0\] in \[\left( i \right)\].
So, \[0=-tx+2at+{{t}^{3}}\]
\[\Rightarrow x=2a+a{{t}^{2}}\]
So , the point of intersection of the axis and the normal is \[\left( 2a+a{{t}^{2}},0 \right)\].
Now , let the midpoint of intercepted portion be \[\left( h,k \right).....\left( iii \right)\]
But we also know that the extremities of the intercepted portion are \[\left( a{{t}^{2}},2at \right)\] and \[\left( 2a+a{{t}^{2}},0 \right)\].
Now, we know that the coordinates of the midpoint of the line joining two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given as: \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
So, the coordinates of the midpoint are
\[\left( \dfrac{a{{t}^{2}}+2a+a{{t}^{2}}}{2},\dfrac{2at+0}{2} \right)\]
\[=\left( a{{t}^{2}}+a,at \right)...\left( iv \right)\]
So, from \[\left( iii \right)\]and \[\left( iv \right)\], we can say
\[h=a{{t}^{2}}+a....\left( v \right)\], \[k=at\]
Now, \[k=at\]\[\Rightarrow t=\dfrac{k}{a}...\left( vi \right)\]
Substituting \[t=\dfrac{k}{a}\]in \[\left( v \right)\], we get
\[h=a{{\left( \dfrac{k}{a} \right)}^{2}}+a\]
\[\Rightarrow h=\dfrac{{{k}^{2}}}{a}+a\]
\[\Rightarrow {{k}^{2}}=ah-{{a}^{2}}........\] equation\[(vii)\]
Now , to get the equation of the locus of \[\left( h,k \right)\], we will substitute \[(x,y)\] in place of \[\left( h,k \right)\] in equation\[(vii)\].
Or, \[{{y}^{2}}=a\left( x-a \right)....\left( viii \right)\] is the equation of the locus.
Now , we know the length of the latus rectum of \[{{y}^{2}}=4ax\] is \[4a\].
Now , the length of latus rectum of parabola given by equation \[\left( vii \right)\]is \[4\times \dfrac{a}{4}=a\]
Also, the vertex of \[\left( viii \right)\] is \[\left( a,0 \right)\] which is the focus of \[{{y}^{2}}=4ax\]
Hence , the length of the latus rectum of the locus is one quarter of the original parabola and the vertex of the locus is the focus of the original parabola .
Note: Length of latus rectum of parabola \[{{y}^{2}}=4ax\] is equal to \[4a\] and not \[a\].
Focus of parabola \[{{y}^{2}}=4ax\] is \[\left( a,0 \right)\] and not \[(4a,0)\].
Students generally get confused and make mistakes which results in wrong answers. So , such mistakes should be avoided .
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
.png)
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
JEE Main & Advanced 2023
-
-
NEET
-
NEET 2021
-
NEET 2022
-
NEET 2023
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Micro Courses
-
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
