Question

Let \[L\] denote the set of all straight lines in a plane. Let a relation \[R\] be defined by \[\alpha R\beta \Leftrightarrow \alpha \bot \beta \],\[\alpha ,\beta \in L\]. Then \[R\] is
A. Reflexive
B. Symmetric
C. Transitive
D. None of these

Answer 1

Hint: In this question, we are given a relation \[R\] which is defined as \[\alpha R\beta \Leftrightarrow \alpha \bot \beta \],\[\alpha ,\beta \in L\]. We have to tell about what is the relation \[R\], is reflexive or symmetric, or it is transitive or it is none of the mentioned properties. We will be using the definition and concept of reflexive, symmetric, and transitive to find out.

Complete step-by-step solution:
 From the definitions of reflexive, symmetric, and transitive, we get the following results
1. Reflexive: As per the reflexive property, if \[R\] is reflexive then each line in the set \[L\] must be perpendicular to itself but this is not possible i.e., it is not possible that a line is perpendicular to itself
Thus, \[R\] is not reflexive
2. Symmetric: As per the symmetric property, if \[R\] is symmetric then a line in the set \[L\] must be perpendicular to another line and so the other line would also be perpendicular to the previous line i.e.,
If \[\alpha \bot \beta \Leftrightarrow \beta \bot \alpha \] which is true for all the lines present in the set \[L\].
3. Transitive: As per the transitive property, if \[R\] is transitive, \[l,m,n\] are 3 lines in the set \[L\], if \[l \bot m\] and \[m \bot n\], then \[l \bot n\] but this is not true in all cases.
Consider following example where \[l \bot m\] and \[m \bot n\] but \[l,n\] are not perpendicular.

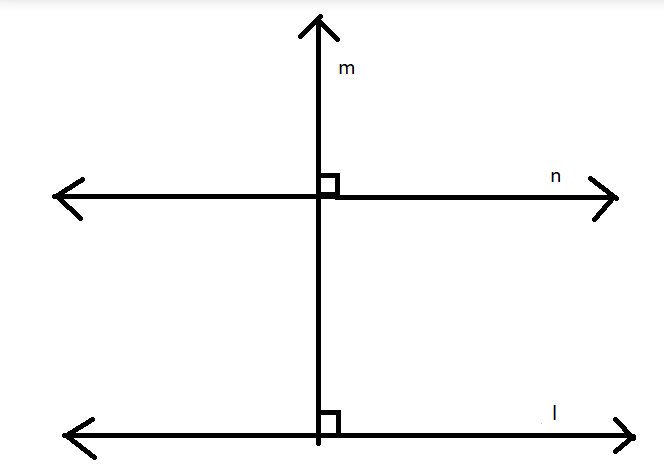
Image: figure shows 2 parallel lines \[l,n\] and \[m\] is perpendicular to \[l,n\].
So in all cases, if \[l \bot m\] and \[m \bot n\], then \[l \bot n\], this is not true.
Thus \[R\] is not transitive.

Hence, option (B) is correct

Note: While checking the transitive portion, the scholars might make the mistake of thinking of the matching axis with \[x\]-axis, \[y\]- axis, and \[z\]- axis in which all the axes are vertical to each other. But always flashback that to prove commodity is true, you have to give a perfect explanation not an illustration and to prove commodity wrong, we just need an illustration to do so.