Question

In the circuit shown figure, $R = \sqrt {\dfrac{L}{C}} $ the switch S is closed at time $t = 0$. The current through the capacitor and inductor will be equal at time $t$ equal to:

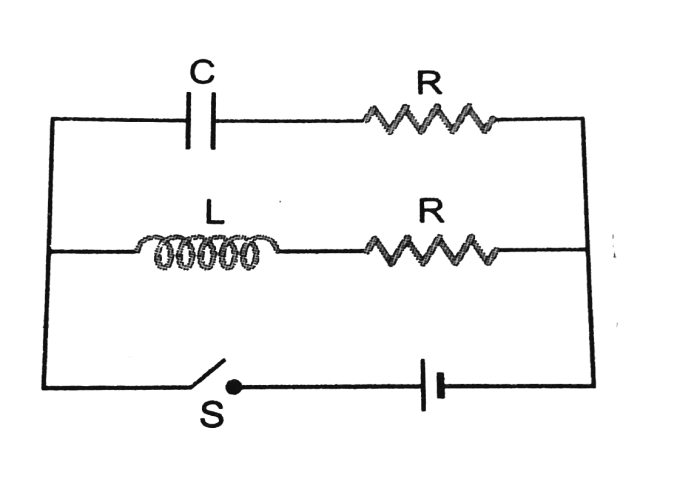
A) $CR$
B) $CR\log 2$
C) $\dfrac{L}{{R\log 2}}$
D) $LR$

Answer 1

Hint: A RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, associated in arrangement or in equal. A significant property of this circuit is its capacity to resonate at a particular frequency, the reverberation/resonance recurrence. Right now the impedances of the inductor and capacitor at reverberation are equivalent yet of inverse sign and counteract.

Complete step by step solution:
A RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, associated in series or in equal parallel. The circuit shapes a consonant oscillator for current, and resounds likewise as a LC circuit. Presenting the resistor expands the rot of these motions, which is otherwise called damping. The resistor additionally diminishes the pinnacle resounding recurrence.

A significant property of this circuit is its capacity to resonate at a particular frequency, the reverberation/resonance recurrence. Reverberation happens on the grounds that energy for this circumstance is put away in two unique manners: in an electric field as the capacitor is charged and in an attractive/magnetic field as flow courses through the inductor. The reverberation recurrence is characterized as the recurrence at which the impedance of the circuit is at least. Proportionately, it tends to be characterized as the recurrence at which the impedance is simply genuine (that is, absolutely resistive). This happens on the grounds that the impedances of the inductor and capacitor at reverberation are equivalent however of inverse sign and counterbalance.

$\therefore {I_C} = {I_L}$
As we know
${I_C}$ = $\dfrac{V}{R}e^{\dfrac{ - t}{RC}}$ and ${I_L}$ = ${\dfrac{V}{R}}({1 - e^{\dfrac{-Rt}{L}}})$
Insert these in above equation
$ \Rightarrow \dfrac{V}{R}e^{\dfrac{ - t}{RC}}$ = ${\dfrac{V}{R}}({1-e^{\dfrac{-Rt}{L}}})$ ……..(1)
But $R = \sqrt {\dfrac{L}{C}} $
$ \Rightarrow {R^2} = \dfrac{L}{C} \Rightarrow RC = \dfrac{L}{R}$
Put the values in equation in (1)
Collect like terms
$ \Rightarrow 2{{{e}}^{\dfrac{{{{ - t}}}}{{{{RC}}}}}}{{ = 1}}$
Therefore,
$ \Rightarrow {{{e}}^{\dfrac{{{{ - t}}}}{{{{RC}}}}}}{{ = }}\dfrac{1}{2}$
At last
$ \Rightarrow t = RC\log 2$

Hence option (B) is correct.

Note: A significant property of RLC circuit is its capacity to resonate at a particular frequency, the reverberation/resonance recurrence. Right now the impedances of the inductor and capacitor at reverberation are equivalent yet of inverse sign and counteract. So remember the above fact.
$ \Rightarrow {{{e}}^{\dfrac{{{{ - t}}}}{{{{RC}}}}}}{{ = 1 - }}{{{e}}^{\dfrac{{{t}}}{{RC}}}}.$